Eco-Drive Experiment on Rolling Terrain for Fuel Consumption Optimization

Chapter 3. Vehicle Control Formulation and Design

This section introduces the two speed controllers used in our experiment. The first is an upper-level controller that is responsible for trajectory planning to generate optimal speed profiles. The other is a secondary controller that adjusts speed commands in real time for enhanced performance and contains a classic proportional-integral-derivative (PID) controller for vehicle speed following. The recommended speed profiles generated from the upper-level controller will be filtered by the secondary controller and sent to the vehicle for execution.

UPPER-LEVEL CONTROLLER – TRAJECTORY PLANNING FOR OPTIMAL SPEED PROFILES

This section describes the formulation of the vehicle upper-level controller. The controller optimizes vehicle fuel efficiency, mobility, and comfort. The inputs for this controller are the vehicle’s current speed and location together with the future road’s altitude and dynamic speed limit. The output of this controller is an optimal acceleration/speed trajectory.

State Explanation

In this experiment, a system of one single vehicle is considered. The system’s state vector x is defined as a vector consisting of the distance from the trip origin and the vehicle’s instant speed, as seen in equation 1.

(1)

Where:

x₁(t) = the distance from the origin (m).

x₂(t) = the vehicle’s instant speed (m/s).

The state dynamics are defined in equation 2.

(2)

Where

u₁(t) = the controlled acceleration for the test vehicle.

Cost Function

The cost function J is defined in equation 3.

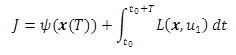
(3)

Where

ψ(x(T)) = terminal cost.

L(x,u₁) = running cost.

Equation 4 describes the terminal cost and equation 5 describes the running cost.

(4)

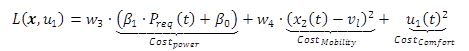
(5)

Where

w₁ and w₂ and = large positive numbers that are used to limit vehicle’s final state.

w₃, w₄ = weighting factors, greater than 0, balancing mobility and fuel efficiency.

v₁ = the test road’s speed limit (m/s).

With the inclusion of w₁ and w₂, the final cost ψ(x(T)) serves as a constraint on vehicle mobility. Therefore, the optimized speed profile is the most fuel efficient among all vehicle trajectories that have the same mobility as vehicles traveling at the speed limit. Cost_Mobility, which is the squared difference between the desired speed profile and the speed limit, prevents the speed from deviating significantly from the speed limit. Cost_Comfort encourages minimal speed change for drivability.

Cost_power defines fuel consumption associated with a given vehicle power request P_req, as defined in equation 6.

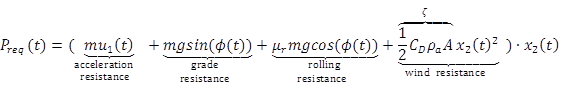
(6)

Where

m = mass of the vehicle.

g = gravity.

φ(t) = terrain slope (rad).

μ_r = rolling resistance coefficient.

C_D = drag coefficient.

ρ_a = density of air (kg/m³).

A = the vehicle frontal area (m²).

ζ = the constant describing drag (kg/m).

When positive, P_req represents the summation of power spent on vehicle state change. When negative, P_req describes the power dissipated by the brakes or, in the case of a hybrid or electric vehicle, used to charge the battery. The coefficients (β₀ and β₁) of the Cost_power model were acquired by fitting a linear equation representing power request against fuel consumption (Hu et al., 2016).

Vehicle Dynamic Model

The longitudinal vehicle dynamics model is shown in equation 7.

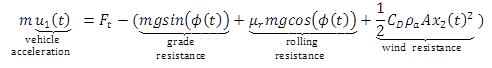
(7)

Where

F_t is the thrust force.

Constraints and Initial Conditions

Acceleration constraint: To ensure the feasibility of acceleration commands given the brake condition and engine maximum power constraints, the maximum acceleration is set as (F_max - F_R)/m m/s², and maximum deceleration is set as -5 m/s². F_max is the maximum thrust force of the powertrain and F_R is the summation of the three resistant forces (see equation 7). Note that this acceleration constraint is solely for the eco-drive controller. When a safety hazard arises, collision prevention applications can overrule this constraint and provide much greater deceleration. This constraint can be expressed as a permissible set of acceleration, shown in equation 8.

(8)

Speed constraint: Due to safety considerations, the speed change range is predetermined. In this study, maximum speed is 4.48 m/s (10 mph) above the speed limit and minimum speed is 4.48 m/s (10 mph) below the speed limit. This constraint is specified in equation 9.

(9)

Vehicle dynamic constraints: The dynamics of the vehicle should follow the laws of physics, specifically those defined in equation 2.

The initial conditions are shown in equations 10 and 11.

(10)

(11)

Solution Based on Pontryagin’s Minimum Principle (PMP)

In general, PMP entails defining the Hamiltonian H as shown in equation 12.

(12)

Where

λ = the gradient of the total cost-to-go of the state x.

In other words, λ is the extra cost of J caused by a small change ∂x on the state x. λ is also known as the co-state. According to PMP, for all control values that fall within the parameters of permissible controls set U, the optimal control u* must satisfy the requirements in equation 13.

(13)

The above Hamiltonian law could be expressed alternatively as the necessary conditions in equation 14.

(14)

Equation 14(iii) is equivalent to the vehicle dynamics. Equations 14(i) and 14(ii) serve to solve for optimal control. For vehicle-level optimization, substitute Hamiltonian H with the cost function of this study, shown in equation 15.

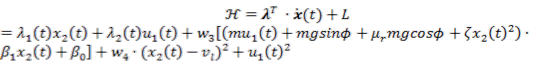
(15)

Applying the condition in equation 14(i) to the cost function gives equation 16.

(16)

Equation 16 can be rearranged to provide the control law in equation 17.

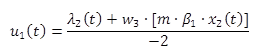
(17)

Applying the condition in equation 14(ii) to the cost function gives equations 18 and 19.

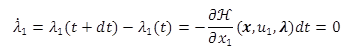
(18)

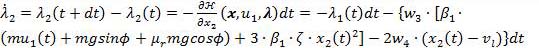
(19)

To enforce the desired final state x(t₀ + T) to ensure the mobility of the optimized vehicle, the final condition for λ (defined in equation 20) needs to be met.

(20)

Expanding equation 20 gives equations 21 and 22.

(21)

(22)

Iterative PMP Solving Process

To solve the aforementioned problem for optimal vehicle speed control, a numerical solution is adopted here (Hoogendoorn et al., 2012). The main idea is to find state x in a forward pass (utilizing the λ from the previous iteration) and then find λ in a backward pass. The procedure is summarized in the following:

1. Assume the initial state of co-state Λ⁽⁰⁾(t) = 0 for t ∈[t_i,t_i+1].
2. Start the iteration loop.
3. Solve the state dynamic equations forward in time for x⁽ⁿ⁾(t) using Λ^(n-1) computed from the previous iteration. All constraints apply. Altitude and speed limit are updated according to the vehicle’s actual speed and position.
4. Solve for the co-state λ⁽ⁿ⁾(t) backward in time utilizing x⁽ⁿ⁾(t) from the previous step.
5. Update the co-state Λ⁽ⁿ⁾, given in equation 23, based on the co-state λ⁽ⁿ⁾(t) and the prior co-state Λ^(n-1) from the previous iteration. Λ is a weighting factor that smooth the co-state updating process.

(23)

6. Check for error magnitude. Stop the iteration until ‖Λ⁽ⁿ⁾ − λ⁽ⁿ⁾‖ < ∈_max, otherwise loop back to step 3. ∈_max is a preset error tolerance level.

SECONDARY SPEED CONTROLLER

The optimal trajectory obtained from the last section will be converted to a recommended speed profile and input into the vehicle secondary speed controller, as illustrated in figure 2. The vehicle secondary speed controller contains three main components: brake reduction, speed limit, and PID control.

Source: FHWA
Figure 2. Vehicle secondary speed controller diagram.

Brake Reduction

It is very difficult for vehicles to precisely follow the recommended optimal speed profile, and thus it occurs quite frequently that the recommended speed is slightly less than the current speed. If no additional control logic is added, vehicles may brake frequently when going downhill, and this wastes a lot of the energy that should be transferred to kinetic energy as the speed increases. Some testing results even show negative benefits compared with cruise control because of the frequent braking. Therefore, additional control logic is included in figure 2 such that when the recommended speed is higher than the current actual speed, the actual speed is used as the updated speed command. This is implemented by limiting the error term that is used by the PID controller to only positive values.

Speed Limit

The reduction in braking may also lead to higher vehicle speeds. To reduce the possibility of unsafe speeds, the speed limit component restricts the maximum speed by a preset overage. This value can be any value as long as safe vehicle operation is guaranteed. In the case shown in figure 2, the allowed overage was set to 5 mph. Permitting a tolerant value above the speed limit may increase the benefits of eco-drive because it allows for the full transformation between potential and kinetic energy while maintaining an acceptable safety margin. The possibility of increased benefits is also based on the assumption that an automated vehicle has a shorter reaction time, and thus is able to travel faster. This limit on speed is implemented by allowing negative values for the error term that is used by the PID controller, but only if those values are more than the allowed overage below zero.

PID Control

Initial testing revealed that a badly tuned PID controller is detrimental to eco-drive effectiveness, and even consumes more fuel than cruise control in some cases. This is because poorly tuned PID parameters may cause frequent acceleration and deceleration as the controller attempts to drive the vehicle at the target speed. Energy is wasted while braking and more fuel is wasted during accelerations.

The parameters to be tuned are the proportional, integral, and derivative gains set in the Simulink PID block. The PID controller uses an error term that is the difference between the actual vehicle speed and the desired vehicle speed. The PID gains—k_P, k_I, and k_D—are applied within the PID control block and a wrench effort command is generated. This command is applied to the lower-level vehicle controller. The wrench effort is a percentage between -100 and +100, where -100 to 0 percent loosely relates to braking in the range of -2.5 to 0 m/s² and 0 to +100 percent loosely relates to acceleration in the range of 0 to 2.5 m/s².

To estimate the PID gains, a Simulink model is constructed and used to develop an initial set of values. Further PID tuning is performed through a manual tuning process during the field experiment. The first step is to gradually increase k_P until an oscillation is observed in the output, then this value of k_P is halved. Next, k_I is increased enough to minimize the steady-state output error. Finally, k_D is increased until the step response of the loop is acceptable. These parameters are usually particular to the dynamics of the experimental vehicle system, and different studies need to tune their own PID gains because of different vehicular dynamics.

In a PID controller with nonzero k_I, errors can accumulate while the PID controller is inactive, but the error signal is nonzero. This integrator windup is eliminated with an enable signal that is applied to the PID block. While the vehicle controller is inactive, the PID block is disabled and the output remains at zero. When the vehicle controller is activated, the PID operates normally.

During the field experiment, each speed command is associated with a GPS coordinate and corresponding circular geofence along the roadway. The vehicle PC constantly checks to see if the current location is within a geofence. If so, the vehicle will execute the new speed command. If not, the vehicle will keep following the last speed command. The interval between these commands and the size of the geofence need to be predetermined. Also, there is delay between the time when GPS data are received by the antenna and the time when the vehicle finishes executing the speed command (including vehicle response delay). It is necessary to account for this delay by advancing the time at which commands are sent to the vehicle. The question is how far in advance a speed command should be given to the vehicle such that the vehicle’s speed can be close to the optimal speed (i.e. speed command) when arriving at certain location. Another parameter that needs to be determined is maximum acceleration (a required input for the vehicle control system). Initial experiments were conducted, and multiple scenarios with combinations of these parameters were tested.