U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-13-077 Date: January 2014 |
Publication Number: FHWA-HRT-13-077 Date: January 2014 |
This chapter reviews the existing state of knowledge about the safety effects of horizontal curves and grades prior to the current research.
Design criteria for horizontal and vertical alignment are presented in chapter 3 of the AASHTO Policy on Geometric Design of Highways and Streets, commonly known as the Green Book.(2) Many State highway agencies have their own design manuals, but they tend to closely resemble the AASHTO Green Book in the areas of horizontal and vertical alignment.(2)
The key design parameters for horizontal curves include the following:
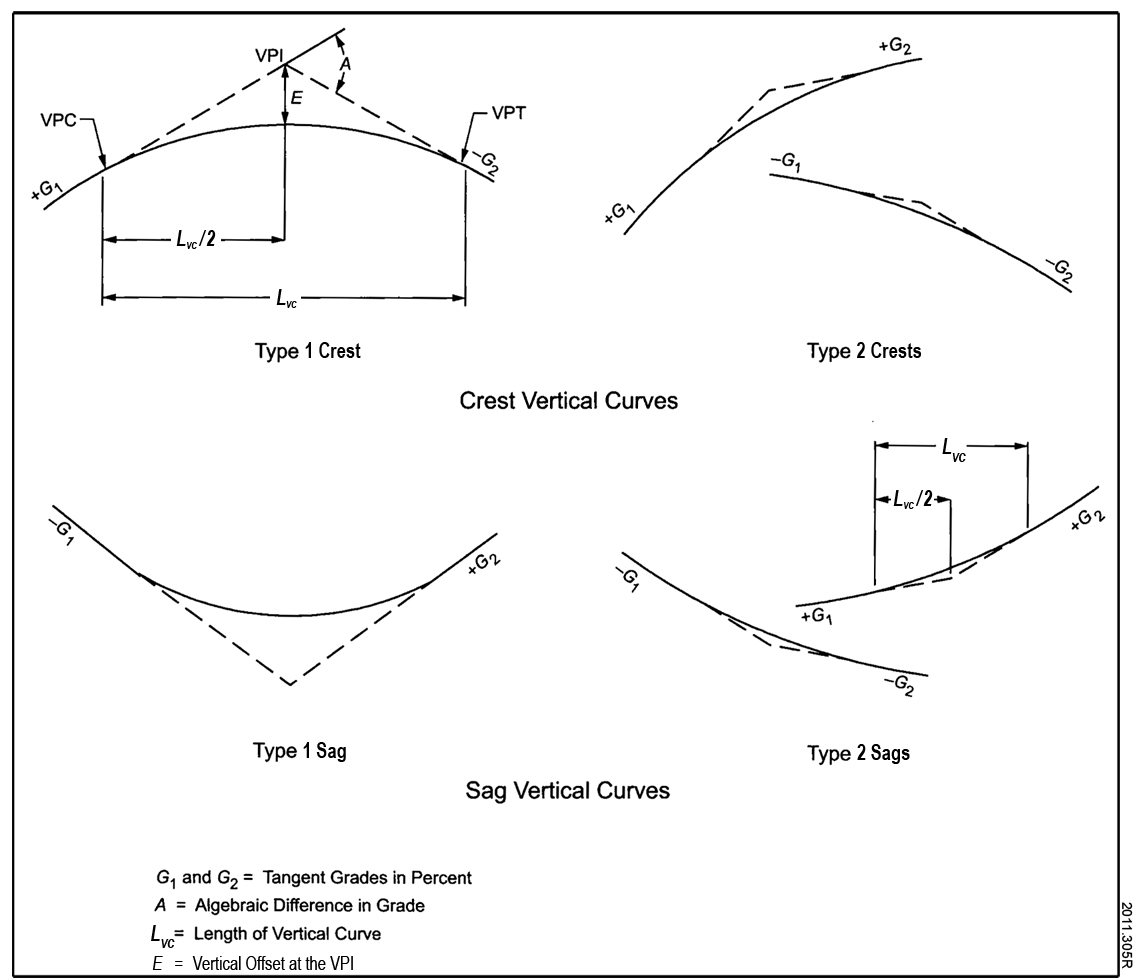
The fundamental design parameter for vertical alignment is the percent grade, which is defined as 100 times the change in roadway elevation per unit length of roadway measured in the horizontal plane. A road section with constant percent grade, regardless of its horizontal alignment, is generally referred to as a straight grade. Where the grade of the roadway changes, the straight grade sections are normally joined by a parabolic vertical curve. Figure 1 illustrates the four types of vertical curves (two types of crest vertical curves and two types of sag vertical curves) that are used in highway design. Key design parameters for vertical curves include the following:
 |
| Source: AASHTO. Used by permission. |
Figure 1. Illustration. Types of vertical curves.(2)
The most widely used safety relationship for horizontal curves on rural two-lane highways was developed by Zegeer et al. in the early 1990s as follows shown in figure 2*:(3,4)
*Modified on November 16, 2014
![]()
![]()
Figure 2. Equation. Relationship between crash rates and curve characteristics.
*Modified on November 16, 2014
Where:
N = Total number of crashes on curve per year.
LC = Length of curve (mi).
V = Volume of vehicles (in millions) passing through the curve in a 1 year period.
D = Degree of curvature (5,730/radius of curvature (ft)).
S = Presence of spiral transitions, where S = 0 if no spirals exist and S = 1 if spirals do exist.
W = Width of roadway on curve (ft).
D, which represents the deflection angle for the curve per 100 ft of curve length, is an obsolete measure that is no longer used in the AASHTO Green Book.(2) Therefore, the equivalent to degree of curvature expressed in terms of the radius of curvature is provided. The original Zegeer et al. model was expressed in terms of predicting crash frequency for a 5 year period; the model in figure 2 is expressed on a per-year basis for ease of comparison to other models.
No safety relationships for horizontal curvature have been developed for highway types other than rural two-lane highways, although such relationships for freeways have been developed in National Cooperative Highway Research Program Project 17 45.(5)
An assessment of literature conducted by Harwood, et al., as part of the development of the FHWA Interactive Highway Safety Design Model, concluded that the Zegeer, et al. model in figure 2 was the most useful and accurate model to account for the safety effect of horizontal curves on rural two-lane highways.(6,7) Harwood et al. expressed the Zegeer, et al. model as a CMF in the following form shown in figure 3*:(6)
*Modified on November 16, 2014
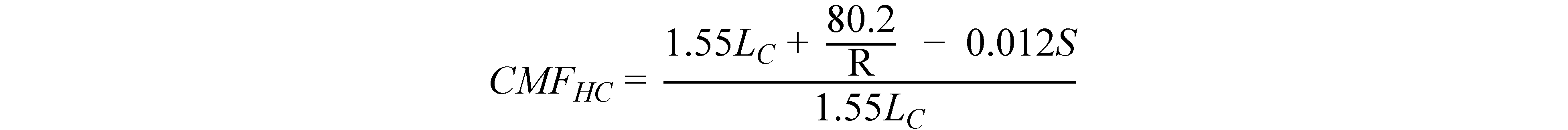
Figure 3. Equation. CMF for horizontal curves on rural two-lane highways.
Where:CMFHC = CMF for horizontal curvature on a rural two-lane highway.
R = Radius of curvature (ft).
The base condition for this CMF is a tangent roadway. The AASHTO HSM adopted the CMF in figure 3 to represent the safety effects of horizontal curvature on rural two-lane highways.(1)
The AASHTO HSM also includes a CMF for the safety effect of superelevation for horizontal curves of rural two-lane highways as a function of superelevation variance in the following form as shown in figure 4:*
*Modified on November 16, 2014
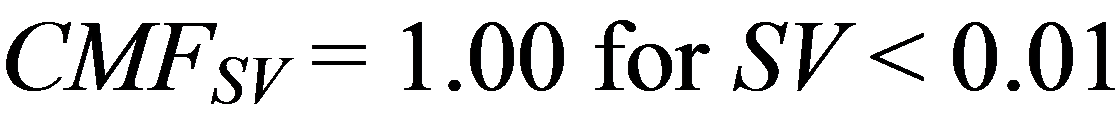 |
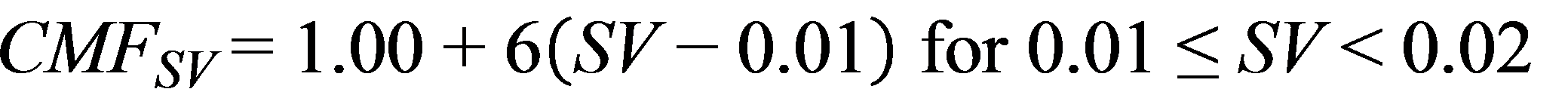 |
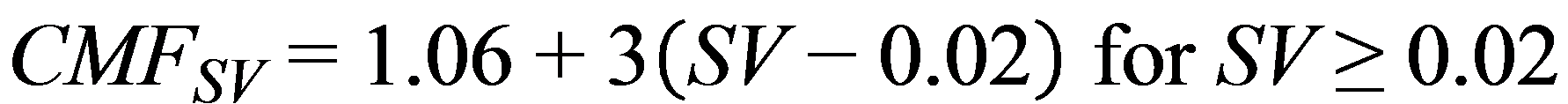 |
Figure 4. Equation. CMF for superelevation as a function of superelevation variance.
Where:
CMFSV = CMF for superelevation variance on a rural two-lane highway.
SV = Superelevation variance (ft/ft), which represents the design superelevation rate presented in the AASHTO Green Book minus the actual superelevation of the curve.(2)
CMF was also adapted by Harwood et al. from the work of Zegeer et al.(3,4,6) The base condition for CMF is a horizontal curve with superelevation within 0.01 ft/ft of the applicable design superelevation presented in the AASHTO Green Book.(2)
No CMFs for horizontal curvature on rural multilane undivided highways, rural multilane divided highways, or urban and suburban arterials are included in the AASHTO HSM.(1)
Table 1 presents the AASHTO HSM CMF, denoted as CMF5r, which represents the safety effect of percent grade on rural two-lane highways.
Table 1. CMF for grade of roadway segments.(1)
Level Grade |
Moderate Terrain |
Steep Terrain |
1.00 |
1.10 |
1.16 |
The base condition for the CMFs shown in table 1 is a level roadway. Figure 5 represents the underlying functional form for CMF shown in table 1.
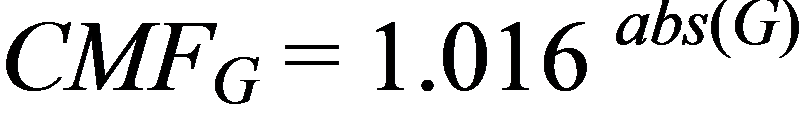
Figure 5. Equation. CMF for percent grade on rural two-lane highways.
CMFG = CMF for percent grade on a rural two-lane highway.
abs(G) = Absolute value of percent grade.
The CMF in this form, as a continuous function, is a more useful representation of the safety effect of percent grade than the form shown in table 1, as the stepwise function in table 1 may be misleading.
The CMF for percent grade shown in table 1 and figure 5 applies only to straight grades. There are no CMFs in the AASHTO HSM for crest or sag vertical curves on rural two-lane highways. Also, there are no vertical alignment CMFs in the AASHTO HSM for facility types other than rural two-lane highways.
While the AASHTO HSM provides CMFs for the safety effects of horizontal curvature and percent grade on rural two-lane highways, it does not have any method for accounting for the interactions between these effects. In other words, in the AASHTO HSM procedures for rural two-lane highways, the safety effect of a horizontal curve is the same whether it is located on a level roadway, a straight grade, or a vertical curve. Similarly, the safety effect of a straight grade is the same whether it is located on a tangent roadway or on a horizontal curve. Researchers have always assumed that there are interactions between the safety effects of horizontal and vertical alignment, but this has not been demonstrated in a form useful for safety prediction. Recent research by Easa and You have partially addressed this issue with separate models for horizontal curves and horizontal tangents, but they did not tie their models back to a common base condition (such as a level tangent roadway) or express the modeling results in a form that could be considered a CMF.(8,9)