U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-13-077 Date: January 2014 |
Publication Number: FHWA-HRT-13-077 Date: January 2014 |
The overall statistical approach to estimating the safety effects of horizontal curve and grade combinations on rural two-lane highways is presented in this chapter along with the results for each type of combination for FI and PDO crashes.
The safety effects of horizontal curve and grade combinations are estimated based on a cross-sectional analysis using a generalized linear model approach assuming a negative binomial (NB) distribution of crash counts and an exponential model using the combined crash data from all 6 years and selected roadway geometrics. FI and PDO crashes were modeled separately for each of the five types of horizontal curve and grade combinations.
Selection of Independent Variables Considered in Models
The parameters considered in each model may include the following:
For each type of horizontal curve and grade combination, the dataset used for modeling included the roadway segments for the relevant curve and grade combination but also all level tangents (i.e., no horizontal curvature and grade < 1 percent) to serve as the base condition.
Modeling was performed by encoding each parameter, or a transformation of it, so as to treat roadway segments on horizontal curve and grade combinations separately from tangent roadways on nonlevel grades and from level tangents (base condition). Segments for all of these types were used to develop a single model. This is equivalent to using indicator variables for each type of roadway segment. For example, since the natural log of the inverse radius was used in some of the models, the radius was recoded as ln(2 × ![]() ) based on the following reasoning:
) based on the following reasoning:
the smallest value of ![]() for horizontal curves in the database is 0.5. Therefore, the ratio,
for horizontal curves in the database is 0.5. Therefore, the ratio, ![]() , was multiplied by 2 such that the smallest value of ln(2 ×
, was multiplied by 2 such that the smallest value of ln(2 × ![]() ) becomes zero. This term was then set equal to zero for all tangents. This approach ultimately allows for the computation of CMFs using the developed models (discussed in further detail in chapter 5 of this report).
) becomes zero. This term was then set equal to zero for all tangents. This approach ultimately allows for the computation of CMFs using the developed models (discussed in further detail in chapter 5 of this report).
Within each vertical alignment type (i.e., straight grades, type 1 crest vertical curves, type 1 sag vertical curves, type 2 crest vertical curves, and type 2 sag vertical curves), the functional form of the relationship between crash frequency (FI or PDO) and the parameters listed was assessed separately. The following approach was used to explore the appropriate functional form for these relationships:
*Modified on November 16, 2014
Based on the visual assessment of these relationships, a final model form was selected using all parameters and relevant interactions. The parameters in these final model forms were continuous variables. In other words, the categorization into three groups was used only for exploring the potential functional forms for the data and was not used in the final models.
Before analyzing crashes on horizontal curves, tangents on nonlevel grades, and level tangents using a single model, the effect of vertical curve characteristics was assessed using tangents alone. This was done by comparing the effect of vertical curve characteristics on crashes/mi/year between level tangents and tangents on nonlevel grades for each type of vertical curve. This subset of data represents the largest proportion of the database. If a vertical curve parameter showed a statistically significant effect for tangents on nonlevel grades, then that parameter was included as such in the model using all three types of roadway (horizontal curves, level tangents, and tangents on nonlevel grades).
An attempt was also made to model crashes on horizontal curves and tangents by allowing separate intercepts and AADT slopes (i.e., an analysis of covariance) for each segment type to assess whether the relationship between crash frequency and AADT differs among horizontal curves, tangents on nonlevel grades, and base condition tangents. This modeling effort was inconclusive (e.g., slopes were inconsistent and counterintuitive) and therefore abandoned.
Final crash prediction models were derived for horizontal curves and tangents using the same group of level tangent sections as the base condition for all five horizontal curve and grade combinations. A stepwise approach was used where all parameters and interactions were included. The least significant interaction(s) and then the least significant parameter(s) were eliminated one at a time until all remaining interactions and parameters were significant. This is known as backwards stepwise selection. At each step, extreme data points were excluded from the data using leverage estimates, residuals, or Cook´s D criterion, all statistical criteria to evaluate the goodness-of-fit of the model to the data. In general, a 5 percent significance level associated with the type 3 chi-squared statistic was selected. All analyses were performed using a procedure for fitting generalized linear models of SAS® Version 9.3.(10)
It should be noted that additional geometric features for roadway segments, such as lane and shoulder widths, were not included in the analysis. The decision to exclude other geometric features was made because they were outside the scope of the current research. Experience with the Zegeer et al. results found that the roadway width term was dropped out of the final CMF.(3,4,6) Also, it was unlikely that the available data would support inclusion of additional terms.
Once a model for a specific horizontal and vertical alignment combination was finalized, its goodness-of-fit to the observed crash data was evaluated. For each alignment combination and severity level, predicted crash frequencies versus observed frequencies were plotted and assessed to determine how well the data followed the line of equality. However, it should be recognized that perfect or near perfect agreement between predicted and observed crash frequencies should not be expected no matter how good the methodology is. The predicted crash frequencies, at their best, represent an estimate of the long-term average crash frequency for similar roadway segments. The observed crash frequency is simply one observation from a random process whose mean is estimated by the predicted crash frequency. There is no reason to expect that one observation from a random process should exactly equal the long-term mean. In addition, the methodology cannot predict a crash frequency of zero because each model has a positive intercept. This is reasonable because no roadway segment can ever be expected to be crash-free in the long term. However, in any given time period, it is reasonable to expect that many roadway segments, particularly lower volume segments, will experience zero observed crashes.
To assess the goodness-of-fit of each model, the level of agreement between predicted and observed crash frequencies was estimated based on the percentage of extreme observations in the 6-year period at the 5 percent significance level. Consideration of the likelihood of extreme observed crash frequencies, either high or low, is a method that directly takes into account the parameters of the NB distribution (i.e., mean and dispersion) of crash frequencies at a particular type of roadway segment.
Let Oi denote the number of observed crashes of a given type (FI or PDO) on a roadway segment, i, during the 6-year period. The likelihood of observing Oi crashes in 6 years is then computed under the assumption that Oi is an observation from a NB distribution with mean and dispersion parameter k. The mean is the predicted number of crashes in the 6-year period calculated using the prediction model applicable for roadway segment i. The dispersion parameter is obtained when developing the final model.
The likelihood, pi, of observing Oi or fewer crashes at roadway segment i can then be written
as follows shown in figure 6 and figure 7*:
*Modified on November 16, 2014
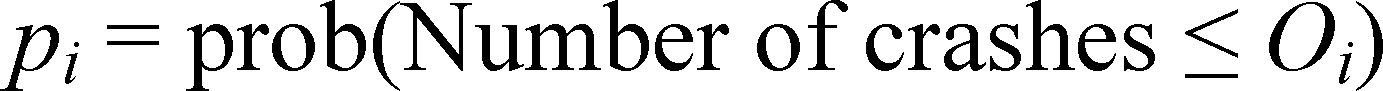
Figure 6. Equation. Probability of observing a given number of crashes.
Or:
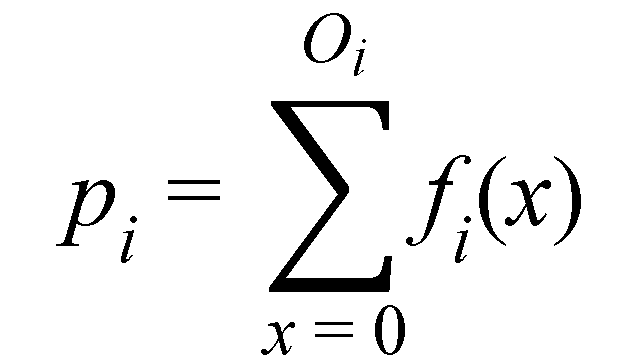
Figure 7. Equation. Probability of observing a given number of crashes expressed as a cumulative distribution.
Where fi(x) is the probability distribution function for an NB with μi and k and values of x = 0, 1, 2, …, Oi. If pi = 0.5, then pi was calculated as 1 - pi. This approach is equivalent to calculating the area under the cumulative distribution curve at either low or high tail of the distribution.
The following two final single-value criteria used to assess how well the observed crash frequencies can be estimated by the proposed methodology are proposed:
*Modified on November 16, 2014
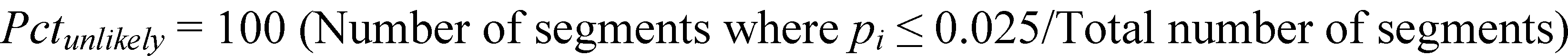
Figure 8. Equation. Percent of roadway segments with unlikely low or high crash numbers.
On average, the value of Pctunlikely would be close to 5 percent if the methodology is to fit the observed data reasonably well because one would expect that on average, 5 percent of the observed values be outside the middle 95 percent of the distribution. Such observed crash frequencies would be considered extreme (low or high) crash frequencies under the estimated distribution.This section presents the final modeling results for the five alignment categories for rural two-way highways. Each subsection is organized as follows:
For each alignment category considered, a level tangent roadway serves as the base condition.
Horizontal Curves and Tangents on Straight Grades
The following three alignment combinations shaded in figure 9 were included in the analysis:
*Modified on November 16, 2014
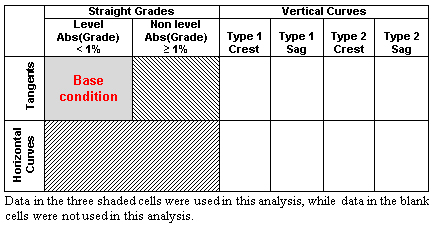
Figure 9. Illustration. Alignment combinations used in the analysis of horizontal curves and tangents on straight grades.
Basic descriptive statistics such as sample size (i.e., number of roadway sections); total roadway length; and minimum, maximum, mean, and median values for specific parameters) (i.e., number of roadway sections; total roadway length; and minimum, maximum, mean, and median values for specific parameters)* are shown in table 7 for each of the three alignment types included in the analysis.
*Modified on November 16, 2014
Table 7. Descriptive statistics for horizontal curves and tangents on straight grades.
Parameter |
Minimum |
Maximum |
Mean |
Median |
Horizontal Curves on Straight Grades |
||||
AADT (vehicles/day) |
169 |
26,088 |
2,695 |
1,664 |
Section length (mi) |
0.01 |
0.75 |
0.07 |
0.05 |
Horizontal curve length (mi) |
0.01 |
1.19 |
0.15 |
0.11 |
Curve radius (ft) |
100 |
11,459 |
2,067 |
1,433 |
Grade (percent) |
0 |
9.67 |
2.11 |
1.53 |
FI crashes per MVMT |
0 |
39.50 |
0.75 |
0 |
PDO crashes per MVMT |
0 |
46.26 |
0.91 |
0 |
Total crashes per MVMT |
0 |
54.62 |
1.66 |
0 |
Tangents on Nonlevel Grades |
||||
AADT (vehicles/day) |
169 |
26,088 |
2,700 |
1,644 |
Section length (mi) |
0.01 |
0.99 |
0.10 |
0.06 |
Horizontal curve length (mi) |
|
|
|
|
Curve radius (ft) |
|
|
|
|
Grade (percent) |
1.00 |
10.85 |
3.10 |
2.64 |
FI crashes per MVMT |
0 |
39.33 |
0.61 |
0 |
PDO crashes per MVMT |
0 |
44.14 |
0.80 |
0 |
Total crashes per MVMT |
0 |
53.48 |
1.42 |
0 |
Level Tangents—Base Condition |
||||
AADT (vehicles/day) |
169 |
26,088 |
3,285 |
2,153 |
Section length (mi) |
0.01 |
0.98 |
0.14 |
0.09 |
Horizontal curve length (mi) |
|
|
|
|
Curve radius (ft) |
|
|
|
|
Grade (percent) |
|
|
|
|
FI crashes per MVMT |
0 |
34.21 |
0.46 |
0 |
PDO crashes per MVMT |
0 |
39.50 |
0.67 |
0 |
Total crashes per MVMT |
0 |
55.38 |
1.13 |
0 |
Note: No roadway segments exist in the shaded cells.
The final crash prediction models for FI and PDO crashes are as follows shown in figure 10 and figure 11*:
*Modified on November 16, 2014
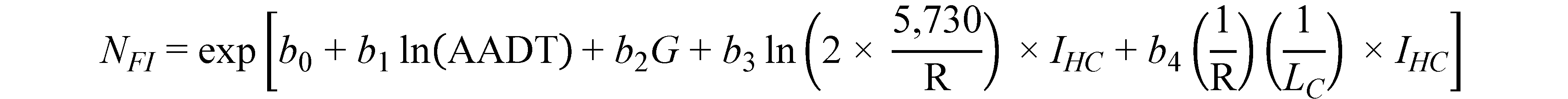
Figure 10. Equation. Predicted FI crashes on horizontal curves and tangents on straight grades (general form).
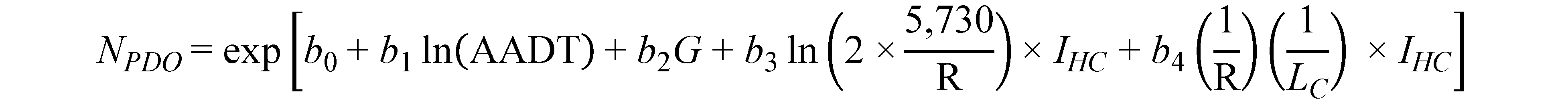
Figure 11. Equation. Predicted PDO crashes on horizontal curves and tangents on straight grades (general form).
Where:
NFI = FI crashes per mile per year.
NPDO = PDO crashes per mile per year.
AADT = Vehicles per day.
G = Absolute value of percent grade (0 percent for level tangents; ≥ 1 percent otherwise).
R = Curve radius (ft) (missing for tangents).
IHC = Horizontal curve indicator (1 for horizontal curves; 0 otherwise).IHC = Horizontal curve indicator (1 for horizontal curves; 0 otherwise).
LC = Horizontal curve length (mi) (not applicable for tangents).
ln = Natural logarithm function.
b0,…, b4 = Regression coefficients.
The regression results, including the coefficient estimate, dispersion parameter, standard error, confidence limit, chi-squared statistic, and significance level for all statistically significant parameters and interaction are shown in table 8.
Table 8. FI and PDO crash modeling results for horizontal curves and tangents on straight grades.
Parameter |
Regression |
Coefficient |
Standard |
Lower |
Upper |
Chi- |
Significance |
FI Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-8.76 |
0.15 |
-9.05 |
-8.46 |
N/A |
N/A |
ln(AADT) |
b1 |
1.00 |
0.02 |
0.96 |
1.03 |
3,052.7 |
< 0.0001 |
Grade |
b2 |
0.044 |
0.01 |
0.03 |
0.06 |
27.5 |
< 0.0001 |
1/radius terma |
b3 |
0.19 |
0.02 |
0.16 |
0.22 |
116.3 |
< 0.0001 |
1/R × 1/LC interaction |
b4 |
4.52 |
0.79 |
2.97 |
6.07 |
26.8 |
< 0.0001 |
Dispersion |
N/A |
0.85 |
0.04 |
0.77 |
0.94 |
N/A |
N/A |
PDO Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-8.63 |
0.14 |
-8.89 |
-8.36 |
N/A |
N/A |
ln(AADT) |
b1 |
1.03 |
0.02 |
1.00 |
1.06 |
4,003.5 |
< 0.0001 |
Grade |
b2 |
0.040 |
0.01 |
0.03 |
0.05 |
29.1 |
< 0.0001 |
1/radius terma |
b3 |
0.13 |
0.02 |
0.10 |
0.16 |
67.4 |
< 0.0001 |
1/R × I/LC interaction |
b4 |
3.80 |
0.84 |
2.15 |
5.45 |
17.3 |
< 0.0001 |
Dispersion |
N/A |
0.80 |
0.03 |
0.73 |
0.87 |
N/A |
N/A |
Applying figure 8, the percentage of roadway segments with extremely high observed FI crash frequencies was 6.09 percent across all roadway segments, which was only slightly above the expected 5 percent. The percentages were 6.12 percent for segments on level tangents, 6.25 percent for segments on tangents on nonlevel grades, and 5.91 percent for segments on horizontal curves on straight grades, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
Similarly, the percentage of roadway segments with extremely high observed PDO crash frequencies was 6.56 percent across all roadway segments, which was slightly higher than that for FI crashes. The percentages were 6.71 percent for segments on level tangents, 6.90 percent for segments on tangents on nonlevel grades, and 6.14 percent for segments on horizontal curves on straight grades, indicating that a few roadway segments in these roadway categories experienced unusually high PDO crash frequencies given the prediction model used. None of the segments experienced extremely low PDO crash frequencies under the assumed model at the 5 percent significance level.
The average probability of predicting a more extreme than observed FI crash frequency was calculated using figure 7. Across all roadway segments, the average probability was 0.13. The average probability was 0.14 for segments on level tangents, 0.11 for segments on tangents on nonlevel grades, and 0.13 for segments on horizontal curves on straight grades, all considerably lower than the theoretically expected value of 0.25.
Similarly, the average probability of predicting a more extreme than observed PDO crash frequency was 0.14 across all roadway segments. The average probability was 0.16 for segments on level tangents, 0.13 for segments on tangents on nonlevel grades, and 0.15 for segments on horizontal curves on straight grades, all considerably lower than the theoretically expected value of 0.25. For both FI and PDO crashes, these low probabilities are an indication that the model might not provide an adequate fit to the data. This is not too surprising given the large number of roadway segments with a wide range of AADTs and geometrics and a high percentage of segments with zero crashes.
Substituting the regression coefficients in figure 10 and figure 11 with their corresponding estimates in table 8, the prediction models for FI and PDO crashes/mi/year are as follows shown in figure 12, figure 13, and figure 14*:
*Modified on November 16, 2014
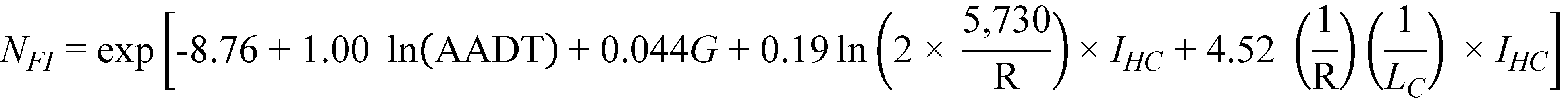
Figure 12. Equation. Predicted FI crashes on horizontal curves and tangents on straight grades (explicit form).
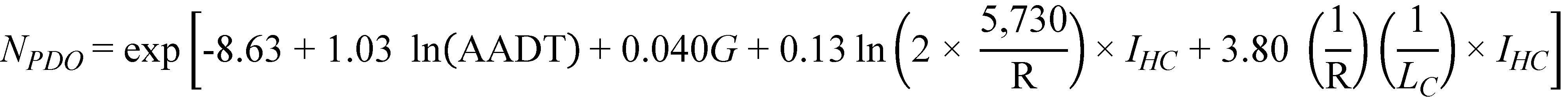
Figure 13. Equation. Predicted PDO crashes on horizontal curves and tangents on straight grades (explicit form).
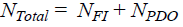
Figure 14. Equation. Predicted total crashes on horizontal curves and tangents on straight grades (general form).
Table 8 clearly shows that AADT is the most predominant predictor of crashes as indicated by its high chi-squared statistic. Other parameters and interaction are one or two orders of magnitude smaller and indicate that once the variability due to traffic volume is accounted for, the remaining parameters explain only a small portion of the remaining variability in the data. This is a consistent trait across all models developed in this project.
These final models include only two significant parameters and an interaction from the list of parameters and interactions originally considered. This is in large part because all safety effects are estimated relative to level tangents as the base condition. Crash frequencies in this group of roadway segments alone (5,701 segments for a total of 779 mi) exhibit considerable variability (e.g., FI crash rates range from zero to 34.21 with a mean of 0.46 and a median of zero crashes per MVMT as shown in table 7). To detect a significant effect of any horizontal curve characteristic on straight grades, the effect of such a characteristic would need to be large relative to the variability in the base condition set. This, in effect, is the challenge in finding statistically significant safety effects of practical engineering relevance.
Figure 12 and figure 13 show that crash frequency increases with increasing percent grade and decreases with increasing curve radius, as expected. The interaction term between radius and curve length represents an additional effect on safety for short and sharp horizontal curves—as the radius decreases and the curve shortens, the last term in figure 12 and figure 13 increases, adding to the crash frequency. For long horizontal curves and curves with larger radii, this term approaches zero and thus will have little impact on the predicted crash frequency.
Of interest is the fact that the effects of percent grade, curve radius, and the interaction between radius and curve length is more pronounced for FI crashes than for PDO crashes.
Initial modeling effects indicated that there might be an interaction between horizontal curve radius and percent grade on straight grade segments, suggesting that the effect of curve radius on crash frequency might change with increasing percent grade. However, this effect was found to be an artifact of a few data points that were clearly outliers. These outliers were eliminated from the dataset used to produce the final models presented in figure 12 and figure 13. Thus, the analysis did not find a statistically significant interaction between horizontal curve radius and percent grade. The results of the study presented in this report are as follows:
Horizontal Curves and Tangents at Type 1 Crest Vertical Curves
The following three alignment combinations shaded in figure 15 were included in the analysis:
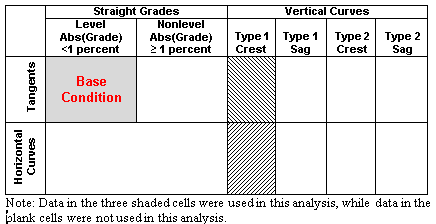
Figure 15. Illustration. Alignment combinations used in the analysis of horizontal curves and tangents at type 1 crest vertical curves.
Basic descriptive statistics such as sample size (i.e., number of roadway sections); total roadway length; and minimum, maximum, mean, and median values for specific parameters are shown in table 9 for each of the three alignment types included in the analysis.
Table 9. Descriptive statistics for horizontal curves and tangents at type 1 crest vertical curves.
Parameter |
Minimum |
Maximum |
Mean |
Median |
Horizontal Curves at Type 1 Crest Vertical Curves |
||||
AADT (vehicles/day) |
175 |
26,088 |
3,059 |
1,877 |
Section length (mi) |
0.01 |
0.72 |
0.07 |
0.06 |
Horizontal curve length (mi) |
0.02 |
1.00 |
0.16 |
0.12 |
Curve radius (ft) |
100 |
11,459 |
2,102 |
1,433 |
Vertical curve length (ft) |
100 |
4,000 |
824 |
600 |
A |
1.0 |
14.7 |
5.2 |
4.9 |
K |
11.1 |
985.2 |
186.2 |
147.9 |
FI crashes per MVMT |
0 |
23.10 |
0.55 |
0 |
PDO crashes per MVMT |
0 |
28.12 |
0.66 |
0 |
Total crashes per MVMT |
0 |
28.12 |
1.21 |
0 |
Tangents at Type 1 Crest Vertical Curves |
||||
AADT (vehicles/day) |
169 |
26,088 |
3,105 |
1,858 |
Section length (mi) |
0.01 |
0.59 |
0.10 |
0.08 |
Horizontal curve length (mi) |
|
|
|
|
Curve radius (ft) |
|
|
|
|
Vertical curve length (ft) |
60 |
4,000 |
776 |
600 |
A |
1.0 |
14.7 |
4.7 |
4.3 |
K |
5.4 |
985.2 |
192.4 |
151.5 |
FI crashes per MVMT |
0 |
20.85 |
0.40 |
0 |
PDO crashes per MVMT |
0 |
25.43 |
0.57 |
0 |
Total crashes per MVMT |
0 |
33.85 |
0.98 |
0 |
Level Tangents—Base Condition |
||||
AADT (vehicles/day) |
169 |
26,088 |
3,287 |
2,160 |
Section length (mi) |
0.01 |
2.10 |
0.15 |
0.09 |
Horizontal curve length (mi) |
|
|
|
|
Curve radius (ft) |
|
|
|
|
Vertical curve length (ft) |
|
|
|
|
A |
|
|
|
|
K |
|
|
|
|
FI crashes per MVMT |
0 |
34.21 |
0.46 |
0 |
PDO crashes per MVMT |
0 |
39.50 |
0.67 |
0 |
Total crashes per MVMT |
0 |
39.50 |
1.13 |
0 |
Note: No roadway segments exist in the shaded cells.
The final crash prediction models for FI and PDO crashes are as follows shown in figure 16 and figure 17*:
*Modified on November 16, 2014
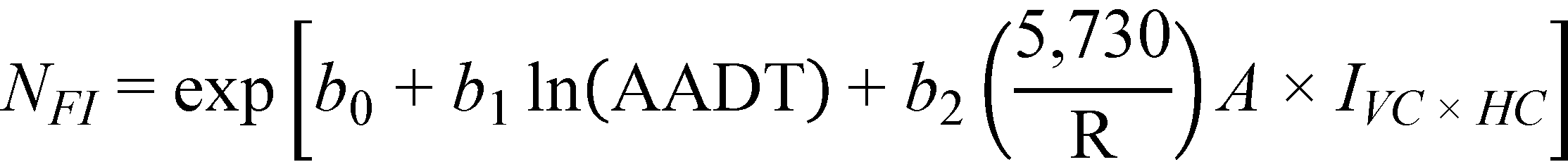
Figure 16. Equation. Predicted FI crashes on horizontal curves and tangents at type 1 crest vertical curves (general form).
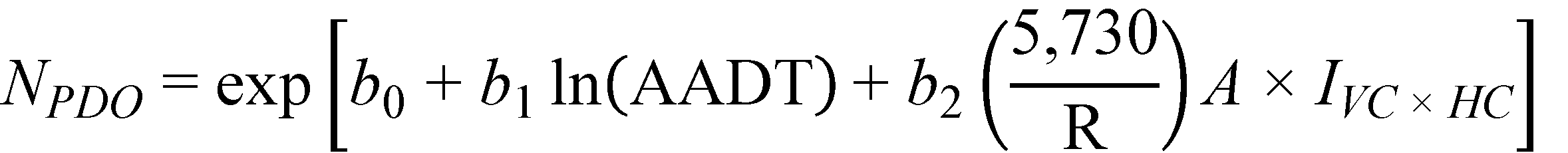
Figure 17. Equation. Predicted PDO crashes on horizontal curves and tangents at type 1 crest vertical curves (general form).
Where:
A = abs(G1 – G2) (percent); not applicable for level tangents.
G1 = Initial grade (percent) (positive for upgrade; negative for downgrade).
G2 = Final grade (percent) (positive for upgrade; negative for downgrade).
IVC × HC = Combined vertical and horizontal curve indicator (1 for combined vertical and horizontal curves; 0 otherwise).
The regression results, including the significant interaction, are shown in table 10.
Table 10. FI and PDO crash modeling results for horizontal curves and tangents at type 1 crest vertical curves.
Parameter |
Regression |
Coefficient |
Standard |
Lower |
Upper |
Chi- |
Significance |
FI Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-9.56 |
0.23 |
-10.01 |
-9.11 |
N/A |
N/A |
ln(AADT) |
b1 |
1.09 |
0.03 |
1.04 |
1.15 |
1,661.0 |
< 0.0001 |
1/R × A interactiona |
b2 |
0.0088 |
0.003 |
0.004 |
0.014 |
11.1 |
0.001 |
Dispersion |
N/A |
0.70 |
0.05 |
0.60 |
0.81 |
N/A |
N/A |
PDO Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-8.46 |
0.20 |
-8.85 |
-8.08 |
N/A |
N/A |
ln(AADT) |
b1 |
1.01 |
0.02 |
0.96 |
1.05 |
1,858.8 |
< 0.0001 |
1/R × A interactiona |
b2 |
0.0046 |
0.002 |
0.001 |
0.008 |
6.4 |
0.011 |
Dispersion |
N/A |
0.72 |
0.04 |
0.64 |
0.82 |
N/A |
N/A |
Using figure 8, the percentage of roadway segments with extremely high observed FI crash frequencies was 6.50 percent across all roadway segments, which was slightly above the expected 5 percent. The percentages of roadway segments with extremely high observed FI crash frequencies were 6.37 percent for level tangents, 6.52 percent for tangents at type 1 crests, and 7.08 percent for horizontal curves on type 1 crests, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
Similarly, the percentage of roadway segments with extremely high observed PDO crash frequencies was 6.70 percent across all roadway segments, similar to that for FI crashes. The percentages were 7.00 percent for level tangents, 5.94 percent for tangents at type 1 crests, and 6.59 percent for horizontal curves on type 1 crests, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
Similarly, the percentage of roadway segments with extremely high observed PDO crash frequencies was 6.70 percent across all roadway segments, similar to that for FI crashes. The percentages were 7.00 percent for level tangents, 5.94 percent for tangents at type 1 crests, and 6.59 percent for horizontal curves on type 1 crests, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
Similarly, the average probability of predicting a more extreme than observed PDO crash frequency was 0.15 across all roadway segments. The probability was 0.16 for level tangents, 0.14 for tangents on type 1 crests, and 0.13 for horizontal curves on type 1 crests, which are all considerably lower than the theoretically expected value of 0.25. For both FI and PDO crashes, these low probabilities indicate that the model might not provide an adequate fit to the data.
Substituting the regression coefficients in figure 16 and figure 17 with their corresponding estimates shown in table 10, the prediction models for FI and PDO crashes/mi/year are obtained as follows shown in figure 18 and figure 19*:
*Modified on November 16, 2014
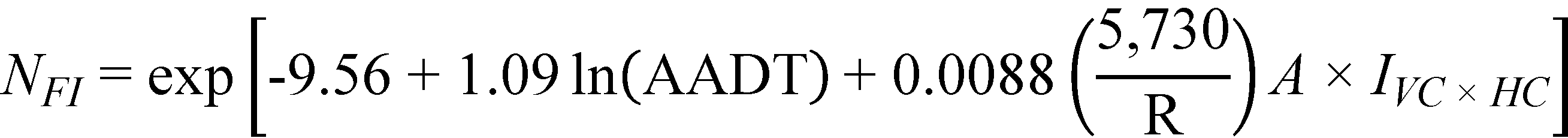
Figure 18. Equation. Predicted FI crashes on horizontal curves and tangents at type 1 crest vertical curves (explicit form).
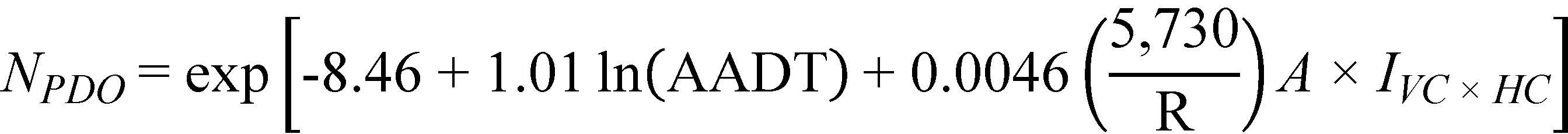
Figure 19. Equation. Predicted PDO crashes on horizontal curves and tangents at type 1 crest vertical curves (explicit form).
For horizontal curves and tangents at type 1 crest vertical curves, only the interaction term between curve radius (a characteristic of horizontal curves) and A, the algebraic difference in initial and final grades (a vertical curve characteristic), was found to be statistically significant. Crash frequency increased with the combination of decreasing curve radius and an increasing difference in grades.
Of interest is the fact that the marginal effect of the interaction, once the effect of AADT is accounted for, is very small as indicated by the extremely small chi-squared value in comparison to that for AADT (shown in table 10). After traffic volume was accounted for, there was little difference among the three roadway groups (i.e., level tangents, tangents on nonlevel grades, and horizontal curves at type 1 crest vertical curves). The argument can be made that the crash variability in all three groups was large (as seen in table 9). Additionally, the horizontal curves group consisted of only 87 mi of roadway as compared to the 833 mi of level tangents and 200 mi of tangents at type 1 crests.
In summary, the predictive model developed for type 1 crest vertical curves includes a term representing the interaction between the horizontal curve radius and the algebraic difference in grade for the crest vertical curve. The main effects of horizontal curve radius and algebraic difference in grade were not statistically significant. The interaction term indicates that the crash frequency increased as the horizontal curve radius decreased, the length of the vertical curve increased, and the sharpness of the vertical curve increased (i.e., as K decreases). This interaction term, while not nearly as strongly related to crash frequency as AADT, is potentially useful in the AASHTO HSM because it currently does not contain CMFs for crest vertical curves.(1)
A model with a main effect or interaction for K, representing the sharpness of the vertical curve, would potentially be more useful to designers than a model containing the algebraic difference in grade. However, neither the main effect of K nor any interactions involving K were statistically significant for type 1 crest vertical curves. The models in figure 18 and figure 19 can also be written with LVC/K substituted for A. The effect expressed in this form makes engineering sense as it indicates that crash frequency would increase as the length of the vertical curve increases and as the sharpness of the vertical curve increases (i.e., as K gets smaller). Therefore, it is suggested that figure 18 and figure 19 be recast as follows shown in figure 20 and figure 21*:
*Modified on November 16, 2014
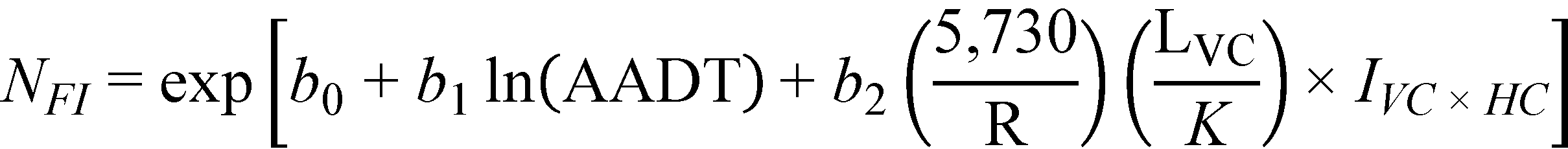
Figure 20. Equation. Predicted FI crashes on horizontal curves and tangents at type 1 crest vertical curves (alternate form).
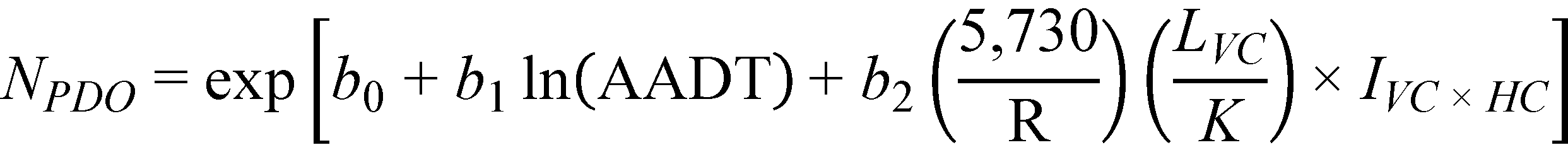
Figure 21. Equation. Predicted PDO crashes on horizontal curves and tangents at type 1 crest vertical curves (alternate form).
Horizontal Curves and Tangents at Type 1 Sag Vertical Curves
The following three alignment combinations shaded in figure 22 were included in the analysis:
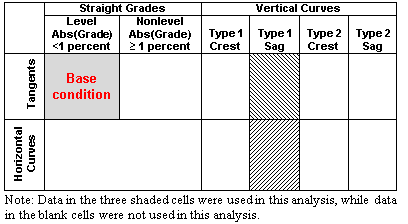
Figure 22. Illustration. Alignment combinations used in the analysis of horizontal curves and tangents at type 1 sag vertical curves.
Basic descriptive statistics such as sample size (i.e., number of roadway sections); total roadway length; and minimum, maximum, mean, and median values for specific parameters are shown in table 11 for each of the three alignment types included in the analysis.
Table 11. Descriptive statistics for horizontal curves and tangents at type 1 sag vertical curves.
Parameter |
Minimum |
Maximum |
Mean |
Median |
|
Horizontal Curves at Type 1 Sag Vertical Curves |
|||||
AADT (vehicles/day) |
169 |
19,373 |
3,074 |
1,821 |
|
Section length (mi) |
0.01 |
0.31 |
0.06 |
0.05 |
|
Horizontal curve length (mi) |
0.01 |
1.00 |
0.15 |
0.12 |
|
Curve radius (ft) |
100 |
11,459 |
2,085 |
1,433 |
|
Vertical curve length (ft) |
92 |
2,200 |
545 |
500 |
|
A |
1.0 |
13.0 |
4.4 |
3.8 |
|
K |
10.4 |
966.2 |
153.2 |
116.4 |
|
FI crashes per MVMT |
0 |
36.61 |
0.71 |
0 |
|
PDO crashes per MVMT |
0 |
21.35 |
0.81 |
0 |
|
Total crashes per MVMT |
0 |
52.06 |
1.53 |
0 |
|
Tangents at Type 1 Sag Vertical Curves |
|||||
AADT (vehicles/day) |
175 |
26,088 |
3,098 |
1,828 |
|
Section length (mi) |
0.01 |
0.51 |
0.07 |
0.06 |
|
Horizontal curve length (mi) |
|
|
|
|
|
Curve radius (ft) |
|
|
|
|
|
Vertical curve length (ft) |
60 |
2,800 |
523 |
400 |
|
A |
1.0 |
15.1 |
4.2 |
3.6 |
|
K |
6.8 |
969.7 |
153.0 |
120.2 |
|
FI crashes per MVMT |
0 |
46.26 |
0.48 |
0 |
|
PDO crashes per MVMT |
0 |
40.11 |
0.65 |
0 |
|
Total crashes per MVMT |
0 |
70.19 |
1.12 |
0 |
|
Level Tangents—Base Condition |
|||||
AADT (vehicles/day) |
169 |
26,088 |
3,287 |
2,160 |
|
Section length (mi) |
0.01 |
2.10 |
0.15 |
0.09 |
|
Horizontal curve length (mi) |
|
|
|
|
|
Curve radius (ft) |
|
|
|
|
|
Vertical curve length (ft) |
|
|
|
|
|
A |
|
|
|
|
|
K |
|
|
|
|
|
FI crashes per MVMT |
0 |
34.21 |
0.46 |
0 |
|
PDO crashes per MVMT |
0 |
39.50 |
0.67 |
0 |
|
Total crashes per MVMT |
0 |
55.38 |
1.14 |
0 |
|
The final crash prediction models for FI and PDO crashes are as follows shown in figure 23 and figure 24*:
*Modified on November 16, 2014
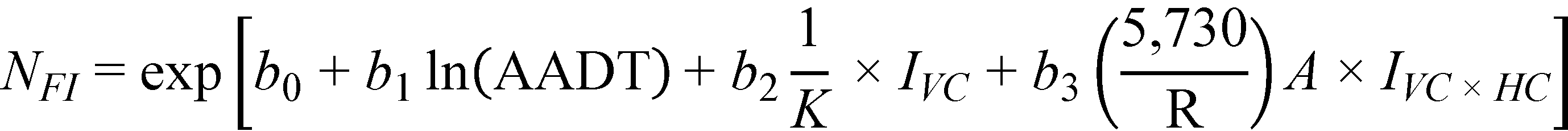
Figure 23. Equation. Predicted FI crashes on horizontal curves and tangents at type 1 sag vertical curves (general form).
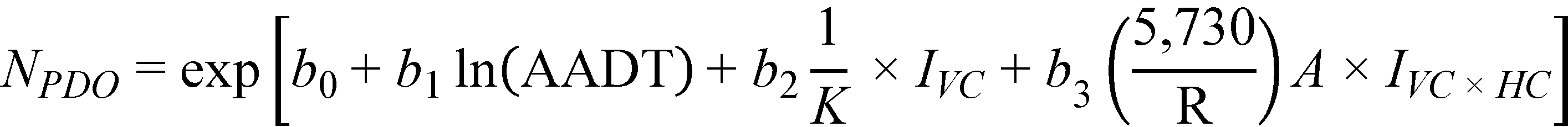
Figure 24. Equation. Predicted PDO crashes on horizontal curves and tangents at type 1 sag vertical curves (general form).
Where:
K = LVC/A; not applicable for level tangents.
LVC = Vertical curve length (ft).
IVC = Vertical curve indicator (1 for vertical curves; 0 otherwise).
The regression results, including all statistically significant parameters and interaction, are shown in table 12.
Table 12. FI and PDO crash modeling results for horizontal curves and tangents at type 1 sag vertical curves.
Parameter |
Regression |
Coefficient |
Standard |
Lower |
Upper |
Chi- |
Significance |
FI Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-9.55 |
0.24 |
-10.02 |
-9.08 |
N/A |
N/A |
ln(AADT) |
b1 |
1.10 |
0.03 |
1.04 |
1.15 |
1,516.6 |
< 0.0001 |
1/K |
b2 |
10.51 |
5.18 |
0.36 |
20.66 |
3.9 |
0.048 |
1/R × A interactiona |
b3 |
0.011 |
0.003 |
0.005 |
0.017 |
12.3 |
0.0005 |
Dispersion |
N/A |
0.86 |
0.06 |
0.75 |
0.99 |
N/A |
N/A |
PDO Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-8.63 |
0.20 |
-9.03 |
-8.24 |
||
ln(AADT) |
b1 |
1.03 |
0.03 |
0.98 |
1.08 |
1,776.9 |
< 0.0001 |
1/K |
b2 |
8.62 |
4.41 |
-0.02 |
17.26 |
3.7 |
0.055 |
1/R × A interactiona |
b3 |
0.010 |
0.002 |
0.005 |
0.014 |
16.7 |
< 0.0001 |
Dispersion |
N/A |
0.79 |
0.05 |
0.70 |
0.89 |
N/A |
N/A |
Using figure 8, the percentage of roadway segments with extremely high observed FI crash frequencies was 5.90 percent across all roadway segments, slightly above the expected 5 percent. The percentages of roadway segments with extremely high observed FI crash frequencies were 6.03 percent for level tangents, 5.23 percent for tangents at type 1 sags, and 6.51 percent for horizontal curves on type 1 sags, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
Similarly, the percentage of roadway segments with extremely high observed PDO crash frequencies was 6.60 percent across all roadway segments, slightly higher than that for FI crashes. The percentages were 6.79 percent for level tangents, 6.39 percent for tangents at type 1 sags, and 5.90 percent for horizontal curves on type 1 sags, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
The average probability of predicting a more extreme than observed FI crash frequency was calculated using figure 7. Across all roadway segments, the average probability was 0.13. The probability was 0.14 for level tangents, 0.11 for tangents at type 1 sags, and 0.12 for horizontal curves on type 1 sags, which were all considerably lower than the theoretically expected value of 0.25.
Similarly, the average probability of predicting a more extreme than observed PDO crash frequency was 0.15 across all roadway segments. The probability was 0.16 for level tangents, 0.14 for tangents on type 1 sags, and 0.14 for horizontal curves on type 1 sags, which were all considerably lower than the theoretically expected value of 0.25. For both FI and PDO crashes, these low probabilities indicate that the model might not provide an adequate fit to the data.
Substituting the regression coefficients in figure 23 and figure 24 with their corresponding estimates in table 12, the prediction models for FI and PDO crashes/mi/year are as follows shown in figure 25 and figure 26*:
*Modified on November 16, 2014
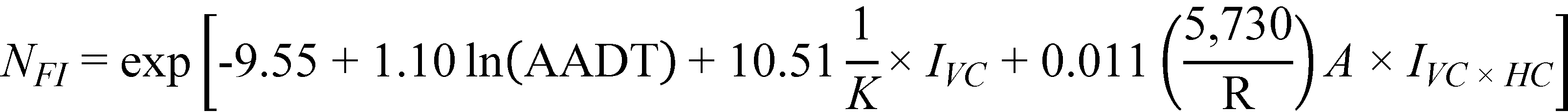
Figure 25. Equation. Predicted FI crashes on horizontal curves and tangents at type 1 sag vertical curves (explicit form).
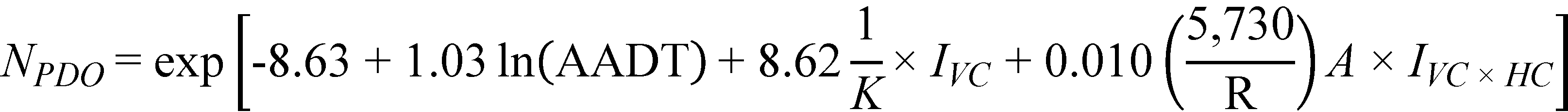
Figure 26. Equation. Predicted PDO crashes on horizontal curves and tangents at type 1 sag vertical curves (explicit form).
For horizontal curves and tangents at type 1 sag vertical curves, the inverse of K, a measure of vertical curvature, and the interaction term between curve radius (a characteristic of horizontal curves) and A (a vertical curve characteristic) were found to be statistically significant in both models. These models show that crash frequency increases with decreasing K (i.e., with sharper sags). The interaction term between R and A shows that crash frequency increases with the decreasing curve radius and increasing difference in grades. In both models, the effect of the interaction is greater than that of K as reflected in the comparison of their chi-squared values in table 12.
As noted earlier for the crash model at type 1 crest vertical curves shown in figure 18, figure 19, and table 10, the marginal effect of the parameters in each model after the effect of AADT is accounted for is small, as indicated by the small chi-squared values in comparison to that for AADT (see table 12). This is an indication that after traffic volume is accounted for, there is little difference among the three groups of roadway (i.e., level tangents, tangents on nonlevel grades, and horizontal curves at type 1 sag vertical curves). The argument can be made that the crash variability in all three groups is large (see in table 11). Additionally, the horizontal curves group consists of only 57 mi of roadway as compared to the 833 mi of level tangents and 145 mi of tangents at type 1 sags.
As in the case for type 1 crest vertical curves, it makes engineering sense to replace A with LVC/K in figure 25 and figure 26. In this form, both the main effect and the interaction term include K
in the denominator rather than having an inconsistency with the main effect including K and
the interaction including A. Thus, it is recommended that figure 25 and figure 26 be recast
as follows shown in figure 27 and figure 28*:
*Modified on November 16, 2014
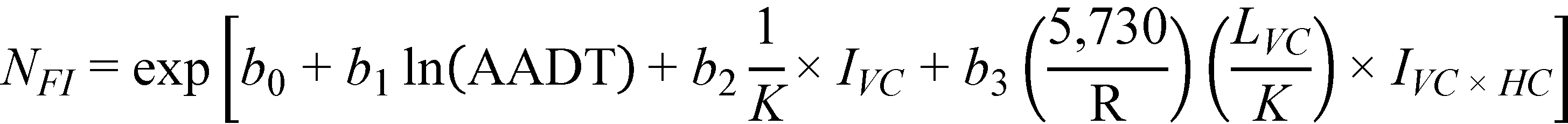
Figure 27. Equation. Predicted FI crashes on horizontal curves and tangents at type 1 sag vertical curves (alternate form).
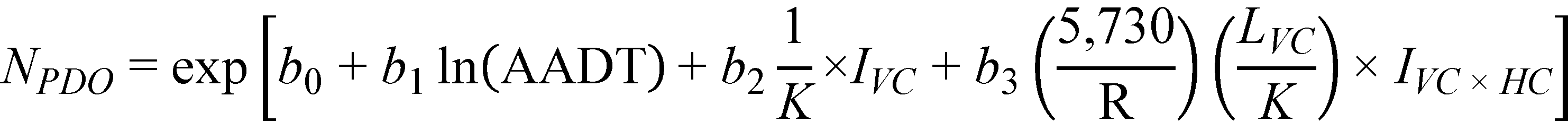
Figure 28. Equation. Predicted PDO crashes on horizontal curves and tangents at type 1 sag vertical curves (alternate form).
In summary, the predictive model developed for type 1 sag vertical curves includes a term representing the sharpness of the vertical curve as a main effect and an interaction between the horizontal curve radius, the vertical curve length, and the sharpness of the vertical curve. The model indicates that crash frequency increases as the horizontal curve radius decreases, the length of the vertical curve increases, and the sharpness of the vertical curve increases (i.e., as K decreases). The main effect and the interaction, while not as strongly related to crash frequency as AADT, are potentially useful in the AASHTO HSM because it does not currently contain CMFs for sag vertical curves.(1)
Horizontal Curves and Tangents at Type 2 Crest Vertical Curves
The following three alignment combinations shaded in figure 29 were included in the analysis:
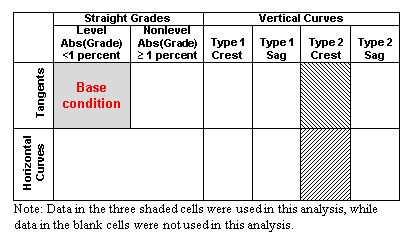
Figure 29. Illustration. Alignment combinations used in the analysis of horizontal curves and tangents at type 2 crest vertical curves.
Basic descriptive statistics such as sample size (i.e., number of roadway sections); total roadway length; and minimum, maximum, mean, and median values for specific parameters are shown in table 13 for each of the three alignment types included in the analysis.
Table 13. Descriptive statistics for horizontal curves and tangents at type 2 crest vertical curves.
Parameter |
Minimum |
Maximum |
Mean |
Median |
||
Horizontal Curves at Type 2 Crest Vertical Curves |
||||||
AADT (vehicles/day) |
202 |
20,931 |
2,603 |
1,607 |
||
Section length (mi) |
0.01 |
0.34 |
0.06 |
0.05 |
||
Horizontal curve length (mi) |
0.01 |
1.09 |
0.16 |
0.12 |
||
Curve radius (ft) |
100 |
11,459 |
1,960 |
1,433 |
||
Vertical curve length (ft) |
75 |
2,400 |
543 |
400 |
||
A |
1.0 |
8.3 |
2.8 |
2.4 |
||
K |
15.9 |
952.4 |
227.0 |
178.8 |
||
FI crashes per MVMT |
0 |
28.16 |
0.63 |
0 |
||
PDO crashes per MVMT |
0 |
30.02 |
0.87 |
0 |
||
Total crashes per MVMT |
0 |
30.02 |
1.50 |
0 |
||
Tangents at Type 2 Crest Vertical Curves |
||||||
AADT (vehicles/day) |
175 |
21,825 |
2,741 |
1,652 |
||
Section length (mi) |
0.01 |
0.38 |
0.07 |
0.06 |
||
Horizontal curve length (mi) |
|
|
|
|
||
Curve radius (ft) |
|
|
|
|
||
Vertical curve length (ft) |
60 |
2,400 |
498 |
400 |
||
A |
1.0 |
8.0 |
2.6 |
2.2 |
||
K |
16.2 |
985.9 |
222.4 |
176.3 |
||
FI crashes per MVMT |
0 |
36.12 |
0.42 |
0 |
||
PDO crashes per MVMT |
0 |
27.05 |
0.61 |
0 |
||
Total crashes per MVMT |
0 |
36.12 |
1.03 |
0 |
||
Level Tangents—Base Condition |
||||||
AADT (vehicles/day) |
169 |
26,088 |
3,287 |
2,160 |
||
Section length (mi) |
0.01 |
2.10 |
0.15 |
0.09 |
||
Horizontal curve length (mi) |
|
|
|
|
||
Curve radius (ft) |
|
|
|
|
||
Vertical curve length (ft) |
|
|
|
|
||
A |
|
|
|
|
||
K |
|
|
|
|
||
FI crashes per MVMT |
0 |
34.21 |
0.46 |
0 |
||
PDO crashes per MVMT |
0 |
31.60 |
0.66 |
0 |
||
Total crashes per MVMT |
0 |
36.34 |
1.12 |
0 |
||
Note: No roadway segments exist in the shaded cells.
The final crash prediction models for FI and PDO crashes are as follows shown in figure 30 and figure 31*:
*Modified on November 16, 2014
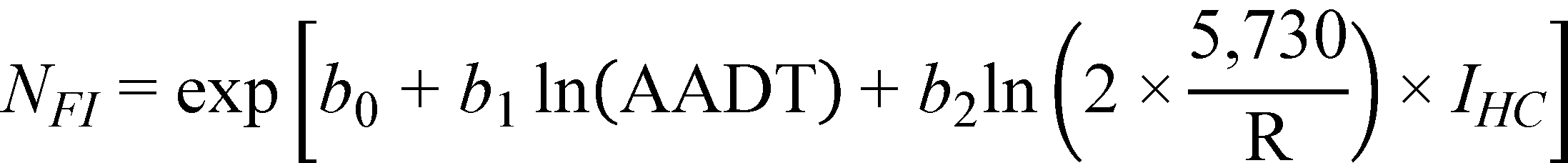
Figure 30. Equation. Predicted FI crashes on horizontal curves and tangents at type 2 crest vertical curves (general form).
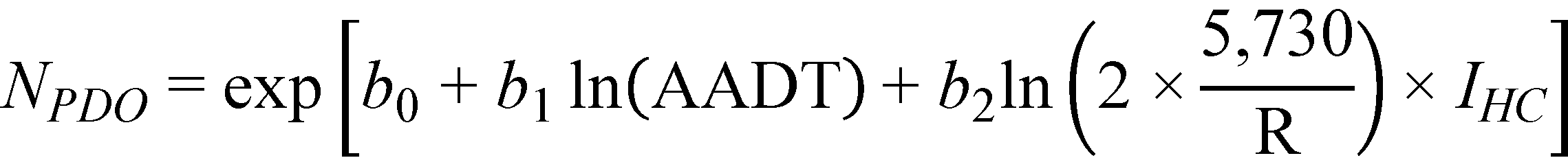
Figure 31. Equation. Predicted PDO crashes on horizontal curves and tangents at type 2 crest vertical curves (general form).
The regression results, including all statistically significant parameters, are shown in table 14. There were no statistically significant interactions for type 2 crest vertical curves.
Using figure 8, the percentage of roadway segments with extremely high observed FI crash frequencies was 6.46 percent across all roadway segments, slightly above the expected percentage, which was 5 percent. The percentages of roadway segments with extremely high observed FI crash frequencies were 6.46 percent for level tangents, 5.84 percent for tangents at type 2 crests, and 7.55 percent for horizontal curves on type 2 crests, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
Table 14. FI and PDO crash modeling results for horizontal curves and tangents at type 2 crest vertical curves.
Parameter |
Regression |
Coefficient |
Standard |
Lower |
Upper |
Chi- |
Significance |
FI Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-9.52 |
0.24 |
-9.99 |
-9.05 |
N/A |
N/A |
ln(AADT) |
b1 |
1.09 |
0.03 |
1.03 |
1.14 |
1,470.5 |
< 0.0001 |
1/R terma |
b2 |
0.20 |
0.04 |
0.12 |
0.28 |
20.4 |
< 0.0001 |
Dispersion |
N/A |
0.67 |
0.06 |
0.57 |
0.79 |
N/A |
N/A |
PDO Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-8.38 |
0.20 |
-8.78 |
-7.99 |
N/A |
N/A |
ln(AADT) |
b1 |
1.00 |
0.02 |
0.95 |
1.05 |
1,699.0 |
< 0.0001 |
1/R terma |
b2 |
0.10 |
0.04 |
0.03 |
0.18 |
6.6 |
0.010 |
Dispersion |
N/A |
0.65 |
0.05 |
0.57 |
0.74 |
N/A |
N/A |
The percentage of roadway segments with extremely high observed PDO crash frequencies was 6.93 percent across all roadway segments, slightly higher than that for FI crashes. The percentages were 6.99 percent for level tangents, 6.61 percent for tangents at type 2 crests, and 7.16 percent for horizontal curves on type 2 crests, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
The average probability of predicting a more extreme than observed FI crash frequency was calculated using figure 7. Across all roadway segments, the average probability was 0.12. The probability was 0.13 for level tangents, 0.09 for tangents at type 2 crests, and 0.11 for horizontal curves on type 2 crests, which were all considerably lower than the theoretically expected value of 0.25.
Similarly, the average probability of predicting a more extreme than observed PDO crash frequency was 0.14 across all roadway segments. The probability was 0.16 for level tangents, 0.12 for tangents on type 2 crests, and 0.12 for horizontal curves on type 2 crests, which were all considerably lower than the theoretically expected value of 0.25. For both FI and PDO crashes, these low probabilities indicate that the model might not provide an adequate fit to the data.
Substituting the regression coefficients in figure 30 and figure 31 with their corresponding estimates in table 14, the prediction models for FI and PDO crashes/mi/year are as follows shown in figure 32 and figure 33*:
*Modified on November 16, 2014
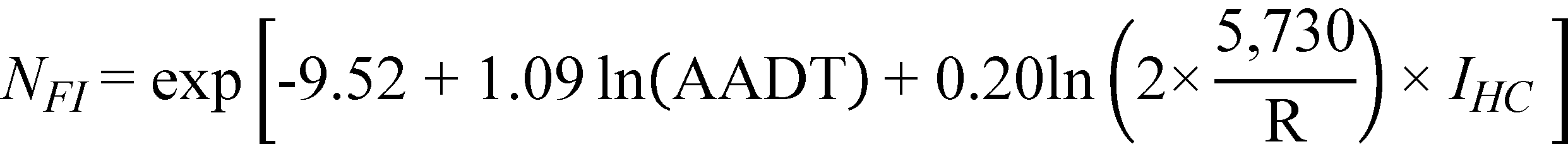
Figure 32. Equation. Predicted FI crashes on horizontal curves and tangents at type 2 crest vertical curves (explicit form).
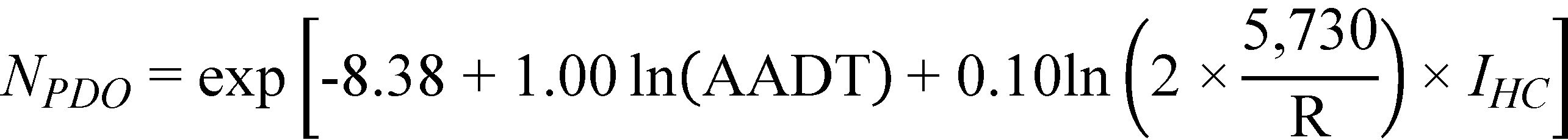
Figure 33. Equation. Predicted PDO crashes on horizontal curves and tangents at type 2 crest vertical curves (explicit form).
The horizontal curves group consists of only 62 mi of roadway as compared to the 833 mi of level tangents and 132 mi of tangents at type 2 crests. For horizontal curves and tangents at type 2 crest vertical curves, curve radius (a characteristic of horizontal curves) was the only parameter found to be statistically significant in both models. Although its effect is more pronounced for FI than for PDO crashes, it is small compared to that of AADT. It is interesting to note that the effect of curve radius for horizontal curves and tangents at type 2 crest vertical curves is comparable to the effect of curve radius for horizontal curves on straight grades (compare coefficient estimates in table 14 to those in table 8).
The models developed for type 2 crest vertical curves include a main effect for horizontal curve radius but no effect for any vertical curve elements. This makes the models for type 2 crest vertical curves less useful than the models for type 1 crest vertical curves. Sensitivity analyses are needed to establish whether the straight grade models in figure 10 and figure 11 might be applied to type 2 crest vertical curves, with G set equal to the average of G1 and G2 instead of figure 32 and figure 33.
Horizontal Curves and Tangents at Type 2 Sag Vertical Curves
The following three alignment combinations shaded in figure 34 were included in the analysis:

Figure 34. Illustration. Alignment combinations used in the analysis of horizontal curves and tangents at type 2 sag vertical curves.
Basic descriptive statistics such as sample size (i.e., number of roadway sections); total roadway length; and minimum, maximum, mean, and median values for specific parameters are shown in table 15 for each of the three alignment types included in the analysis.
Table 15. Descriptive statistics for horizontal curves and tangents at type 2 sag vertical curves.
Parameter |
Minimum |
Maximum |
Mean |
Median |
Horizontal Curves at Type 2 Sag Vertical Curves |
||||
AADT (vehicles/day) |
175 |
21,825 |
2,691 |
1,742 |
Section length (mi) |
0.01 |
0.30 |
0.05 |
0.04 |
Horizontal curve length (mi) |
0.01 |
1.09 |
0.17 |
0.13 |
Curve radius (ft) |
100 |
11,459 |
1,964 |
1,433 |
Vertical curve length (ft) |
60 |
1,600 |
424 |
400 |
A |
1.0 |
7.7 |
2.7 |
2.5 |
K |
9.7 |
917.4 |
185.6 |
149.3 |
FI crashes per MVMT |
0 |
26.06 |
0.60 |
0 |
PDO crashes per MVMT |
0 |
27.82 |
0.95 |
0 |
Total crashes per MVMT |
0 |
27.82 |
1.54 |
0 |
Tangents at Type 2 Sag Vertical Curves |
||||
AADT (vehicles/day) |
169 |
23,334 |
2,909 |
1,776 |
Section length (mi) |
0.01 |
0.38 |
0.06 |
0.05 |
Horizontal curve length (mi) |
|
|
|
|
Curve radius (ft) |
|
|
|
|
Vertical curve length (ft) |
60 |
2,000 |
400 |
400 |
A |
1.0 |
7.6 |
2.6 |
2.2 |
K |
16.2 |
970.9 |
184.3 |
148.1 |
FI crashes per MVMT |
0 |
27.82 |
0.44 |
0 |
PDO crashes per MVMT |
0 |
28.27 |
0.61 |
0 |
Total crashes per MVMT |
0 |
38.20 |
1.05 |
0 |
Level Tangents—Base Condition |
||||
AADT (vehicles/day) |
169 |
26,088 |
3,288 |
2,160 |
Section length (mi) |
0.01 |
2.10 |
0.15 |
0.09 |
Horizontal curve length (mi) |
|
|
|
|
Curve radius (ft) |
|
|
|
|
Vertical curve length (ft) |
|
|
|
|
A |
|
|
|
|
K |
|
|
|
|
FI crashes per MVMT |
0 |
34.21 |
0.46 |
0 |
PDO crashes per MVMT |
0 |
25.79 |
0.66 |
0 |
Total crashes per MVMT |
0 |
36.34 |
1.12 |
0 |
Note: No roadway segments exist in the shaded cells.
The final crash prediction models for FI and PDO crashes are shown in figure 35 and figure 36*:
*Modified on November 16, 2014
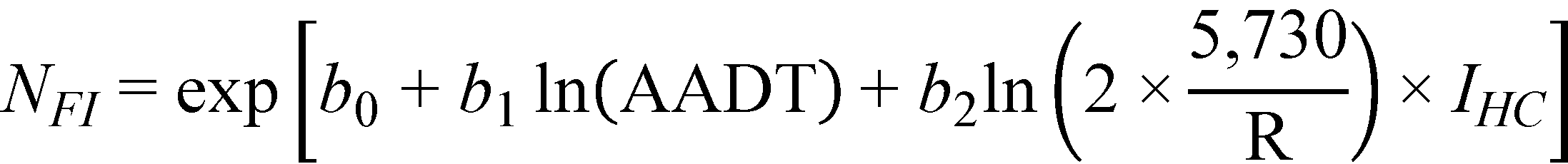
Figure 35. Equation. Predicted FI crashes on horizontal curves and tangents at type 2 sag vertical curves (general form).
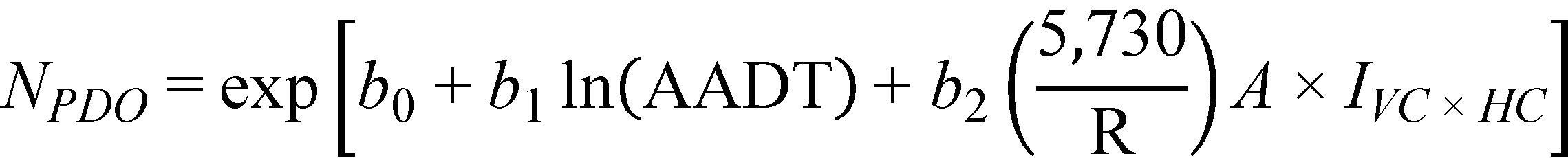
Figure 36. Equation. Predicted PDO crashes on horizontal curves and tangents at type 2 sag vertical curves (general form).
The regression results, including all statistically significant parameters and interaction, are shown in table 16.
Table 16. FI and PDO crash modeling results for horizontal curves and tangents at type 2 sag vertical curves.
Parameter |
Regression |
Coefficient |
Standard |
Lower |
Upper |
Chi- |
Significance |
FI Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-9.42 |
0.24 |
-9.90 |
-8.95 |
N/A |
N/A |
ln(AADT) |
b1 |
1.08 |
0.03 |
1.02 |
1.13 |
1,427.2 |
< 0.0001 |
1/R terma |
b2 |
0.188 |
0.04 |
0.11 |
0.27 |
18.2 |
< 0.0001 |
Dispersion |
N/A |
0.76 |
0.06 |
0.65 |
0.88 |
NA |
NA |
PDO Crashes/Mi/Year |
|||||||
Intercept |
b0 |
-8.30 |
0.20 |
-8.69 |
-7.90 |
N/A |
N/A |
ln(AADT) |
b1 |
0.99 |
0.02 |
0.94 |
1.03 |
1,648.2 |
< 0.0001 |
1/R × A interactionb |
b2 |
0.022 |
0.005 |
0.013 |
0.031 |
20.8 |
< 0.0001 |
Dispersion |
N/A |
0.64 |
0.05 |
0.56 |
0.73 |
N/A |
N/A |
Using figure 8, the percentage of roadway segments with extremely high observed FI crash frequencies was 6.08 percent across all roadway segments, which was slightly above the expected percentage of 5 percent. The percentage of roadway segments with extremely high observed FI crash frequencies was 6.24 percent for level tangents, 5.53 percent for tangents at type 2 sags, and 6.32 percent for horizontal curves on type 2 sags, indicating that a few roadway segments in these categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
Similarly, the percentage of roadway segments with extremely high observed PDO crash frequencies was 6.99 percent across all roadway segments, which was slightly higher than that for FI crashes. The percentages were 7.10 percent for level tangents, 6.46 percent for tangents at type 2 sags, and 7.42 percent for horizontal curves on type 2 sags, indicating that a few roadway segments in these roadway categories experienced unusually high FI crash frequencies given the prediction model used. None of the segments experienced extremely low FI crash frequencies under the assumed model at the 5 percent significance level.
The average probability of predicting a more extreme than observed FI crash frequency was calculated using figure 7. Across all roadway segments, the average probability was 0.12. The probability was 0.13 for level tangents, 0.09 for tangents at type 2 sags, and 0.10 for horizontal curves on type 2 sags, which were all considerably lower than the theoretically expected value of 0.25.
Similarly, the average probability of predicting a more extreme than observed PDO crash frequency was 0.14 across all roadway segments. The probability was 0.16 for level tangents, 0.12 for tangents on type 2 sags, and 0.12 for horizontal curves on type 2 sags, which were all considerably lower than the theoretically expected value of 0.25. For both FI and PDO crashes, these low probabilities indicate that the model might not provide an adequate fit to the data.
Substituting the regression coefficients in figure 35 and figure 36 with their corresponding estimates in table 16, the prediction models for FI and PDO crashes/mi/year are as follows shown in figure 37 and figure 38*:
*Modified on November 16, 2014
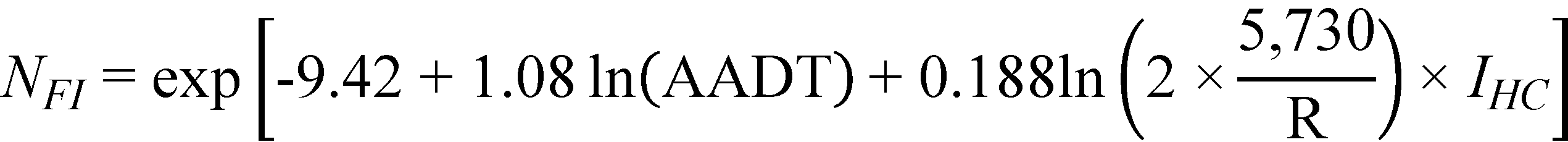
Figure 37. Equation. Predicted FI crashes on horizontal curves and tangents at type 2 sag vertical curves (explicit form).
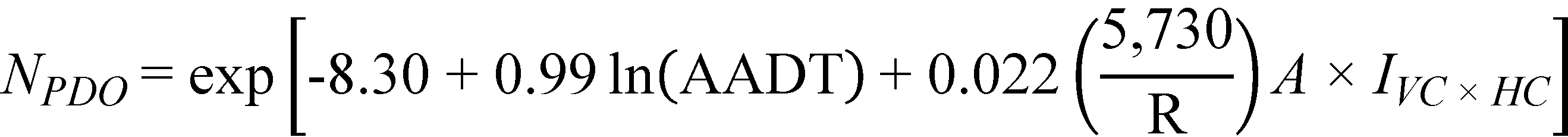
Figure 38. Equation. Predicted PDO crashes on horizontal curves and tangents at type 2 sag vertical curves (explicit form).
The horizontal curves group consists of only 63 mi of roadway as compared to 833 mi of level tangents and 129 mi of tangents at type 2 sags. For horizontal curves and tangents at type 2 sag vertical curves, curve radius (a characteristic of horizontal curves) was the only parameter found to be statistically significant in the FI crash prediction model. The model in figure 37 shows that FI crash frequency increases with decreasing curve radius, as expected. For the PDO crash prediction model, only the interaction term between curve radius (a characteristic of horizontal curves) and A (a vertical curve characteristic), was found to be statistically significant. The model in figure 38 shows that crash frequency increases with the combination of decreasing curve radius and increasing difference in grades.
In either model, the effect of the significant parameter or interaction of parameters is more pronounced than in previous models as reflected in the slightly higher chi-squared values. The magnitude of the coefficients is consistent between this set of models and previous models. There is a substantial inconsistency between the FI and PDO crash models for type 2 sag vertical curves in that the PDO crash model includes a statistically significant interaction between horizontal curve radius and algebraic difference in grade, but the FI crash model does not. This is the only situation in the study where different parameters or functional forms had to be used for the corresponding FI and PDO crash models. This inconsistency makes the models for type 2 sag vertical curves less useful than the models for type 1 sag vertical curves. LVC/K could be substituted for A in figure 38, as was done for type 1 crest vertical curves and type 1 sag vertical curves, but it seems pointless to do this in the PDO crash model when the more important FI crash model does not include a similar interaction term. Sensitivity analyses might establish whether, as an alternative to the inconsistent models in figure 37 and figure 38, the straight grade models in figure 10 and figure 11 might be applied to type 2 sag vertical curves with the value of G set equal to the average of G1 and G2.
STUDY LIMITATIONS
The major limitation of the study results is that data from only one State were used in the analysis. It would have been desirable to use data from additional States, but Washington is the only known State for which curve and grade data are available for the entire State highway system in a form that can be linked to crash data.
The study divided the roadway into segments for analysis. A new segment started at each point where a horizontal curve or vertical alignment feature (straight grade or vertical curve) began or ended. Segmenting the roadway in this way resulted in a number of very short segments. The shortest of these segments were dropped from the analysis, but some of the segments that were analyzed may be shorter than the expected accuracy of reported crash locations. Nevertheless, this approach to segmenting roadways appears to be the best method to the authors of this report for analyzing these data because the geometrics of each analysis section are known to be homogeneous with respect to horizontal and vertical alignment features. Alternative analysis approaches that use fixed-length study sections (typically 0.5 or 1.0 mi long) and model the percentage of section length over which particular geometric features (or combinations of features) are present do not appear likely to provide satisfactory results for this application.
As noted earlier, the analysis considered the effects of horizontal and vertical geometrics on crashes but did not consider other features known to affect crashes such as lane and shoulder widths. In fact, the AASHTO HSM includes 12 factors that are known to affect safety on rural two lane highways.(1) Consideration of all these factors was not beyond the scope of this current study. A future study is necessary to develop safety prediction models for rural two-lane highways considering all 12 factors and their interactions.