U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-15-047 Date: August 2015 |
Publication Number: FHWA-HRT-15-047 Date: August 2015 |
This literature review considers all aspects of the project that were investigated. The first aspect is roadway lighting and the overall impact of spectrum on human vision. The second component covers the mechanisms for describing visual performance and calculating the impact of lighting conditions on the detection of objects in the roadway. The third component considers mesopic models. Finally, the fourth component describes the MPI system.
Although 25-percent less travel occurs at night compared with daytime, more than 50 percent of all fatal crashes occur at night. The fatality rate (number of fatalities per 100 million vehicle-mi traveled) for drivers is three times higher at night compared with daylight conditions.(7–9)
Roadway lighting has long been used as a crash countermeasure, and the link between crash safety and lighting level has been established through several investigations. (See references 10–15). In the most recent study, Gibbons et al. show that there is a significant link between lighting level and crash safety based on roadway type.(16,17) These investigations consider roadway lighting design criteria such as luminance (how much light is reflected from the roadway toward the eye of the observer) and uniformity (how evenly the light is distributed on the roadway), but none of these investigations have used the color of the light source as a design criterion.
The color of the lighting for the roadway light source has recently become a more critical issue in roadway lighting design, but as yet, it is not accounted for in lighting design criteria.(5) The human eye responds to electromagnetic waves in the range of about 360 to 800 nm. This is known as the visible light spectrum. The light emitted from a light source on a wavelength-by-wavelength basis is called spectral power distribution (SPD). The SPD is a result of the physics of how the light is produced (i.e., arc tube, emission, phosphor transition, LED, etc.) and can be broadband, with emissions across all of the visible light spectrum, or narrowband, with emissions in only a small portion of the spectrum. As an example, the SPD of an HPS lamp and three types of LED sources are shown in figure 1 and figure 2. Here the HPS lamp would be classified as narrowband because it does not have significant output below 500 nm (blue), whereas the LED sources would be considered broad spectrum because they have output across the entire spectrum. The other curves in the figure, V(λ) and V'( λ) represent human visual response at high (daytime) illuminance levels and low (nighttime) illuminance levels, respectively.
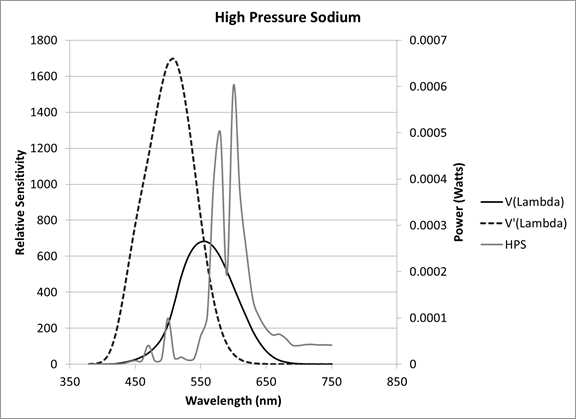
Figure 1. Graph. Spectral power distribution of HPS light sources.(18)
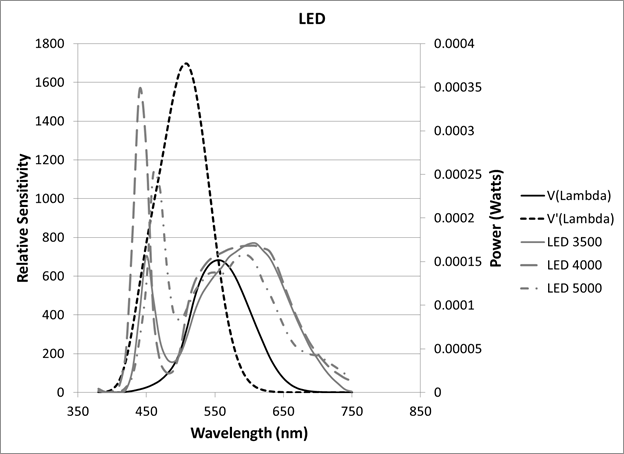
Figure 2. Graph. Spectrum power distribution of three LED light sources.(18)
Light sources have a color component typically measured in correlated color temperature (CCT) measured in Kelvin (K). The CCT is a measure of how the appearance of a light source relates to the temperature of a black body radiator. As the radiator is heated, it typically changes from appearing as yellow toward blue as the temperature rises. This color shift is shown in figure 3. Typically, light sources that are 3,000 K and higher are categorized as white sources because their output is broad spectrum, and they do not have gaps in their color output.
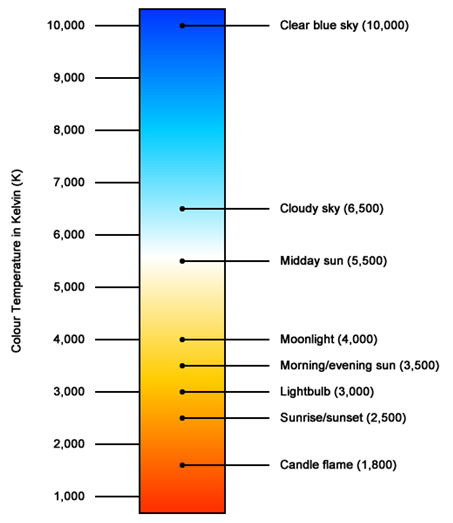
Figure 3. Diagram. Change in light source appearance with CCT.(18)
Recent research has shown a benefit of broad-spectrum light in the detection of objects along the side of a roadway when compared with traditional narrow-spectrum light sources. (See references 19–23.) The potential of this benefit is that a lower light level provides the same visual performance under broad spectrum sources as a higher light level under a narrowband source. This benefit may be a result of the responsiveness of the human eye to lower levels of light (mesopic vision issues), or it may be a result of color information provided by the light source in the visual application. The potential for having similar visual performance with reduced lighting levels translates directly to reduced energy costs while maintaining driver safety. The magnitude of this benefit in an actual driving environment, as well as its relationship to the spectral character of the light source, is unknown.
Shaflik detailed differing light types, their colors, and the issues with these light types.(24) Table 1 is derived from this information. Shaflik notes that blue and white light sources are more preferred by the general public, but town planners and astronomers resist them because of light trespass and light pollution issues. From Shaflik’s review, most blue and white light sources tend to be more energy-inefficient than HPS light sources, which lack color-rendering capabilities and are less preferred by motorists. It should be noted that Shaflik’s review was in 1997, before the advent of high-power LED sources, and he does not consider them in his review.
Table 1. Light type, color, and problems (from Shaflik, 1997).(24)
Light Type |
Color |
Problem |
| Mercury vapor | Blue-white | Energy inefficient |
| Metal halide | White | Lower efficiency, upward sky glow |
| High-pressure sodium | Amber-pink | Poor color rendition |
| Low pressure sodium | Amber-orange | Very poor color rendition |
Terry and Gibbons compared two LED luminaires of 3,500- and 6,000-K correlated color temperature to a 4,200-K fluorescent luminaire for the detection and color recognition of small targets and pedestrians.(25) Pedestrians were clad in two different colors, and the small targets were painted four different colors. Their results were mixed. The 3,500- and 6,000-K sources were nearly equal in terms of target color recognition distance; however, the 6,000-K luminaires outperformed the 3,500-K luminaires in pedestrian clothing color recognition distance by nearly 30 percent. The 4,200-K fluorescent light outperformed both LEDs for small target color recognition, but for pedestrian clothing color recognition, the 4,200-K fluorescent light was found to be equal to the 3,500-K LED. When considering both detection distance and color recognition distance, the authors suggested that the 6,000-K LED might be the superior light type for rendering color. The differences in color recognition between small targets and pedestrians were likely a result of the chosen colors for each: pedestrians wore black or denim scrubs, while targets were red, blue, gray, or green.
The nature of the lighting conditions for a nighttime driver can define how the spectral output from a light source affects the driver’s vision. Eye performance changes based on the ambient light level surrounding the driver. This process is typically called dark adaptation and represents both changes in overall sensitivity as well as the spectral response of the eye. The dark adaptation process represents the transition between the two types of photoreceptors in the retina: the rod and cone systems.
At high light levels, where visual field luminances are in excess of approximately 3.4 cd/m2 (.99fL) (about early twilight level) conditions are considered to be photopic, and human eye response follows a curve known as V(λ). When the light level is very low (well below moonlight levels, less than 0.001 cd/m2 (0.0003 fL)), the conditions are described as scotopic. Conditions between these two levels are referred to as mesopic, which is typically where roadway lighting levels fall. In the mesopic range, both rods and cones are active, and visual sensitivity is a combination of the two sensitivity functions. 1 cd/m2 = 0.3 fL
Figure 4 illustrates these ranges.(26) This figure also illustrates typical recommended street and roadway lighting levels, in terms of averages and minima, for Illuminating Engineering Society of North America and Commission Internationale d’Eclairage (CIE) practice.(1,26) Lighting levels for security are generally in the same range or lower and are usually specified in terms of illuminance.
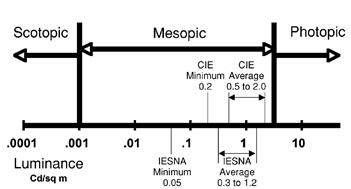
Source: IES
1 cd/m2 = 0.3 fL
Figure 4. Diagram. Ranges of visual sensitivity.(18)
The spectral response of the eye is also a result of the cone/rod transition. The spectral response of the cone system, active at high lighting levels, corresponds to the photopic V(λ) sensitivity curve, which peaks at 507nm. Thus, at the transition between photopic and scotopic lighting levels during dark adaptation, the eye’s maximum sensitivity changes from green in photopic conditions to blue-green in scotopic conditions. This effect—the well-known Purkinje shift, where the eye’s sensitivity shifts from longer to shorter wavelengths—has been known for more than a century.
One of the difficulties with this spectral change is that it unevenly affects the retina. It is based on the relative densities of the rods and cones and receptor areas across the retina. In the retinal periphery, the rod-dominated receptive fields outweigh the cone-dominated fields, which creates a stronger mesopic effect in that portion of the visual field. In the fovea centralis, the central portion of the retina that provides maximum visual resolution, and at adaptation levels sufficient to stimulate the small cone-dominated receptive fields, there is no rod contribution, which means there is no mesopic impact in this region. Therefore, because the mesopic effect varies across the retina, care must be taken in the design and application of an experiment to provide visual tasks that are both fovea based and periphery based.
One of the important aspects of this effect of dark adaptation is that the specifications for light outputs of light sources are determined using the photopic V(λ) curve. This means that all luminaires are characterized photopically, but their implementation in the roadway environment is mesopic, where the photopic curve does not accurately indicate their visual effect. However, the extent of any deviations between the photopic and mesopic conditions depends on the actual luminance levels and viewing conditions in the roadway.
To evaluate lighting systems in the mesopic adaptation range, a model of the sensitivity of the eye during the change from photopic into mesopic lighting conditions was established.
The luminous efficiency function, V(λ), is based on data collected in 1922-23 and was adopted in 1924 by the CIE for a central visual angle of 2 degrees.(27) It is the basis of most lighting measurements, as well as for manufacturer descriptions of a light source's output. Other luminous efficiency functions are V10(λ), the photopic luminous efficiency function for a visual angle of 10 degrees, and V′(λ), the scotopic luminous efficiency function, derived from data acquired at a visual angle of approximately 10 degrees.(27) The ratio of the lamp's scotopic output to its photopic output (S/P) is calculated using V(λ) and V′(λ), and describes the SPD of a light source in mesopic conditions. The models suggest that the higher a lamp's S/P ratio, the better its light is for peripheral detection in the mesopic region.(28,29)
For nighttime driving, in the mesopic vision region, V(λ)remains fairly accurate for foveal detection but does not describe the eye's behavior for the kind of off-axis vision commonly used in driving. A number of models using various combinations of the photopic and scotopic luminous efficiency functions have been developed in an effort to better describe mesopic vision. The models discussed here fall into two broad groups, based on how the data to create them were collected: brightness-matching models and performance-based models.
Any mesopic model that is to be implemented as a model of photometry must meet two basic requirements. First, the model should obey Abney’s Law of additivity, that the luminance of the light source is equal to the sum of its comprised wavelengths, which is a fundamental law of photometry. The second constraint is that the mesopic spectral sensitivity function should be the same as the photopic spectral sensitivity function, V(λ), at the upper end of the mesopic region, and also should be the same as the scotopic spectral sensitivity function, V′(λ), at the lower end of the mesopic region.
Brightness Matching
To develop a function for mesopic luminous efficiency, a number of researchers had participants view two adjacent semicircles of light and match them for brightness. The lower section was either white light or 570 nm, and the top section was light of varying wavelengths throughout the spectrum.(30–32) Observers identified the point when the two semicircles appeared equally bright; researchers then measured their comparative radiances to develop the luminous efficiency function. The resulting functions describe the mesopic luminosity of a light source as a linear relationship between the log of the mesopic luminous efficiency function and the sum of the photopic and scotopic luminous efficiency functions, each weighted by a factor that describes where in the mesopic region the test occurred. (See references 30, 32, 33, and 34.) Additional brightness-matching functions include contributions of the different types of cones.(35)
Brightness-matching functions accurately describe monochromatic light sources in the mesopic region. However, they are inaccurate when describing multichromatic sources such as roadway lighting. This is because humans perceive narrow-bandwidth saturated colors as brighter than other colors. Thus, two saturated colors together appear less bright than the sum of the constituent colors’ brightness, a phenomenon known as the Helmholtz-Kohlrauch effect.(35) Brightness matching is performed with narrow-bandwidth stimuli, so the resulting luminous efficiency function applies to those stimuli—but not multichromatic sources, which will appear dimmer than would be predicted by brightness-matching luminous efficiency functions.
The main problem with using brightness-matching models as a basis for photometry is that they tend to violate Abney’s law of additivity. This is because they account for interactions between chromatic and achromatic channels of the visual system, which are nonlinear in nature, thereby resulting in nonadditive models.
Performance-Based Models
X-Model:
In an effort to correct for problems with brightness-matching functions and to collect data on visual perception in a context more similar to driving, the X-model was developed using data collected with the binocular simultaneity method (BSM). The researchers’ goal was to create an easy-to-use model of mesopic vision, grounded in human vision, that does not suffer from additivity problems, using the familiar luminous efficiency functions V(λ) and V′(λ).(36)
In the BSM, participants view two stimuli, one for each eye, against two backgrounds set to the same adaptation level. Superimposed on the backgrounds are a reference stimulus at 589 nm at a reference radiance level for one eye and a test stimulus of varying wavelengths and radiances for the other eye. The stimuli are arranged so that, when using binocular vision, they appear 12degrees off-axis, one on top of the other. The experimenters flash the stimuli and adjust the radiance of the test stimulus until the participant sees the two stimuli appear at the same time. Using this method, the experimenters can measure the comparative radiances needed to detect the two stimuli simultaneously. From these results, luminous efficiency for the stimuli for a number of background adaptation levels can be measured.(27)
The resulting mesopic luminous efficiency function requires an iterative process to calculate the mesopic luminous intensity of a source with respect to the V10(λ) and V′(λ). functions and the adaptation level (X) in the mesopic range. Detection time does not suffer from the same bias toward saturated colors that brightness matching does; the function is additive and can describe multichromatic light sources.(28,36) One major criticism of the X-model is that it was developed using data from a very limited number of participants.
Mesopic Optimization of Visual Efficiency (MOVE) Model:
Like the creators of the X‑model, the researchers who developed the MOVE model wanted a practical model for mesopic vision designed with realistic nighttime driving in mind and based on the existing luminous efficiency functions. They defined a set of common experimental parameters and, as a consortium, conducted a large number of experiments based on contrast detection threshold, reaction time, and target recognition.(35,37)
Like the X-model, the resulting luminous efficiency function uses V′(λ) and x, a factor defining the adaptation of the eye-the region in the mesoic range where luminous efficiency is calculated. Unlike the X-model, it uses V(λ) and not V10(λ), because the researchers found that differences between the two were small, and using the more-common V(λ) was more practical.(37,38) The MOVE model also incorporates the S/P ratio of the light sources, and the luminance and spectrum of the background.(38) The MOVE model accurately predicted luminous efficiency for both off-axis tasks and tasks with multichromatic light but did not accurately predict luminous efficiency for narrow-bandwidth targets or on-axis tasks with monochromatic light at 0.01 cd/m2 (0.03 fL). These latter conditions are rarely encountered in nighttime driving.(37)
Problems With Models of Mesopic Vision:
Lighting designers have criticized both the X-model and the MOVE model for incorrectly placing the transition point from mesopic to photopic ranges. For the X-model, the transition occurs at 0.6 cd/m2 (0.18 fL); in the MOVE model, it falls at 10cd/m2 (2.9 fL). In practice, many lighting experts assume it falls somewhere in between.(39) Therefore, Viikari and Ekrias decided to test those models, alongside a modified version of the MOVE model with a transition at 5 cd/m2 (1.5 fL), using data from three previous experiments.(39) They found the modified MOVE model was the most accurate in predicting the experimental results in 9 of 17test cases. The original MOVE model was the most accurate in another seven cases, and the X-model was the most accurate in one case. The fact that no single model stood apart as predicting performance under all conditions indicates that more research is needed.
Another example of mixed results using different models of mesopic vision stemmed from research on lighting type and level and pedestrian visibility.(40) Results indicated HPS lighting outperformed metal halide (MH) lighting for a black-clad pedestrian but not for a blue-clad pedestrian. The pedestrians were likely detected foveally (where V(λ) accurately predicts performance), so mesopic effects, including the benefit of broader-spectrum sources, would not be as obvious. Experiments testing off-axis detection are more likely to produce mesopic effects.
Raphael and Leibenfer used a projector-based simulator to project a roadway and targets at 2, 6, 10, and 14 degrees off-axis with a range of background luminances and target contrasts.(41) They found that for targets near the fovea, V(λ) more accurately predicted the threshold contrast than mesopic models (including the X-model and the MOVE model), but for the 10- and 14-degree targets, the mesopic models predicted the contrast threshold better than photopic luminance.
CIE Recommended System for Mesopic Photometry Based on Visual Performance: (1)
Because in some aspects both the X-model and the MOVE-model can be considered to represent two extreme ends of a single system, the CIE Recommended System for Mesopic Photometry Based on Visual Performance adopted an intermediate system that operates in a region between the X-model and the MOVE model.(1) The objective of the recommended system was not only to make it widely applicable but also to increase the weight given to achromatic tasks. Two intermediate models were considered, with upper and lower luminance limits of 3 cd/m2 (0.88 fL) – 0.01 cd/m2 (0.003 fL) and 5 cd/m2 (1.5 fL) – 0.005 cd/m2 (0.00015 fL), respectively. After extensive testing, CIE recommended the intermediate system with an upper luminance limit of 5 cd/m2 (1.5 fL) and lower luminance limit of 0.005 cd/m2 (0.00015 fL) as the recommended system for mesopic photometry. It takes the form shown in figure 5.
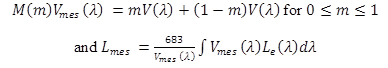
Figure 5. Equation. CIE formula for calculating mesopic spectral sensitivity.
Where:
M(x) = A normalizing function such that Vmes(λ) attains a maximum value of 1.
Vmes(λ0) = Value of Vmes(λ) at 555nm.
Lmes = Mesopic luminance.
Le(λ) = Spectral radiance in W.m-2sr-1nm-1.
if Lmes ≥ = 5.0 cd·m-2, then m = 1.
if Lmes = ≤ 0.0005 cd·m-2, then m = 0.
if 0.005 cd·m-2 < Lmes < 5 cd·m-2 then m = 0.3334.log Lmes + 0.767.
It should be noted that the recommended system does not correlate well with visual performance when recognition of color is important, when the target has a very narrow SPD, or when assessing brightness in the mesopic region.
Applying Models of Mesopic Vision to Roadway Lighting
Most nighttime driving occurs in the mesopic region, where the eye is more sensitive to blue light than photopic luminance, the standard for lighting design, would predict.(28,38) Because they are more efficient, broad-spectrum sources can be dimmer—consuming less energy while providing the same safety benefit—so those results are promising for energy savings. However, models of mesopic vision incorporated into CIE Recommended System for Mesopic Photometry Based on Visual Performance, including the MOVE model, were produced using laboratory data and must be further validated in roadway conditions before they can be fully applied to roadway lighting design.(1) Furthermore, broader-spectrum sources might be more efficient because they provide color information, or because they are better suited to mesopic vision. Experiments investigating mesopic vision and roadway lighting are described here and are the foundation for the work performed in this project.
X-Model Testing:
As part of the team that created the X-model, Bullough and Rea described a number of studies examining roadway lighting.(28) A test-track study found that reaction times with MH lighting were shorter than those with HPS lighting for peripheral targets, that headlamps had no effect on target detection for targets 15 and 23 degrees off-axis, and that glare reduced reaction time.(42) Another study, using a roadway lighting simulation with MH lamps (S/P ratio = 1.63) and HPS lamps (S/P ratio = 0.64), found that for foveal-target detection, participants had similar reaction times with the two lighting types.(43) However, for off-axis detection, reaction times with HPS lighting were slower than those for MH lighting, especially at lower light levels. To obtain similar reaction times, the HPS lighting had to be about 10 times as bright as the MH lighting, a ratio far greater than the ratio of S/P ratios of the lighting types (1.63:0.64 ≈ 2.5:1) would predict. Therefore, a comparison of the V(λ) and V′(λ) functions, on which S/P ratios are based, does not describe visual performance for off-axis detection in the mesopic range.(43) Two simulator studies found that HPS lighting needed to be much brighter than MH lighting, and brighter than the ratio of S/P ratios would suggest, to get the same target-detection performance.(44,45) Bullough and Rea concluded that, while photopic models accurately predict foveal detection and driving performance in the mesopic range for multiple lighting types, the S/P ratios underestimate MH performance for peripheral object detection - an important task in driving - and that the X-model is more accurate than using V(λ) and V'(λ) alone.(28) They recommended that roadway lighting should be designed with peripheral tasks in mind and to take a systems approach that accounts for headlamps, roadway lighting, and the cognitive demands of nighttime. Research into energy savings has acknowledged the importance of more accurate models of mesopic vision and recommends using MH lighting over HPS lighting based on the X-model and to use the newer models of mesopic visual performance.(46,47)
MOVE Model Testing:
The MOVE model has also been applied to roadway lighting. Eloholma and Halonen measured the photopic luminance of HPS and MH lighting with identical wattages and took background luminance measurements for selected areas of the roadway.(38) They found that the photopic luminance of MH lighting was lower than its MOVE-calculated mesopic luminance and that the photopic luminance of HPS lighting was higher than its MOVE-calculated mesopic luminance. The result was similar to that of the X-model testing: MH lighting performed better than HPS lighting in the mesopic range—more so than predicted by their S/P ratios alone—and MH lighting is more efficient than HPS lighting in the mesopic range.(38) Other experiments showed that both MH and LED lighting enable better roadside object detection than more common narrow-spectrum sources, like HPS lighting. (See references 19, 20, 22, and 23.)
As discussed previously, roadways are illuminated for nighttime driving with vehicle headlights and, on many roads, with overhead roadway lights. These different light sources have a combinative effect on roadway visibility. Several components affect this visibility in the roadway, as discussed in the following subsections.
Driving involves object detection, which in turn relies on detection of motion, luminance contrast, and color contrast. Some aspects of driving require higher acuity, such as reading signs or differentiating between similar objects. Object detection and categorization affects driver behavior; the difference between a tire tread and a pothole, or a pedestrian and a fixed structure, or a small animal and highway debris, are all significant in terms of driver reaction. Other aspects of driving, such as maintaining lane position, instead rely on peripheral vision and can be accomplished with lower acuity.
For nighttime driving, the lack of understanding of mesopic vision’s effect on visual acuity makes it difficult to predict driver’s visual behavior. Predicting this behavior at night is further complicated by changing lighting conditions as drivers pass under and away from roadway lighting fixtures and by glare from both luminaires and the headlamps of oncoming vehicles. This study examines visual behavior on a road with overhead lighting while driving a vehicle with headlamps.
As drivers’ eye age, changes occur in the optical density (OD) of the eye’s crystalline lens. With age, the lens becomes more yellow, reducing older persons’ ability to see color and color contrast.(48) Contrast contributes more to visibility than any other factor, so contrast sensitivity significantly affects hazard perception. That impact has been measured in driving studies; for example, in a study of older drivers, those with cataracts and poor contrast sensitivity had slower response times to traffic conflicts.(49) Another study measured the response time of younger and older drivers to roadside objects. Elderly participants were often surprised by the objects regardless of the lighting level, but younger participants identified the objects and avoided them.(50) The authors hypothesized that the age-related decrease in target detection was likely a result of diminished visual systems in older drivers, including diminished contrast sensitivity.
Aging affects older drivers’ response times and ability to steer, which may also be related to visual behavior. In a study by Wood et al., older drivers detected and recognized only 59 percent of pedestrians, whereas younger drivers recognized 94 percent of pedestrians.(51) Older drivers also recognized pedestrians much later than did younger drivers.(51) Another study found that older drivers’ steering accuracy in low-luminance settings was poorer than that of younger drivers.(52) However, Owens and Wood found that older drivers tended to drive more cautiously in low light than did younger drivers, showing they might be aware of, and compensating for, poorer vision.(50)
Despite the possibility that older drivers compensate for poorer vision, older drivers (ages 55+) comprised 16 percent of nighttime crash fatalities and nearly 25 percent of all crash-related fatalities, day and night.(53) Understanding how aging affects visual behavior, especially in mesopic night driving conditions, could increase traffic safety and reduce fatalities like those above. This study adds to that understanding.
Roadway and roadway-lighting design address increasing the visibility of roads and roadway objects to drivers. Contrast is a key component of visibility because the amount of contrast an object has is often directly related to how well it can be seen. There are two different types of contrast: luminance contrast, the comparative brightness of objects irrespective of color; and color contrast, the comparative difference in color between objects of the same or different luminances.
Contrast is directly related to visibility in static environments: the higher an object’s contrast, the more visible it is. However, because driving is dynamic—with overhead luminaires, moving headlamps, and potentially moving roadside objects—factors affecting visibility other than luminance contrast might come into play. Two of those factors, roadway and headlamp lighting, are investigated in this study and discussed in following sections.
When driving at night and using mesopic vision, a motorist’s ability to discern color varies with the amount of light available. Because the effect of color-contrast measurements on overall visibility changes with differing ambient lighting and vision conditions, most researchers measure luminance contrast, not color contrast, in night-driving studies.
Luminance Difference Thresholds
One of the key components of evaluating contrast is a model that quantifies the visibility of targets using the luminance difference threshold.(54) The calculation model uses variables that include target size, contrast, observer age, exposure time, eccentricity angle, adaptation, and distance to determine the visibility level (VL) of the target. A luminance difference is the difference between the luminance of a background and a target. A luminance difference threshold (ΔL) is the luminance difference at which the target is just perceived with a probability of 99.93 percent (ΔLth), the formula for which is shown in Figure 6:
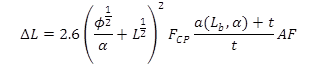
Figure 6. Equation. Luminance difference threshold.
Where:
ΔL = Threshold luminance difference.
Lb = Background luminance.
α is the target size in minutes of arc FCP is the Contrast Polarity Factor.
t = Observation time.
AF = Age factor.
φ and L are models of Ricco and Weber's Law
VL is a term introduced by Blackwell to better describe the level luminance difference must reach for a target to be rendered conspicuous. The formula for calculating VL is given in figure 7(54,55):
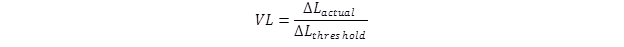
Figure 7. Equation. VL formula.
Where:
ΔLactual = Luminance difference between the target and the background.
ΔLTheshold = Calculated luminance difference between the target and the background.
Luminance contrast is the degree to which the luminance of a target distinguishes itself from the background luminance. The Weber contrast formula is commonly used because it accounts for contrast polarity. Positive contrast occurs when a light target is against a darker background; negative contrast occurs when a dark target is against a lighter background. Higher contrasts or high luminance differences do not always correlate with increased visibility. Therefore, by incorporating the variables included in the VL calculation, visibility becomes possible to quantify. The Weber contrast formula (figure 8) requires target luminance (Lt) and background luminance (Lb):
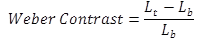
Figure 8. Equation. Formula for calculating Weber contrast.
VL expresses how much a target’s luminance exceeds the perception threshold and is a function of adaptation luminance. As cited by Adrian, VL values of 10 to 20 are considered to be safe traffic conditions.(54) The following sections describe the variables used for calculation in the VL model and how they are determined.
The visibility calculation considers the size of the target in the viewer’s visual field. A target can be as small as the wooden targets used in this project or as large as a pedestrian. Visual angle is used to describe object size because relative size in the visual field changes with distance from the object; the closer the object, the larger the visual angle.
The visual angle (α) can be calculated from the object's size, S, and its distance from the eye, D, from the viewer, as described in figure 9.
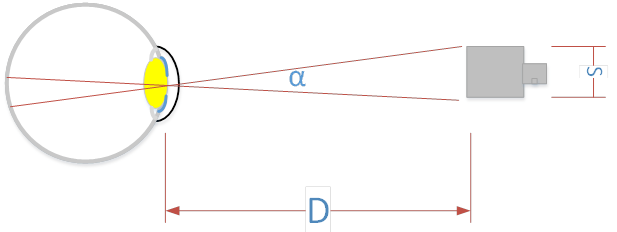
Figure 9. Diagram. Variables for calculating visual angle.
For small visual angles, such as the ones encountered when detecting the presence of small wooden targets on the roadside, the formula in figure 10 is used. To convert the visual angle from degrees to minutes of arc (MOA), α is multiplid by 60.
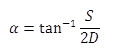
Figure 10. Equation. Formula for visual angle in degrees.
The contrast polarity factor (FCP), is a phenomenon explained by Aulhorn in 1964 as cited by Adrian.(54) Two figures with equal minimum luminance differences but different polarities, positive or negative, are not perceived the same way. A dark target on a light background (negative contrast) is detected sooner and with more distinguishable detail than is a light target on a dark background (positive contrast) with the same absolute value of minimum luminance difference. The luminance difference threshold for a target in negative contrast, ΔLneg, is calculated by multiplying the positive contrast, ΔLpos, by the contrast polarity factor, FCP, as described by the equation in figure 11.
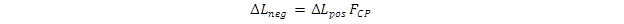
Figure 11. Equation. Calculation for negative contrast threshold.
The magnitude of the difference between the minimum positive and negative contrasts, FCP, required for object detection depends on the background and target size, as described by the equations in figure 12.
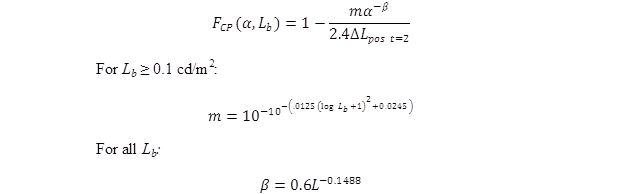
Figure 12. Equation. Calculation of the contrast polarity factor.
The model for visibility incorporates the increment of time that an observer views a target. For viewing times shorter than 0.2 s, a greater luminance difference threshold is needed for object detection. Typically a glance duration of 0.2 s is most commonly used for design criteria.(54)
Age is a critical factor in the visual perception of objects, especially in low light settings such as nighttime driving. As discussed above, the crystalline lens of the eye begins to yellow with increased age, limiting the amount and color of light entering the eye.(56–58) Adrian’s model accounts for age with two different age-factor calculations for two age groups: one for ages 23 to 64 and another for ages 64 to 75. The small target visibility model uses the following equations for the age groups listed in figure 13 and figure 14.
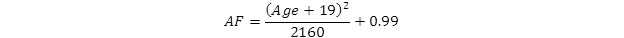
Figure 13. Equation. Age factor calculation for younger age group (23 to 64 years).
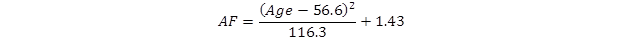
Figure 14. Equation. Age factor calculation for older age group (64 to 75 years).
Transient adaptation occurs when the eyes are in the process of adapting and have not established a steady state of adaptation. This adaptation process has two speeds: a quick neural process related to the photoreceptors and a slower physical process occurring when the pupil expands and constricts to adjust to the amount of light in the environment. During nighttime driving, light-level changes occur when a vehicle passes under and then beyond overhead-lighting fixtures, when the road surface and its reflectivity change, and when oncoming vehicles with headlamps approach. Adaptation typically occurs very quickly; however, if drivers’ eyes do not sufficiently adapt to the ambient lighting, their ability to detect contrast can be negatively affected.(59) Age can also negatively affect transient adaptation. The model for calculating VL with luminance threshold difference includes transient adaptation as an element of overall target visibility.
Eccentricity is defined as the angle, measured in degrees, along the horizontal axis of the visual field. Studies have shown that contrast sensitivity depends on several factors, including target size, eccentricity of the target, and the background luminance of the visual field. Increases in eccentricity are associated with increase in contrast threshold for targets of same size and background luminance.(60)
Momentary Peripheral Illuminators
In 2009, approximately 4,872 non-motor vehicle occupants (pedestrians, bicyclists, etc.) were fatally injured, and about 85 percent of those were pedestrians.(61) About 56 percent of the crashes occurred in rural areas, and 83 percent occurred where the speed limit was greater than 72 km/h (45 mi/h). It is likely that the absence of crosswalks, sidewalks, or shoulders on rural high-speed roads contributed to those crash fatalities.(61) In addition, approximately 51 percent of fatal pedestrian crashes occurred at dawn, dusk, or at night,(61) when visibility is more of an issue; most pedestrian crashes occur because vehicle drivers fail to see the pedestrians. Therefore, technology that helps drivers to see pedestrians on dark rural roads could contribute significantly to pedestrian safety.
An MPI system incorporates vehicle-based sensors that detect pedestrians with servo-actuated headlamps that pivot to highlight them, thus directing a driver’s attention to pedestrians. This section discusses a theoretical MPI system and its components, and proposes design criteria to ensure such a system is effective and successful.
Problems Detecting Pedestrians at Night
In the design of an MPI system, the following must be considered to establish the required specifications. Similarly, the experimental evaluation must account for these roadway visibility issues.
Peripheral Detection
When driving at night, drivers focus on the center of the roadway. However, pedestrians usually walk on the side of the road, where drivers must use peripheral vision to detect them. One of the limiting performance factors for the visibility of objects on the side of the road is that the human eye has low peripheral sensitivity and visual acuity; the eye’s sensitivity decreases as the object is detected farther away from the fovea.(18) Some research has found visual sensitivity plateaus between 8 and 30 degrees; other research in peripheral visibility found that target detection decreased with increasing angle, dropping off rapidly beyond 15 degrees. (See references 62–65.) In a road test, more than 80 percent of targets were not detected at a peripheral viewing angle of 17.5 degrees.(66) In all cases, peripheral object detection is poor, especially at greater angles. Motion of the object may help; however, most objects’ movement in the visual field is much slower than the flow of objects due to the motion of the vehicle. In addition, during nighttime driving, peripheral vision is mesopic, where the eye’s sensitivity to colors shifts toward blue as the environment’s luminance decreases (see Impact of Roadway Lighting section above), making accurately modeling visual performance problematic (see Models of Mesopic Vision section).
Headlamps
Headlamps are designed to help drivers see down the road and to minimize glare to oncoming traffic. Illuminating the oncoming lane causes glare to oncoming traffic, so headlamps are aimed to illuminate the roadway ahead of the vehicle and the right-hand side of the roadway.(18) Figure 15 shows a headlamp beam’s center, marked by “X,” and the beam pattern resulting from aiming the headlamp for the lower right-hand quadrant. Pedestrians usually appear in the lower left-hand and the upper right-hand quadrants, where the beam intensity tapers off.(18) If a car is far enough away from a pedestrian, the driver might use foveal vision to detect them, but vehicle headlamps might not illuminate the roadway to that distance. Therefore, by the time the headlamps illuminate a pedestrian, he or she is likely on the periphery of the visual field, making him or her difficult to see, and the driver may be too close to avoid a collision. This problem is compounded by roadside objects adding visual clutter and/or occluding the view of pedestrians.
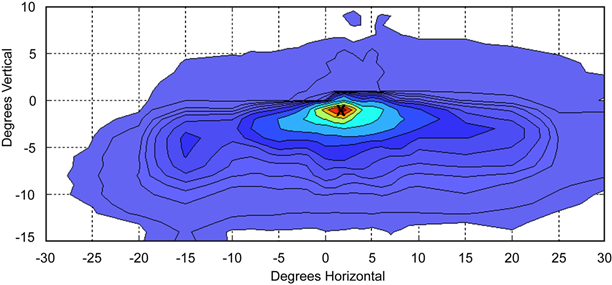
Figure 15. Graph. Headlamp beam pattern.(18)
One additional problem with headlamp design with respect to pedestrian detection is that drivers detect pedestrians using the contrast created when headlamps illuminate pedestrians against the background.(18) However, by design, headlamps are aimed low, illuminating both the pedestrian’s legs and the ground immediately surrounding them, thus decreasing contrast and hindering detection.(18) Increasing headlamp power mitigates that problem but increases glare to oncoming vehicles.
The headlamp system for the MPI system has two points of consideration: headlamp type and headlamp behavior.
Headlamp Type
During low lighting conditions, the headlamp should have an SPD efficient in the mesopic range and favor shorter wavelengths. High-intensity discharge (HID) lamps, tuned HID lamps, and LED lamps have all provided better off-axis visual performance than traditional headlamp types because of their SPDs. (See references 66 and 88–90.)
HID Headlamps:
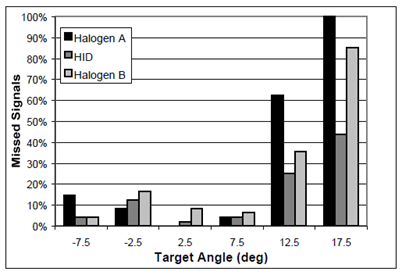
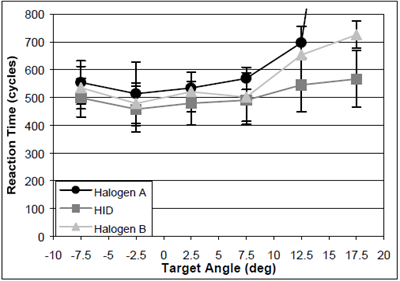
HID headlamps have higher luminous efficacy, higher color temperature, and longer life compared with more traditional halogen headlamps. These lamps are more intense in the beam’s periphery. When tested using off-axis targets, participants driving with HID headlamps have longer detection distances, fewer missed targets (figure 16), and shorter reaction times (figure 17) than participants driving with halogen headlamps.(66) HID headlamps enable better peripheral detection because of their higher color temperature, brighter area in front of the vehicle, and different light spectra. HID lamps have a wider spread of light than halogen lamps.
Reprinted with permission from SAE paper 2001-01-0298 Copyright ©2001 SAE International Further use and distribution is not permitted with permission from SAE.
Figure 16. Chart. Comparison between halogen and HID headlamps.(66)
Reprinted with permission from SAE paper 2001-01-0298 Copyright ©2001 SAE International Further use and distribution is not permitted with permission from SAE.
Figure 17. Graph. Comparison of reaction times between halogen and HID headlamps.(66)
Spectrally Tuned HID Headlamps:
Using special filters, HID headlamps can be tuned to emit a higher percentage of shorter wavelengths. Participants in a vehicle with tuned HID headlamps detected off-axis targets with shorter reaction times and fewer missed detections than those with regular HID headlamps.(88) (See figure 18.) A major limitation of the study was that the test vehicle was stationary; visual performance of drivers in moving vehicles with tuned HID headlamps should be further studied.
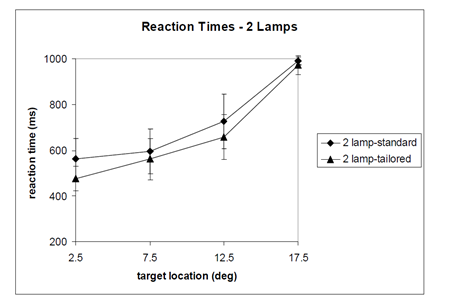
Source: Van Derlofske, J.F., Bullough, J.D., and Gribbin, C.
Figure 18. Graph. Reaction times with different HID headlamp types.(88)
LED Headlamps:
The use of LEDs is rapidly increasing in automotive headlamps. They have a longer life cycle, lower power requirements, and different spectra than HID lamps. In 2008, the Audi® R8 was the first car to have full LED headlamps, incorporating 54 high-performance LEDs.(91)
Researchers at the Lighting Research Center in Troy, NY, investigated the spectral distributions of 17 white LEDs used in headlamps. The S/P ratios of three white LEDs were found to be similar to or greater than a tuned HID headlamp, indicating that LED headlamps should permit drivers to see off-axis targets as effectively as tuned HID headlamps.(64)
Headlamp System Configuration
Typical headlamps are stationary and aimed down the road, where pedestrians are less likely to be detected. The headlamp portion of an MPI system would have two sets of headlamps, onestationary and the other directed by the MPI system controller to highlight pedestrians and roadway objects, increasing the probability of detection.
The MPI headlamps could be installed at a fixed angle with respect to the vehicle and flash momentarily as the car approaches a pedestrian. Alternately, the headlamps could be controlled by a servo and thus swivel and track the pedestrian as the vehicle moves down the road. These options are shown in figure 19. Both technologies require the MPI system to identify and track the pedestrian and then calculate the pedestrian’s position with respect to the vehicle.
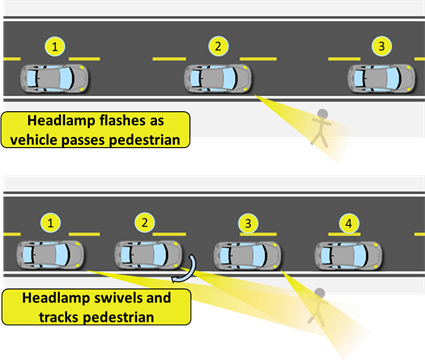
Figure 19. Diagram. MPI headlamp illuminating pedestrian by flashing on and swiveling.
Potential issues in tracking and illuminating pedestrians include deciding which type of headlamp to use, determining how long it is safe to illuminate a pedestrian and how to track and illuminate multiple pedestrians, and ensuring pedestrians are comfortable with the system. Research on MPI systems should determine which approach is best for pedestrian detection, pedestrian comfort, multiple-pedestrian tracking, and avoiding driver distraction.
Specification Development For an MPI system
As part of the development of the background for this project, the specifications of a functioning MPI system need to be developed.
Conceptual Design of an MPI System
An MPI system would overcome limitations in human vision and vehicle headlamp design by automatically detecting pedestrians and using side-aimed headlamps that illuminate the pedestrian in sufficient time for the driver to react. MPI headlamp light would be efficient in activating the eye’s photoreceptors in the mesopic range and not produce glare for oncoming drivers.
Such a system requires two primary components: a detection system and a lighting system. A conceptual design for one version of an MPI system is shown in figure 20. That system uses vision-based detection that enters pedestrian locations into a control system, which activates swiveling headlamps. Those and other detection and lighting systems are discussed in this section.
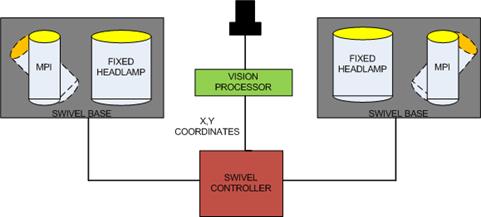
Figure 20. Diagram. Conceptual design of an MPI system.
An ideal pedestrian collision warning system would detect a pedestrian and the pedestrian’s position in time for the headlamp control system and headlamps to illuminate them. The detection system would need to have a low false-positive rate because drivers would not continue to pay attention to a system with a high false-positive rate. Prior research in pedestrian detection points to three commonly used sensor types, described in this section: vision-based sensors, infrared sensors, and sensors based on time of flight (TOF), such as radar and laser scanners.(67–69)
Vision-Based Sensors
Vision-based sensors detect high-resolution information from the environment, extract shapes from that information, and compare the shapes with a large sample of example images. If a shape matches an image of a pedestrian, a pedestrian is detected.
Extracting shapes from a complex visual environment can be accomplished in a variety of ways. Edge tracking and motion estimating, active frame subtraction, texture property analysis, are some possible approaches.(70–72) Other promising approaches analyze image intensity and motion information, leg symmetry, motion analysis and parallax, or use stereo matching.(73–75) Systems could also be trainable.(72,76) There are a large number of approaches for vision-based systems, but all are limited by darkness, where objects and background have no luminance contrast, and are also negatively affected by glare.
Thermal Infrared Sensors
Thermal infrared sensors detect human body heat and are effective when vision-based systems are not—at night—when the environment is cooler than human skin. A number of researchers have used thermal infrared sensors to detect and track pedestrians. Systems can use a single camera or stereo cameras, and detect pedestrians using size and aspect ratio, profile and contrast, and pedestrian contour. (See references 77–81.) Other systems use head detection, comparative motion of the pedestrian and background and relative motion of the vehicle and pedestrian.(78,82) One system even detected pedestrians and warned drivers.(82) Although thermal infrared sensors work in the dark, they are less effective in poor and hot weather.
TOF Sensors
TOF systems include radar and laser systems. They scan the environment, collect reflected radiation, and estimate the relative velocity of nearby objects based on the differences in time it takes for reflected radiation to arrive back at the sensor. TOF systems can be used to select objects of interest in the environment for further vision processing, reducing the computational load on the vision portion of the system.(83) They could also process data from a TOF system and an infrared system in parallel.(84)
Vision-based and infrared sensors provide high-resolution information about a captured scene. This high level of information comes at the expense of the amount of processing and computation. TOF sensors locate objects accurately, but their resolution is limited. Systems using both TOF and vision and/or infrared data would be effective in a variety of conditions but can be very expensive.
Pedestrian-Detection Algorithms
Vision-based, infrared-based, and TOF systems all require an algorithm to process the incoming data and determine whether a pedestrian is present. Despite the variation in detection technology, the detection algorithms are similar, with the basic algorithm structure shown in figure 21.(67)

Figure 21. Diagram. General structure of a pedestrian-detection system.(67)
This algorithm begins by hypothesizing that an object in the field of view is an object of interest and then validates whether or not the object in the field of view is actually an object of interest. The system then monitors the input from the sensors to further validate the hypothesis and tracks validated objects of interest. Using tracking information, the system calculates whether or not a collision is imminent. If a collision is imminent, the tracking information is forwarded to the MPI illuminator, which lights up the object of interest. If not, the system continues monitoring and tracking objects of interest.
Pedestrian-Detection System Development
DaimlerChrysler developed and tested the PROTECTOR system in traffic conditions.(85) The system detects pedestrians, estimates trajectories, assesses collision risk, and warns drivers. Although its performance was promising, PROTECTOR requires more research and development before it is implemented. Volvo also developed a pedestrian-detection system for the S60, using radar and a camera mounted on the front of the car to detect pedestrians and other objects.(86) It can detect pedestrians 0.8 m (32 inches) and taller, and, if a collision is imminent, it will alert the driver and automatically brake. Mobileye® technology has been used by automakers such as BMW, Volvo, and General Motors, and Mobileye® has developed several technologies for detecting pedestrians.(87) Mobileye® systems use a monocular approach and advanced spatiotemporal classification techniques based on machine learning, where the system is trained with static and dynamic information. This Mobileye® system does not, however, function in the dark.
Pedestrian-Detection System Requirements
Based on previous work, the pedestrian-detection portion of an MPI system should do the following: