U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-15-047 Date: August 2015 |
Publication Number: FHWA-HRT-15-047 Date: August 2015 |
This experiment was designed to investigate the applicability of the CIE Recommended System for Mesopic Photometry, described in chapter 2, to nighttime roadway conditions.(1) It also investigated the relationship between peripheral visual performance and the SPD of overhead-lighting sources in the mesopic range, in both static (parked) and dynamic (driving) conditions. To that end, three types of overhead lighting with different spectral distributions were used: 2,100-K HPS, 3,500-K LED, and 6,000-K LED. The level of the overhead lighting was chosen based on the adaptation luminance at the roadway. All adaptation luminance levels fell in the mesopic range, and all were the same among the different lighting types. The overhead lighting was used in combination with two pavement types—darker asphalt and lighter concrete—so the same level for an overhead-lighting type produced two different adaptation luminance levels, depending on pavement type. The experiment used five adaptation luminances for each lighting type, one of which was the same between asphalt and concrete. Three different off-axis target locations were used because research indicated that overhead-lighting sources whose spectral distributions favored the sensitivity of the rods had better off-axis performance.(20,21)
This experiment included two portions, one static and one dynamic. The static portion of the experiment was similar to laboratory and simulator studies on mesopic vision but was performed in a stationary vehicle on the roadway. Participants sat behind the steering wheel of the test vehicle and fixated on the center of the roadway while researchers adjusted the contrast of off-axis targets on the shoulder. The dependent variable was the threshold luminance contrast or contrast threshold at which the participant first saw the target. In the dynamic portion of the experiment, participants drove down the road and were instructed to fixate on the roadway and use peripheral vision to detect the targets. Targets at different eccentricities and contrasts were presented, and participant detection distances were measured. The static experiment used a fixed geometry setup, whereas the dynamic experiment used a nonfixed geometry setup.
Target color was not included in this experiment, because the experiment focused on the effects of overhead-lighting configuration, eccentricity, and adaptation luminance rather than effects of object color on mesopic visibility. For the same reason, vehicle headlamps were not used for this experiment, isolating the effects of overhead lighting on mesopic vision.
The purpose of the mesopic modeling experiment was to evaluate the following:
For the static portion, a 2 by 3 by 5 by 3 mixed-factors experiment was designed to investigate the effects of age, overhead-lighting type, adaptation luminance, and eccentricity on the threshold contrast where participants first detected a target.
For the dynamic portion, a 2 by 3 by 5 by 3 by 2 mixed-factors experiment was designed to investigate the effects of age, overhead-lighting type, adaptation luminance, eccentricity, target light intensity, and vehicle speed on target detection distance.
Participants of two age groups were exposed to all combinations of factors for the static experiment. The dynamic experiment was a partial factorial experimental design with all second-order interactions and one third-order interaction. Experimental variables are listed in table 27 through table 29.
Table 27. Mesopic modeling experiment—independent variables and values.
Independent Variable |
Used In Static |
Used In Dynamic |
Values |
| Age | Yes |
Yes |
Younger (25–35), Older (65+) |
| Overhead-Lighting Type | Yes |
Yes |
6,000-K LED (S/P 1.82), 3,500-K LED (S/P 1.31), 2100-K HPS (S/P 0.64) |
| Adaptation Luminance | Yes |
Yes |
0.07 cd/m2 (0.020 fL), 0.1 cd/m2 (0.03fL), 0.2 cd/m2 (0.06 fL), 0.3cd/m2 (0.09 fL), 0.5 cd/m2 (0.15 fL) |
| Eccentricity | Yes |
Yes |
6 degrees, 10 degrees, and 14 degrees |
| Speed | No |
Yes |
56 km/h (35 mi/h), 80 km/h (50 mi/h) |
Table 28. Mesopic modeling experiment—covariate and value/measurement method.
Covariate |
Used in Static |
Used in Dynamic |
Value/Measurement Method |
| Target Contrast | No |
Yes |
High and Low Contrast (Weber) |
Table 29. Mesopic modeling experiment—dependent variables and measurement method.
Dependent Variables |
Used in Static |
Used in Dynamic |
Measurement Method |
| Threshold Contrast | Yes |
No |
Weber contrast at which participant can first detect a target |
| Detection Distance | No |
Yes |
Distance at which participant can first detect a target |
Age
Participants were divided into the same age groups as previous experiments: younger (25–35 years old) (M = 28.4, SD = 3.2) and older (65 years old and older) (M = 67, SD = 1.5).
Overhead-Lighting Type
All three of the overhead-lighting systems were used.
Adaptation Luminance
Adaptation luminance was the photopic luminance viewed from inside the vehicle for a given combination of overhead-lighting level and pavement type. It was controlled for by adjusting the overhead-lighting levels for the three lighting types and two pavement types.
Overhead-Lighting Level:
Each lighting type was used at three intensity levels: low, medium, and high. Those lighting levels were adjusted so that the low, medium, and high intensity levels produced the same adaptation luminance inside the vehicle across the three lighting types, and so they were all in the mesopic range.
Pavement Type:
With the two pavement surfaces on the Smart Road, the pavement color and reflectance differed meaning that the same overhead-lighting level resulted in different adaptation luminances in the two sections. For this experiment, the overhead-lighting levels were adjusted so that the high overhead-lighting level on asphalt produced the same adaptation luminance as the medium overhead-lighting level on concrete. The result was five distinct adaptation luminances, shown in table 30.
Table 30. Mesopic modeling experiment—adaptation luminance by overhead-lighting level and pavement type.
Overhead-Lighting Level |
Luminance on Concrete (cd/m2 (fL)) |
Luminance on Asphalt (cd/m2 (fL)) |
| Low | 0.1113 (0.032) | 0.0716 (0.021) |
| Medium | 0.3535a (0.103) | 0.1987 (0.056) |
| High | 0.5385 (0.157) | 0.3535a (0.103) |
| aSame luminance. | ||
Eccentricity
Targets were placed at three angles with respect to the roadway: 6, 10, and 14degrees, as shown in figure 108. These angles were measured assuming the observer was at a vertical distance of 83m (272 ft) from the target location.
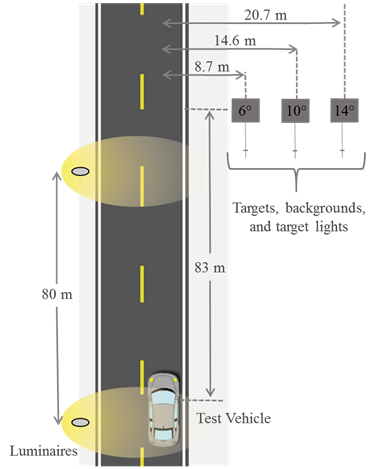
Figure 108. Diagram. Arrangement of target lights for static experiments on the Smart Road.
Speed
For the static portion of the experiment, the vehicle was parked in a specified location with respect to the targets, and speed was not an independent variable.
For the dynamic portion of the experiment, the vehicle traveled at 56 and 80 km/h (35 and 50mi/h).
Threshold Contrast
For the static portion of the experiment, the target’s light intensity was increased until the participant could just discern the target. At that point, threshold contrast of the target was calculated by first measuring the luminance of the target and background with a ProMetric® luminance camera inside the test vehicle and then by calculating the target’s Weber contrast from those measurements using the formula in figure 8. The threshold-detection measurements in this experiment measured supra-threshold contrast, where the participant definitely detected the target, whereas threshold contrast typically refers to the contrast at 50-percent detection probability.
Detection Distance
For the dynamic portion of the experiment, the detection distance was the dependent variable.
This experiment was conducted on the Smart Road using the same test vehicles as in previous experiments.
The target setup for this experiment was significantly different than those used in the other experiments. While the targets were the same gray targets as used in the previous experiments in this project, they were mounted on vertical posts, and their height was adjustable. Spotlights used to illuminate the targets were mounted on the same apparatus as the targets. The target illuminators were about 2.4 m (8 ft) from the targets and were also adjustable, so the experimenters could ensure the spotlight was centered on the target. The target lights were enclosed in light-tight cases, reducing scatter, so that the only light emitted was directed toward the target. The target stands and target lights were painted in a neutral camouflage pattern so they would not distract the participant drivers. The targets were illuminated using CREE® LED BR30 reflector spotlights rated at 650 lumens. A warm bulb (2,100 K) was used with the 3,500-K LED and 2,100-K HPS lighting, and a cool (5,000 K) bulb was used with the 6,000-K LED lighting.
The backgrounds were 0.91 by 1.2 m (3 by 4 ft) sheets of gray-painted plywood on gray-painted stands. The target-lighting apparatus were placed 4.6 m (15 ft) from the background. A target, a target light, and its background are illustrated in figure 109.

Figure 109. Photo. Mesopic modeling experiment—target, target light, and background.
Four sets of three targets, target lights, and backgrounds were set up alongside the Smart Road to create the three desired viewing angles at those four stations. The two stations in the asphalt section were named A1 and A2, and the two in the concrete section were named C1 and C2. All four stations were used in the dynamic portion of the experiment, but only stations A1 and C2 were used in the static portion of the experiment.
Participants were recruited and screened as described in chapter 3. A total of 18 participants performed the experiment. Nine were older, and nine were younger. Nine were female, and nine were male. Mean and standard deviation of participant age, visual acuity, mesopic visual acuity, low contrast visual acuity, and UFOV are listed in table 31.
Table 31. Mesopic modeling experiment participant characteristics.
Participant Characteristic |
Older Drivers Mean |
Older Drivers Standard Deviation |
Young Drivers Mean |
Younger Drivers Standard Deviation |
| Age | 70.4 |
6.3 |
30.5 |
3.2 |
| Visual Acuity | 20/24.2 |
8.8 |
20/19.4 |
8.8 |
| Mesopic Visual Acuity | 20/38.8 |
10.6 |
20/27.2 |
13.0 |
| Low Contrast Visual Acuity | 20/26.3 |
10.6 |
20/18.3 |
6.4 |
| UFOV | 1.55 |
0.73 |
1 |
0 |
Each participant attended three experimental sessions, one for each overhead-lighting type. Each session consisted of a static and dynamic portion, and two participants completed the experiment simultaneously.
Static
One participant was directed to park at the vehicle stopping point for station A1, and the other was directed to park at the vehicle stopping point for station C2. An in-vehicle experimenter asked the participant to focus on a cone placed on the roadway, so that the targets were visible in the participant’s peripheral vision. The researcher then slowly increased the intensity of the target light. When the participant was first able to see a target, he or she announced “target” and the researcher recorded the target light intensity. The procedure was repeated for targets at different viewing angles for a total of 24 times. At the end of the static portion of the experiment, the in-vehicle researchers notified other team members that they were finished, and the on-road researchers adjusted the equipment for the dynamic portion of the experiment.
Dynamic
Each participant performed 1 practice run and 12 experimental runs down and up the Smart Road for each overhead-lighting type during an experimental session. For the dynamic portion of the experiment, the on-road experimenters set the target light levels, target positions, and overhead-lighting level for each experimental run. The in-vehicle experimenters directed the participants to focus on the roadway while driving to encourage target detection in peripheral vision, ensured they drove at the correct speed, and recorded detections.
Static
A mixed-factors ANOVA was performed to determine how the independent variables affected threshold contrast. If results were significant, a Tukey’s HSD test was performed to determine which independent variables differed significantly from each other. In the graphs reporting Tukey’s HSD results, points sharing a letter are not significantly different from each other.
Dynamic
A partial mixed-factorial ANOVA was performed to determine how the independent variables affected detection distance.
In the static portion of the experiment, researchers varied the contrast of the off-axis targets, and participants told researchers when they could first see them. The threshold contrast, when the participant would first see the target, was the dependent variable.
The effect of the independent variables on threshold contrast is listed in table 32, with results described in detail after the table.
Table 32. Mesopic modeling experiment (static portion)—independent variables and their effect on threshold contrast.
Independent Variable(s) |
Degrees of Freedom |
F-value |
Pr>F |
| Age | 1 |
3.34 |
0.0832 |
| Overhead-Lighting Type | 2 |
18.55 |
< .0001a |
| Overhead-Lighting Type by Age | 2 |
3.18 |
0.0549 |
| Adaptation Luminance | 4 |
48.11 |
< .0001a |
| Adaptation Luminance by Age | 4 |
1.68 |
0.1765 |
| Eccentricity | 2 |
32.81 |
< .0001a |
| Eccentricity by Age | 2 |
3.04 |
0.0596 |
| Overhead-Lighting Type by Overhead-Lighting Level | 8 |
6.06 |
< .0001a |
| Overhead-Lighting Type by Eccentricity | 4 |
5.77 |
0.0005a |
| Adaptation Luminance by Eccentricity | 8 |
14.86 |
< .0001a |
| Overhead-Lighting Type by Adaptation Luminance by Eccentricity | 16 |
10.96 |
< .0001a |
| aSignficant at p < 0.05. Pr = Probability |
|||
Overhead-Lighting Type
Overhead-lighting type significantly affected threshold contrast, illustrated in figure 110, where points sharing a letter are not significantly different from each other. The 6,000-K LED lighting provided the lowest threshold contrast and the 2,100-K HPS lighting the highest threshold contrast. A Tukey’s HSD test found no statistical difference between the two LED lighting types, but HPS light differed significantly from both LED types.
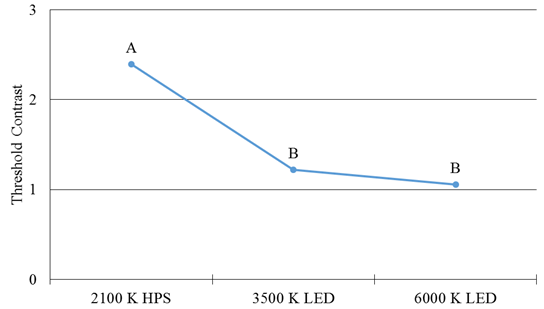
Figure 110. Graph. Mesopic modeling experiment (static portion)—threshold contrast by overhead-lighting type.
Adaptation Luminance
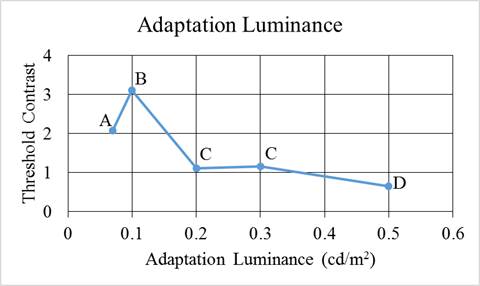
Adaptation luminance significantly affected threshold contrast, with, in general, lower adaptation levels requiring higher contrasts before the target was visible (see figure 111, where points sharing a letter are not significantly different from each other). A Tukey’s HSD test found all pairwise comparisons between adaptation luminances were significant, except the comparisons between 0.2 and 0.3 cd/m2 (0.06 and 0.09 fL) and 0.2 and 0.5 cd/m2 (0.06 and 0.15 fL). This could be because of a threshold effect where, if the luminance is above a certain level, increasing luminance no longer negatively affects contrast sensitivity. Adaptation luminance was also involved in statistically significant higher order interactions. This main effect could also be significantly influenced by the statistical significance of higher order interactions involving adaptation luminance.
1 cd/m2 = 0.3 fL
Figure 111. Graph. Mesopic modeling experiment (static portion)—threshold contrast by adaptation luminance.
Eccentricity
Eccentricity significantly affected threshold contrast, with targets farther off axis requiring greater contrast before they were visible, as shown in figure 112. Pairwise comparisons found that the threshold contrasts at all three eccentricities were significantly different from one another. That increase in threshold contrast cannot be attributed to loss due to probability summation because of the target locations (especially at 10 and 14 degrees) falling in the blind spot of the eyes. Binocular probability summation states that if the probability of detection by each eye is 50 percent (or 0.5), the probability that two eyes detect the signal when the target falls in the blind spot on one eye is now 0.5 + 0.5 – (0.5 x 0.5) = 0.75 or 75 percent (a 25-percent decrease compared with when the target is not in the blind spot of one eye). The threshold contrast at 10 degrees was 70-percent greater than that at 6 degrees, and at 14 degrees, it was 140-percent greater than that at 6 degrees. That is greater than the increase in threshold contrast predicted by binocular probability summation alone—25 percent.
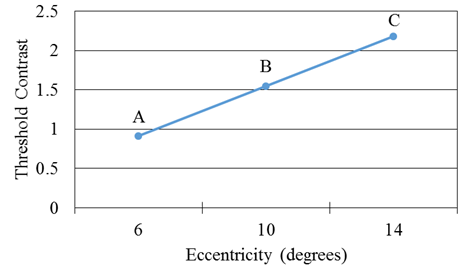
Figure 112. Graph. Mesopic modeling experiment (static portion)—threshold contrast by eccentricity.
Effect of Overhead-Lighting Type, Adaptation Luminance, and Eccentricity on Mesopic and Photopic Threshold Contrast
Luminance, as determined by the luminance meter used in this experiment, assumed measurements were taken in the photopic range. In the mesopic range, luminance calculations are different and account for the eye’s different mesopic spectral sensitivity. The above-threshold contrasts were calculated using luminance measurements as determined by the luminance meter, with no mesopic correction.
The mesopic correction factor is calculated by multiplying the photopic luminance by a correction factor based on the S/P ratio of the light source. The S/P ratio is the ratio of the lamp’s scotopic output to its photopic output, calculated using V(λ) and V'(λ) and describes the spectral sensitivity of the eye to the power distribution of a light source in mesopic conditions. The higher a lamp's S/P ratio, the better its light for peripheral detection in the mesopic region.(28,29) The mesopic output is calculated using the formula in figure 113 and figure 114, taken from the CIE Recommended System for Mesopic Photometry Based on Visual Performance.(1)
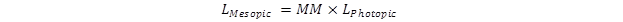
Figure 113. Equation. Formula for calculating mesopic output.
Where:
Lmesopic = Mesopic luminance.
MM = Mesopic multiplier from the CIE Recommended System for Mesopic Photometry Based on Visual Performance.(1)
LPhotopic = Photopic luminance.
Mesopic threshold contrasts were calculated by first calculating the mesopic luminance of the target and the mesopic luminance of the target’s background using the equation in figure 114:
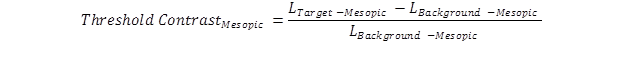
Figure 114. Equation. Formula for calculating mesopic threshold contrast.
Where:
LTarget-Mesopic = Mesopic luminance of the target.
LBackground-Mesopic = Mesopic luminance of the background.
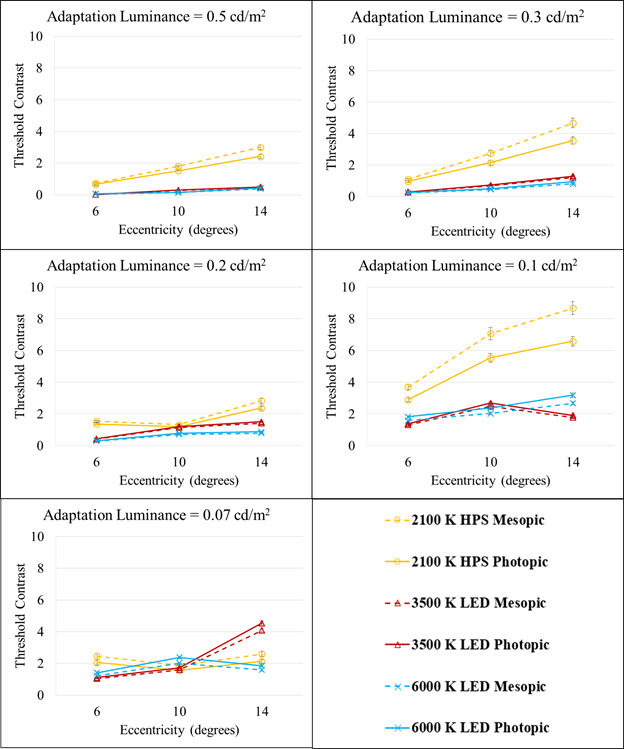
Threshold contrasts using photopic luminance values were compared with those using calculated mesopic luminance values to determine where the results diverge and which luminance calculation best predicts the results. Calculations were repeated for each adaptation luminance and are displayed by lighting type and eccentricity in figure 115.
1 cd/m2 = 0.3 fL
Figure 115. Graph. Mesopic modeling experiment (static portion)—threshold contrasts calculated with photopic and mesopic luminances for the three lighting types and three eccentricities.
From figure 115, it is clear that broad spectrum overhead-lighting types with higher S/P ratios (3,500-K LED and 6,000-K LED) had considerably lower off-axis threshold contrast values compared with narrow spectrum 2,100-K HPS lighting. The threshold contrasts were lower for LED lighting at all eccentricities and at four of the five adaptation luminances, showing that greater contrast was needed in HPS than LED lighting to see the same object.
Surprisingly, both threshold contrasts for HPS lighting were highest at 0.1 cd/m2 (0.03 fL) and not the dimmer 0.07 cd/m2 (0.020 fL) one would expect.
Photopic threshold contrasts for HPS were lower than the mesopic threshold contrasts. For LED lighting, the opposite was true.
In the dynamic portion of the experiment, participants drove with their eyes focused on the roadway, detecting the off-axis targets in their peripheral vision. Age, overhead-lighting type, adaptation luminance, eccentricity, speed, and target contrast were independent variables. A partial mixed-factors ANOVA was performed to determine how the independent variables affected detection distance.
The effect of the independent variables on detection distance is listed in table 33, with results described in detail after the table.
Table 33. Mesopic modeling experiment (dynamic portion)—independent variables and their effect on threshold contrast.
Factor(s) |
Degrees of Freedom |
F-value |
Pr > F |
| Age | 1 |
1.2 |
0.2898 |
| Overhead-Lighting Type | 2 |
0.18 |
0.8325 |
| Adaptation Luminance | 4 |
2.98 |
0.0263a |
| Eccentricity | 2 |
1.69 |
0.2014 |
| Speed | 1 |
0.23 |
0.6349 |
| Contrast | 1 |
0.87 |
0.3654 |
| Overhead-Lighting Type by Adaptation Luminance | 8 |
3.25 |
0.0027 |
| Overhead-Lighting Type by Eccentricity | 4 |
0.74 |
0.572 |
| Adaptation Luminance by Eccentricity | 8 |
2.73 |
0.0091a |
| Overhead-Lighting Type by Speed | 2 |
0.34 |
0.7174 |
| Adaptation Luminance by Speed | 4 |
2.29 |
0.0731a |
| Eccentricity by Speed | 2 |
3.55 |
0.0433a |
| Contrast by Overhead-Lighting Type | 2 |
4.09 |
0.0303a |
| Contrast by Adaptation Luminance | 4 |
1.35 |
0.2636 |
| Contrast by Eccentricity | 2 |
0.98 |
0.3904 |
| Contrast by Speed | 1 |
0.55 |
0.4711 |
| Overhead-Lighting Type by Adaptation Luminance by Eccentricity | 16 |
2.08 |
0.0164a |
| aSignficant at p < 0.05 or marginally significant at p < 0.1. Pr = Probability. |
|||
Only the main effect of adaptation luminance was significant. Four two-way interactions and a three-way interaction among overhead-lighting type, adaptation luminance, and eccentricity were also significant.
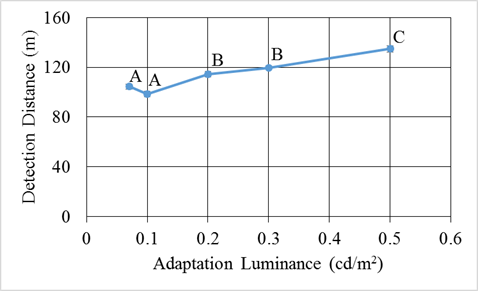
Adaptation Luminance
The effect of adaptation luminance on detection distance, plotted in figure 116, was significant. Points sharing a letter in the figure do not differ significantly from one another. Targets in the areas with the highest adaptation luminances were detected from farther away than those in areas with the lower adaptation luminances.
1 cd/m2 = 0.3 fL
1 m = 3.3 ft
Figure 116. Graph. Mesopic modeling experiment (dynamic portion)—detection distance by adaptation luminance.
Overhead-Lighting Type and Adaptation Luminance
The effect on detection distance of the interaction between overhead-lighting type and adaptation luminance was significant when all eccentricities were combined. There was no difference in the mean detection distance among the three overhead-lighting types at the highest and lowest adaptation luminance levels (0.5, 0.3, and 0.01 cd/m2 (0.15, 0.09, and 0.03 fL)). However, at the intermediate adaptation luminance levels (0.1 and 0.2 cd/m2 (0.03 and 0.06 fL)), detection distances were different across the different overhead-light types, as illustrated in figure 117. More information was extracted from these trends by including the eccentricity in these data, as described in the section Overhead Lighting Type, Adaptation Luminance, and Eccentricity.
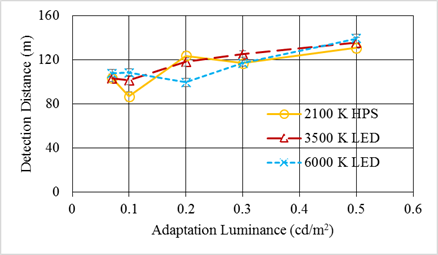
1 cd/m2 = 0.3 fL
1 m = 3.3 ft
Figure 117. Graph. Mesopic modeling experiment (dynamic portion)—effect of overhead-lighting type and adaptation luminance on detection distance.
Eccentricity and Speed
The effect on detection distance of the interaction between eccentricity and speed was significant. At both speeds, more eccentric targets were detected from farther away, as illustrated in figure 118. Also, objects were detected from farther away at the lower speed compared with the higher speed.
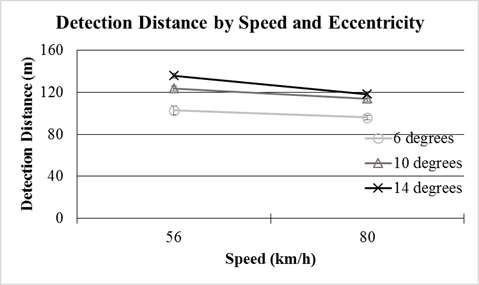
1 m = 3.3 ft
1 km/h = .62 mi/h
Figure 118. Chart. Mesopic modeling experiment (dynamic portion)—effect of eccentricity and speed on detection distance.
Adaptation Luminance and Eccentricity
The interaction between adaptation luminance and eccentricity was also significant. The detection distance was longer for higher adaptation luminances and targets at greater eccentricities. The 6-degree eccentricity target had the lowest mean detection distance across all the adaptation luminances. The 10- and 14-degree targets had higher detection distances at every adaptation luminance. An increase in adaptation luminance was also associated with an increase in the detection distance. The results, illustrated in figure 119, also show that an increase in the adaptation luminance significantly affected the detection distances of objects at higher eccentricities. The 14-degree target at 0.07 cd/m2 (0.020 fL) had a higher detection distance than those at the other two angles, 6 and 10 degrees.
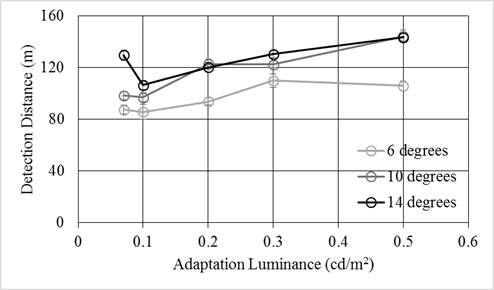
1 cd/m2 = 0.3 fL
1 m = 3.3 ft
Figure 119. Graph. Mesopic modeling experiment (dynamic portion)—effect of adaptation luminance and eccentricity on detection distance.
Overhead-Lighting Type, Adaptation Luminance, and Eccentricity
Mean detection distances increased as adaptation luminance increased, and different light sources had longer detection distances at different adaptation luminances, as shown in figure 120. An increase in eccentricity corresponded to both an increase in detection distance and a decrease in the difference between detection distances among the overhead-lighting types. At a 6-degree eccentricity, the 2,100-K HPS lighting resulted in had longer detection distances at adaptation luminances of 0.5 and 0.2 cd/m2 (0.15 and 0.06 fL), but the three lighting types had similar detection distances at adaptation luminances of 0.1 and 0.3 cd/m2 (0.03 and 0.09 fL). The 6,000-K LED overhead lighting had shorter detection distances than the other lighting types at the 6-degree eccentricity at all adaptation luminance levels. At the 10-degree eccentricity, both of the LED overhead-lighting types had longer detection distances than HPS lighting at every adaptation luminance. However, that trend did not occur at the 14-degree eccentricity, where no lighting type had longer detection distances at all adaptation luminances.
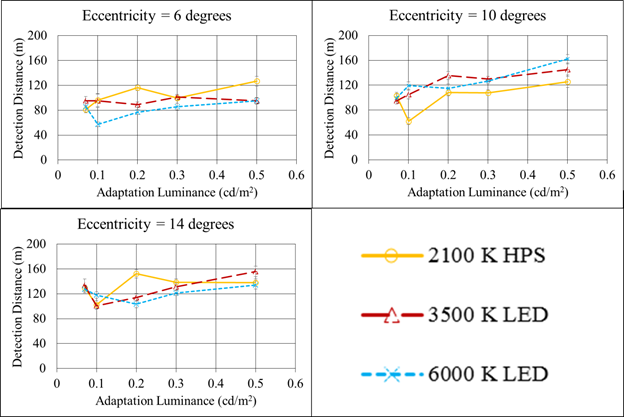
1 cd/m2 = 0.3 fL
1 m = 3.3 ft
Figure 120. Graph. Mesopic modeling experiment (dynamic portion)—effect of overhead-lighting type, adaptation luminance, and eccentricity on detection distance.
This research effort focused on application of the CIE Recommended System for Mesopic Photometry Based on Visual Performance to realistic nighttime roadway conditions and directly addressed the project objective to evaluate the effectiveness of mesopic models in a driving environment.(1) A two-pronged approach was used. First, a static experiment was conducted to replicate fixed geometry laboratory tests to understand the effects of overhead-lighting type, adaptation luminance, and eccentricity on peripheral threshold contrasts of participants of different age groups. Second, a dynamic experiment was performed in which the same participants drove at two different speeds to detect targets under the same conditions of overhead lighting, adaptation luminance, and eccentricity. The dynamic experiment helps answer questions regarding how nonfixed geometry affects peripheral visual performance; as in any driving task, the objects on the periphery of the road subtend different angles at different instances. The analysis of the static and dynamic experiments provided insights into not only the applicability of the CIE recommended mesopic system but also how overhead-lighting sources, adaptation luminance, and eccentricities affected peripheral visual performance.
The results showed that both LED overhead-lighting sources showed significantly lower threshold contrasts compared with the HPS source. Participants found it more difficult to detect the targets in HPS lighting and required higher contrast to do so, likely because HPS spectral distribution does not align with the eye’s sensitivity in the mesopic range. A light source with higher S/P ratios, such as the LED light sources tested, produces more light in the wavelengths where the rod photoreceptors are more sensitive and lowers the peripheral contrast threshold of the targets. These results align with previous research, which showed that light sources with higher S/P ratios had better peripheral visual performance. (See references 20, 21, 28, 42, and 44.)
An increase in adaptation luminance is also associated with a decrease in the threshold contrast. These results are in agreement with other studies that indicated that an increase in adaptation luminance reduces threshold contrast.(41) Both the LED light sources required lower contrasts to detect peripheral targets compared with the HPS source, as shown in figure 121. Again, this can be attributed to LED light sources producing light in the wavelengths that make the rods more sensitive. An increase in the eccentricity of the target was associated with an increase in the threshold contrast. These results align with previous research that found visual acuity outside the fovea decreases with eccentricity.(60)
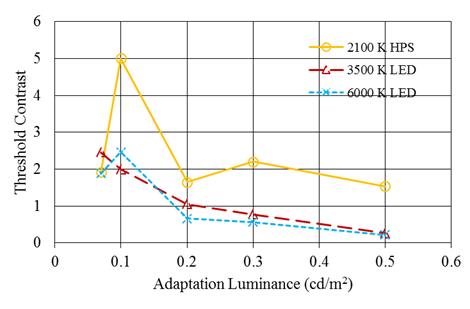
1 cd/m2 = 0.3 fL
Figure 121. Graph. Mesopic modeling experiment (static portion)—threshold contrasts of targets under different overhead-lighting sources at different adaptation luminances.
Comparison of Mesopic and Photopic Threshold Contrasts
The mesopic threshold contrasts were calculated from the mesopic luminances of the targets and their backgrounds under different overhead-lighting types and adaptation luminances and at threedifferent eccentricities. These mesopic threshold contrasts were compared with the photopic contrasts to see how they varied. The difference between photopic and mesopic threshold contrasts for target detection for the 2,100-K HPS lighting was largest at 0.1 cd/m2 (0.03 fL) and higher eccentricities. For HPS lighting, the difference in photopic and mesopic threshold contrasts decreased as eccentricity decreased and decreased as adaptation luminance increased. For LED lighting, the differences in photopic and mesopic threshold contrasts were smaller than those for HPS lighting but also became slightly greater for lower luminance levels, mirroring the trend in HPS lighting. This shows that for HPS lighting, photopic luminance measurements may be the least accurate, especially at low light levels. For both lighting types, photopic threshold contrasts were more accurate at higher luminances.
The unexpectedly low threshold contrast at 0.07 cd/m2 (0.020 fL) could be because at the far periphery, and at the lowest lighting level, the peripheral area of the retina was not adapted to the measured adaptation luminance. The adaptation levels for this study were calculated at the roadway surface, where the drivers were instructed to fixate. At the lowest levels of HPS lighting, the 10‑ and 14-degree locations were very dark, with a luminance approaching scotopic levels. The difference in adaptation levels between the fovea, where participants were looking at the brighter roadway, and 10 and 14 degrees in the periphery, where they detected the targets, meant the eye’s periphery was not adapted to the same level as the fovea. At the periphery, the eye was adapted to darker lighting levels, reducing the threshold contrast for those conditions.
CIE Recommended System for Mesopic Photometry
The CIE model for mesopic spectral sensitivity makes it possible to calculate the mesopic luminance when the photopic luminance and S/P ratio of the light source are known.(1) The outputs of the CIE model for mesopic spectral sensitivity are the mesopic luminance and the weighting factor for calculating the mesopic spectral luminous efficiency function from the photopic spectral luminous efficiency function V(λ) and scotopic spectral luminous efficiency function V′(λ).
An ideal model for mesopic spectral sensitivity would describe the mesopic luminances of the target and background (and therefore contrast) the same way for the light sources with different spectra; it would be independent of the lighting type’s color. The CIE model makes it possible to make the mesopic luminance independent of the spectrum of the light source. However, in figure 122 (which shows the mesopic luminances for the different overhead-lighting types calculated using the CIE model), the mesopic contrast was different for different light sources at the same adaptation luminance. Therefore, for this experiment, the CIE model did not accurately produce mesopic luminance, contrast, and threshold contrast values that were independent from the light-source spectra. The greatest difference was for HPS lighting. The CIE model performed very well for 6- and 10-degree eccentricities for both of the LED lighting types; the mesopic threshold contrast lines are very close to each other for different adaptation luminances, as shown in figure 122. However, at an eccentricity of 14 degrees and adaptation luminance of 0.07cd/m2 (0.020 fL), the predicted mesopic contrasts were very different from one another.
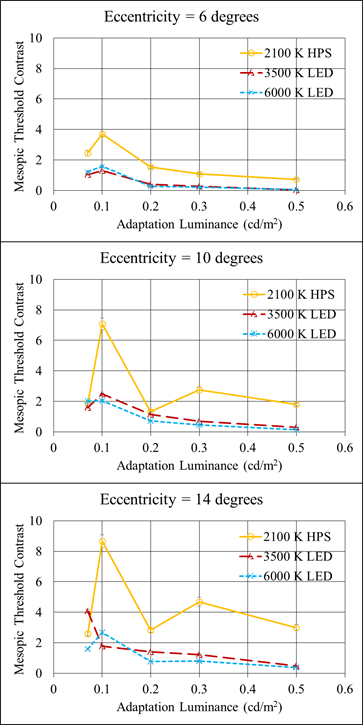
1 cd/m2 = 0.3 fL
Figure 122. Graph. Mesopic modeling experiment (static portion)—mesopic contrast thresholds as predicted by the CIE Mesopic Spectral Sensitivity Model.
Predicted Versus Actual Difference in Mesopic Luminances
The threshold contrasts in the HPS lighting were significantly different from both LED lighting types. This section compares the actual difference in the mesopic luminance (delta, expressed as a percentage) between the HPS lighting and both LED lighting types to the predicted difference (expressed as a percentage) in mesopic luminance from the CIE Recommended System for Mesopic Photometry Based on Visual Performance.(1)
For example, the difference between 2,100-K HPS and 6,000-K LED lighting is calculated in the following way (figure 123, from table 11 in CIE Recommended System for Mesopic Photometry Based on Visual Performance):
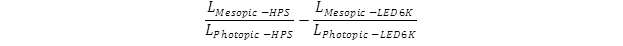
Figure 123. Equation. Formula for calculating the mesopic luminance difference between 2,100-K HPS and 6,000-K LED lighting.(1)
Where:
Lmesopic-HPS= Mesopic target luminance under 2,100-K HPS lighting.
LPhotopic-HPS= Photopic target luminance under 2,100-K HPS lighting.
LMesopic-LED6K= Mesopic target luminance under 6,000-K LED lighting.
LPhotopic-LED6K = Photopic target luminance under 6,000-K LED lighting.
For instance, the percentage difference in mesopic and photopic luminance for HPS lighting (S/P = 0.64) and LED 6,000-K lighting (S/P = 1.82) at 0.1 cd/m2 (0.03 fL) is -5 and +27percent, respectively. Therefore, the predicted difference is (-5 – 27) percent = -32 percent.
Figure 124 illustrates the difference in the calculated and predicted delta between the HPS and LED lighting types at each adaptation luminance for each eccentricity. The differences in the calculated and the predicted mesopic luminance between HPS lighting and both the LED lighting types at eccentricities of 6 and 10 degrees show the same trend from the lowest adaptation luminance to 0.2 cd/m2 (0.06 fL). The calculated difference evened out above this level. For the 14-degree eccentricity, the calculated deltas between the HPS and the LED lighting types were most similar at the lowest adaptation luminances. However, as the adaptation luminance increased, the predicted and calculated deltas diverged, with the greatest difference at 0.5 cd/m2 (0.15 fL). From this analysis, it is evident that the CIE model accurately predicted the mesopic luminances to about 0.2 cd/m2 (0.06 fL), up to 10-degree eccentricity off-axis. At higher adaptation luminances and eccentricities, the calculated delta between the HPS and LED lighting types evened out rather than decreased as the model predicted. The differences between calculated and predicted mesopic luminances increase with increasing eccentricity. Because the CIE model does not use eccentricity as an input parameter, the results for this study suggest that a mesopic model with eccentricity as an input parameter might predict the mesopic luminances more accurately.
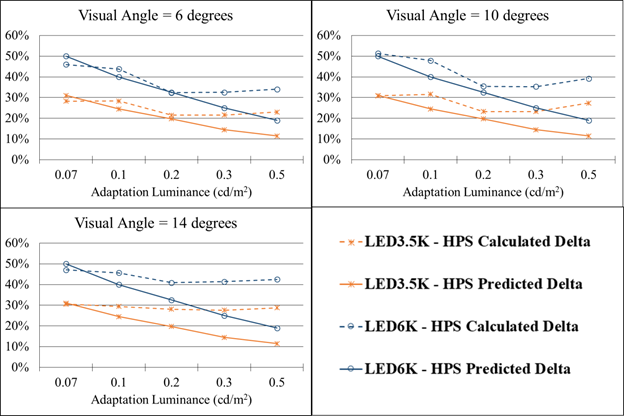
1 cd/m2 = 0.3 fL
Figure 124. Graph. Mesopic modeling experiment (static portion)—calculated versus predicted deltas (difference in mesopic luminance expressed as a percentage) between HPS lighting and each of the LED lighting types.
In the dynamic experiment, adaptation luminance significantly affected the distance at which peripheral targets were detected. An increase in the adaptation luminance resulted in an increase in the detection distance. An increase in the eccentricity was also associated with an increase in the detection distance. Unlike the results of the Akashi and Rea study, where the main effect of overhead-lighting type was significant with the metal halide light (higher S/P ratio) source eliciting shorter response times compared with HPS lighting for targets of eccentricity 15 and 23degrees, the current study did not show a significant main effect of overhead-lighting type.(42) However, there are some significant differences in experimental design between the two studies that could have contributed to the different results. For instance, Akashi and Rea’s study did not look at different adaptation luminances. Also, that study used a single vehicle speed, whereas the current study looked at multiple adaptation luminances and two different vehicle speeds. Overhead-lighting type alone did not significantly affect the detection distance of peripheral targets, which is surprising because it was anticipated that light sources with higher S/P ratios would result in significantly better peripheral visual performance. However, overhead-lighting source, along with adaptation luminance, had an effect on visual performance of peripheral targets. Overhead-lighting types with higher S/P ratios (the 3,500-K LED and 6,000-K LED lighting), had better peripheral visual performance for 10-degree off-axis targets. There were no clear trends regarding overhead-lighting type for the 6- and 14-degree off-axis targets.
For the HPS lighting at larger eccentricities (10 and 14 degrees), the mean detection distances at 0.07 cd/m2 (0.020 fL) were higher than those at 0.1 cd/m2 (0.03 fL). This phenomenon could be the result of differential adaptation of the fovea and the periphery of the eye. The adaptation luminances used in the study were measured at the surface of the roadway; the luminance level decreased as distances increased off-axis from the roadway. At a foveal adaptation luminance of 0.07 cd/m2 (0.020 fL) and an eccentricity of 14 degrees, the adaptation luminance of the periphery of the eye is much lower—possibly close to the lower end of the mesopic range—making the peripheral rod receptors more sensitive and increasing detection distances. That increased sensitivity in the periphery at low adaptation levels could have resulted in better performance at lower lighting levels. HPS was the only overhead-lighting type that displayed differential adaptation at 0.07cd/m2 (0.020) at 10 degrees of eccentricity. The low S/P ratio of the HPS lighting could have contributed to the longer detection distances at 0.1 cd/m2 (0.03 fL). Both LED lighting types have a higher S/P ratios (1.31 and 1.82), which could have made them perform better at this eccentricity for the same adaptation luminance.
The main effect of speed was not significant. However, the interaction between speed and eccentricity was significant. Figure 118 is repeated below as figure 125 for reference. Targets at higher eccentricities were detected at a greater distance at lower speeds than those at lower eccentricities and higher speeds. The target with 14-degree eccentricity at the 56 km/h (35 mi/h) had the highest mean detection distance (M = 139 m (456 ft)) and the target with 6-degree eccentricity at (80.47 km/h (50 mi/h) had the lowest mean detection distance (M = 95.9 m (315ft)). These results indicate that at higher speeds, drivers’ visual fields narrow, negatively affecting their ability to detect objects in their peripheral vision. These results align with existing research done using driving simulators where peripheral visual performance was poorer at higher speeds.(97) Because the higher order interactions of eccentricity and speed with either overhead-lighting type or adaptation luminance were not significant, neither overhead-lighting type nor adaptation luminance influenced the change in the size of the visual field caused by driving speed.
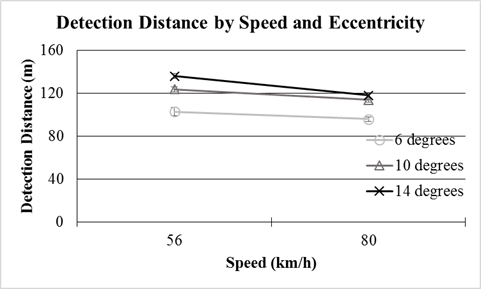
1 m = 3.3 ft
1 km/h = 0.62 mi/h
Figure 125. Graph. Mesopic modeling experiment (dynamic portion)—effect of eccentricity and speed on detection distance.
Transition From Static to Dynamic
Even though in the static (fixed geometry) experiments overhead-lighting type, adaptation luminance, eccentricity, and their interactions were all significant in the dynamic experiment (nonfixed geometry), only the main effect of adaptation luminance and the three-way interaction among overhead-lighting type, adaptation luminance, and eccentricity were significant. This shows that in dynamic conditions, unlike static conditions, overhead lighting alone does not contribute significantly to peripheral visual performance. In dynamic conditions, peripheral visual performance very much depends on factors such as adaptation luminance, eccentricity, and speed. Even though for 10-degree targets, the LED light sources had marginally better performance, this result could not be replicated at either 6- or 14-degree eccentricities. Overall, there were no clear trends in the dynamic experiment that indicate which overhead lighting source resulted in better peripheral visual performance. The only trend clearly evident from the dynamic experiment is the role of adaptation luminance in peripheral visual performance. The results indicate that increased adaptation luminance results in target detection from longer distances, thereby resulting in increased peripheral visual performance. The same result was also observed in the static experiment, where threshold contrasts were lower at higher adaptation luminances. These trends are clearly illustrated in figure 126.
In the static phase of the experiment, the threshold contrasts for the HPS overhead-lighting sources were significantly higher compared with the LED sources. Taking this information into consideration, it was expected that the HPS lighting would perform poorly in the dynamic experiment. From the previous discussion, it is clear the all three overhead-lighting sources had similar performance, with only marginal differences. These differences in peripheral visual performance are illustrated in figure 127.
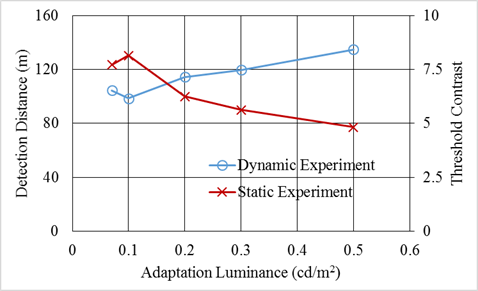
1 cd/m2 = 0.3 fL
1 m = 3.3 ft
Figure 126. Graph. Mesopic modeling experiment—peripheral visual performance in both static and dynamic experiments at different adaptation luminances.
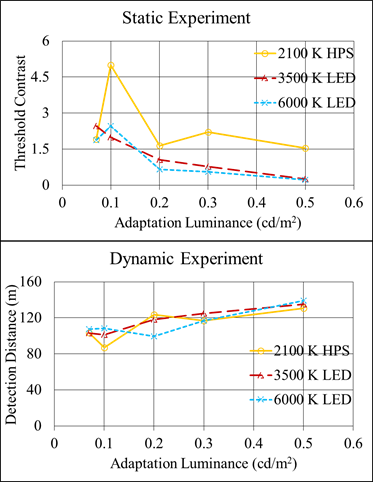
1 cd/m2 = 0.3 fL
Figure 127. Graph. Mesopic modeling experiment—peripheral visual performance of overhead lighting types at different adaptation luminances.
Age
The effect of age was not statistically significant either in the static experiment or in the dynamic experiment. This was interesting result, because it was expected that age would be a significant factor in peripheral visual performance. Because the average age of the older participants is 67years, it is also possible that the selected sample of older drivers was not old enough to see statistically significant changes, especially in peripheral contrast sensitivity. There were, however, differences in the threshold contrasts and detection distances of targets in both static and dynamic experiments; younger participants detected targets at lower threshold contrasts (MYoung = 1.27 m (4.17 ft) versus MOld = 1.81 m (5.94 ft)) and longer detection distances (MYoung = 122.58 m (402.17 ft) versus MOld = 109.91 m (360.60 ft)) compared with older participants. These differences were also not statistically significant.
The primary goal of this mesopic modeling experiment was to verify the applicability of the CIE Recommended System for Mesopic Photometry in naturalistic nighttime roadway situations, addressing the project objective of evaluating mesopic models in a driving environment.(1) The CIE Recommended System for Mesopic Photometry accurately predicted the mesopic luminances and contrasts for both the LED light sources at smaller eccentricities but not for the HPS light source. Differences between the mesopic and the photopic luminances of HPS lighting and both the LED overhead-lighting sources indicated that the calculated differences closely followed the predicted differences from 0.07 to 0.2 cd/m2 (0.020 to 0.06 fL). Beyond this range, the calculated differences leveled off, whereas the predicted values continued to decrease. The results show that the existing system does not take eccentricity into account, and the results show that the mesopic luminances calculated at greater eccentricities were less accurate. An ideal mesopic model should also use eccentricity as an input to accurately calculate mesopic luminances.
The secondary goal of the study was to assess the effect of an overhead lighting source’s spectrum on drivers’ peripheral visual performance in both static and dynamic conditions, addressing the project objective of evaluating the impact of spectra of overhead-lighting systems. In the static experiment, overhead-lighting type, adaptation luminance, and eccentricity significantly affected the threshold contrast at which participants were able to detect a target. Light sources with higher S/P ratios (3,500-K and 6,000-K LEDs) had lower threshold contrasts at detection in the periphery, compared with light sources with lower S/P ratios (2,100-K HPS), as suggested by existing research. An increase in eccentricity resulted in an increase in the threshold contrast. An increase in the adaptation luminance resulted in a decrease in the threshold contrast. In the dynamic experiment, peripheral visual performance was mainly affected by adaptation luminance. Increases in the adaptation luminance resulted in detection of objects from longer distances. Surprisingly, overhead-lighting type did not influence peripheral visual performance in the dynamic experiment. Targets with larger eccentricities and lower speeds were detected from longer distances, indicating that drivers’ visual fields narrow at higher speeds, which negatively affects peripheral visual performance.
Other results included an interesting observation in the static experiment: threshold contrast at the lowest adaptation luminance (0.07 cd/m2 (0.020 fL)) was lower than at higher adaptation luminances for all overhead lighting types and at all eccentricities. In the dynamic experiment at 0.07 cd/m2 (0.020 fL),the detection distance for all overhead-lighting types was also longer than that at 0.1 cd/m2 (0.03 fL), especially for 10- and 14-degree eccentricities. These findings could be attributed to the differential adaptation of the fovea compared with that at the periphery of the driver’s eye at the lowest adaptation luminance. However, more research is required to confirm these findings. Lastly, age was not a significant factor in either the static or dynamic portions of this experiment.