U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-15-065 Date: September 2015 |
Publication Number: FHWA-HRT-15-065 Date: September 2015 |
This section presents the SPFs developed for each State. The SPFs were used in the EB methodology to estimate the safety effectiveness of this strategy.(7) Generalized linear modeling was used to estimate model coefficients assuming a negative binomial error distribution, which is consistent with the state of research in developing these models. In specifying a negative binomial error structure, the overdispersion parameter, k, was estimated iteratively from the model and the data. For a given dataset, smaller values of k indicate relatively better models.
SPFs were calibrated separately for Minnesota, North Carolina, and Wisconsin using the corresponding reference sites from each State. The SPFs developed are presented by State in the following sections. Urban and rural segments were combined for modeling because of the limited sample sizes, particularly for some crash types. Factor variables were attempted for all models to account for any differences between urban and rural areas in terms of expected crashes.
Note that for sideswipe-opposite-direction crashes the number of crashes was very low, and these crashes were not analyzed.
The form of the SPFs for North Carolina freeways, which are presented in table 4, is shown in figure 7.
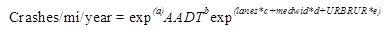
Figure 7. Equation. Form of SPFs for North Carolina.
Where:
AADT = Average annual daily traffic volume.
lanes = 1 if a four-lane road; 0 if greater than four lanes.
medwid = Median width in ft.
URBRUR = 1 if urban; 0 if rural.
a, b, c, d, e = Parameters estimated in the SPF calibration process.
k = Overdispersion parameter of the model.
Table 4. North Carolina freeway SPFs.
| Crash Type | Parameter Estimates (Standard Error) | |||||
| a | b | c | d | e | k | |
| Total | -11.5356 (1.4658) |
1.3273 (0.1286) |
-0.2662 (0.1664) |
-0.0130 (0.0039) |
— | 1.5431 |
| Injury | -12.6811 (1.3749) |
1.3152 (0.1201) |
-0.2428 (0.1571) |
-0.0094 (0.0036) |
— | 1.2591 |
| Run-off-road | -7.5439 (1.9691) |
0.6848 (0.1802) |
-0.5109 (0.1953) |
-0.0083 (0.0053) |
0.7401 (0.1926) |
1.6316 |
| Sideswipe-same-direction | -20.6539 (0.9716) |
1.9422 (0.0901) |
— | — | — | 0.9485 |
| Wet-road | -7.2571 (1.5024) |
0.8176 (0.1313) |
-0.6663 (0.1651) |
-0.0130 (0.0045) |
— | 1.5109 |
| Nighttime | -10.9313 (1.3845) |
1.1479 (0.1212) |
-0.2865 (0.1572) |
-0.0117 (0.0037) |
— | 1.2428 |
| Nighttime wet-road | -9.0525 (1.5366) |
0.8603 (0.1341) |
-0.5965 (0.1683) |
-0.0119 (0.0044) |
— | 1.1739 |
| — Indicates that the variable associated with parameter was not included in the SPF. | ||||||
In Wisconsin the data were directional, so the SPFs apply to one direction of travel only. The form of the SPFs for Wisconsin, which are presented in table 5 for freeways and table 6 for multilane roads, is shown in figure 8.
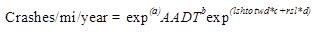
Figure 8. Equation. Form of SPFs for Wisconsin.
Where:
AADT = Average annual daily traffic volume.
lshtotwd = Total width left shoulder in feet.
rsl = 0 if rumble strip is present on left shoulder; 1 if not present (only applies for freeways).
a, b, c, d = Parameters estimated in the SPF calibration process.
k = Overdispersion parameter of the model.
Table 5. Wisconsin freeway SPFs.
| Crash Type | Parameter Estimates (Standard Error) | ||||
| a | b | c | d | k | |
| Total | -14.4921 (0.9000) |
1.6163 (0.0915) |
-0.1155 (0.0218) |
0.1729 (0.1369) |
0.5117 |
| Injury | -15.4639 (1.0433) |
1.6091 (0.1050) |
-0.1250 (0.0252) |
0.2276 (0.1521) |
0.4627 |
| Run-off-road | -6.5392 (1.0811) |
0.6094 (0.1097) |
-0.0548 (0.0265) |
0.2825 (0.1457) |
0.3635 |
| Sideswipe-same-direction | -20.4391 (1.2177) |
2.0075 (0.1159) |
-0.0943 (0.0258) |
— | 0.3287 |
| Wet-road | -17.3779 (1.2207) |
1.7533 (0.1182) |
-0.1301 (0.0294) |
— | 0.6121 |
| Nighttime | -14.6122 (1.1014) |
1.4966 (0.1100) |
-0.1220 (0.0251) |
0.4171 (0.1615) |
0.4998 |
| Nighttime wet-road | -18.2917 (1.9027) |
1.7034 (0.1786) |
-0.1354 (0.0411) |
— | 0.5154 |
| — Indicates that the variable associated with parameter was not included in the SPF. | |||||
Table 6. Wisconsin multilane divided SPFs.
| Crash Type | Parameter Estimates (standard error) | |||
| a | b | c | k | |
| Total | -11.1106 (1.6615) |
1.3452 (0.1723) |
-0.2588 (0.0326) |
0.5833 |
| Injury | -11.1247 (2.2012) |
1.2609 (0.2273) |
-0.2642 (0.0424) |
0.7870 |
| Run-off-road | -7.1200 (1.5806) |
0.5964 (0.1740) |
— | 0.2558 |
| Sideswipe-same-direction | -14.1156 (2.5936) |
1.4600 (0.2686) |
-0.2794 (0.0407) |
0.2880 |
| Wet-road | -15.6008 (3.1910) |
1.6419 (0.3310) |
-0.2483 (0.0528) |
1.0507 |
| Nighttime | -12.0965 (2.1780) |
1.2711 (0.2257) |
-0.1661 (0.0380) |
0.4843 |
| Nighttime wet-road | -19.8380 (4.2743) |
1.8316 (0.4600) |
— | 1.8614 |
| — Indicates that the variable associated with parameter was not included in the SPF. | ||||
The form of the SPFs for Minnesota, which are presented in table 7 and table 8, is shown in figure 9:
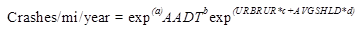
Figure 9. Equation. Form of SPFs for Minnesota.
Where:
AADT = Average annual daily traffic volume.
URBRUR = 1 if Urban area; 0 if Rural.
AVGSHLD = Average shoulder width in feet.
a, b, c, d = Parameters estimated in the SPF calibration process.
k = Overdispersion parameter of the model.
Table 7. Minnesota freeway SPFs.
| Crash Type | Parameter Estimates (Standard Error) | ||||
| a | b | C | d | k | |
| Total | -14.3723 (0.4805) |
1.5230 (0.0508) |
0.3279 (0.0975) |
-0.0396 (0.0138) |
0.5708 |
| Injury | -14.5068 (0.5238) |
1.4270 (0.0551) |
0.2286 (0.1045) |
-0.0408 (0.0141) |
0.5316 |
| Run-off-road | -10.0870 (0.3655) |
1.0144 (0.0367) |
— | -0.0427 (0.0142) |
0.5299 |
| Sideswipe-same-direction | -17.6510 (0.6394) |
1.6061 (0.0642) |
0.5061 (0.1239) |
— | 0.6457 |
| Wet-road | -16.8656 (0.6190) |
1.6012 (0.0643) |
0.4080 (0.1211) |
-0.0558 (0.0158) |
0.6772 |
| Nighttime | -15.4123 (0.5732) |
1.4999 (0.0599) |
0.1988 (0.1152) |
-0.0435 (0.0152) |
0.6361 |
| Nighttime wet-road | -18.7804 (0.8346) |
1.6686 (0.0852) |
0.4004 (0.1615) |
-0.0657 (0.0185) |
0.8175 |
| — Indicates that the variable associated with parameter was not included in the SPF. | |||||
Table 8. Minnesota two-lane undivided SPFs.
| Crash Type | Parameter Estimates (Standard Error) | ||||
| a | b | c | d | k | |
| Total | -8.3936 (0.1057) |
0.9379 (0.0158) |
0.5104 (0.0577) |
-0.0843 (0.0055) |
0.4390 |
| Injury | -8.1365 (0.1298) |
0.7822 (0.0197) |
0.3747 (0.0730) |
-0.0512 (0.0070) |
0.4106 |
| Run-off-road | -7.1823 (0.1337) |
0.6443 (0.0208) |
-0.2317 (0.0911) |
-0.0406 (0.0076) |
0.5454 |
| Sideswipe-same-direction | -14.9362 (0.4288) |
1.4366 (0.0584) |
0.6093 (0.1558) |
-0.1260 (0.0168) |
1.1590 |
| Wet-road | -11.1087 (0.2432) |
1.0215 (0.0353) |
0.7042 (0.1066) |
-0.0828 (0.0114) |
0.5333 |
| Nighttime | -8.4612 (0.1569) |
0.7791 (0.0237) |
0.4400 (0.0849) |
-0.0738 (0.0084) |
0.4770 |
| Nighttime wet-road | Use model for total with factor of 0.050 | ||||
| Head-on | Use model for total with factor of 0.040 | ||||
| Sideswipe-opposite-direction | Use model for total with factor of 0.034 | ||||
Because models for nighttime wet-road, head-on, and sideswipe-opposite-direction crashes could not be calibrated because of low numbers of crashes, predictions for those crash types used the model for total crashes with a multiplier for the proportion of total crashes that were of the respective crash type.