U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-086 Date: January 2018 |
Publication Number: FHWA-HRT-17-086 Date: January 2018 |
Table 39 provides the estimates of expected crashes in the after period without treatment, the observed crashes in the after period, and the estimated crash modification factor (CMF) and its standard error for each crash type considered in this study. The results in table 39 indicate reductions for all crash types analyzed in this study. The reductions are statistically significant at the 95-percent confidence level for all crash types. For all crash types combined, the CMFs are 0.917 for all severities and 0.899 for fatal and injury crashes. The crash type with the smallest CMF (which translates to the greatest reduction) is nighttime crashes with a CMF of 0.853 (or 14.7-percent reduction). The CMFs for rear-end and right-angle crashes are 0.933 and 0.941, respectively.
*Statistically significant results at the 95-percent confidence level.
The disaggregate analysis identified specific CMFs by crash type and different conditions. The process also revealed those conditions under which the multiple low-cost treatments are more effective. The research team identified several variables of interest, including: area type (urban or rural), number of legs (three or four), lane configuration of the mainline and the cross street, traffic volumes, and expected crashes without treatment. All of these variables are likely correlated, and caution should be exercised in interpreting and applying the disaggregate analysis results. The team did not conduct a disaggregate analysis on individual treatments or groups of treatments because no detailed information on type of treatment that each intersection received was available. Although we knew these intersections received at least some or all of the treatments, we did not know exactly what treatments were applied.
Table 40 presents the disaggregate results by area type (urban or rural), indicating the sample size (number of sites), CMF, and standard error of the CMF (in parentheses) by group for each crash type considered in this study. For the 188 urban intersections, the results in table 40 indicate increases in all crash types analyzed in this study. Specifically, the CMFs for total and fatal and injury crashes are 1.066 and 1.095, respectively, which are statistically significant at the 95-percent confidence level. The CMFs for rear-end, right-angle, and nighttime crashes are 1.006, 1.025, and 1.013, respectively, which are not statistically significant at the 95-percent confidence level. For the 245 rural intersections, the results in table 40 indicate reductions for all crash types analyzed in this study, which are all statistically significant at the 95-percent confidence level. Based on the disaggregate analysis by area type, it appears this strategy is highly effective at rural intersections, but there is the potential to increase crashes at urban intersections. However, as noted above, this effect may be due to other correlated variables.
*Statistically significant results at the 95-percent confidence level.
Table 41 presents the disaggregate results by number of legs, indicating the sample size (number of sites), CMF, and standard error of the CMF (in parentheses) by group for each crash type considered in this study. For the 242 three-legged intersections, the results in table 41 indicate reductions in all crash types analyzed in this study. The CMFs for total, fatal and injury, rear-end, and right-angle crashes are not statistically significant at the 95-percent confidence level. The CMF for nighttime crashes is 0.902 and is statistically significant at the 95-percent confidence level. For the 191 four-legged intersections, the results in table 41 indicate reductions for all crash types analyzed in this study, which are all statistically significant at the 95-percent confidence level. Based on the disaggregate analysis by number of legs, it appears this strategy is more effective at four-legged intersections than three-legged intersections. However, as noted above, this effect may be due to other correlated variables.
*Statistically significant results at the 95-percent confidence level.
Table 42 presents the disaggregate results by number of lanes, indicating the sample size (number of sites), CMF, and standard error of the CMF (in parentheses) by group for each crash type considered in this study. For the 257 intersections with two-lane major roads, the results in table 42 indicate reductions in all crash types analyzed in this study, which are all statistically significant at the 95-percent confidence level. For the 176 intersections with four-lane major roads, the results in table 42 indicate reductions in total, rear-end, right-angle, and nighttime crashes, and an increase in fatal and injury crashes. None of the CMFs associated with four-lane major roads are statistically significant at the 95-percent confidence level. Based on the disaggregate analysis by number of lanes, it appears this strategy is more effective at two-lane major road intersections than four-lane major road intersections. However, as noted above, this effect may be due to other correlated variables.
*Statistically significant results at the 95-percent confidence level.
Table 43 presents the disaggregate results by number of legs and number of lanes, indicating the sample size (number of sites), CMF, and standard error of the CMF (in parentheses) by group for each crash type considered in this study.
For the 126 three-legged intersections with two-lane major roads, the results in table 43 indicate reductions in all crash types analyzed in this study. The CMFs for total, fatal and injury, and nighttime crashes are 0.902, 0.811, and 0.828, respectively, which are statistically significant at the 95-percent confidence level. The CMFs for rear-end and right-angle crashes are not statistically significant at the 95-percent confidence level. For the 116 three-legged intersections with four-lane major roads, none of the CMFs are statistically significant at the 95-percent confidence level.
For the 131 four-legged intersections with two-lane major roads, the results in table 43 and table 44 indicate reductions in all crash types analyzed in this study. The CMFs for total, fatal and injury, right-angle, and nighttime crashes are 0.854, 0.816, 0.892, and 0.779, respectively, which are statistically significant at the 95-percent confidence level. The CMF for rear-end crashes is not statistically significant at the 95-percent confidence level, but is statistically significant at the 90-percent confidence level.
For the 60 four-legged intersections with four-lane major roads, the results in table 43 indicate reductions in all crash types analyzed in this study. The CMFs for total, rear-end, and nighttime crashes are 0.854, 0.838, and 0.780, respectively, which are statistically significant at the 95-percent confidence level. The CMFs for fatal and injury and right-angle crashes are not statistically significant at the 95-percent confidence level.
Based on the disaggregate analysis by number of legs and number of lanes, it appears this strategy is effective for most combinations of legs and lanes. It is least effective at three-legged intersections with four-lane major roads (i.e., 3 x 42). It is most effective at four-legged intersections with two-lane major roads (i.e., 4 x 22). However, as noted above, this may be due to other correlated variables.
*Statistically significant results at the 95-percent confidence level.
*Statistically significant results at the 95-percent confidence level.
Figure 29 and figure 30 show the individual CMFs for total crashes and fatal and injury crashes, respectively, for each treatment site compared to the total entering traffic volume associated with the intersection. The linear trend line suggests the multiple low-cost treatments are more effective on average for intersections with lower traffic volumes, and the effectiveness decreases (i.e., CMF increases) as traffic volume increases. The CMFs in both figure 29 and figure 30 appear to cross 1.0 when AADT is around 20,000. This suggests that the crash reduction potential is better for intersections with total entering AADT under 20,000. Again, the perceived relationship may also be due to correlations with other variables.
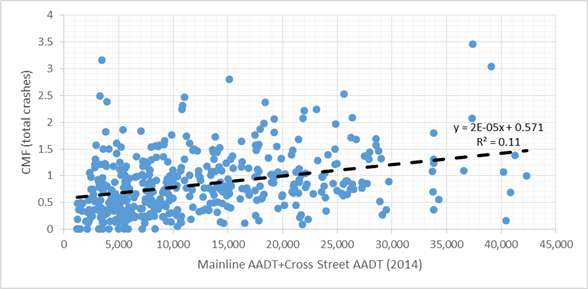
Source: FHWA.
Figure 29. Chart. Relationship between CMF (total crashes) and total intersection AADT.
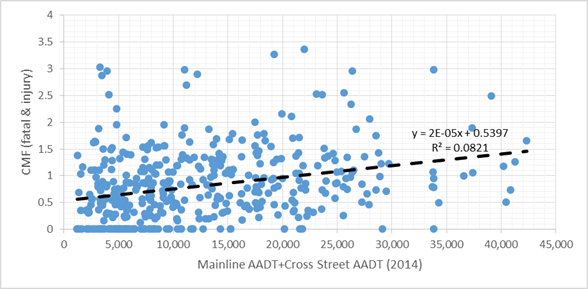
Source: FHWA.
Figure 30. Chart. Relationship between CMF (fatal and injury crashes) and total intersection AADT.
Figure 31 and figure 32 show the individual CMFs for total crashes and fatal and injury crashes, respectively, for each treatment site compared to the expected crashes per year in the before period. The linear trend line suggests the multiple low-cost treatments are more effective on average for intersections with fewer expected crashes per year in the before period, and the effectiveness decreases (i.e., CMF increases) as expected crashes increase. Note that this trend is consistent with the relationship for traffic volume as shown in figure 29 and figure 30, which makes sense because expected crashes increase as traffic volume increases. This confirms the need for caution when interpreting the results of the univariate analyses. Specifically, the net effect of the multiple correlations among variables investigated is a negligible effect on the expected number of crashes, which collectively captures the effects of those variables.