Prefabricated Steel Bridge Systems: Final Report
5. Optimization
A system optimization analysis is carried out to establish the maximum span lengths for the two modular systems presented in Chapter 4 and the most economical sectional design. The steel member design is optimized using global optimization methods. This chapter presents an overview of the different optimization methods and review the works reported in literature and related to steel member optimization.
5.1 Review of Global Optimization Methods
Let Ω be the space of design variables and let g(X) be the expected cost of the system being designed with XЄΩ. For large-scale optimization problems, the high-dimensional design space would generally contain numerous local minima scattered throughout the space. Common gradient-based or step-wise search methods tend to find local minima close to the starting position and are not suitable for large optimization problems. A desired optimization method should be able to perform a wider search for the global minimum, g*(X). While the global minimum may not be always identified, the method should go beyond the capabilities of a gradient-based or step-wise search.
In contrast to the traditional gradient-based optimization approaches, global optimization methods are usually stochastic. In recent years, metaheuristic search methods, based more on artificial reasoning than classical mathematics-based optimization approaches, have been successfully applied to handle some global optimization problems. Most of the stochastic global optimization methods belong to this category, such as simulated annealing [Kirkpatrick et al., 1983], tabu search [Glover and Laguna, 1993], and genetic algorithms [Goldberg, 1989]. There are other non-heuristic-based global optimization strategies such as multi-start optimization. The most popular global optimization methods are briefly reviewed in the following.
5.1.1 Review of methods and strategies
Simulated Annealing (SA): SA is a method simulating the physical process of metal annealing. It involves probabilistic transmissions among the solutions of the problem. Unlike local search algorithms which improve the objective function value at each iteration, some adverse changes are accepted in SA under the control of a randomized scheme. This compromise intends to bring the SA optimizer out of local optima traps and lead to a wider search for the global optimum. In the annealing process in which a metal at a high temperature is cooled down slowly and gradually, all the particles come from a high-energy level to a low-energy level stochastically. The eventual low-energy level depends on the level of the high temperature and the cooling rate. In this process, at each temperature T, the metal undergoes many random transmissions among different energy levels until a thermal equilibrium is satisfied according the Boltzmann distribution. When T is high, the probability of transmission to a higher energy level is large. As T decreases, the probability of accepting a transmission to a higher energy level also decreases.
SA simulates this process in the optimal search. Specifically, let a move from one solution Xk to another neighboring but inferior solution Xk+1 result in a change of the objective function value Δg. The probability of accepting this move is governed by:
(5.1)Pr(acceptance) = eΔg/T
Where T is a control parameter. Initially T is high, which allows many moves to inferior states, and it slowly reduces to a value where inferior moves are nearly always rejected. SA gives satisfactory solutions to many problems. However, it has a major disadvantage in the amount of computation involved.
Tabu Search (TS): TS is a history-based search. Like SA, it is based on neighboring searches with a local optima avoidance mechanism, but in a deterministic way which simulates the human memory processes. Here, memory is implemented by the implicit recording of previously seen solutions using simple but effective data structures. A tabu list is created to prohibit the search from going back to the moves which have been made in the recent past. This helps to avoid cycles in the search, and also promotes a diversified search in the search space. Let Xkbe the current move in the search. Most search strategies search the neighborhood of Xk, N(Xk), for the next move Xk+1; in TS, N (Xk) is replaced by N (H; Xk), where H is the history of the previous searches. This has the effect of prohibiting certain states of N (Xk). The simplest H is a record of the previously visited states. In enhanced versions, H may also include states that are not in N (Xk), which allows both diversification and intensification of the search. The two most important characteristics describing H are recency and frequency. Recency indicates the length of the history that is stored by H. Only the most recent moves were used as tabus, otherwise the search will be a straightjacket. Recency can be a fixed number or it can dynamically vary during the search. In contrast to the short-term memory that recency simulates, frequency simulates the long-term memory. There are two types of frequency measures: residence measure and transition measure. The former relates to the number to times a particular attribute is observed and the latter to the number of times an attribute changes from one value to another.
Genetic Algorithms (GA): GA has become the most well-known metaheuristic search method. GA is a probabilistic search method for solving optimization problems inspired by Darwin's theory of evolution and the natural law of survival of the fittest. Unlike SA and TS, GA uses a collection (population) of solutions for which a set of operations is executed that gradually improve the solution in succeeding populations. This method is used in this work and is therefore described in more details in section 5.3.2
Multi-start strategy: Combinations of metaheuristic-based searching methods are also used, e.g., combinations of GA with SA or SA with TS. A common drawback of metaheuristic-based searching methods is that they are not able to guarantee optimality either locally or globally. Therefore, these methods are usually combined with a multi-start strategy to perform gradient based or step-wise optimization to ensure that the final optimization result converges to at least a local optimum. Mathematically, a multi-start strategy is different from the above methods in that it is not metaheuristic-based. Typically, a multi-start strategy performs a local search from every point in an appropriate subset randomly drawn over, until certain stopping rules are met. The multi-start strategy provides a scheme of global optimization.
5.1.2 Review of Work Related to Steel Section Optimization
There has been interesting work in steel member optimization reported in the literature. [Seaburg and Salmon, 1971] investigated the optimization of hat-shaped steel members using gradient based search techniques; [Adeli and Karim, 1997] applied a neural dynamics model to optimize hat-, I- and Z-shapes; [Sarma and Adeli, 2000] further used this model to perform a comprehensive parametric study for hat-shape beams to look for the global optimum. Recently, [Lu, 2002] conducted a genetic algorithm (GA) optimization of Z- and Σ-shape purlins.
To advance the state-of-the-art of steel member optimization, two major issues must be addressed: the nonlinearities of the strength-based objective function and the inclusion of the set of all feasible cross-sections. The highly nonlinear nature of the strength of steel members is due to the fact that member strength is controlled by a complex combination of buckling modes and material strength. Common gradient-based optimization methods tend to be unreliable for such highly nonlinear objective functions.
In [Seaburg and Salmon, 1971], no convergence curve was given; in [Adeli and Karim, 1997] the method guarantees local optimum; in [Lu, 2002] the use of GA provides a general search, but no guarantee of convergence. Global searches [Seaburg and Salmon, 1971; Adeli and Karim, 1997; Karim and Adeli, 1999; Lu, 2002] have been possible only within a predefined scope of prototype shapes, which form a relatively small subset of all feasible cross sections.
5.2 Problem Formulation
This section provides the elements of the problem. The design parameters as well as the design objectives are first presented. This is followed by the assumptions considered and the design constraints related to the AASHTO LRFD Bridge Design Specifications [AASHTO 2003]. Finally, a flow chart illustrating an overview of the steel girder optimization process is provided.
5.2.1 Design Parameters
Fig. 5.1 shows a typical transverse bridge section made of a number of two-girder sections. The section which is considered for optimization is shown in Fig. 5.2. For such a two-girder section the fixed geometric parameters as well as the design variables are as follows:
- Fixed Values:
- Girder span l = 60 ft, 90 ft and 120 ft
- Girder distance s = 6 ft
- Slab thickness ts = 6 in and 8 in
- Concrete Strength fc = 5 ksi and 15 ksi
- Steel Yield Strength fy = 50 ksi
- Design Variables:
- Top flange width and thickness wt and tt
- Web height and thickness hw and tw
- Bottom flange width and thickness wb and t
Fig. 5.1 Typical bridge transverse section
Fig. 5.2 Section to be optimized
5.2.2 Design Objectives
The main objective of the optimization is to minimize the cost given the design constraints. For a girder with fixed length, this translates into the following objective function:
obj = w1 · t1 + hw · tw + w2 · t2
and the following optimization goal:
min{obj} subject to the design constraints
5.2.3 Assumptions
- The following assumptions are made in this study:
- The steel girder has a uniform cross section,
- The web and the flange are made from the same homogeneous material.
- Girders are used for simply supported spans only.
- Full Composite action.
- No longitudinal stiffeners are used. Transfer stiffeners are employed where necessary.
- The top plate receiving the concrete slab is not considered in the resisting system.
5.2.4 Design Constraints
The design constraints are related to the following aspects, as specified in LRFD codes:
- Dimension Limitations
- Section Proportion Limits
- Flexural Strength Capacity
- Shear Strength Capacity
- Fatigue and Fracture
- Service Limit State
- Constructability Check
Specifically, this translates into the following constraints:
Minimum Steel Dimensions
To guard against local buckling minimum steel dimensions need to be defined. In the optimization analysis the minimum steel dimensions defined in the Florida Department of Transportation (FDOT) design guidelines are used.
Source: http://www.dot.state.fl.us/structures/StructuresManual/CurrentRelease/FDOTBridgeManual.htm
These minimum dimensions are as follows:
tw = 7 + n · 1 inch n = 0,1,2,...,33 16 16 The minimum web thickness is 7/16 inch and the increments is 1/16 inch when the thickness is no greater than 2 1/2 inch.
tw = 1 + n · 1 inch n = 0,1,2,... 2 4 The increment is 1/8 inch when the web thickness is greater than 2 1/2 inch.
tt,tb = 3 + n · 1 inch n = 0,1,2,...,14 4 8 The minimum flange thickness for plate girders and top flanges of box girders is 3/4 inch and the increments is 1/8 inch when the plate thickness is no greater than 2 1/2 inch.
tt,tb = 2 1 + n · 1 inch n = 0,1,2,... 2 4 The increment is 1/4 inch when the plate thickness is greater than 2 1/2 inch.
wt,wb ≥ 12 inch
The minimum flange width for plate girders and top flanges of box girders is 12 inch.
Non-Composite Section Property Constraints
Based upon flexural considerations, I-section proportions shall satisfy the following inequalities:
(LRFD 6.10.2.1-1)0.1 ≤ Iyc ≤ 0.9 Iy Where I yc : moment of inertia of the compression flange, and I y : moment of inertia of the non-composite flange.
Webs shall be proportioned such that:
(LRFD 6.10.2.2-1)2 Dc ≤ 6.77 E ≤ 200 tw fc Where Dc : depth of the web in compression in the elastic range.
Compression flanges shall be proportioned such that:
(LRFD 6.10.2.3-1)wt ≥ 0.3 Dc
If the section is non-compact, the compression flange slenderness has to be subjected to the following extra constraint:
(LRFD 6.10.4.1.4-1)wt ≤ 12.0 2 tt Tension flanges shall be proportioned such that:
(LRFD 6.10.2.3-2)wb ≤ 12.0 2 tb Flexural Strength Constraints
- Composite section property calculation
Effective flange width for concrete slab (LRFD 4.6.2.6)
- interior beam: b = min { 1/4 l , 12 ts + max { tw , 0.5wt } , s }
- exterior beam: b = 0.5 binterior + min { 1/8 l, 6 ts + max { 0.5 tw, 0.25 wt } , boverhang }
Transformed concrete slab area
A′ = A or A For long and short-term loads, respectively 3n n Concrete modular ratio
n = 10 if 2.4 ≤ f′c ≤ 2.9 n = 9 if 2.9 ≤ f′c ≤ 3.6 n = 8 if 3.6 ≤ f′c ≤ 4.6 n = 7 if 4.6 ≤ f′c ≤ 6.0 n = 6 if 6.0 ≤ f′c - Flexural strength calculation
Pb = wb · tb · fy Pt = wt · tt · fy Pw = ww · tw · fy Ps = A′ · f′c - If Pb + Pw ≥ Pt + Ps (neutral axis is in web)
y = hw · Pb - Pt - Ps + 1 2 Pw Mp = Pw · [ y2 + ( hw - y )2 ] + [ Psds + Ptdt + Pbdb ] 2 hw - If Pb + Pt + Pw ≥ Ps (neutral axis is in top flange)
y = tt · Pw - Pb - Ps + 1 2 Pt Mp = Pt · [ y2 + ( tt - y )2 ] + [ Psds + Pwdw + Pbdb ] 2 tt - Else (neutral axis is in slab)
y = ts · Pw + Pb + Pt Ps Mp = y2 Ps + [ Ptdt + Pwdw + Pbdb ] 2 ts
The depths of the web in compression in the elastic and plastic ranges are respectively:
Dc = fDC1 + fDC2 + fDW + fLLM - tt fDC1 + fDC2 + fDW + fLLM csteel c3n cn and
Dcp = hw fy tb wb - fy tt wt - 0.85 f′c A + 1 if neutral axis is in the web 2 fy tw hw 0 otherwise The calculation of girder flexural strength depends on whether the girder section is compact or non-compact.
- Compact section:
A section is considered compact if the following 2 conditions are satisfied:
- Condition 1:
fy ≤ 70 ksi
- Condition 2:
2 Dcp ≤ ( 0.75 ) 3.76 E and 2t ≤ ( 0.75 ) 0.382 E tw fyc 2 tt fyc OR
2 Dcp ≤ 3.76 E and wt ≤ 0.382 E and 2 Dcp + 9.35 wt ≤ 6.25 E tw fyc 2 tt fyc tw 2 tt fyc
The calculation of nominal flexural strength Mn for compact sections is shown below
(LRFD 6.10.4.2.2b)D′ = β d + ts + th 7.5 Where
b = 0.9 for fy = 36 ksi = 0.7 for fy = 50 ksi = 0.7 for fy = 70 ksi d = depth of the steel section th = thickness of the concrete haunch above the top flange ts = thickness of the concrete slab - If Dp ≤ D′, then
(LRFD 6.10.4.2.2a-1)
Mn = Mp
- If D′ < Dp ≤ 5 D′, then
(LRFD 6.10.4.2.2a-1)
Mn = 5 Mp - 0.85 My + 0.85 My - Mp Dp 4 4 D′ Where My = Moment capacity at first yield of the short-term composite positive moment section.
- Otherwise, the nominal flexural resistance is calculated using the equation below but not greater than the value of Mn calculated from the above two equations.
(LRFD 6.10.4.2.2a-3)
Mn = 1.3 Rh My
Where Rh = hybrid factor specified in LRFD 6.10.4.3.1
- Condition 1:
- Non-compact section:
The stresses in tension and compression flanges of non-compact sections are calculated as:
- Tension flange
(LRFD 6.10.4.2.4a-1)
fn = Rb Rh fyt
Where
Rh = 1 - βψ ( 1 - ρ )2 ( 3 - ψ + ρψ ) 6 + βψ ( 1 - ψ ) ρ = fyw / fyb β = Aw / Afb ψ = db / d (db is calculated based on short-term composite section) Rb = 1 if 2 Dc ≤ λb E tw fc 1 - ar 2 Dc - λb E otherwise 1200 + 300 ar tw fc ar = 2 Dc tw Ac λb = 5.76 if Dc ≤ hw 2 4.64 otherwise - Compression flange
fn = Rb Rh fyc
- Tension flange
(LRFD 6.10.4.2.4a-1)
- If Pb + Pw ≥ Pt + Ps (neutral axis is in web)
- Flexural strength constraints
The flexural strength constraints can be therefore formulated as
φf Mn ≥ Mu For compact sections, and φf fn ≥ fu For non-compact sections
- Composite section property calculation
Shear Strength Constraint
(LRFD 6.10.7.3.2-2)If hw > 150, transverse stiffeners shall be used with the spacing satisfying tw d0 ≤ hw 260 2 ( hw / tw ) The maximum shear force is in the end panel. If the girder has a uniform section, the shear design check needs to be performed only for the end panel.
(LRFD 6.10.7.3.3c-1)Vn = CVp
Where Vp = plastic shear force; and C = ratio of the shear buckling stress to the shear yield strength specified, as given below:
Vp = 0.58 fcw hw tw
C = 1.0 if hw < 1.10 Ek tw fyw 1.10 if 1.10 Ek ≤ D ≤ 1.38 Ek hw / tw fyw tw fyw 1.52 if D > 1.38 Ek ( hw / tw )2 tw fyw The shear strength constraint is defined as:
φv Vn ≥ Vu
Service Limit Constraints
For both steel flanges of composite sections:
(LRFD 6.10.5.2-1)ff ≤ 0.95 fy
Where ff = elastic flange stress caused by the factored loading.
The web must satisfy the following requirement:
(LRFD 6.10.3.2.2-1)fcw ≤ 0.9 Eαk ≤ fyw hw 2 tw Where
fcw = maximum compression stress in the web α = 1.25 k = 9.0 ( hw / Dc )2 Web Fatigue Strength Constraint
The live load flexural stress and shear stress resulting from the fatigue load shall be taken as twice the value calculated using the fatigue load combination in LRFD, Table 3.4.1-1
- Flexure
Webs without longitudinal stiffeners shall satisfy the following constraint
(LRFD 6.10.6.3)If 2 Dc ≤ 5.7 E tw fyw fcf ≤ fyw
Else
fcf ≤ 32.5 E tw 2 2 Dc Where
fcf = maximum compressive elastic flexural stress in the compression flange due to the un-factored permanent load and the fatigue loading fcw = specified minimum yield strength of the web - Shear
Webs of homogeneous sections with transverse stiffeners must satisfy
(LRFD 6.10.6.4)Vcf ≤ 0.58 Cfyw
Where Vcf = maximum elastic shear stress in the web due to the un-factored permanent load and the fatigue loading
- Flexure
Flange Fatigue Resistance Constraint
Nominal fatigue resistance shall satisfy:
( Δf )n = A 1/3 ≥ 1 ( Δf )th N 2 Where
N = ( 365 ) ( 75 ) n ( ADTT )SL A = constant taken from LRFD Table 6.6.1.2.5-1 n = number of stress range cycles per truck passage from LRFD Table 6.6.1.2.5-2 ( ADTT )SL = single-lane ADTT specified in LRFD 3.6.1.4 ( Δf )th = constant-amplitude fatigue threshold from LRFD Table 6.6.1.2.5-3
5.2.5 Optimization Flow Chart
The flow chart presented in Fig. 5.3 illustrates the process of the steel girder optimization. As can be seen from this flow chart, the optimization process starts with an initial design. The latter is evaluated using the function evaluation drive, i.e., the objective functions and the constraints functions. It then proceeds through an optimization engine, which generates new design. The latter is then sent for evaluation to the function evaluation drive. This process is continued until either the iteration converges or the maximum number of iterations is reached.
Fig. 5.3 Optimization Flow Chart
5.3 Optimization Strategies and Methodology Used
5.3.1 Overview
Global optimization (GO) is a multi-start optimization strategy. For every multi-start optimization strategy, two problems have to be addressed: how to select the starting points to begin the consequent local searches and when to stop the local searches. In GO, the GA is used to select promising starting points. Mathematically the GO is described by Equations 5.2 and 5.3 given below. These equations express the meaning of multi-start optimization. In Equation 5.2, it is assumed that convergence of the gradient-based or step-wise optimization is guaranteed. Based on this assumption, a sampling scheme is proposed to further increase the local optimization seed quality, as well as improve the chance of discovering better designs during the global optimization process.
5.2
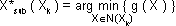
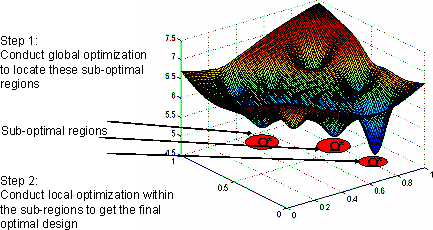
The sampling scheme and the local optimization seed selection are performed via GA in this study. The local optimization method we choose herein is SBO. GA and SBO are described in sections 5.3.2 and 5.3.3, respectively. The optimization strategy used in this work is illustrated in Fig. 5.4, where the GA is used to locate the sub-optimal regions Ω*, while SBO is used to optimize each sub-region.
Fig. 5.4 Optimization Strategy
5.3.2 Genetic Algorithms (GA)
Genetic algorithms are a class of optimization strategies that simulate the mechanisms of genetic evolution, first proposed and analyzed by [Holland, 1975]. GA is well-known for its global optimization ability and easy format for constraint statements. With these advantages, it has been applied widely in complex structural optimization problems [Sarma and Adeli, 2000; Camp et al., 1998; Jenkins, 1992; Pazeshk et al., 2000; Rajeev and Krishnamoorthy, 1997; Lagaros et al., 2002]. GA intends to explore the natural relationship among the better designs and use this relationship to guide the optimal search, however, in an implicit manner.
There are many variations of GA. However, in this study the canonical GA [Holland, 1975; Goldberg, 1987] is used. For a review of different GA methods, readers are referred to [Back et al., 2000a, b].
In canonical GA, a design variable vector is represented by a string of binary numbers, named a chromosome, or a gene string. Differing from tradition optimization methods that deal with only one design at a step during the iteration, a GA operates on a population of gene strings, which is called a generation. According to the objective function value and satisfaction of constraints, a measurement, fitness, is assigned to each design. Consequently, an algorithm selects some gene strings as parents from the current population to generate the next generation. As this procedure repeats, the generations evolve and it is expected that after enough iterations, optimal designs will be reached.
A canonical GA consists of three parts: (a) gene coding and decoding scheme, which is a one-to-one mapping between design variables and gene strings; (b) fitness definition; and (c) genetic operators for creating the next generation. Commonly used genetic operators include selection, crossover and mutation. Usually these genetic operators are stochastic and thus GAs belong to the category of stochastic optimization algorithms.
Selection operators select pairs of parent strings from the chromosome pool of a generation. Typically, each string is assigned a probability of being selected. In the next step of GA, variation of genes are introduced by crossover and mutation based on the selected pairs of parent strings.
Crossover is a procedure that randomly breaks the selected parent strings into segments and swaps some segments of a parent string with another parent string. According to the number of segments a parent string is broken into, there are: 1-point crossover, 2-point crossover and so on. By introducing new strings, crossover creates variations in the next generation, but the parts of the new strings are taken from the previous generation, which exhibits an inheritance property.
Mutation changes some gene codes stochastically, which brings in nonexistent feature into the population. This procedure may be thought of as an insurance policy against local minima as it insures that part of the generation is scattered throughout the design space. Mutation enables GA search all the regions in the work space if the GA running time is infinite. It directs GA to some search directions that could have never been looked into without the mutation procedure.
5.3.3 Surrogate Based Optimization (SBO)
A surrogate function is a low-definition function approximating the high-definition function. A surrogate-based optimization approach is designed to manage surrogate models of the objective function and constraints during the optimization process. In the sequence of optimization steps, surrogate models are kept updated by the exact objective function and constraints, while the surrogates are moving towards the local optimum. Thus, surrogate-based optimization is also called sequential approximation optimization (SAO) [Conn et al., 1993, 1994; Rodriguez et al., 1997, 1998].
There are two major advantages of using SBO. Firstly, the evaluation of surrogate functions is faster than the original objective function. To fully simulate this objective function in high-dimensional design space requires too many objective function evaluations. Constructing a surrogate model requires considerably less objective function evaluations and hence speeds up optimization. Secondly, and perhaps more importantly, the objective function is neither smooth nor continuous. For numerical objective functions, the inherent numerical noise, such as that arising from poorly resolved computational meshes; add more non-smooth trends to the functions that reduce the efficiency and probability of convergence of gradient-based optimization methods. Surrogate models smooth out the noise, so that gradient-based optimization methods can be used.
Similar to multi-start optimization, SBO also decomposes an optimization problem into a sequence of sub-problems, albeit at a more local scale. In every step of the optimization sequence, a surrogate function is limited to a small region, fitting a limited number of points of objective function values. An SBO process has two principal components, surrogate model construction and management strategy. Considering the constraints of this local optimization problem, an augmented Lagrangian method [Liu 2003] is used herein.
Surrogate functions (response surfaces) were first developed for fitting models of physical experiments and later were adapted into the structural optimization process. In the construction of a surrogate, the type of the approximation function is pre-selected. With a sufficient number of design points evaluated in a sub-region, a relatively simple function is used to approximate the exact function. There are a lot of surrogate methods, including polynomial regression [Myers, 1995], artificial neural networks [Zimmerman, 1996], multivariate regression splines [Friedman, 1990], kriging interpolation [Giunta and Watson, 1998] and classifier systems [Lee and Hajela, 2001]. Among them, polynomial regression has the simplest form and is used in this study.
A convergence criteria informs the SBO algorithm when to stop the iteration process [Liu 2003].
In SBO, a sequence of surrogate models are generated which gradually approaches the optimum design point. A management strategy is required to guide the search direction, as well as adjust the size of the sub-region so that the surrogate model fits this region well [Liu 2003].
5.4 References
- AASHTO. 2003. AASHTO LRFD Bridge Specifications, American Association of State Highway and Transportation Officials. Second Edition.
- Adeli, H. and Karim, A. 1997. Neural network model for optimization of cold-formed steel beams.Journal of Structural Engineering, ASCE, 123(11):1535 -1543.
- Back, T., Fogel, D. B. and Michalewicz, T. Editors. 2000a. Evolutionary Computation 1: Basic Algorithms and Operators. Institute of Physics Publishing.
- Back, T., Fogel, D. B. and Michalewicz, T. Editors. 2000b. Evolutionary Computation 2: Advanced Algorithms and Operators. Institute of Physics Publishing.
- Camp, C., Pezeshk, S. and Cao, G. 1998. Optimized design of two-dimensional structures using a genetic algorithm. Journal of Structural Engineering, ASCE, 124(5):551 -559.
- Conn, A. R., Gould, N. I. M., Sartenaer, A. and Toint, P. L. 1993. Global convergence of a class of trust region algorithms for optimization using inexact projections on convex constraints. SIAM Journal on Optimization, 3:164 -221.
- Friedman, J. H. 1990. Multivariate adaptive regression splines. Technical report, Stanford Linear Accelerator Center.
- Giunta, A. A. and Watson, L. T. 1998. A comparison of approximation modeling techniques: polynomial versus interpolating models. In Proceedings of the 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Design, pages 392 -404.
- Glover, F. and Laguna, M. 1993. Tabu search. In C. Reeves, Editor, Modern Heuristic Techniques for Combinatorial Problems, Oxford, England, Blackwell Scientific Publishing.
- Goldberg, D. E. 1987. Simple genetic algorithm and the minimal deceptive problem. In Research Notes in Artificial Intelligence, chapter 6, pages 74 -88. Morgan Kauffmann Publishers Inc.
- Goldberg, D. E. 1989. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley.
- Holland, J. H. 1975. Adaptation in Natural and Artificial Systems. University of Michigan Press.
- Jenkins, W. M. 1992. Plane frame optimum design environment based on genetic algorithm. Journal of Structural Engineering, ASCE, 118(11):3103 -3112.
- Karim, A. and Adeli, H. 1999. Global optimum design of cold-formed steel hat-shape beams. Thin-Walled Structures, 35(275 -288).
- Kirkpatrick, S. Gelatt, C. D. and Vecchi, M. P. 1983. Optimization by simulated annealing. Science, 220(4598):671 -680.
- Lagaros, N. D., Papadrakakis, M. and Kokossalakis, G. 2002. Structural optimization using evolutionary algorithms. Computers and Structures, 80:571 -589.
- Lee, J. and Hajela, P. 2001. Application of classifier systems in improving response surface based approximation for design optimization. Computers and Structures, 79:333 -344.
- Liu, H. 2003. Bayesia classifiers for uncertainty modeling with applications to global optimization and solid mechanics problems. Ph.D. Thesis, The Johns Hopkins University, Baltimore, Maryland, USA.
- Lu, W. 2002. Optimum design of cold-formed steel purlins using genetic algorithms. PhD Thesis, Helsinki University of Technology.
- Myers, R. H. 1995. Response Surface Methodology: Process and Product Optimization Using Designed Experiments. John Wiley & Sons, Inc., New York, NY.
- Pazeshk, S. Camp C. V., and Chen, D. 2000. Design of nonlinear framed structures using genetic optimization. Journal of Structural Engineering, ASCE, 126(3):382 -388.
- Rajeev, S. and Krishnamoorthy, C. S. 1997. Discrete optimization of structures using genetic algorithms-based methodologies for design optimization of trusses. Journal of Structural Engineering, ASCE, 123(3):350 -358.
- Rodriguez, J. F., Renaud, J. E., and Watson, L. T. 1997. Trust region augmented Lagrangian methods for sequential response surface approximation and optimization. In Proceedings of the ASME design engineering technical conference.
- Rodriguez, J. F., Renaud, J. E., and Watson, L. T. 1998. Convergence of trust region augmented Lagrangian methods using variable fidelity approximation data. Structural Optimization.
- Sarma, K. C. and Adeli, H. 2000. Fuzzy genetic algorithm for optimization of steel structures. Journal of Structural Engineering, ASCE, 126(5):596 -604.
- Seaburg, P. A. and Salmon, C. G. 1971. Minimum weight design of light gage steel members. J. Struct. Div., ASCE, 97(1):203 -222.
- Zimmerman, D. 1996. Genetic algorithms for navigating expensive and complex design spaces. Technical report, Sandia National Laboratories.

