AHP Comparison Framework
"What is the worth of a specific bridge construction technique in terms of a customer service criterion?"
Although information about questions like the previous one are vital in making the correct decision, it is very difficult, if not impossible, to quantify them correctly. Therefore, many decision-making methods attempt to determine the relative importance, or weight, of the alternatives for each criterion involved in a given decision-making problem.
Pairwise comparisons are used to determine the relative importance of each alternative for each criterion. In this approach the decision-maker has to express his opinion about the value of one single pairwise comparison at a time.
Each choice is a linguistic phrase. Some examples of such linguistic phrases are: "A is more important than B", or "A is of the same importance as B", or "A is a little more important than B", and so on.
For instance, when system A is compared to system B then the decision-maker has determined that system A is between to be classified as "essentially more important" and "demonstrated more important" than system B (see also Table1 and Table2). Thus, the corresponding comparison assumes the value of 6.
Table1 and Table2 are both representing the AHP comparison scales. The difference between these tables are in the way that scales are qualified (represented by words). Decision makers can consider both tables in the pairwise comparison process, to choose and assign the scores more rigorously.
| Intensity of Importance | Definition | Explanation |
|---|---|---|
| 1 | Equal importance | Two activities contribute equally to the objective |
| 3 | Weak importance of one over another | Experience and judgment slightly favor one activity over another |
| 5 | Essential or strong importance | Experience and judgment strongly favor one activity over another |
| 7 | Demonstrated importance | An activity is strongly favored and its dominance demonstrated in practice |
| 9 | Absolute importance | The evidence favoring one activity over another is of the highest possible order of affirmation |
| 2,4,6,8 | Intermediate values between the two adjacent judgments | When compromise is needed |
| Reciprocals of above nonzero | If activity i has one of the above nonzero numbers assigned to it when compared with activity j, then j has the reciprocal value when compared with i. |
| The Fundamental Scale for Pairwise Comparisons | ||
|---|---|---|
| Intensity of Importance | Definition | Explanation |
| 1 | Equal Immportance | Two elements contribute qually to the objective |
| 1 | Moderate importance | Experience and judgement slightly favor one element over another |
| 5 | Strong importance | Experience and judgement strongly favor one element over another |
| 7 | Very strong importance | One element is favored very strongly over another; its dominance is demostrated in practice |
| 9 | Extreme importance | The evidence favoring one element iver another is of the highest possible order of affirmation |
| Inensive of 2, 4,6, and 8 can be used to express intermediate values. Intensities 1.1, 1.2, 1.3, etc. can be used for elements that are very close in importance | ||
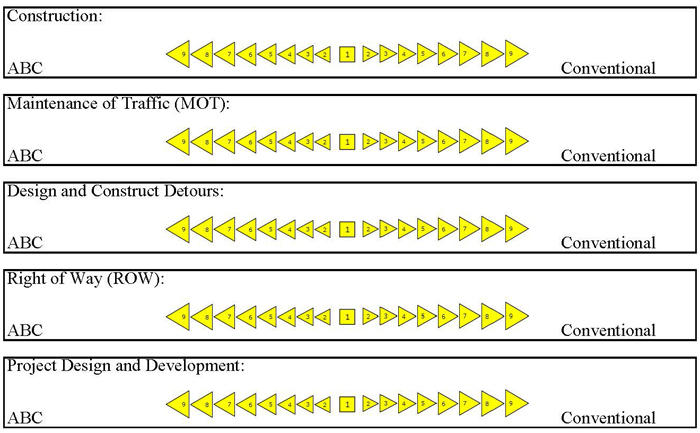
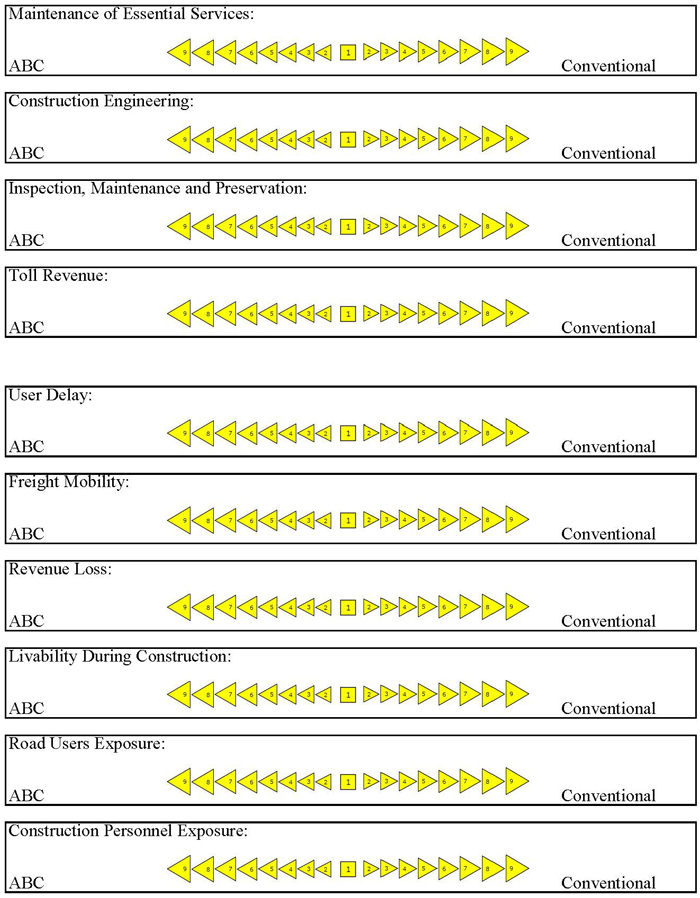
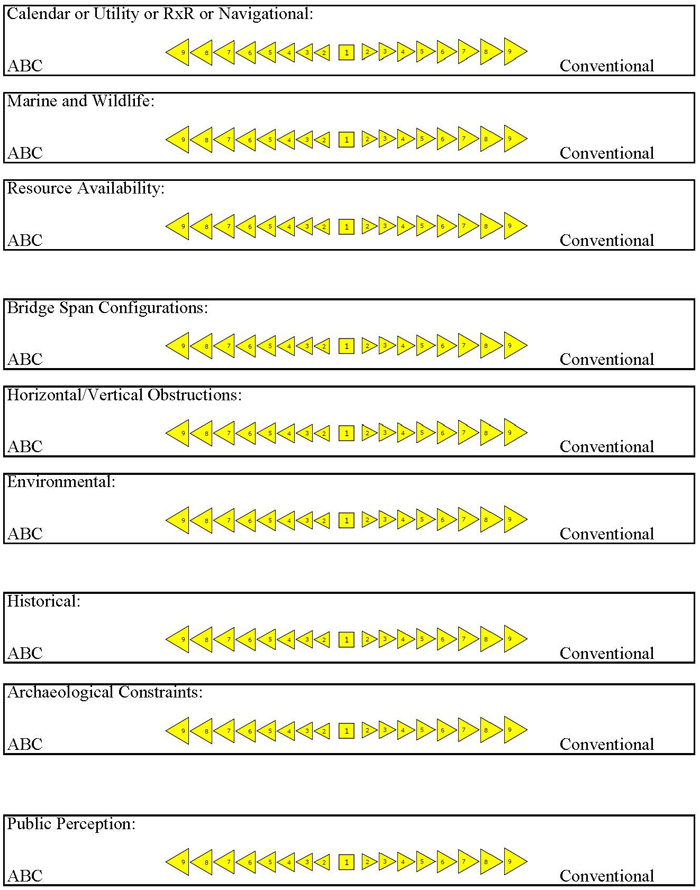
Please indicate the level of preference by choosing the most descriptive score (both value and direction) in the rubrics below.
Level 1
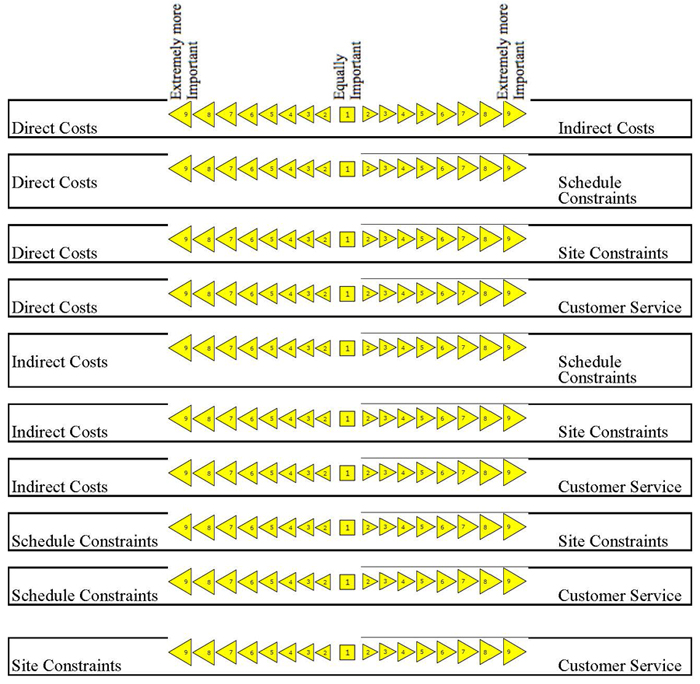
Level 2

Level 3