U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-094 Date: February 2015 |
Publication Number: FHWA-HRT-14-094 Date: February 2015 |
Pullout and rupture of reinforcement are two modes of failure that have been identified for checking the internal stability (stability within reinforced zone) in the design of a reinforced soil wall or abutment. The pullout check is performed to determine required reinforcement length, whereas the rupture check is conducted to determine required reinforcement strength. The need to check pullout failure stems from the fundamental design concept of GMSE systems in which the reinforcement is considered as tiebacks acting as tension members to "hold" an assumed failure wedge in place (see figure 1), thus preventing it from sliding down and away from the rest of the reinforced soil mass.
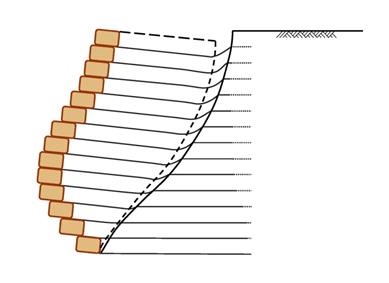
Figure 1. Drawing. Pullout failure, exaggerated for purposes of illustration.
In the three major design guidelines for reinforced soil walls and abutments-AASHTO Standard Specifications for Highway Bridges, FHWA NHI manual, and NCMA design manual-the check of reinforcement pullout is performed by requiring the reinforcement be long enough that the "resisting force" (resulting from soil-reinforcement interface friction/interlocking resistance) beyond an assumed slip plane be sufficiently greater than the "driving force" (earth thrust within the tributary zone) for "any" level of a reinforcement layer.(1,2,3) A minimum safety factor of 1.5 and a minimum anchored length of 2.95 ft (0.9 m) have typically been specified to assure pullout failure will not occur.
The driving force at a given reinforcement layer is evaluated by multiplying the reinforcement spacing by the lateral stress in the tributary zone along an assumed critical slip plane. On the other hand, the resisting force of a geosynthetic reinforcement layer is determined by multiplying the unit interface shear resistance by the length of reinforcement behind the assumed slip plane. Both forces require a realistic assumption of the location of the most critical slip plane, which may be a function of, among other factors, soil friction angle and facing rigidity.
To develop a sound design concept, checking reinforcement pullout of a GMSE system is needed. This is because if a tieback system does not have a sufficient anchor length, the system is destined to fail. However, for a GRS system, the same is not true. Reinforcement length in a GRS system is determined by external stability. In a GRS system, geosynthetic reinforcement is considered to be tensile inclusion, which serves to improve soil stiffness and strength (through such reinforcing mechanisms as inducing apparent cohesion, increasing confinement, suppressing dilation, and reducing lateral deformation). Because geosynthetic reinforcement layers are not considered tieback members, the necessity to check geosynthetic pullout for a GRS system has become a debatable issue.
Those who insist that geosynthetic pullout failure should not be checked for a GRS system have stated that if the design protocol of a GRS system involves checking pullout failure, the design has resorted to the tieback concept, which violates the fundamental design concept of GRS systems-it is like "mixing apples and oranges." In addition, the pullout check is confusing and redundant for GRS systems.
On the other hand, those who maintain that geosynthetic pullout should be checked have argued that checking geosynthetic pullout failure is a simple step in a design, and therefore, it would not be a drawback to perform that extra step to ensure pullout stability. Although this argument sounds reasonable, it is perhaps not so simple.
A great deal of research effort has been expended on the determination of reinforcement length to ensure stability against pullout failure. Since the 1980s, hundreds of studies have been conducted on the subject of a simple test called the "pullout test." Huang collected 478 sets of pullout tests for a statistical analysis.(31) In a pullout test, a reinforcement element (metallic strip, metallic mesh, geosynthetic strip, geosynthetic sheet, etc.) is confined in soil under a constant surcharge, inside a test bin, and is subject to increasing tensile loads. Pullout tests that have been performed range from small- to large- to field-scale tests, from short- to long-term tests, Â from static to cyclic tests, from laboratory to field tests, from drained to undrained tests, from unsaturated to saturated tests, from finite element/difference analysis to close-form solution, and include centrifuge model tests.(See references 32 through 37.)
It is to be noted that pullout tests in fact only address the interface shear resistance that occurred beyond an assumed slip surface. In a pullout test, the location of the failure surface is not of concern; i.e., it does not address the question of the available resisting force in its entirety. For a GRS wall, it has been tacitly assumed that the Rankine or Coulomb active failure surface for a "uniform" soil mass is applicable to a reinforced soil mass that contains layers of geosynthetic reinforcement (e.g., AASHTO, Berg et al., and NCMA).(1,2,3)
After an exhaustive search of the literature, a single case of "in-service" reinforced soil wall, including both GMSE walls and GRS walls, was not found in which failure can be clearly attributed to pullout of reinforcement. Part of the reason pullout failure is difficult to identify is because, unless a distinct failure surface is fully developed, pullout of reinforcement is "buried" and not visible without careful reconnaissance work that involves removing the covering soil. It is conceivable that pullout failure in a reinforced soil wall or abutment may occur under certain combinations of the following conditions: (a) reinforcement is very stiff and has very high strength; (b) backfill is loosely compacted, or cohesive and wet; (c) reinforcement spacing is large (say, greater than 1.97 ft (0.6 m)); and (d) reinforcement is relatively long (say, ≥ 0.6H).
Suah and Goodings performed 27 centrifuge model tests of wrapped-faced geotextile walls, all with 100-percent clay backfill.(38) The reinforcement lengths varied from 0.5 to 1.5H. All the tests were brought to failure. Wall failure in all the tests occurred by tensile breakage of the geotextile, and never by pullout. This is contrary to the popular perception that clayey backfill is highly susceptible to pullout failure, and often cited as the primary disadvantage of employing clayey backfill in construction of a reinforced soil wall. Suah and Goodings also indicated that when reinforcement was short (0.5H), prefailure differential settlement at the front of the wall was pronounced, and failure by overturning was likely; when reinforcement was longer (1.0 to 1.5H), differential settlement was less pronounced, and sliding along an inclined failure surface was more likely.
Woodruff performed a series of centrifuge model tests to examine potential failure surfaces of shored GMSE walls.(27) Yang et al. investigated the same subject using a limit equilibrium approach.(39) The two studies came to a similar conclusion that the critical failure plane for reinforcement length less than 0.7H was bilinear. The inclination angle of the critical failure plane within a shored GMSE wall is 10- to 20-percent less than that of the Rankine theory and extends along the contact surface between the back of the reinforced wall and the shored wall.
It is interesting to note that Leshchinsky and Vulova conducted a parametric study, using a finite difference program, Fast Lagrangian Analysis of Continua, or FLAC, to examine the effects of various parameters on GMSE walls with segmental facing.(40) Factors such as backfill strength, foundation strength, reinforcement stiffness, soil-reinforcement interface strength, reinforcement spacing, and wall height were examined. The study indicates that for closely spaced reinforcement (spacing less than 1.31 ft (0.4 m) in their definition), the critical slip plane did not pass through the reinforced soil zone. They suggest that a method different from Rankine or Coulomb analysis is needed to assess internal stability of a closely spaced GMSE wall. They also argue that the reason many experiments were able to bring about internal failure was because those walls do not typically represent realistic prototypes. They offered the following analogous example:
Consider the case of a rigid, non-yielding (unreinforced) retaining wall. Correct design would use at-rest lateral earth pressures reflecting the impossibility of an active wedge developing within the retained soil (a unrealistic failure mechanism). However, one can conduct an experiment on such a structure and impose the active case by exerting very large surcharges (i.e., cause yielding of the wall). Such an unrealistic experiment may lead to the incorrect conclusion that, for non-yielding walls, active soil pressures should be used. That is, the observed failure mechanism in the experiment is not necessarily relevant to the prototype. (page 363)(40)
As noted in earlier in this synopsis, evaluation of pullout failure involves calculations of driving forces and resisting forces, and both involve the knowledge of the location of the critical slip plane (often taken as the plane of maximum reinforcement loads). The following presents studies on the location of the critical slip plane and on the lateral thrust for the determination of the driving forces.
Critical Slip Plane
Tatsuoka pointed out that facing rigidity has a significant effect on the distribution of tensile forces induced in the reinforcement (see figure 2).(41) For reinforcement securely connected to rigid facing, the largest tensile force occurs near the wall face; whereas it occurs away from the wall face if the connection force is small. The distribution of reinforcement loads, hence the location of the critical slip plane, is strongly affected by the rigidity of the facing.
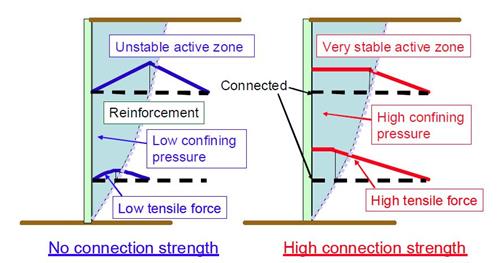
©F. Tatsuoka, O. Murata, and M. Tateyama
Figure 2. Illustration. Effects of facing connection condition on tensile force distribution in reinforcement.7
Yang et al. reported the behavior of a railway embankment wall constructed with a procedure similar to Japan Railway's RRR system. (See reference 42 and 7 through 9.) From measured maximum reinforcement strains in different layers, they conclude that the critical slip plane is likely curved, with the failure surface in the upper portion of the wall not deviating significantly from the 0.3H-distribution suggested by Schlosser and Long, and the slip plane in the lower portion of the wall being quite different from those of Rankine or Schlosser and Long.(43)
Perhaps the most extreme example to illustrate the deficiency concerning the critical slip planes is a full-scale experiment conducted by the Public Works Research Institute (PWRI), Japan. The experiment involves a 19.7-ft- (6-m-) high GRS wall with a segmental concrete blocks wall face, and the backfill was a sandy soil reinforced with six layers of 11.5-ft- (3.5-m-) long polymer grid. The reinforcement inside the wall was sequentially severed at pre-selected sections after construction of the wall was completed. Figure 3 shows the sequence of cutting the reinforcements, and figure 4 shows the maximum horizontal movement corresponding to cutting of the reinforcements. It is seen that there was little movement due to the cutting of the reinforcements until Cut No. 55. Any current design methods of reinforced soil walls would have predicted a failure condition to occur long before Cut No. 55. In a tieback design method, cutting reinforcement is equivalent to shortening the tieback lengths. The cuts before Cut No. 55 would have rendered the tiebacks far shorter than the anchorage needed in any tieback design method (e.g., AASHTO, FHWA, NCMA).
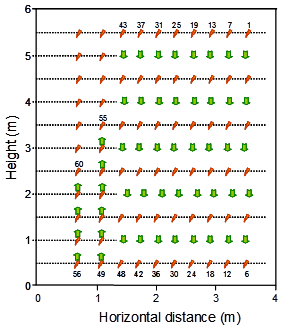
1 m = 3.28 ft
Figure 3. Illustration. Sequence of cutting of the PWRI test wall.
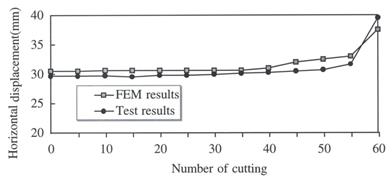
1 m = 3.28 ft
Figure 4. Chart. The resulting horizontal movement of the PWRI test wall.
From the standpoint of an internally stabilized retaining wall, the observed behavior is not at all surprising. A sheet of reinforcement, whether continuous or not, offers a similar restraining effect to lateral movement of soil, and hence will be able to achieve a stable composite. Note that the resulting stress distribution in the reinforcement will be rather different for continuous and discontinuous reinforcements. It should be noted that the observation of the PWRI experiment was supported by similar experiments by John in the United Kingdom and by the Amoco test wall in the United States.(44,25)
Lateral Earth Thrust Along Critical Slip Plane
Calculation of the driving force in pullout stability analysis involves determination of lateral thrusts along the critical slip plane. The FHWA NHI manual and AASHTO guidelines use Rankine active earth pressure for calculation of the driving force for GMSE walls with extensible reinforcement. The NCMA design manual uses Coulomb earth pressure for the calculation of the driving force.
Similar to AASHTO guideline, the British standard BS 8006 includes two methods for internal design of GMSE walls: the tieback wedge method and the coherent gravity method.(5) The former uses active earth pressure Ka for design; whereas the latter uses a K-value varying from the at-rest coefficient (Ko) to the active coefficient (Ka) in the upper 19.68 ft (6 m) of the wall, and Ka below 19.68 ft (6 m). The tieback wedge method is recommended when the short-term tensile strain exceeds 1 percent (e.g., polymeric reinforcement) while the coherent gravity method is recommended when the short-term tensile strain is less than 1 percent (e.g., steel reinforcement).
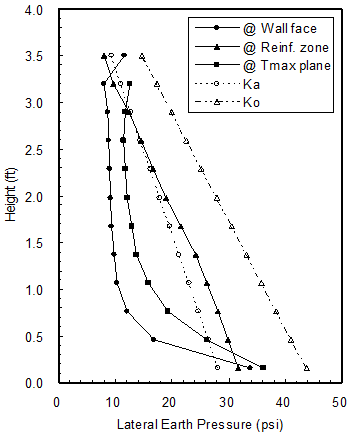
Chou and Wu conducted a study to investigate the performance of GRS walls with reinforcement at 0.98 ft (0.3 m) spacing by a sophisticated finite element code, DACSAR.(29) The lateral pressures and stresses along three separate sections were examined: earth pressure against wall face, earth pressure against the back of the reinforced soil mass, and lateral stresses along the plane of maximum tensile force in reinforcement, as shown in figure 5. The study showed that the lateral thrusts in the three sections are rather different. The lateral earth pressure, the smallest of the three, is nearly constant with depth except near the base of wall (where there is greater constraint to deformation). The lateral stresses along the plane of maximum reinforcement tensile force is almost parallel to the lateral earth pressure profile except the magnitude is somewhat larger. The study also showed that the earth pressure exerted on reinforced soil mass by the retained fill, i.e., the earth pressure commonly used for evaluation of external stability of reinforced soil walls, is close to the Rankine active earth pressure.
Pullout of reinforcement stems from the design concept of GMSE walls in which reinforcement serves as tiebacks. The reinforcement needs to be long enough to provide sufficient anchorage length to ensure internal stability of the reinforced zone of a GMSE wall or abutment. GRS walls/abutments, however, are designed based on a different concept. The reinforcement in a GRS structure serves to improve the stiffness and strength of the soil-reinforcement composite. Reinforcement length of a GRS wall is dictated by external stability. In a GRS wall, pullout of geosynthetic reinforcement is theoretically not a design issue.
©N.N. S. Chou and J.T.H. Wu
1 ft = .305 m
1 psi = 6.89 kPa
Figure 5. Chart. Lateral stress/pressure on different sections of a GRS.(29)
A very large number of pullout tests have been conducted by many researchers and designers to help assess pullout capacity of geosynthetic reinforcement under various conditions. It is important to point out that a great majority of the failures of reinforced soil walls involve prolonged rainfall (see references 35 and 45 through 50). In view of these findings, for design purposes, it will be prudent to conduct pullout tests under saturated undrained condition.
Observation of field performance of GRS walls and abutments with closely spaced reinforcement has strongly suggested that pullout is not a probable failure mode for closely spaced GRS walls. Even though pullout failure is not impossible in a reinforced soil wall, a single case of in-service reinforced soil wall where failure can be clearly attributed to pullout of reinforcement has not yet been identified. Nonetheless, the reinforced soil system does not know whether the reinforcement is designed as tiebacks (as in a GMSE) or a tensile inclusion to improve soil stiffness and strength (as in a GRS). In other words, the reinforcement in a GMSE wall, even though designed as tiebacks, also serves to improve the stiffness and strength of the sounding soil (although not as effectively because of the large reinforcement spacing); and conversely, the reinforcement in a GRS wall, even though designed as reinforcing inclusion, also serves as tiebacks. As a result, one can argue that it would not be a drawback to also check for pullout stability in the design of a GRS wall or abutment. Longer reinforcement length will likely lead to smaller lateral movement of a wall, unless the wall is in a "constrained fill" condition (where a firm sloping ground is behind the wall).(20)
The question then becomes: how to check for pullout failure if it is deemed warranted? The answer involves the knowledge of (a) the location of the critical slip plane in a reinforced soil mass and (b) the lateral thrust along the critical slip plane. The latter is less of an issue because the thrust can probably be assumed to be a combination of a Ka- or Ko-condition, depending on the desired degree of conservatism. The location of the critical slip plane, however, is a more troubling issue.
The location of the critical slip plane has traditionally been assumed to follow the Rankine theory. Based on studies by Tatsuoka and his associates, the location of a potential slip surface is a function of facing rigidity. The stiffer the facing, the closer the slip plane will be to the wall face.(41) Also, the location of the slip plane has been known to be affected by the loading condition on the wall crest. When a GRS wall is subject to large edge loads (as in an abutment), the critical slip plane is likely to be quite different from the Rankine active slip plane. The experiment performed by PWRI of Japan, as described previously under the subheading Critical Slip Plane, has further cast doubts on the applicability of the Rankine active slip plane. Also, it is possible that that such a slip plane does not exist for typical configurations, material properties, and loading conditions of GRS walls, as argued by Leshchinsky and Vulova.(40) As a final note, the NCHRP GRS test abutments with reinforcement spacing of 0.66 ft (0.2 m) and reinforcement length of 0.67H, and with loads being applied near the wall face, did not show any sign of geosynthetic pullout when loaded to failure. The reinforced soil mass clearly behaved as a coherent mass as it was subject to front edge loads all the way to failure. This further suggests that geosynthetic pullout is likely not a probable failure mode for closely spaced GRS abutments.
The inability to compute the driving force and resisting force with confidence may cast doubts on the usefulness for checking geosynthetic pullout of a GRS wall or abutment. Moreover, the method for checking pullout failure as adopted in current design guidelines is unrealistically conservative. The current design guidelines require that the pullout safety factor at each reinforcement layer be greater than a prescribed value (typically 1.5).(1,2,3) The fact is, pullout failure only occurs if a group of reinforcement layers experiences instability related to pullout. Pullout of any single reinforcement layer will never occur.
In summary, even though the extra design step of checking pullout failure will not harm the overall design of a GRS wall or abutment, two critical reasons-(a) pullout does not appear to be a probable failure mode, and (b) there is no reliable and realistic procedure for checking pullout-have rendered the reinforcement pullout check not particularly meaningful.