Synthesis of Geosynthetic Reinforced Soil (GRS) Design Topics

CHAPTER 4. ECCENTRICITY

As part of the design of conventional cantilever and gravity retaining walls with relatively rigid footings, overturning failure is commonly checked to determine whether the design meets the required margin of safety. This check typically consists of taking moments of all the stabilizing forces acting on the free body of the wall system about the toe (e.g., Point O for a cantilever wall shown in figure 6) and comparing them with the moments for the destabilizing forces about the same point. The required margin of safety for overturning is typically specified in the relevant code of practice.

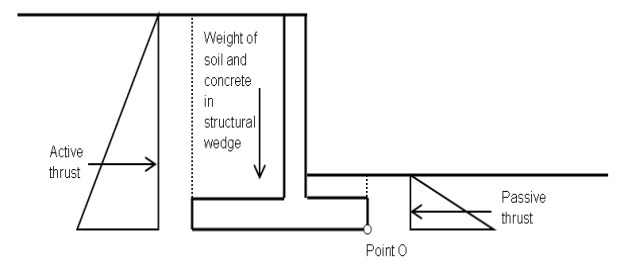
Figure 6. Drawing. Free body diagram, cantilever wall system for overturning calculations.

An alternative means of assessing the overturning potential of retaining walls has been proposed by the U.S. Army Corps of Engineers, (USACE).⁽⁵¹⁾ Rather than comparing the stabilizing and destabilizing moments, the overturning criteria are based on a minimum base area in compression, i.e., limiting the amount of footing "liftoff." This technical synopsis examines the purpose and theoretical justification of this design component.

ECCENTRICITY, BEARING PRESSURE DIAGRAM, AND FOOTING LIFTOFF

For a wall supported on a rigid concrete footing, the amount of footing liftoff is determined from its bearing pressure diagram. If R and R_v are the resultant force and vertical component of the resultant force, respectively, acting on the free body of the wall system per unit length, the bearing pressure diagram can be determined for several possible resultant force locations. Key to this evaluation is the estimation of the maximum (σ _max) and minimum (σ _min) bearing pressures, calculated using the equations shown in figure 7 and figure 8:

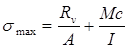
Figure 7. Equation. Estimated maximum bearing pressure, σ subscript max.

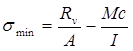
Figure 8. Equation. Estimated minimum bearing pressure, σ subscript min.

A equals the footing area, which is the footing width, B, per unit length for a plane strain problem. The distance from the centroid of footing to extreme fiber is c, which equals B/2. I is the moment of inertia of footing, and equals B³/12 per unit length. M is the moment about the footing centroid, and equals R_v times e, e being the eccentricity of the resultant force from the footing centroid. After simplifying, the equations in figure 7 and figure 8 become the equations in figure 9 and figure 10:

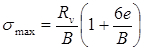
Figure 9. Equation. Simplified estimated maximum bearing pressure, σ subscript max.

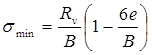
Figure 10. Equation. Simplified estimated minimum bearing pressure, σ subscript min.

For no footing liftoff, σ_min must be ≥ 0. By setting σ_min equal to 0 in the equation in figure 10, it can be seen that the resultant force acting on the free body of the wall system must lie within the middle third of the footing; i.e., e ≤ B/6.

As shown in the equation in figure 11, the point of action of the resultant force from the toe (χ_R) is calculated by simply summing the moments about the toe of all the forces acting on the free body of the wall system and dividing by the vector sum of the vertical force components acting on the footing (R_v).

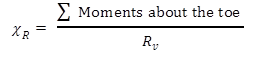
Figure 11. Equation. Resultant force from the toe, χ subscript R.

If the resultant force acts within the middle third, the bearing pressure diagram is trapezoidal and 100 percent of the footing is in compression; i.e., no liftoff (see figure 12). If the resultant force acts on the middle third point, the bearing pressure diagram is triangular and spans the entire footing width (figure 13). There is still no footing liftoff in this case. If the resultant force acts outside the middle third but within the footing, the bearing pressure diagram is also triangular but the span of the triangle is less than the footing width. The remaining portion of the bearing pressure diagram is negative; i.e.,σ_min < 0 (figure 14). The portion of the footing that is outside the triangular bearing pressure diagram (i.e., when σ < 0) is in a state of tension or liftoff. Clearly, it is undesirable to allow any footing liftoff except perhaps during temporary live loading or during extreme events such as earthquakes.

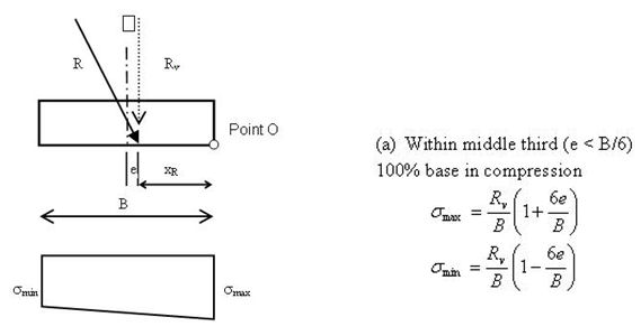
Figure 12. Drawing. Bearing pressure diagram, resultant force within middle third.

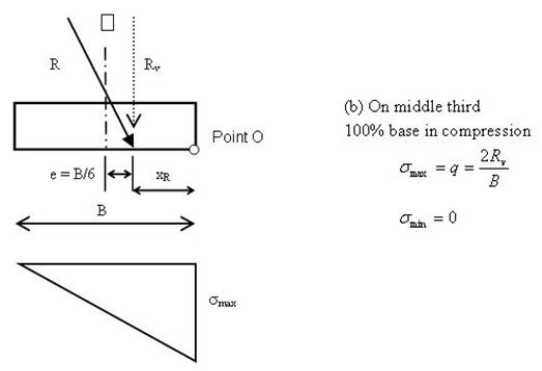
Figure 13. Drawing. Bearing pressure diagram, resultant force on middle third.

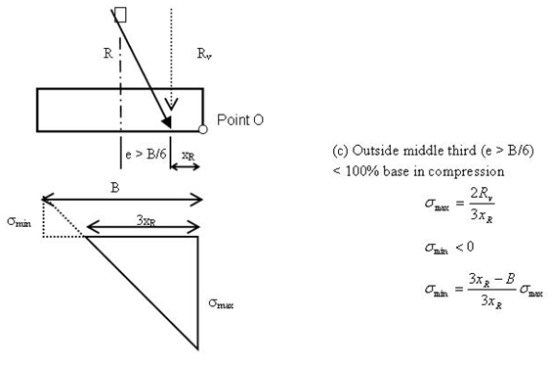
Figure 14. Drawing. Bearing pressure diagram, resultant force outside middle third.

The area of the footing in compression can be calculated by first computing the resultant ratio, RR, as shown in the equation in figure 15:

Figure 15. Equation. Resultant ratio, RR.

The percent area of footing in compression (A_fc) can be estimated as shown in the equation in figure 16:

Figure 16. Equation. Percent area of footing in compression, A subscript fc (in percent).

It follows that the percent area of footing experiencing liftoff is 100 percent minus A_fc.

If the resultant force acts at the toe of the footing, the wall is on the verge of overturning; i.e., the destabilizing moment is just equal to the stabilizing moment and there is no margin of safety available. If the resultant force acts outside the footing, the wall will overturn. The USACE requires that, in designing for earthquake protection, the resultant force must lie within the footing for retaining walls.⁽⁵¹⁾ The various possible scenarios described above are summarized in table 3.

Table 3 . Resultant force location and impact on safety against overturning, base area in compression, and bearing pressure diagram.

OVERTURNING VERSUS LIFTOFF

In this section, a simple methodology is presented to determine when liftoff will control. Figure 17 depicts the simple case of the lateral (E_a is horizontal because the wall friction δ is assumed to be 0) and vertical (W) forces acting on a rectangular wall with a rigid base.

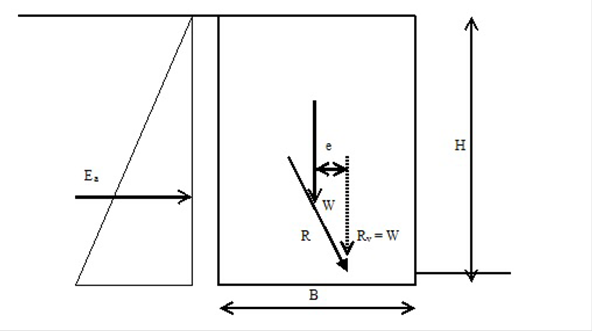
Figure 17. Drawing. Forces on a rectangular rigid wall.

The two forces-lateral and vertical-can be represented by a single resultant force, R, which is acting at an offset e from the centroid of the wall base. This eccentricity can be estimated by decomposing the resultant force into the vertical and horizontal (not shown) components at the base and summing moments about the centroid of the wall base as shown in the equation in figure 18:

Figure 18. Equation. Vertical component of resultant force at offset e, R_ve.

R_v is the vertical component of the resultant force, whose moment about the centroid of the wall base is not zero as opposed to the horizontal component. Therefore, the equation in figure 19 follows.

Figure 19. Equation. Force e.

The factor of safety against overturning can be obtained by summing moments about the toe as shown in the equation in figure 20:

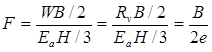
Figure 20. Equation. Safety factor, F.

Solving the equation in figure 20 for B gives the equation shown in figure 21:

Figure 21. Equation. Footing width, B.

For liftoff to occur, the condition shown in figure 22 must be satisfied.

Figure 22. Equation. Value of footing width B for liftoff to occur.

By inspecting the equations in figure 21 and figure 22, it can be determined that liftoff occurs when the factor of safety against overturning is less than 3; i.e., liftoff is not an issue when the overturning factor of safety exceeds 3. This criterion is only true when no surcharge loads are acting on top of the wall. When surcharge loads act on top of the wall (as is the case in a GRS IBS), then the factor of safety against overturning for no liftoff will be less than 3. How much less than 3 depends on the magnitude of the load on top of the wall and its point of action.

OVERTURNING DESIGN REQUIREMENTS FOR REINFORCED SOIL WALLS

• AASHTO.⁽⁵²⁾ In the 1998 AASHTO LRFD Bridge Design Specifications, the practice of calculating the ratio of stabilizing moment to overturning moment as a check for overturning of bridge abutments and GMSE walls was replaced by the resultant location criteria coupled with a check for bearing pressure. The criteria state that the resultant force for walls with footings on soil and rock must lie within the middle third and middle half, respectively, for allowable stress design (ASD) (middle half and middle three quarter for load and resistance factor design (LRFD)).
  
  
• FHWA.⁽⁵³⁾ FHWA 1997 guidelines for GMSE structures state that "the flexibility of MSE walls should make the potential for overturning failure highly unlikely." Unlike cantilever and gravity walls with relatively rigid footings, the base of GMSE or GRS walls have little or no flexural rigidity. The notion that they can support bending stresses with tensile contact pressures or liftoff developing seems counterintuitive and has not been observed in instrumented GMSE structures such as those studied by Simac et al. and Bathurst et al.^(54,55) Therefore, the FHWA 1997 guidelines omit overturning as a potential failure mode for GMSE structures. To control lateral deformation due to tilting, however, FHWA requires that the eccentricity of the resultant force be checked to determine whether it exceeds a maximum permissible value as prescribed by AASHTO.
  
  
• NCMA.⁽³⁾ NCMA indicates in its Design Manual for Segmental Retaining Walls (these are geosynthetic reinforced walls that use dry stacked interlocking modular masonry concrete units as a facing) that overturning about the toe should be considered as a potential failure mechanism, a view that differs from that of the FHWA. NCMA does not require consideration of the base eccentricity criteria.
  
  
• Canadian Geotechnical Society.⁽⁵⁶⁾ Like the NCMA, the Canadian Foundation Engineering Manual (Canadian Geotechnical Society, 2006) does require checking for overturning of reinforced walls.
  
  
• British Standards Institution.⁽⁵⁾ British standard BS 8006 (1995) does not require overturning of strengthened/reinforced soil and other fills be assessed during design. For external stability, the British standard does require a check for bearing capacity, sliding, and external slip. In checking for bearing capacity, the maximum bearing pressure (σ_max) is compared with the bearing capacity. Because σ_max increases with increasing eccentricity, the implication is that the eccentricity will be automatically limited by imposing a limit on the bearing capacity.
  
  
• Designing With Geosynthetics.⁽⁵⁷⁾ Koerner indicated that the factor of safety against overturning for geotextile reinforced walls is typically very high. He further points out that overturning is not a likely failure mechanism because of base flexibility. Therefore, "many engineers do not even include an overturning calculation in the design process."
  
  
• Retaining Wall-Dialog: "A Tale of Two Walls" and "GRS-A New Era in Reinforced Soil Technology."^(58,59) Barrett and Ruckman presented cases of GRS walls with negative batter being used or tested successfully in Colorado (figure 23), New Zealand (figure 24), Japan (figure 25), and elsewhere. Barrett wrote "prevailing guidelines for internally supported MSE walls are based on translations from externally supported cantilever walls and are generally inappropriate." GRS walls with negative batter that generally do not meet the overturning requirements are still performing well today.

Source: R.K. Barrett and A.C. Ruckman
Figure 23. Photo. First negative batter GRS wall constructed in Colorado for the CDOT. ⁽⁵⁹⁾

Source: R.K. Barrett and A.C. Ruckman
Figure 24. Photo. GRS wall in New Zealand with a negative. ⁽⁵⁹⁾

Source: R.K. Barrett and A.C. Ruckman
Figure 25. Photo. Research on negative batter GRS walls in Japan. ⁽⁵⁹⁾

SUMMARY

Table 4 offers key points relating to the need to limit the eccentricity in the design of GRS walls.

Table 4 . Key points relating to the need to limit the eccentricity in the design of GRS walls.

GMSE = Geosynthetic Mechanically Stabilized Earth
GRS = Geosynthetic Reinforced Soil

Clearly, checking for limiting eccentricity is generally prudent. However, such a check is based on theories that really do not apply to flexible base systems. The check is intended as a failure mechanism that is feasibly impossible in a GRS and thus should be discontinued.