LTPP Computed Parameter: Dynamic Modulus

HTML Version of Errata for FHWA-HRT-10-035

PDF Version of Errata (84.0 KB)

PDF files can be viewed with the Acrobat® Reader®

FOREWORD

The dynamic modulus, |E*|, is a fundamental property that defines the strain response characteristics of asphalt concrete mixtures as a function of loading rate and temperature. The significance of this material property is threefold. First, it is one of the primary material property inputs in the Mechanistic Empirical Pavement Design Guide (MEPDG) and software developed by National Cooperative Highway Research Program Project 1-37A.^(1,2) MEPDG uses a master curve and time-temperature shift factors in its internal modulus computation.⁽¹⁾ In MEPDG, the master curve is constructed using a hierarchical structure of inputs ranging from estimates based on mixture volumetrics and binder tests to full-scale mixture |E*| testing. |E*| is one of the primary properties measured in the Asphalt Mixture Performance Test protocol that complements the volumetric mix design.^(3,4) Additionally, it is one of the fundamental linear viscoelastic material properties that can be used in advanced pavement response models based on viscoelasticity.

Given the significance of |E*|, this study evaluated existing prediction models, developed new models, and populated the Long-Term Pavement Performance database to provide a valuable data source for the pavement community. Supplementing the full suite of material properties, performance history, traffic, and climate with |E*| estimates will be advantageous in conducting MEPDG calibration, validation, and implementation.

Jorge E. Pagán-Ortiz
Director, Office of Infrastructure
Research and Development

Technical Report Documentation Page

SI* (Modern Metric) Conversion Factors

*SI is the symbol for the International System of Units. Appropriate rounding should be made to comply with Section 4 of ASTM E380.
(Revised March 2003)

TABLE OF CONTENTS

• EXECUTIVE SUMMARY
• 1.0 INTRODUCTION
• 2.0 PREDICTIVE MODELS
  • 2.1 ORIGINAL WITCZAK EQUATION (NCHRP 1-37A)
  • 2.2 MODIFIED WITCZAK EQUATION BASED ON |G*| (NCHRP 1-40D)
  • 2.3 HIRSCH MODEL
  • 2.4 LAW OF MIXTURES PARALLEL MODEL (AL-KHATEEB MODEL)
  • 2.5 ANN MODELS
  • 2.6 SUMMARY OF INPUT VARIABLES
• 3.0 DATABASES
  • 3.1 STATEMENT OF NEED
    • 3.1.1 Inconsistent Definition of Frequency
    • 3.1.2 Use of Estimated |G*| Values
    • 3.1.3 Low-Temperature |G*| Values
    • 3.1.4 Aging Effects
  • 3.2 BINDER DATABASES
    • 3.2.1 Witczak Binder Database
    • 3.2.2 FHWA Mobile Trailer Binder Database
    • 3.2.3 FHWA TPF-5(019) Binder Database
    • 3.2.4 NCDOT Binder Database
    • 3.2.5 Citgo Binder Database
    • 3.2.6 WRI Binder Database
  • 3.3 MIXTURE DATABASES
    • 3.3.1 Witczak Mixture Database
    • 3.3.2 FHWA Mobile Trailer Mixture Database
    • 3.3.3 FHA TPF-5(019) Mixture Database
    • 3.3.4 NCDOT Mixture Database
    • 3.3.5 WRI Mixture Database
    • 3.3.6 Citgo Mixture Database
    • 3.3.7 FHWA M_R Database
    • 3.3.8 LTPP Data
    • 3.3.9 Input Source Hierarchy
    • 3.3.10 Data Structure and Detail
• 4.0 EVALUATION OF |E*| PREDICTIVE MODELS
  • 4.1 ANN STRUCTURE USED IN THIS STUDY
  • 4.2 EVALUATION OF BINDER |G*|-BASED MODELS
  • 4.3 VISCOSITY-BASED ANN
• 5.0 ANN MODELS FOR POPULATING THE LTPP DATABASE
  • 5.1 M_R ANN MODEL
    • 5.1.1 Forward Modeling
    • 5.1.2 ANN Model |E*| Backcalculation
  • 5.2 VV ANN MODEL
  • 5.3 GV ANN MODEL
  • 5.4 OTHER ANN MODELS
  • 5.5 ERROR ASSESSMENT
• 6.0 PREDICTION OF |E*| FOR LTPP LAYERS
  • 6.1 MODEL PRIORITIZATION AND DECISION TREE DEVELOPMENT
  • 6.2 DATA QC
    • 6.2.1 QC #1
    • 6.2.2 QC #2
    • 6.2.3 QC #3
    • 6.2.4 QC #4
    • 6.2.5 QC #5
    • 6.2.6 QC #6
    • 6.2.7 QC #7
  • 6.3 CONTRACTOR JUDGMENT
  • 6.4 CONTRACTOR MASTERCURVE JUDGMENT
  • 6.5 PREDICTION STATISTICS
  • 6.6 LTPP DATABASE ADDITIONS
• 7.0 SUMMARY AND FUTURE WORK
• APPENDIX A: PROCESSING ASPHALT BINDER VISCOSITY DATA
  • A.1 INTRODUCTION
  • A.2 TEMPERATURE SUSCEPTIBILITY RELATIONSHIP
  • A.3 R&BT TEMPERATURE
  • A.4 PENETRATION
  • A.5 ABSOLUTE VISCOSITY
  • A.6 KINEMATIC VISCOSITY
  • A.7 EXAMPLE PROBLEM
  • A.8 TYPICAL VALUES FOR PURCHASE SPECIFICATION GRADE
• APPENDIX B: PROCESSING ASPHALT BINDER SHEAR MODULUS DATA
  • B.1 INTRODUCTION
  • B.2 USE OF BRR DATA IN |G*\ MASTERCURVE GENERATION
  • B.3 ANALYSIS USING DSR MEASUREMENTS
  • B.4 ANALYSIS WITH BBR MEASUREMENTS
  • B.5 COMBINING DSR AND BBR ANALYSIS RESULTS
  • B.6 COMPARISON OF RESULTS WITH AND WITHOUT BBR MEASUREMENTS
  • B.7 EXTRACTING FULL BINDER |G*| DATA FROM LIMITED ISOCHRONAL MEASUREMENTS
  • B.8 t-T SHIFT FACTOR SURROGATE MODEL DEVELOPMENT
    • B.8.1 Phenomenological t-T Shift Factor Function Model
    • B.8.2 Use of Average t-T Shift Factor Function
  • B.9 INCLUSION OF BBR DATA IN MASTERCURVE GENERATION
  • B.10 PAV- TO RTFO-AGING MODEL (PAR MODEL)
  • B.11 AGING EFFECT ON M-VALUE
  • B.12 VERIFICATION OF LIMITED DATA DEVELOPMENT
    • B.12.1 Level 1a Verification
    • B.12.2 Level 1b Verification
    • B.12.3 Level 2 Verification
    • B.12.4 Level 3 Verification
• APPENDIX C: AMPT VERSUS TP-62
  • C.1 EXPERIMENTAL VERIFICATION OF AMPT AND TP-62 DIFFERENCES
  • C.2 COMPARISON OF AMPT AND TP-62 PROTOCOLS WITH THE AVAILABLE DATABASE
  • C.3 EVALUATION OF AMPT VERSUS TP-62 PROTOCOLS USING ANN MODEL
• APPENDIX D: ANN MODEL FACTORS
  • D.1 INTRODUCTION
  • D.2 M_R ANN
  • D.3 VV ANN
  • D.4 |G*|-BASED ANN (GV ANN)
• APPENDIX E: ANNACAP SOFTWARE MANUAL
  • E.1 INTRODUCTION
  • E.2 DISCLAIMER
  • E.3 INSTALLATION INSTRUCTIONS
  • E.4 USING ANNACAP
    • E.4.1 Program Main Screen
    • E.4.2 Input Data
    • E.4.3 Layer ID
    • E.4.4 M_R-Based ANN
    • E.4.5 |G*|-Based ANN
    • E.4.6 Viscosity-Based ANN
  • E.5 BATCH MODE
  • E.6 OUTPUT DIRECTORY
  • E.7 RUN ANALYSIS
  • E.8 FORM OF SUPPLEMENTARY FUNCTIONS
    • E.8.1 CAM Model Function
  • E.9 TIME-TEMPERATURE SHIFT FACTOR FUNCTION FOR |G*|
    • E.9.1 Level 1 (WLF Function)
    • E.9.2 Levels 2 and 3
  • E.10 SIGMOIDAL FUNCTION
  • E.11 TIME-TEMPERATURE SHIFT FACTOR FUNCTION FOR |E*|
• REFERENCES

LIST OF FIGURES

• Figure 1. Illustration. Modulus prediction model decision tree.
• Figure 2. Graph. Comparison between the Witczak predictive model and measured |G*|_b values in arithmetic scale.
• Figure 3. Graph. Comparison between the Witczak predictive model and measured |G*|_b values in logarithmic scale.
• Figure 4. Graph. Comparison between the Witczak predictive model and measured to develop the model
• Figure 5. Graph. Comparison between the Witczak predictive model and measured |G*|_b values using Citgo binders in the North Carolina Department of Transportation (NCDOT) database in arithmetic scale.
• Figure 6. Graph. Comparison between the Witczak predictive model and measured |G*|_b values using Citgo binders in the NCDOT database in logarithmic scale.
• Figure 7. Graph. Prediction of the processed Witczak, FHWA I, FHWA II, NCDOT I, NCDOT II, WRI, and Citgo databases using the modified Witczak in arithmetic scale.
• Figure 8. Graph. Prediction of the processed Witczak, FHWA I, FHWA II, NCDOT I, NCDOT II, WRI, and Citgo databases using the modified Witczak in logarithmic scale.
• Figure 9. Graph. Prediction of the processed Witczak, FHWA I, FHWA II, NCDOT I, NCDOT II, WRI, and Citgo databases using the Hirsch model in arithmetic scale.
• Figure 10. Graph. Prediction of the processed Witczak, FHWA I, FHWA II, NCDOT I, NCDOT II, WRI, and Citgo databases using the Hirsch model in logarithmic scale.
• Figure 11. Graph. Prediction of the processed Witczak, FHWA I, FHWA II, NCDOT I, NCDOT II, WRI, and Citgo databases using the Al-Khateeb model in arithmetic scale.
• Figure 12. Graph. Prediction of the processed Witczak, FHWA I, FHWA II, NCDOT I, NCDOT II, WRI, and Citgo databases using the Al-Khateeb model in logarithmic scale.
• Figure 13. Graph. Prediction of training data containing processed Witczak, FHWA I, NCDOT I, and WRI databases using |G*| binder and gradation-based pilot ANN model (G-GR pANN) in arithmetic scale.
• Figure 14. Graph. Prediction of training data containing processed Witczak, FHWA I, NCDOT I, and WRI databases using G-GR pANN in logarithmic scale.
• Figure 15. Graph. Prediction of training data containing processed Witczak, FHWA I, NCDOT I, and WRI databases using preliminary |G*|-based models used in phase I of the study (G-V) pANN in arithmetic scale.
• Figure 16. Graph. Prediction of training data containing processed Witczak, FHWA I, NCDOT I, and WRI databases using G-V pANN in logarithmic scale.
• Figure 17. Graph. Predicted moduli using G-GR pANN and modified Witczak models for the FHWA II database in arithmetic scale.
• Figure 18. Graph. Predicted moduli using G-GR pANN and modified Witczak models for the FHWA II database in logarithmic scale.
• Figure 19. Graph. Predicted moduli using G-V pANN and Hirsch models for the FHWA II database in arithmetic scale.
• Figure 20. Graph. Predicted moduli using G-V pANN and Hirsch models for the FHWA II database in logarithmic scale.
• Figure 21. Graph. Predicted moduli using G-GR pANN and modified Witczak models for the NCDOT II database in arithmetic scale.
• Figure 22. Graph. Predicted moduli using G-GR pANN and modified Witczak models for the NCDOT II database in logarithmic scale.
• Figure 23. Graph. Predicted moduli using G-V pANN and Hirsch models for the NCDOT II database in arithmetic scale.
• Figure 24. Graph. Predicted moduli using G-V pANN and Hirsch models for the NCDOT II database in logarithmic scale.
• Figure 25. Graph. Predicted moduli using G-GR pANN and modified Witczak models for the Citgo database in arithmetic scale.
• Figure 26. Graph. Predicted moduli using G-GR pANN and modified Witczak models for the Citgo database in logarithmic scale.
• Figure 27. Graph. Predicted moduli using G-V pANN and Hirsch models for the Citgo database in arithmetic scale.
• Figure 28. Graph. Predicted moduli using G-V pANN and Hirsch models for the Citgo database in logarithmic scale.
• Figure 29. Graph. Prediction of training data containing Witczak, FHWA I, and NCDOT I databases using Visc-GR pANN in arithmetic scale.
• Figure 30. Graph. Prediction of training data containing Witczak, FHWA I, and NCDOT I databases using Visc-GR pANN in logarithmic scale.
• Figure 31. Graph. Prediction of training data containing Witczak, FHWA I, and NCDOT I databases using Visc-V pANN in arithmetic scale.
• Figure 32. Graph. Prediction of training data containing Witczak, FHWA I, and NCDOT I databases using Visc-V pANN in logarithmic scale.
• Figure 33. Graph. Predicted moduli using Visc-GR pANN model for the FHWA II database in arithmetic scale.
• Figure 34. Graph. Predicted moduli using Visc-GR pANN model for the FHWA II database in logarithmic scale.
• Figure 35. Graph. Predicted moduli using Visc-V pANN model for the FHWA II database in arithmetic scale.
• Figure 36. Graph. Predicted moduli using Visc-V pANN model for the FHWA II database in logarithmic scale.
• Figure 37. Graph. Predicted moduli using Visc-GR pANN model for the NCDOT II database in arithmetic scale.
• Figure 38. Graph. Predicted moduli using Visc-GR pANN model for the NCDOT II database in logarithmic scale.
• Figure 39. Graph. Predicted moduli using Visc-V pANN model for the NCDOT II database in arithmetic scale.
• Figure 40. Graph. Predicted moduli using Visc-V pANN model for the NCDOT II database in logarithmic scale.
• Figure 41. Illustration. Network structure used for training the ANN models.
• Figure 42. Illustration. Stress distribution in the IDT specimen subjected to a strip load.
• Figure 43. Graph. Poisson's ratio versus reduced time for S12.5C.
• Figure 44. Graph. Comparison of predicted and measured M_R values for S12.5C mixture.
• Figure 45. Graph. Comparison of predicted and measured M_R values for S12.5CM mixture.
• Figure 46. Graph. Comparison of predicted and measured M_R values for S12.5FE mixture.
• Figure 47. Graph. Comparison of predicted and measured M_R values for B25.0C mixture.
• Figure 48. Graph. M_R ANN model using 90 percent of randomly selected data as a training set in arithmetic scale.
• Figure 49. Graph. M_R ANN model using 90 percent of randomly selected data as a training set in logarithmic scale.
• Figure 50. Graph. M_R ANN model using 10 percent of randomly selected data as a verification set in arithmetic scale.
• Figure 51. Graph. M_R ANN model using 10 percent of randomly selected data as a verification set in logarithmic scale.
• Figure 52. Graph. VV ANN model using 90 percent of randomly selected data as a training set in arithmetic scale.
• Figure 53. Graph. VV ANN model using 90 percent of randomly selected data as a training set in logarithmic scale.
• Figure 54. Graph. VV ANN model using 10 percent of randomly selected data as a verification set in arithmetic scale.
• Figure 55. Graph. VV ANN model using 10 percent of randomly selected data as a verification set in logarithmic scale.
• Figure 56. Graph. GV ANN model using 90 percent of randomly selected data as a training set in arithmetic scale.
• Figure 57. Graph. GV ANN model using 90 percent of randomly selected data as a training set in logarithmic scale.
• Figure 58. Graph. GV ANN model using 10 percent of randomly selected data as a verification set in arithmetic scale.
• Figure 59. Graph. GV ANN model using 10 percent of randomly selected data as a verification set in logarithmic scale.
• Figure 60. Illustration. Decision tree applied to population of LTPP database based on ranking of ANN models.
• Figure 61. Graph. Example of the effect of a violation of QC #1 for M_R ANN model in semi-log scale.
• Figure 62. Graph. Example of the effect of a violation of QC #1 for M_R ANN model in log-log scale.
• Figure 63. Graph. Example of the effect of a violation of QC #1 for VV ANN model in semi-log scale.
• Figure 64. Graph. Example of the effect of a violation of QC #1 for VV ANN model in log-log scale.
• Figure 65. Graph. Example of the effect of a violation of QC #1 for VV ANN model unshifted data.
• Figure 66. Graph. Example of the effect of a violation of QC #2 in semi-log scale.
• Figure 67. Graph. Example of the effect of a violation of QC #2 in log-log scale.
• Figure 68. Graph. Example of the effect of a violation of QC #2 unshifted data.
• Figure 69. Graph. Example of the effect of a violation of QC #3 in semi-log scale.
• Figure 70. Graph. Example of the effect of a violation of QC #3 in log-log scale.
• Figure 71. Graph. Example of the effect of a violation of QC #3 unshifted data.
• Figure 72. Graph. Example of the effect of a violation of QC #4 in semi-log scale.
• Figure 73. Graph. Example of the effect of a violation of QC #4 in log-log scale.
• Figure 74. Graph. Example of the effect of a violation of QC #4 unshifted data.
• Figure 75. Graph. Example of the effect of a violation of QC #5 in semi-log scale.
• Figure 76. Graph. Example of the effect of a violation of QC #5 in log-log scale.
• Figure 77. Graph. Example of the effect of a violation of QC #5 unshifted data.
• Figure 78. Illustration. ANN models and their appropriate input and output tables.
• Figure 79. Graph. A-VTS relationship.
• Figure 80. Graph. |G*| versus frequency curves at different temperatures.
• Figure 81. Graph. |G*| versus reduced frequency mastercurve at 59 °F (15 °C)
• Figure 82. Graph. t-T shift factor function at 59 °F (15 °C)
• Figure 83. Graph. D(t) at different temperatures for ALF AC5 binder
• Figure 84. Graph. Comparison of optimization and regression GPL characterization results.
• Figure 85. Graph. |G*| mastercurve for the WesTrack binder at 59 °F (15 °C)
• Figure 86. Graph. Optimized t-T shift function for WesTrack binder at 59 °F (15 °C)
• Figure 87. Graph. Comparison of t-T shift factor functions calibrated with and without BBR data.
• Figure 88. Graph. |G*| mastercurve using t-T shift factor function calibrated without BBR data.
• Figure 89. Graph. |G*| mastercurves characterized with and without BBR data for ALF AC5 binder
• Figure 90. Graph. |G*| mastercurves characterized with and without BBR data for the MnRoad Pen 120-150 binder
• Figure 91. Graph. |G*| mastercurves characterized with and without BBR data for the WesTrack binder
• Figure 92. Graph. t-T shift factor function characterized with and without BBR data for the ALF AC5 binder
• Figure 93. Graph. t-T shift factor function characterized with and without BBR data for the MnRoad Pen 120-150 binder
• Figure 94. Graph. t-T shift factor function characterized with and without BBR data for the WesTrack binder
• Figure 95. Graph. Phenomenological t-T shift factor function.
• Figure 96. Graph. Effect of change in time from DSR to BBR on the t-T shift factor function model
• Figure 97. Graph. t-T shift factor model verification with phenomenological model
• Figure 98. Graph. Average t-T shift factor function.
• Figure 99. Graph. t-T shift factor model verification with average function model
• Figure 100. Graph. Effect of temperature on aging ratio of asphalt binder
• Figure 101. Graph. Effect of angular frequency on aging ratio of asphalt binder
• Figure 102. Graph. Calibrated PAR model in arithmetic scale.
• Figure 103. Graph. Calibrated PAR model in logarithmic scale.
• Figure 104. Graph. Strength of PAR model in arithmetic scale.
• Figure 105. Graph. Strength of PAR model in logarithmic scale.
• Figure 106. Graph. PAR model verification in arithmetic logarithmic scale.
• Figure 107. Graph. PAR model verification in logarithmic scale.
• Figure 108. Graph. BBR-calibrated k_T relationship.
• Figure 109. Graph. Comparison of |G*| mastercurve analysis under PAV and RTFO conditions for ALF AC10 binder
• Figure 110. Graph. Calibrated PAR model for BBR conditions in arithmetic scale.
• Figure 111. Graph. Calibrated PAR model for BBR conditions in logarithmic scale.
• Figure 112. Graph. Verification of m-value relationship.
• Figure 113. Graph. Comparison of typical |G*| mastercurves characterized using full database and Superpave™ only database.
• Figure 114. Graph. Comparison of typical t-T shift factors characterized using full database and Superpave™ only database.
• Figure 115. Graph. Level 1a verification of limited data analysis procedure in arithmetic scale using phenomenological shift factor function model
• Figure 116. Graph. Level 1a verification of limited data analysis procedure in logarithmic scale using phenomenological shift factor function model
• Figure 117. Graph. Level 1a verification of limited data analysis procedure in arithmetic scale using average shift factor function model
• Figure 118. Graph. Level 1a verification of limited data analysis procedure in logarithmic scale using average shift factor function model
• Figure 119. Graph. Comparison of typical |G*| mastercurve characterized using full database and Superpave™ only database plus PAR model
• Figure 120. Graph. Comparison of typical t-T shift factors characterized using full database and Superpave™ only database plus PAR model
• Figure 121. Graph. Level 1b verification of limited data analysis procedure in arithmetic scale using phenomenological shift factor function model
• Figure 122. Graph. Level 1b verification of limited data analysis procedure in logarithmic scale using phenomenological shift factor function model
• Figure 123. Graph. Level 1b verification of limited data analysis procedure in arithmetic scale using average shift factor function model
• Figure 124. Graph. Level 1b verification of limited data analysis procedure in logarithmic scale using average shift factor function model
• Figure 125. Graph. Level 2 verification of limited data analysis procedure in arithmetic scale using phenomenological shift factor function model
• Figure 126. Graph. Level 2 verification of limited data analysis procedure in logarithmic scale using phenomenological shift factor function model
• Figure 127. Graph. Level 2 verification of limited data analysis procedure in arithmetic scale using average shift factor function model
• Figure 128. Graph. Level 2 verification of limited data analysis procedure in logarithmic scale using average shift factor function model
• Figure 129. Graph. Level 3 verification of limited data analysis procedure in arithmetic scale using phenomenological shift factor function model
• Figure 130. Graph. Level 3 verification of limited data analysis procedure in logarithmic scale using phenomenological shift factor function model
• Figure 131. Graph. Level 3 verification of limited data analysis procedure in arithmetic scale using average shift factor function model
• Figure 132. Graph. Level 3 verification of limited data analysis procedure in logarithmic scale using average shift factor function model
• Figure 133. Graph. Test mixture gradation.
• Figure 134. Graph. Comparison of |E*| measured via AMPT and TP-62 protocols in arithmetic scale.
• Figure 135. Graph. Comparison of |E*| measured via AMPT and TP-62 protocols in logarithmic scale.
• Figure 136. Graph. Frequency distribution of temperature in AMPT versus TP-62 databases.
• Figure 137. Graph. Range of temperature in AMPT versus TP-62 databases.
• Figure 138. Graph. Frequency distribution of frequency in AMPT versus TP-62 databases.
• Figure 139. Graph. Range of loading frequency in AMPT versus TP-62 databases.
• Figure 140. Graph. Frequency distribution of percentage retained on ¾-inch (19.05-mm) sieve (_ρ¾) in AMPT versus TP-62 databases.
• Figure 141. Graph. Range of percentage retained on ¾-inch (19.05-mm) sieve (_ρ¾) in AMPT versus TP-62 databases.
• Figure 142. Graph. Frequency distribution of percentage retained on ³/₈-inch (9.56-mm) sieve (_ρ3/8) in AMPT versus TP-62 databases.
• Figure 143. Graph. Range of percentage retained on ³/₈-inch (9.56-mm) sieve (_ρ3/8) in AMPT versus TP-62 databases.
• Figure 144. Graph. Frequency distribution of percentage retained on #4 sieve (_ρ4) in AMPT versus TP-62 databases.
• Figure 145. Graph. Range of percentage retained on #4 sieve (_ρ4) in AMPT versus TP-62 databases.
• Figure 146. Graph. Frequency distribution of percentage passing #200 sieve (_ρ200) in AMPT versus TP-62 databases.
• Figure 147. Graph. Range of percentage passing #200 sieve (_ρ200) in AMPT versus TP-62 databases.
• Figure 148. Graph. Frequency distribution of specimen air voids in AMPT versus TP-62 databases.
• Figure 149. Graph. Range of specimen air voids in AMPT versus TP-62 databases.
• Figure 150. Graph. Frequency distribution of effective binder volume in AMPT versus TP-62 databases.
• Figure 151. Graph. Range of effective binder volume in AMPT versus TP-62 databases.
• Figure 152. Graph. Frequency distribution of VMA in AMPT versus TP-62 databases.
• Figure 153. Graph. Range of VMA in AMPT versus TP-62 databases.
• Figure 154. Graph. Frequency distribution of VFA in AMPT versus TP-62 databases.
• Figure 155. Graph. Range of  VFA in AMPT versus TP-62 databases.
• Figure 156. Graph. Frequency distribution of |G*| in AMPT versus TP-62 databases.
• Figure 157. Range of |G*| in AMPT versus TP-62 databases.
• Figure 158. Graph. Percentage of difference between AMPT versus TP-62 databases based on similar ranges of different variables at 39.9 °F (4.4 °C)
• Figure 159. Graph. Percentage of difference between AMPT versus TP-62 databases based on similar ranges of different variables at 69.9 °F (21.1 °C)
• Figure 160. Graph. Percentage of difference between AMPT versus TP-62 databases based on similar ranges of different variables at 100 °F (37.8 °C)
• Figure 161. Graph. Percentage of difference between AMPT versus TP-62 databases based on similar ranges of different variables at 129.2 °F (54.0 °C)
• Figure 162. Graph. Percentage of difference between AMPT versus TP-62 databases based on similar ranges of different variables at 129.9 °F (54.4 °C)
• Figure 163. Graph. Prediction of the combination of AMPT and TP-62 data using the modified Witczak and G-GR pANN models in arithmetic scale.
• Figure 164. Graph. Prediction of the combination of AMPT and TP-62 data using the modified Witczak and G-GR pANN models in logarithmic scale.
• Figure 165. Graph. Prediction of the combination of AMPT and TP-62 data using the Hirsch model in arithmetic scale.
• Figure 166. Graph. Prediction of the combination of AMPT and TP-62 data using the Hirsch model in logarithmic scale.
• Figure 167. Graph. Prediction of the combination of AMPT and TP-62 data using the Al-Khateeb model in arithmetic scale.
• Figure 168. Graph. Prediction of the combination of AMPT and TP-62 data using the Al-Khateeb model in logarithmic scale.
• Figure 169. Graph. Prediction of the AMPT data using the modified Witczak and AMPT pANN models in arithmetic scale.
• Figure 170. Graph. Prediction of the AMPT data using the modified Witczak and AMPT pANN models in logarithmic scale.
• Figure 171. Graph. Prediction of the AMPT data using the Hirsch model in arithmetic scale.
• Figure 172. Graph. Prediction of the AMPT data using the Hirsch model in logarithmic scale.
• Figure 173. Graph. Prediction of the AMPT data using the Al-Khateeb model in arithmetic scale.
• Figure 174. Graph. Prediction of the AMPT data using the Al-Khateeb model in logarithmic scale.
• Figure 175. Graph. Prediction of the TP-62 data using the modified Witczak and TP-62 pANN models in arithmetic scale.
• Figure 176. Graph. Prediction of the TP-62 data using the modified Witczak and TP-62 pANN models in logarithmic scale.
• Figure 177. Graph. Prediction of the TP-62 data using the Hirsch model in arithmetic scale.
• Figure 178. Graph. Prediction of the TP-62 data using the Hirsch model in logarithmic scale.
• Figure 179. Graph. Prediction of the TP-62 data using the Al-Khateeb model in arithmetic scale.
• Figure 180. Graph. Prediction of the TP-62 data using the Al-Khateeb model in logarithmic scale.
• Figure 181. Graph. Prediction of the FHWA II data using the modified Witczak and G-GR pANN models in arithmetic scale.
• Figure 182. Graph. Prediction of the FHWA II data using the modified Witczak and G-GR pANN models in logarithmic scale.
• Figure 183. Graph. Prediction of the FHWA II data using the AMPT pANN and TP-62 pANN models in arithmetic scale.
• Figure 184. Graph. Prediction of the FHWA II data using the AMPT pANN and TP-62 pANN models in logarithmic scale.
• Figure 185. Graph. Prediction of the FHWA II data using the Hirsch model in arithmetic scale.
• Figure 186. Graph. Prediction of the FHWA II data using the Hirsch model in logarithmic scale.
• Figure 187. Graph. Prediction of the FHWA II data using the Al-Khateeb model in arithmetic scale.
• Figure 188. Graph. Prediction of the FHWA II data using the Al-Khateeb model in logarithmic scale.
• Figure 189. Graph. Prediction of the NCDOT II data using the modified Witczak and  G-GR pANN models in arithmetic scale.
• Figure 190. Graph. Prediction of the NCDOT II data using the modified Witczak and  G-GR pANN models in logarithmic scale.
• Figure 191. Graph. Prediction of the NCDOT II data using the AMPT pANN and TP-62 pANN models in arithmetic scale.
• Figure 192. Graph. Prediction of the NCDOT II data using the AMPT pANN and TP-62 pANN models in logarithmic scale.
• Figure 193. Graph. Prediction of the NCDOT II data using the Hirsch model in arithmetic scale.
• Figure 194. Graph. Prediction of the NCDOT II data using the Hirsch model in logarithmic scale.
• Figure 195. Graph. Prediction of the NCDOT II data using the Al-Khateeb model in arithmetic scale.
• Figure 196. Graph. Prediction of the NCDOT II data using the Al-Khateeb model in logarithmic scale.
• Figure 197. Graph. Prediction of the Citgo data using the modified Witczak and G-GR pANN models in arithmetic scale.
• Figure 198. Graph. Prediction of the Citgo data using the modified Witczak and G-GR pANN models in logarithmic scale.
• Figure 199. Graph. Prediction of the Citgo data using the AMPT pANN and TP-62 pANN models in arithmetic scale.
• Figure 200. Graph. Prediction of the Citgo data using the AMPT pANN and TP-62 pANN models in logarithmic scale.
• Figure 201. Graph. Prediction of the Citgo data using the Hirsch model in arithmetic scale.
• Figure 202. Graph. Prediction of the Citgo data using the Hirsch model in logarithmic scale.
• Figure 203. Graph. Prediction of the Citgo data using the Al-Khateeb model in arithmetic scale.
• Figure 204. Graph. Prediction of the Citgo data using the Al-Khateeb model in logarithmic scale.
• Figure 205. Screenshot. ANNACAP main screen.
• Figure 206. Illustration. ANNACAP menu diagram.
• Figure 207. Screenshot. ANNACAP input screen.
• Figure 208. Screenshot. Output directory dialog.
• Figure 209. Screenshot. Choosing output directory.

LIST OF TABLES

• Table 1. Predictive relationships for |E*|
• Table 2. Model variables.
• Table 3. Example of summarized mixture and binder properties in the original Witczak database.
• Table 4. Summary of |G*| data available in the Witczak binder database.
• Table 5. Summary of |G*| data available in the FHWA mobile trailer database.
• Table 6. Summary of |G*| data available in the FHWA TPF-5(019) binder database.
• Table 7. Summary of |G*| data available in the NCDOT binder database.
• Table 8. Summary of |G*| data available in the Citgo binder database.
• Table 9. Summary of |G*| data available in the WRI database.
• Table 10. Summary of |E*| data available in the processed Witczak mixture database.
• Table 11. Summary of |E*| data available in the FHWA I mobile trailer mixture database.
• Table 12. Summary of |E*| data available in the FHWA II mobile trailer mixture database.
• Table 13. Summary of |E*| data available in the FHWA TPF-5(019) mixture database.
• Table 14. Summary of |E*| data available in the NCDOT mixture database.
• Table 15. Summary of |E*| data available in the WRI database.
• Table 16. Summary of |E*| data available in the Citgo mixture database.
• Table 17. Summary of |E*| data available in the M_R database.
• Table 18. Summary of extracted LTPP data.
• Table 19. Description of |G*|-based ANN models.
• Table 20. Description of viscosity-based ANN models.
• Table 21. Parameters and number of nodes used in developed ANN models.
• Table 22. Geometry coefficients.
• Table 23. Probability distribution of error functions of each ANN model.
• Table 24. Input ranges of different ANN models.
• Table 25. Limiting |E*| values used for QC #6.
• Table 26. Statistics of LTPP data populated with |E*|.
• Table 27. Structure and format of the TST_ESTAR_MASTER table.
• Table 28. Structure and format of the TST_ESTAR_MODULUS table.
• Table 29. Structure and format of the TST_ESTAR_MODULUS_COEFF table.
• Table 30. Structure and format of the TST_ESTAR_GSTAR_INPUT table.
• Table 31. Structure and format of the TST_ESTAR_GSTAR_CAM_COEFF table.
• Table 32. Structure and format of the TST_ESTAR_VOLUM_INPUT table.
• Table 33. Structure and format of the TST_ESTAR_VISC_INPUT table.
• Table 34. Structure and format of the TST_ESTAR_VISC_MODEL_COEFF table.
• Table 35. Structure and format of the TST_ESTAR_MR_INPUT table.
• Table 36. Relationship between asphalt binder grade and viscosity parameters.
• Table 37. Calibrated CAM model and t-T shift factor function coefficients using BBR data.
• Table 38. Calibrated CAM model and t-T shift factor function coefficients omitting BBR data.
• Table 39. Percentage of difference between BBR-calibrated and non-BBR-calibrated |G*| at TP-62 temperatures and frequencies.
• Table 40. Percentage of log difference between BBR-calibrated and non-BBR-calibrated |G*| at TP-62 temperatures and frequencies.
• Table 41. PAR model coefficient summary for Superpave™ high temperature grades.
• Table 42. PAR model verification dataset summary.
• Table 43. TP summary.
• Table 44. Test mixture volumetric properties.
• Table 45. Statistical summary of AMPT and TP-62 test results.
• Table 46. Percentage of difference between AMPT versus TP-62 database based on similar ranges of different variables.
• Table 47. Summary of database used for training ANN models.
• Table 48. Summary of the database used for verification of ANN models.
• Table 49. Description of the developed ANN Models and their validation statistics.
• Table 50. W_ik¹ matrix elements for M_R ANN (part 1).
• Table 51. W_ik¹ matrix elements for M_R ANN (part 2).
• Table 52. B_k¹ vector elements for M_R ANN (transposed for convenience).
• Table 53. W_kj² matrix elements for M_R ANN (part 1).
• Table 54. W_kj² matrix elements for M_R ANN (part 2).
• Table 55. W_kj² matrix elements for M_R ANN (part 3).
• Table 56. B_j² vector elements for M_R ANN (transposed for convenience).
• Table 57. W_jl³ vector elements for M_R ANN (part 1).
• Table 58. W_jl³ vector elements for M_R ANN (part 2).
• Table 59. W_jl³ vector elements for M_R ANN (part 3).
• Table 60. Normalization parameters for M_R ANN.
• Table 61. W_ik¹ matrix elements for VV ANN.
• Table 62. B_k¹ vector elements for VV ANN (transposed for convenience).
• Table 63. W_kj² matrix elements for VV ANN (part 1).
• Table 64. W_kj² matrix elements for VV ANN (part 2).
• Table 65. W_kj² matrix elements for VV ANN (part 3).
• Table 66. W_kj² matrix elements for VV ANN (part 4).
• Table 67. B_j² vector elements for VV ANN (transposed for convenience).
• Table 68. W_j³ vector elements for VV ANN.
• Table 69. Normalization parameters for VV ANN.
• Table 70. W_ik¹ matrix elements for GV ANN.
• Table 71. B_k¹ vector elements for GV ANN (transposed for convenience).
• Table 72. W_kj² matrix elements for GV ANN (part 1).
• Table 73. W_kj² matrix elements for GV ANN (part 2).
• Table 74. W_kj² matrix elements for GV ANN (part 3).
• Table 75. B_j² vector elements for GV ANN (transposed for convenience).
• Table 76. W_j³ vector elements for GV ANN.
• Table 77. Normalization parameters for GV ANN.
• Table 78. Relationship between binder purchase specification grade and A and VTS parameters.
• Table 79. File format for lab-aged files.
• Table 80. File format for field-aged files.
• Table 81. Output data format for single ANNACAP use.
• Table 82. Summary file format from batch mode in ANNACAP.
• Table 83. Output data format for batch mode ANNACAP use.

LIST OF ABBREVIATIONS AND SYMBOLS

Abbreviations

Symbols

|E*|	Dynamic modulus
|G*|	Dynamic shear modulus
MR	Resilient modulus
t-T	Time-temperature shift factors
ρ200	Percentage of aggregate passing #200 sieve
ρ4	Percentage of aggregate retained #4 sieve
ρ3/8	Percentage of aggregate retained 3/8-inch sieve
ρ¾	Percentage of aggregate retained ¾-inch sieve
Va	Percentage of air void
Vbeff	Percentage of effective asphalt content (by volume of mix)
f	Loading frequency
η	Binder viscosity
|G*|b	Dynamic shear modulus of asphalt binder
δb	Binder phase angle associated with |G*|b
fs	Dynamic shear frequency
T	Temperature
TR	Temperature in Rankine scale
|E*|m	Dynamic modulus of hot mix asphalt (pounds per square inch)
Pc	Aggregate contact volume
ø	Phase angle of hot mix asphalt
|G*|g	Dynamic shear modulus of asphalt binder at the glassy state
Vmix	Air voids by volume of the mix
ω	Angular frequency in radians per second
t	Time
fR	Reduced frequency
me	Fitting coefficient
k	Fitting coefficient
δ	Binder phase angle (degree)
Gmb	Bulk specific gravity
Gmm	Maximum specific gravity
SSE	Sum of squared error
Sy	Standard deviation
Se	Standard error
σa	Applied stress
εr	Recoverable strain
ν	Poisson's ratio
P	Applied load
U	Recoverable horizontal displacement
V	Recoverable horizontal displacement
k1	Constant value in NCHRP 1-28 elastic solution for Poisson's ratio
k2	Constant value in NCHRP 1-28 elastic solution for Poisson's ratio
k3	Constant value in NCHRP 1-28 elastic solution for Poisson's ratio
k4	Constant value in NCHRP 1-28 elastic solution for Poisson's ratio
E	Young's modulus
D	Compliance
R	Radius of specimen
χ	Horizontal distance from center of specimen
E'	Storage modulus
E"	Loss modulus
E∞	Equilibrium modulus
ωr	Angular reduced frequency
Ei	Modulus of the ith Maxwell element
ρi	Relaxation time of the ith Maxwell element
Akj	Matrix element in the kth row and jth column of matrix A
Bk	Vector element in the kth row of vector B
τj	Retardation time of the jth Voigt element determined a priori
tk	Time of interest
α1	Shift factor coefficient 1
α2	Shift factor coefficient 2
α3	Shift factor coefficient 3
(log|E*|ANN)i	Logarithm of the modulus determined from the ANN models at a particular temperature frequency combination
(log|E*|fit)i	Logarithm of the modulus determined from the optimized sigmoidal fit
(log|E*|avg)i	Logarithm of the average modulus determined from the ANN models for a given layer
A	Intercept of temperature susceptibility relationship
Tcritical	Temperature in Rankine at which the viscosity is exactly equal to 2.7 x 1012 cP (0.0027 x 1012 Pas)
PEN	Penetration number at given test temperature
ν	Kinematic viscosity (cSt)
ρ	Density (oz/in3 (g/cm3))
aT	Time-temperature shift factor
ωT	Frequency at the physical temperature
ωTR	Reduced frequency of ωT at the reference temperature
ωc	Fitting coefficient
C1	Fitting coefficient
C2	Fitting coefficient
C3	Fitting coefficient
S(t)	Beam stiffness
D0	Regression coefficient
D1	Regression coefficient
|D*|	Dynamic axial creep compliance
∂|G*|/∂T	Derivative |G*| with respect to time
E(t)	Uniaxial relaxation modulus
E'(ω)	Storage modulus
D(t)	Creep compliance
KT	Temperature factors
Kω	Frequency factors
β1	Second order polynomial coefficient
β2	Second order polynomial coefficient
β3	Second order polynomial coefficient
f(T)	Transfer function
	Value of the nodes at the first hidden layer
	Transferred value of the nodes at the first hidden layer
	Value of the nodes at the second hidden layer
	Transferred value of the nodes at the second hidden layer
	Value of output node l (MR ANN)
	Value of the output node (GV ANN and VV ANN)
	Transferred value of the output node l, normalized output (MR ANN)
	Transferred value of the output node, normalized output (GV ANN and VV ANN)
Pi	Input variables
	Weight factors for the first hidden layer
	Weight factors for the second hidden layer
	Bias factors for the first layer
	Bias factors for the second layer
	Bias factors for the outer layer (MR ANN)
B0	Bias factor for the outer layer (GV ANN and VV ANN)
(Sigl)max	Maximum value for sigmoidal coefficient l in the trained data (MR ANN)
(Sigl)min	Minimum value for sigmoidal coefficient l in the trained data (MR ANN)
log |E*|max	Maximum log |E*| of the trained data (GV ANN and VV ANN)
log |E*|min	Minimum log |E*| of the trained data (GV ANN and VV ANN)
	Normalized value for given input variable, i
MINi	Minimum value of variable, i, in calibration dataset
MAXi	Maximum value of variable, i, in calibration dataset
Sig1	First sigmoidal function coefficient
Sig2	Second sigmoidal function coefficient
Sig3	Third sigmoidal function coefficient
Sig4	Fourth sigmoidal function coefficient
	Resilient modulus at 41° F (5 °C), MPa
	Resilient modulus at 77° F (25 °C), MPa
	Resilient modulus at 104° F (40 °C), MPa
R	Coefficient in WLF function
Ea	Coefficient in WLF function
tR	Inverse of reduced frequency of loading (Hz)
δ	Sigmoidal function fitting coefficient
β	Sigmoidal function fitting coefficient
D'	First vector component of |D*|
D"	Second vector component of |D*|
Vbe	The effective volume of the binder

EXECUTIVE SUMMARY

The dynamic modulus, |E*|, is a fundamental property that defines the stiffness characteristics of hot mix asphalt (HMA) mixtures as a function of loading rate and temperature. Given the significance of |E*| in pavement engineering, this project was undertaken to provide the Long-Term Pavement Performance (LTPP) database with |E*| estimates using material properties currently available for LTPP test sections. In this report, existing models used to estimate |E*| values and additional models that have been developed based on the use of artificial neural networks (ANNs) were evaluated. Using the results of the model evaluation, the research team developed a model selection hierarchy and populated the LTPP database with |E*| estimates at five temperatures and six frequencies. It also developed shift factors and sigmodial functions that can be used to construct mastercurves.

The seven models identified at the outset of this project as potentially suitable for the task at hand include the following:

1. Original Witczak equation (National Cooperative Highway Research Program (NCHRP) 1-37A).⁽²⁾
2. Modified Witczack dynamic shear (|G*|) equation (NCHRP 1-40D).⁽⁵⁾
3. Hirsch model.⁽⁶⁾
4. Law of mixtures parallel model.⁽⁷⁾
5. Resilient modulus (M_R)-based ANN model.
6. Viscosity-based ANN model.
7. Binding shear modulus (|G*|)-based ANN model.

The existing predictive models (1–4 above) are collectively referred to in this report as “closed-form models.” Specific comparisons are drawn regarding their forms and required input parameters.

An extensive independent database was required to develop the ANN models and to fairly assess the predictive capabilities of each model in the list of possible models. At the outset of the project, the most comprehensive material database available was compiled through the efforts of Dr. Matthew Witczak at Arizona State University. Witczak's database consists of 7,400 data points from 346 mixtures, all of which were used in the calibration of the NCHRP 1-40D predictive models.⁽⁵⁾ A smaller subset of the data (2,750 data points from 205 mixtures) was also used in developing the NCHRP 1-37A predictive model.⁽²⁾ In addition, the database contains |G*| data obtained from different materials and aging conditions. Through this research project, the Witczak database was combined with mixtures from other national projects and efforts undertaken at North Carolina State University (NCSU). The expanded mixture database currently includes 22,505 data points.

In addition to a mixture database, binder properties were compiled into a similarly expansive database. Substantial efforts have been expended to develop the appropriate binder data processing techniques. The required processing varied depending on the type of data available (i.e., |G*|, viscosity, or binder grade). Only the critical points are presented in this report, and the details are provided in the appendices.

Closed-form models were compared using datasets that were not used in the calibration of the respective models. It was found that the law of mixtures parallel model shows a significant bias, but the Hirsch model shows reasonable predictions, except for insensitivity under extreme conditions.^(7,6) For the verification database, the Hirsch model shows slightly better statistical predictions than either of the Witczak models.⁽⁶⁾ This finding, along with other statistical analyses, led the research team to adopt the Hirsch model input parameters into the viscosity-based (VV) and |G*|-based ANN models.

Comparisons between the ANN models and the closed-form models were made. Overall, the ANN models provide better predictability than any of the closed-form solutions. Additionally, the ANN models are more sensitive to the input parameters. Based on these findings, the ANN models were chosen to populate the LTPP database moduli values. The primary advantage of using ANN modeling over statistical regression techniques is that the functional form of the relationship is not needed a priori. Considering that many variables affect |E*| values and their interactions, the ANN technique may capture complicated nonlinear relationships between |E*| and other mixture variables better than regression analysis.

Early in the project, concerns arose because the database combined moduli that had been measured using two different methods, the American Association of State Highway and Transportation Officials (AASHTO) test protocol (TP)-62 and the asphalt mixture performance tester (AMPT) protocol.^(8,9,4) A study of the available databases revealed that the mixtures that are tested according to the AASHTO TP-62 protocol tend to yield higher moduli values than similar mixtures tested using the AMPT protocol. Statistical analysis to assess the significance of the difference was not performed, but the two data ranges tend to overlap, suggesting a lack of statistical significance in their differences. A limited experimental study wherein the modulus of a single mixture was measured using the two protocols is also discussed. The study shows a statistically significant difference of about 12 percent in the measured moduli across all studied temperatures and frequencies. However, in light of the fact that both protocols are readily available and that neither of the available protocols can be discounted without a more comprehensive and controlled experimental program, the decision was made to include all available data from both the AMPT protocol and AASHTO TP-62 in the calibration process.

Details of the three ANN models, including the required input parameters, model structure, and input range, are presented in this report. The models are prioritized based on engineering judgment and statistical analysis. From this prioritization, a decision tree was developed for populating |E*| of the LTPP layers (see figure 1). A user may follow this decision structure and determine the best model to use for the available input parameters.

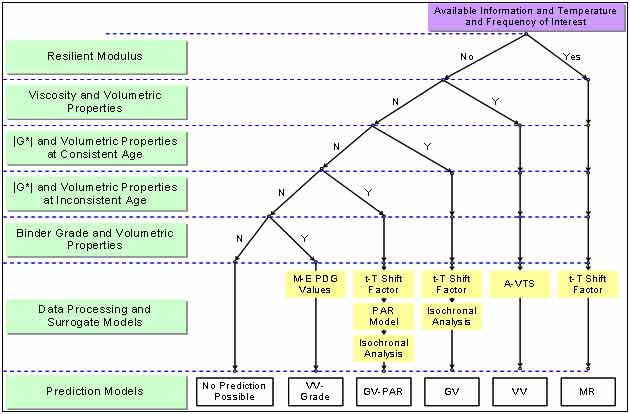
Figure 1. Illustration. Modulus prediction model decision tree.

At the end of phase I of this study, it was discovered that some State agencies report effective binder content by mass instead of by volume (i.e., gravimetric instead of volumetric). As a result, there were concerns about the use of a predictive model based on the volumetric properties of the asphalt mixtures. After reviewing the database and carrying out some volumetric computations, volumetric-based properties could still be calculated when gravimetric quantities were reported. Details of how these volumetric-based quantities were computed are provided in this report.

A key component to the prediction of moduli values is ensuring that the predicted values are rational and acceptable. To meet this criterion for the finalized ANN predictions, a set of quality control (QC) checks on both the input parameters and model predictions were performed. In total, seven QC checks were developed, one for the inputs and six for the modulus predictions, and are described in detail in section 6.2 of this report. Executable software, Artificial Neural Networks for Asphalt Concrete Dynamic Modulus Prediction (ANNACAP), was developed as part of this project for this purpose. The software can be run for individual layers (manual mode) or all layers simultaneously (batch mode). An unpublished manual for the software is provided in appendix E of this report.

Statistics for the population effort are also presented in this report. The LTPP database contains information for 1,806 layers that meet the criteria established for this project. These layers have binder data available at a combination of different aging conditions, including unaged or original-aged, rolling thin film oven (RTFO)-aged, pressure-aging vessel (PAV)-aged, and field-aged. For the field-aged data, 2,223 records are available because some layer properties have been measured at different dates. The total resulting number of records is 7,641. Using the combined ANN models and requisite internal QC checks, modulus values are predicted for 363 records/layers in the original-aged level, 469 records/layers in the RTFO-aged level, 1 record/layer in the PAV-aged level, and 503 records in the field-aged level. Combined, these numbers translate to predictions for 17.5 percent of the total number of records available. However, these records are distributed in such a way that a higher percentage of the layers has some sort of valid prediction. Of the 1,806 layers in the database, 1,010 layers, or 56 percent, have a modulus prediction for some aging condition. Of these 1,010 layers, 615 layers, or 34 percent of the total 1,806 layers, have reasonable predictions (i.e., an “A” grade), and 89 layers, or 4.9 percent of the total 1,806 layers, have unreasonable predictions (i.e., an “F” grade). The remaining 306 layers, representing 17 percent of the 1,806 layers, have questionable predictions (i.e., a “C” grade). Thus, the total percentage of layers with a completely valid or questionable prediction is 51 percent. The quality grading system referenced is different from the standard record status definition used in the LTPP database.⁽¹⁰⁾ The research team established strict QC checks to ensure that only the highest quality data were assigned an “A” grade. The data that did not achieve an “A” grade were not considered unusable data. All predictions are included in the database so that users can determine the data that are suitable for their needs. In addition, the Federal Highway Administration (FHWA) can revise the criteria used for the quality checks as deemed appropriate based on the opinions of its experts.