U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

 
REPORT
This report is an archived publication and may contain dated technical, contact, and link information
Back to Publication List        
Publication Number:  FHWA-HRT-10-066    Date:  October 2011
Publication Number: FHWA-HRT-10-066
Date: October 2011

 

Impact of Design Features on Pavement Response and Performance in Rehabilitated Flexible and Rigid Pavements

Chapter 7. Analysis of Rehabilitated Pavement Structures Using MEPDG

Introduction

One part of this study was to evaluate rehabilitated pavement structures using MEPDG.(1) The objective of the task was to compare MEPDG-predicted performance with field-measured data and verify the current calibration against predictions of rehabilitated pavement structures. Flexible pavement sections from the SPS-5 experiment and rigid/composite pavement sections from the SPS-6 experiment were subject to MEPDG analysis, and the results were compared to actual distress measurements from LTPP surveys. All JPCP sections from both experiments were used in this analysis.

This research also produced a database of rehabilitated sections extracted from the LTPP program that can be used to perform local calibrations. The database is described in appendix E.

MEPDG Overview

MEPDG is based on principles of both engineering mechanics and field verification to estimate performance.(1) A mechanistic approach is used to predict pavement responses to traffic loads, and pavement performance is then estimated based on empirical relationships developed from evidence from field data.

Data Requirements

MEPDG considers three main factors in the analysis of pavement performance: traffic, environment, and pavement structure.(1) Each of these factors is described below.

Traffic

Traditionally, traffic inputs for pavement design have been single numbers, such as the annual average daily traffic or ESAL concepts. In developing MEPDG, it was recognized that these parameters do not sufficiently characterize the variable effects of axle loads distributions, traffic characteristics (speed, wander, etc.), and axle and tire configuration on pavements.

MEPDG utilizes the traffic spectra, and the anticipated or historical traffic is classified according to axle type (single, tandem, tridem, quad, or special axles) and the distribution of axle weights within each axle type.

Environment

There are three basic elements required to consider the environmental factors in MEPDG analysis: (1) site-specific environmental data, (2) material-specific data on thermal-related properties, and (3) an algorithm to compute the transmission of heat and moisture within the pavement structure. MEPDG considers the seasonal effects of temperature and moisture on material properties of pavement layers, and consequently, on pavement response and performance.

Pavement Structure

As with any pavement analysis and design procedure, it is necessary to define the materials used in the structure including their properties, thicknesses, and construction characteristics. MEPDG can be used to analyze both new and rehabilitated PCC, HMA, and composite (PCC and HMA) pavements. Measured mechanical properties can be used to characterize the material's behavior to loading and thermal variations.

Summary of Data Required for MEPDG Analysis

Table 91 provides a list of the data required for MEPDG analysis. The current national calibration is defined as level 3 input for material properties. To provide an equivalent level of comparison, the input data for this study were collected as level 3.

Table 91. Predominant source of data used for preliminary statistical analysis and MEPDG performance models

Input Group

Input Parameter

Data Source

Truck traffic

Axle load distributions (single, tandem, and tridem)

LTPP

Truck volume distribution

LTPP

Lane and directional truck distributions

LTPP

Tire pressure

MEPDG defaults

Axle configuration and tire spacing

MEPDG defaults

Truck wander

MEPDG defaults

Climate

Temperature, wind speed, cloud cover, precipitation, and relative humidity

National Climate Data Center

Material properties

Unbound layers and subgrade

Resilient sodulus-subgrade

all unbound layers

MEPDG defaults

Resilient modulus-base/subbase

MEPDG defaults

Classification and volumetric properties

LTPP

Moisture-density relationships

LTPP

Soil-water characteristic relationships

MEPDG defaults

Saturated hydraulic conductivity

MEPDG defaults

HMA

HMA dynamic modulus

LTPP

HMA creep compliance and indirect tensile strength

MEPDG defaults

Volumetric properties

LTPP

HMA coefficient of thermal expansion

MEPDG defaults

PCC

PCC elastic modulus

LTPP

PCC flexural strength

LTPP

PCC coefficient of thermal expansion

LTPP

All materials

Unit weight

LTPP

Poisson's ratio

MEPDG defaults

Other thermal properties, conductivity, heat capacity, and surface absorptivity

MEPDG defaults

Note: MEPDG generates climate files using data from the National Climate Data Center.

Latest Calibration Efforts

The original calibration for MEPDG was finalized in 2004 and was based on performance data from several projects, mainly from the LTPP program for data collected until 2001. Recently, an effort under NCHRP Projects 1-40A and 1-40D added 4–5 years of new data to improve the national calibration.(21,22) A summary of the efforts carried out to obtain current calibration by pavement type is provided below.

Flexible Pavement Calibration

Data from 49 sections from the GPS-6B and SPS-5 projects were used for the calibration and validation of HMA overlays over existing AC structures. Data from three sections of the SPS-6 experiment were used for the calibration and validation of the HMA overlay over existing fractured slab structures. Data from seven sections from the GPS-7B and SPS-6 projects were used for the calibration and validation of HMA overlay over existing JPCP structures.

PCC Rehabilitation Calibration

Calibration data were obtained from the LTPP database, the American Concrete Pavement Association Longevity and Performance of Diamond-Ground Pavements study, and NCHRP Project 10-41, Guidelines for the Design of Unbonded PCC Overlays.(23) Different datasets were used to calibrate restored JPCP.

Data were obtained from the SPS-6 experiment, specifically sections 0601, 0602, and 0605, which corresponded to JPCP sections without overlay in the rehabilitation strategy. The restoration performed on these test sections ranged from the no treatment control section to full depth patching and retrofitting joints with dowels. Specific restoration treatments included the following:

Rehabilitated Flexible Pavements

The performance of the 500-ft (152.5-m) sections in the SPS-5 experiment was estimated using MEPDG software Version 1.003. Load-associated distress trends were compared to LTPP-measured distress values from surveys. Three pavement distress types were evaluated including roughness, rutting, and

It should be noted that LTPP-measured distress data and MEPDG-predicted performance data do not have the same units of measurement. As a result, MEPDG-predicted performance was converted to match the units used in the LTPP database. Table 92 explains the conversion used in this analysis.

Table 92. Conversion of MEPDG-predicted performance data to LTPP units.

Performance Parameter

LTPP Units for the Parameter

MEPDG Units for the Parameter

Conversion to LTPP Units

Fatigue cracking

ft2

Percentage of the design lane cracked

 (Percentage cracked) x 500_ft×12_ft/100

Longitudinal cracking

ft

ft/mi

 (Distress in ft/mile) x 500_ft/5280_ft

Transverse cracking

ft

ft/mi

 (Distress in ft/mile) x 500_ft/5280_ft

1 ft = 0.305 m
1 ft2 = 0.093 m2
1 mi = 1.61 km
Note: The underscores indicate the format used when entering data into the LTPP database.

Both the LTPP-measured data and the MEPDG-predicted distresses were converted into SI units for plotting. The comparative analyses are presented in the following sections.

Roughness

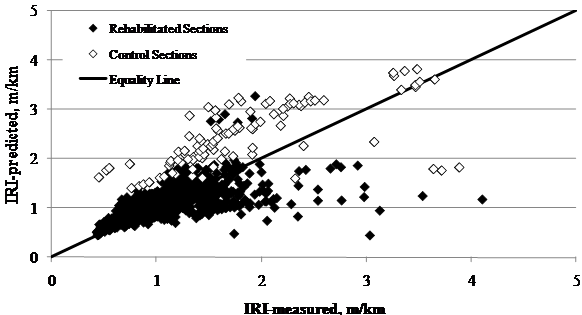
Predicted versus measured pavement roughness was evaluated in terms of IRI values. Figure 67 describes predicted versus measured performance for all sections in the SPS-5 experiment. The data were grouped by rehabilitated and control sections (without overlay), and the  results were reasonable overall. However, some bias was noted for both sets of data. The results for rehabilitated sections showed a bias for underprediction of IRI, whereas the control sections showed a tendency for bias of overprediction. Because the analysis of the control sections considered the pavement life since its construction and the window monitored for rehabilitated pavements were defined for several years after the initial construction, MEPDG was overpredicting the IRI levels for new flexible pavements during the last portion of the pavement's life.

The MEPDG out-of-the-box models were calibrated using only new pavement sections. This exercise involving rehabilitated sections from the SPS-5 experiment indicated that the roughness model could be used to predict IRI values with fairly good accuracy in rehabilitated sections. Local calibration of the current model may further improve accuracy of roughness predictions in rehabilitated sections.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for all Specific Pavement Study (SPS)-5 sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by white diamond markers for control sections and black colored diamond markers for rehabilitated sections. The points are spread evenly around the solid line with a majority of measured and predicted IRI values ranging from 2.64 to 10.56 ft/mi (0.5 to 2.0 m/km). There is a high concentration of data points corresponding to rehabilitated sections near the line of equality, while the data points for control sections are mostly above the equality line with measured and predicted IRI values ranging from 2.64 to 15.84 ft/mi (0.5 to 3 m/km). The results for rehabilitated sections show a bias for underprediction of IRI, whereas the control sections show a tendency for bias of overprediction.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 67. Graph. LTPP-measured versus MEPDG-predicted IRI for all SPS-5 sections.

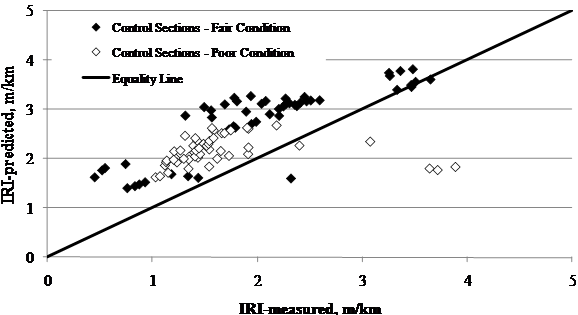
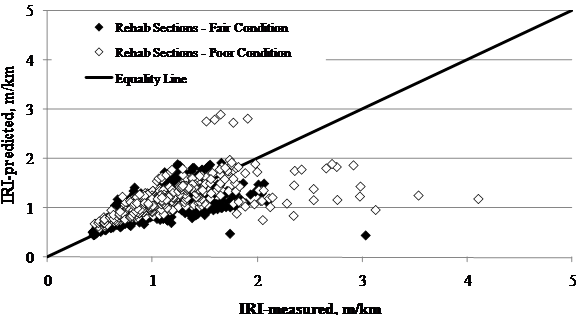
The level of accuracy for the MEPDG roughness model predictions was similar for the control sections with poor and fair pavement conditions prior to the beginning of the experiment (see figure 68). Similar results were found for rehabilitated sections (see figure 69). The difference in this case was that there was a tendency to underpredict rehabilitated sections with poor overall condition and IRI values above 10.56 ft/mi (2 m/km).

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-5 control sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by white diamond markers for control sections in fair condition and black colored diamond markers for control sections in poor condition. The data points for both cases are mostly above the line of equality, with a majority of measured and predicted IRI values ranging from 5.28 to 15.84 ft/mi (1 to 3 m/km). The level of accuracy for the MEPDG roughness model predictions is similar for the control sections with poor and fair pavement condition prior to the beginning of the experiment.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 68. Graph. LTPP-measured versus MEPDG-predicted

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-5 rehabilitated sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by white diamond markers for rehab sections in fair condition and black colored diamond markers for rehabilitated sections in poor condition. The data points for both cases are mostly above the line of equality, with a majority of measured and predicted IRI values ranging from 5.28 to 15.84 ft/mi (1 to 3 m/km). The level of accuracy for the MEPDG roughness model predictions is similar for the rehabilitated sections with poor and fair pavement condition prior to the beginning of the experiment.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 69. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-5 rehabilitated sections.

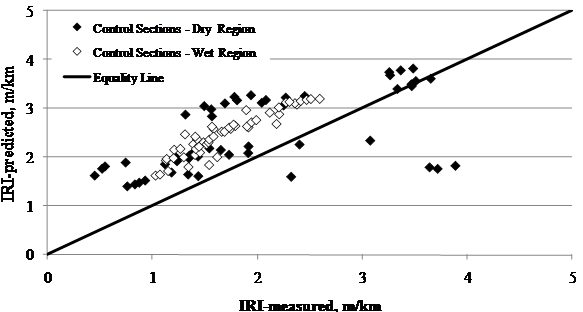
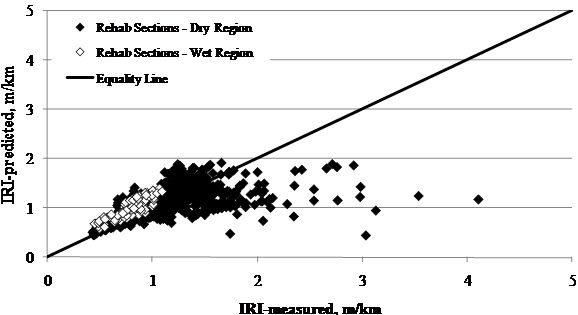
Another site factor with a visible impact on the accuracy of the models was the climate condition. Results in figure 70 and figure 71 suggest that despite the small bias for the control sections, the current model did a better job predicting IRI in sections located in wet regions in comparison to dry locations, especially for rehabilitated sections. The other climate variable in the SPS-5 experiment was temperature (freeze versus no-freeze); however, temperature did not influence the accuracy of predictions.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-5 control sections in wet and dry regions. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by white diamond markers for control sections in dry regions and black colored diamond markers for control sections in wet regions. The data points for both cases are mostly above the line of equality, with a majority of measured and predicted IRI values ranging from 5.28 to 15.84 ft/mi (1 to 3 m/km).

1 ft = 0.305 m
1 mi = 1.61 km

Figure 70. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-5 control sections in wet and dry regions.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-5 rehabilitated sections in wet and dry regions. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by white diamond markers for rehab sections in dry regions and black colored diamond markers for rehab sections in wet regions. The data points for both cases are mostly clustered around the line of equality, with the majority of measured and predicted IRI values ranging from 2.64 to 5.28 ft/mi (0.5 to 1 m/km) for rehab sections in wet regions and 2.64 to 21.12 ft/mi (0.5 to 4 m/km) for rehab sections in dry regions. The figure suggests that the current model better predicts IRI in sections located in wet regions than it does in dry locations.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 71. Graph. LTPP-measured versus MEPDG-predicted

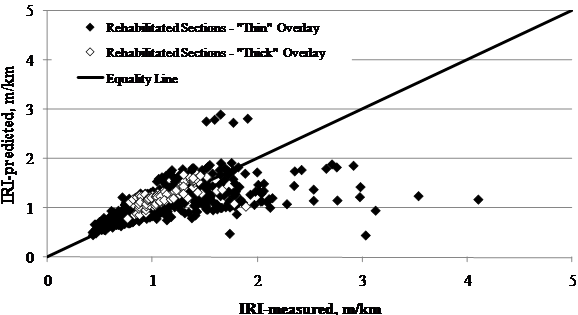
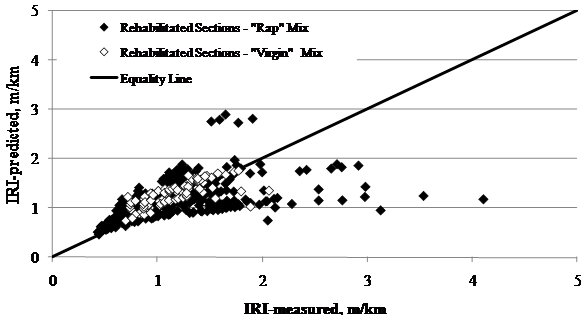
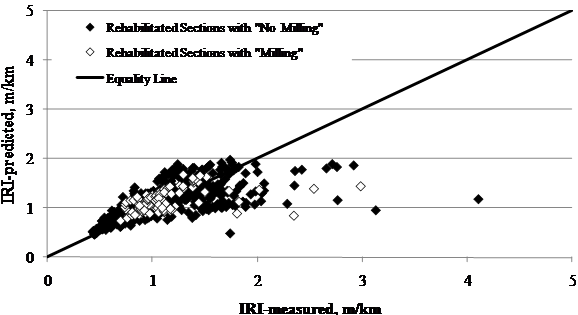
The influence of design features on the MEPDG performance predictions was also investigated. The results obtained for the rehabilitated sections were grouped by overlay thickness, mix type, and milling. The results of predicted versus measured IRI performance are shown in figure 72 through figure 74.

The following observations were made:

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-5 rehabilitated sections grouped by overlay thickness. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by white diamond markers for rehabilitated sections with thin overlay and black colored diamond markers for rehabilitated sections with thick overlay. The data points for both cases are mostly closely clustered to the line of equality, with the majority of measured and predicted IRI values ranging from 2.64 to 10.56 ft/mi (0.5 to 2 m/km).

1 ft = 0.305 m
1 mi = 1.61 km

Figure 72. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-5 rehabilitated sections grouped by thickness.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-5 rehabilitated sections based on mix type. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by white diamond markers for rehabilitated sections with thin overlay and black colored diamond markers for rehabilitated sections with thick overlay. The data points for both cases are mostly closely clustered to the line of equality, with the majority of measured and predicted IRI values ranging from 2.64 to 10.56 ft/mi (0.5 to 2 m/km).

1 ft = 0.305 m
1 mi = 1.61 km

Figure 73. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-5 rehabilitated sections grouped by mix type.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted international Roughness Index (IRI) for Specific Pavement Study (SPS)-5 rehabilitated sections based on milling work. This plot has a solid diagonal line of equality going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by white diamond markers for rehabilitated sections with thin overlay and black colored diamond markers for rehabilitated sections with thick overlay. The data points for both cases are mostly closely clustered to the line of equality, with the majority of measured and predicted IRI values ranging from 2.64 to 10.56 ft/mi (0.5 to 2 m/km).

1 ft = 0.305 m
1 mi = 1.61 km

Figure 74. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-5 rehabilitated sections grouped by milling.

It is important to note that the group of points with high IRI levels in figure 72 through
figure 74 (IRI > 9.50 ft/mi (1.8 m/km)) were sections classified as having poor initial conditions. Results demonstrate that these sections did not perform well and that, in general, MEPDG underpredicted the IRI levels for these sections. Overall, the current MEPDG IRI model predicts performance reasonably well, provided it is calibrated using data from new pavement sections. Local calibration of the model is likely to improve accuracy and reduce bias, especially for rehabilitated sections that were in poor condition prior to rehabilitation.

Rutting

When comparing actual rutting versus MEPDG-estimated rutting, control sections and rehabilitated sections were evaluated. The goal was to observe the trends when analyzing new pavements and rehabilitated pavements. Control section estimates were obtained by running the MEPDG software for a new section; however, the data screened for the analysis were those gathered during the survey period of the SPS-5 sites.

For most control sections, MEPDG overpredicted rutting, while for rehabilitated sections, there was not an evident bias (see figure 75). Nonetheless, in many cases, the rutting levels were either underpredicted or overpredicted. The control sections were treated as new sections; therefore, the rutting predictions included base and subgarde rutting. For overlays, the only rutting considered in MEPDG was that of the overlay, and no rutting was allowed in the underlying layers. Attempts were made to identify whether there was a consistent reason for underpredictions or overpredictions of rutting (i.e., site conditions or design features of the rehabilitated sections), but no reason was found. The results in figure 75 suggest that the rutting model needs further calibration to reduce bias in predicting the performance of new pavements. Most likely, the lack of sufficient rutting data for each pavement layer during the initial MEPDG calibration and the need to assume individual layer contribution to total rutting led to the results in the figure. A revised model is recommended to improve accuracy in predicting the performance of rehabilitated pavements.

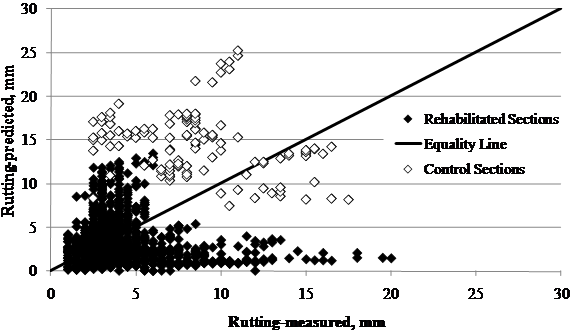
This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted rutting for Specific Pavement Study (SPS)-5 sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured rutting in millimeters, and the y-axis shows the predicted rutting in millimeters. The individual points are represented by white diamond markers for control sections and black colored diamond markers for rehabilitated sections. The MEPDG-predicted values for control sections are in two clusters. The first cluster is above the line of equality and has a predicted rutting of 0.39 to 0.975 inches (10 to 25 mm) corresponding to a measured rutting of 0 to 0.39 inches (0 to 10 mm). Rehabilitated sections have low values of measured rutting, with a majority of points below the line of equality. There is a high concentration of points in the range of 0 to 0.29 inches (0 to 7.5 mm) for rutting.

1 inch = 25.4 mm

Figure 75. Graph. LTPP measured versus MEPDG predicted rutting for SPS-5 sections.

Cracking

MEPDG estimates of top-down longitudinal cracking, low temperature transverse cracking,
and bottom-up alligator fatigue cracking were computed and compared to actual survey measurements available in the LTPP database for the SPS-5 experiment. Predicted versus measured longitudinal cracking results are shown in figure 76. With the exception of one site, all predictions had zero or near-zero values. MEPDG consistently underpredicts longitudinal cracking for both new and rehabilitated pavements. When comparing transverse cracking, MEPDG does not predict any transverse cracking in any of the analyses that were performed.

Fatigue cracking was computed as the sum of alligator cracking (developed in the new overlay HMA layer) and reflective cracking (cracking in the old surface propagated upward into the new layer). In MEPDG, these cracking patterns are represented by cracking types FC1 and FC2, respectively. MEPDG predicts fatigue cracking on the surface as a "percentage of the design lane cracked."(1) The MEPDG fatigue cracking outputs were converted into cracked area according to table 92. Predicted fatigue cracking data were plotted against measured data and are presented in figure 77. It can be concluded from the comparative graph that the fatigue cracking model in MEPDG underpredicts the performance of both new and rehabilitated pavements.

The reflective cracking model dominates the total fatigue cracking predictions. If only the fatigue cracking associated with the new overlay layer is plotted against the measured fatigue cracking in the LTPP database, the MEPDG-predicted fatigue cracking is underpredicted (see figure 78). The figure suggests that reflective cracking propagating from the existing layer is the major contributor to the total fatigue cracking predictions. The reflective cracking model needs further improvements to reduce the bias and enhance its accuracy.

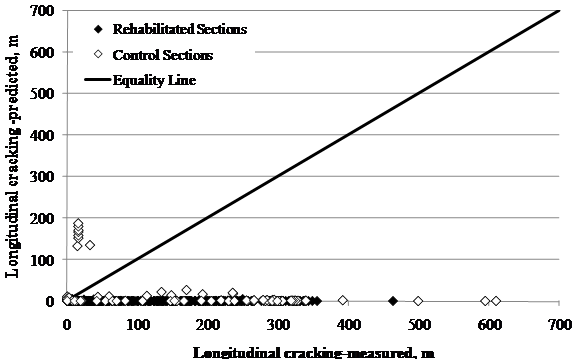
This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted longitudinal cracking for Specific Pavement Study (SPS)-5 sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured longitudinal cracking in meters, and the y-axis shows the predicted longitudinal cracking in meters. The individual points are represented by white diamond markers for control sections and black colored diamond markers for rehabilitated sections. The MEPDG-predicted values for control sections are in two clusters. The first cluster is above the line of equality and has a predicted longitudinal cracking of 328 to 656 ft (100 to 200 m) corresponding to a measured longitudinal cracking of about 32.8 ft (10 m). The second cluster contains the majority of data points, is below the line of equality, and has predicted longitudinal cracking values close to 0 ft (0 m). Measured rutting for rehabilitated sections is close to 0 ft (0 m), with measured longitudinal cracking values ranging from 0 to 1,558 ft (0 to 475 m).

1 ft = 0.305 m

Figure 76. Graph. LTPP-measured versus MEPDG-predicted longitudinal cracking for SPS-5 sections.

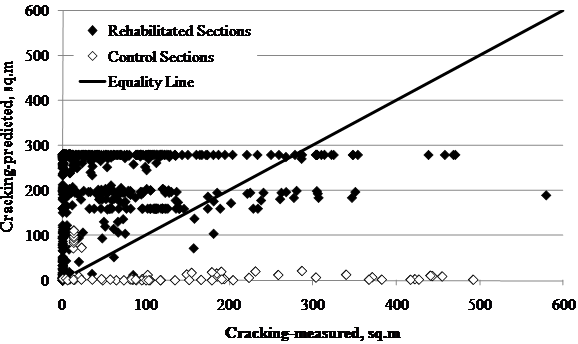
This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted cracking for Specific Pavement Study (SPS)-5 sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured cracking in square meters, and the y-axis shows the predicted cracking in square meters. The individual points are represented by white diamond markers for control sections and black colored diamond markers for rehabilitated sections. The MEPDG-predicted values for control sections are in two clusters. The first cluster is above the line of equality and has a predicted rutting of 807.3 to 1,184.04 ft2 (75 to 110 m2) corresponding to a measured rutting of about 0.39 inches (10 mm). Rehabilitated sections are mostly above the line of equality with a high concentration of points on the y-axis ranging from 0 to 3,121.56 ft2 (0 to 290 m2) and parallel to the x-axis at predicted values of 3,121.56 and 2,152.8 ft2 (290 and 200 m2), with measured cracking values ranging from 0 to 3,229.2 ft2 (0 to 300 m2).

1 ft2 = 0.093 m2

Figure 77. Graph. LTPP-measured versus MEPDG-predicted fatigue and reflective cracking for SPS-5 sections.

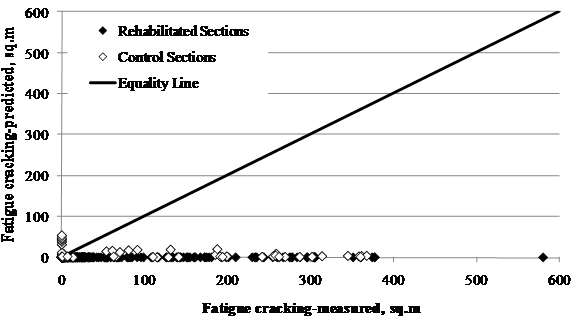
This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted fatigue cracking for Specific Pavement Study (SPS)-5 sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured fatigue cracking in square meters, and the y-axis shows the predicted fatigue cracking in square meters. The individual points are represented by white diamond markers for control sections and black colored diamond markers for rehabilitated sections. The MEPDG-predicted values for control sections are in two clusters. The first cluster is on the y-axis above the line of equality and has a predicted fatigue cracking of 322.9 to 645.8 ft2 (30 to 60 m2). The second cluster that contains the majority of data points is below the line of equality and has predicted fatigue cracking values close to 0 ft2 (0 m2). Measured rutting for rehabilitated sections is close to zero, with measured fatigue cracking values ranging from 0 to 1,935.2 ft (0 to 590 m).

1 ft2 = 0.093 m2

Figure 78. Graph. LTPP-measured versus MEPDG-predicted fatigue cracking for SPS-5 sections.

Rehabilitated Rigid Pavements

The performance of the 500-ft (152.5-m) sections in the SPS-6 experiment was estimated using MEPDG software Version 1.003. Estimated and actual load-associated distress trends were compared for the following

Both the LTPP-measured data and the MEPDG-predicted data were converted into SI units for plotting. The comparative analyses are presented in the following sections.

Roughness

Pavement roughness was evaluated in terms of IRI values. Figure 79 and figure 80 describe predicted versus measured roughness for all sections in the SPS-6 experiment. Figure 79 presents results for all the sections in which the rehabilitation treatment had no overlay. These sections,  0601, 0602, and 0605, received only restoration treatments in the PCC layer or no treatment at all. Figure 80 shows the trends for all sections in which the rehabilitation treatment had overlay
(sections 0603, 0604, 0606, 0607, and 0608). Both figures suggest that the IRI model provides fairly good predictions of roughness performance. Sections without overlays were slightly underpredicted, especially for sections with restoration (minimum or maximum). Sections with overlays were predicted more consistently with measured values, especially for IRI values lower than 9.50 ft/mi (1.8 m/km). For IRI values higher than 1.8 m/km, the models consistently underpredicted performance.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-6 sections with overlay. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by black colored triangular markers for maximum restoration, crosses for minimum restoration, and circles for control sections. The data points are widespread with IRI values ranging from 4.2 to 20.1 ft/mi (0.8 to 3.8 m/km). There is also a high concentration of data points near the line of equality, at measured and predicted IRI values of about 3.96 to 9.24 ft/mi (0.75 to 1.75 m/km). Data points for "Maximum Restoration" are mostly below the line of equality, while the rest are both above and below the line of equality.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 79. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-6 sections without overlay.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-6 sections without overlay. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by diamonds for crack/break and seal, triangular markers for maximum restoration, crosses for minimum restoration, and circles for saw and seal. The data points are widespread, with IRI values ranging from 4.2 to 20.1 ft/mi (0.8 to 3.8 m/km). There is also a high concentration of data points near the line of equality, at measured and predicted IRI values of about 3.96 to 9.24 ft/mi (0.75 to 1.75 m/km). Data points for maximum restoration, minimum restoration, and saw and seal are close to the line of equality, while several data points for crack/break and seal are below the line of equality.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 80. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-6 sections with overlay.

Climate condition influenced MEPDG roughness predictions. Figure 81 and figure 82 present predicted versus measured IRI for sites located in wet and dry regions. The results suggest that sites located in wet regions had predictions that were more accurate and less biased than sites located in dry regions; however, there was still underprediction for high IRI levels. MEPDG consistently underpredicts high IRI values (higher than  9.50 ft/mi (1.8 m/km)) in dry regions. Figure 83 and figure 84 show predicted versus measured IRI for sites located in freeze and
no-freeze regions. The results suggest that sites located in no-freeze regions have predictions that are more accurate and less biased than sites located in freeze regions. MEPDG consistently underpredicts high IRI values (higher than 9.50 ft/mi (1.8 m/km)) in freeze regions.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-6 sections in wet regions. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by black colored diamond markers for sections in wet regions with no overlay and white diamond markers for sections in wet regions with a 4- or 8-inch (102- or 203-mm) overlay. The data points are widespread with IRI values ranging from 4.2 to 20.1 ft/mi (0.8 to 3.8 m/km). There is also a high concentration of data points near the line of equality at measured and predicted IRI values of about 3.96 to 9.24 ft/mi (0.75 to 1.75 m/km). Data points for "Wet No Overlay" are mostly below the line of equality while the "Wet 4-inch or 8-inch" (102- or 203-mm) overlay points are on or above the line of equality.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 81. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-6 sections in wet regions.

This scatter plot shows long-term pavement performance (LTPP) measured versus Mechanistic Empirical Pavement Design Guide (MEPDG) predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-6 sections in dry regions. This plot has a solid diagonal line of equality going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by black colored diamond markers for sections in dry regions with no overlay and white diamond markers for sections in dry regions with a 4- or 8-inch (102- or 203-mm) overlay. While measured IRI values range from 5.28 to 21.12 ft/mi (1.0 to 4.0 m/km), predicted IRI values are mostly in the 5.28- to 10.56-ft/mi (1.0- to 2.0-m/km) range with a high concentration of data points near the line of equality, with measured and predicted values of 5.28 to 7.92 ft/mi (1 to 1.5 m/km). Most of the data points are on or below the line of equality.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 82. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-6 sections in dry regions.

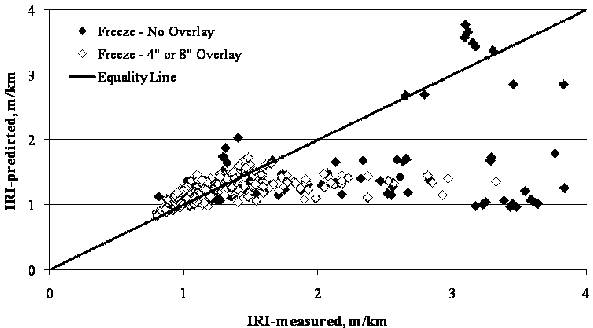
This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-6 sections in freeze regions. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by black colored diamond markers for sections in freeze regions with no overlay and white diamond markers for sections in freeze regions with a 4- or 8-inch (102- or 203-mm) overlay. While measured IRI values range from 5.28 to 21.12 ft/mi (1.0 to 4.0 m/km), predicted IRI values are mostly in the 5.28- to 10.56-ft/mi (1.0- to 2.0-m/km) range with a high concentration of data points near the line of equality, with measured and predicted values of 5.28 to 7.92 ft/mi (1 to 1.5 m/km).

1 ft = 0.305 m
1 mi = 1.61 km

Figure 83. Graph. LTPP-measured versus MEPDG-predicted IRI for SPS-6 sections in freeze regions.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted International Roughness Index (IRI) for Specific Pavement Study (SPS)-6 sections in no-freeze regions. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured IRI in meters per kilometer, and the y-axis shows the predicted IRI in meters per kilometer. The individual points are represented by black colored diamond markers for sections in no-freeze regions with no overlay and white diamond markers for sections in no-freeze regions with a 4- or 8-inch (102- or 203-mm) overlay. While measured IRI values range from 5.28 to 21.12 ft/mi (1.0 to 4.0 m/km), predicted IRI values are mostly in the 5.28- to 15.84-ft/mi (1.0- to 3.0-m/km) range with a high concentration of data points near the line of equality, at measured and predicted values of about 5.28 to 7.92 ft/mi (1 to 1.5 m/km). Data points for "No Freeze No Overlay" are mostly below the line of equality, while the "No Freeze 4- or 8-inch" (102- or 203-mm) overlay points are above the line of equality.

1 ft = 0.305 m
1 mi = 1.61 km

Figure 84. Graph. LTPP-measured versus MEPDG-predicted

Despite the variations in the quality of predictions among different site factors, predictions of sections with overlays were consistently better than sections without overlays, including the control section. This was surprising because most of the the MEPDG calibration effort was devoted to new pavement conditions.

Rutting

Predicted versus measured rutting data are shown in figure 85 for SPS-6 sections with HMA overlays on JPCP. The results suggest that the rutting model was consistently overpredicting for HMA over cracked and seated JPCP . The results also suggest that MEPDG underpredicts for regular HMA over JPCP slab. This is likely caused by the MEPDG assumption for HMA over cracking and seated pavement. The total rutting in all layers is predicted; thus, some overprediction occurred. For HMA over existing JPCP, the rutting output was only in HMA.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted rutting for Specific Pavement Study (SPS)-6 sections with overlays. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured rutting in millimeters, and the y-axis shows the predicted rutting in millimeters. The individual points are represented by black colored diamond markers for crack or break and seal, white diamond markers for maximum restoration, and crosses for minimum restoration. While all data points for crack or break and seal are mostly above the line of equality, the maximum and minimum restoration overlay points are mostly below the line of equality. In general, the graph resembles a column chart but it has evenly spaced points at 0.02-inch (0.5-mm) rutting intervals and runs parallel to the y-axis.

1 inch = 25.4 mm

Figure 85. Graph. LTPP-measured versus MEPDG-predicted rutting for SPS-6 sections with overlays.

Cracking

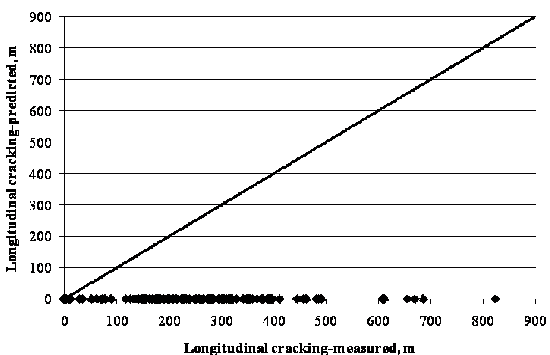
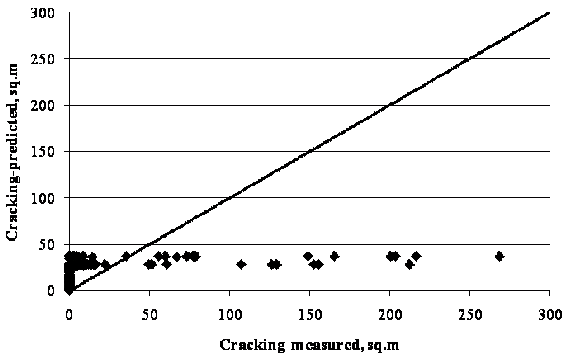
Estimates of longitudinal top-down fatigue cracking and fatigue bottom-up alligator cracking were computed using MEPDG. Predicted versus measured longitudinal fatigue cracking results in wheel paths only are shown in figure 86. The MEPDG software does not predict longitudinal cracking on HMA overlays over JPCP. Total fatigue cracking data (i.e., new cracking originated at the new HMA overlay plus reflective cracking from propagated cracks in the PCC layer) are shown in figure 87. The results suggest that the MEPDG fatigue cracking model may underpredict and overpredict the levels of cracking. Reflective cracking was the only component with predictions higher than zero, as expected.

Several attempts were made to isolate the sections being underpredicted and overpredicted based on climate conditions, pavement condition prior to overlay, or type of treatment, but the results were inconclusive. It was difficult to identify sources of cracking during surveys, and reflective cracking usually was not measured for the LTPP experiments. The confusion on the source of cracking measured in addition to the existing emprical model for reflective cracking incorporated in MEPDG highlights the need for future studies under the LTPP program, particularly to address improvements to the existing model for reflective cracking to be based on reliable data for this type of distress.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted longitudinal cracking for hot mix asphalt (HMA) overlaid Specific Pavement Study (SPS)-6 sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured longitudinal cracking in meters, and the y-axis shows the predicted longitudinal cracking in meters. The individual points are represented by black colored diamond markers. Predicted values for longitudinal cracking are close to zero with measured values ranging from 0 to 2,689.6 ft (0 to 820 m).

1 ft = 0.305 m

Figure 86. Graph. LTPP-measured versus MEPDG-predicted longitudinal cracking for HMA overlaid SPS-6 sections.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted cracking for hot mix asphalt (HMA) overlaid Specific Pavement Study (SPS)-6 sections. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured cracking in square meters, and the y-axis shows the predicted cracking in square meters. The individual points are represented by black colored diamond markers. There is a high concentration of points on and near the y-axis with predicted cracking values ranging from 0 to 430.56 ft2 (0 to 40 m2). The rest of the data points resemble a line parallel to the x-axis at about 430.56 ft2 (40 m2) with measured cracking values as high as 2,906.28 ft2 (270 m2).

1 ft = 0.305 m

Figure 87. Graph. LTPP-measured versus MEPDG-predicted fatigue and reflective cracking for HMA overlaid SPS-6 sections.

Faulting

Trends for MEPDG predicted versus measured faulting are shown in figure 88 for SPS-6 sections without overlay. The results suggest that MEPDG underpredicts faulting for the majority of rehabilitated sections. The sites were grouped by climate conditions; however, the results did not provide any information on possible influence of climate conditions. An attempt was made to isolate pavement surface condition prior to rehabilitation. Predicted versus measured faulting for SPS-6 sections grouped by pavement surface condition is shown in figure 89 and figure 90. Faulting in pavements in fair condition prior to rehabilitation was consistently underpredicted, as suggested in figure 89. Predictions were more accurate for sections with pavements in poor condition prior to rehabilitation (see figure 90).

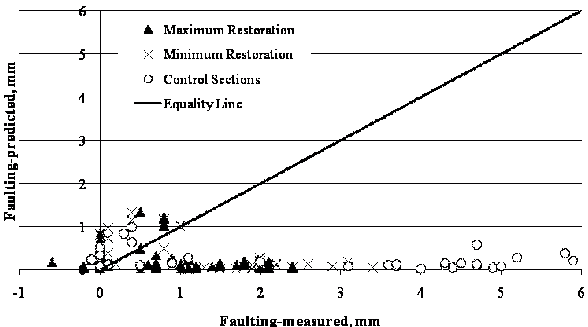
This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted faulting for Specific Pavement Study (SPS)-6 sections without hot mix asphalt (HMA) overlay. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured faulting in millimeters, and the y-axis shows the predicted faulting in millimeters. The individual points are represented by black colored triangles for maximum restoration, crosses for minimum restoration, and circles for control sections. Many of the data points are located near the x-axis with measured faulting values ranging from 0 to 0.234 inches (0 to 6 mm). Some points are also located right above the solid diagonal line with predicted faulting values ranging from 0 to 0.039 inches (0 to 1 mm).

1 inch = 25.4 mm

Figure 88. Graph. LTPP-measured versus MEPDG-predicted faulting for SPS-6 sections without HMA overlay.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted faulting for Specific Pavement Study (SPS)-6 sections in fair condition without hot mix asphalt (HMA) overlay. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured faulting in millimeters, and the y-axis shows the predicted faulting in millimeters. The individual points are represented by black colored triangles for maximum restoration, crosses for minimum restoration, and circles for control sections. Many of the data points are located near the x-axis with measured faulting values ranging from 0 to 0.234 inches (0 to 6 mm). Some points are also located right above the solid diagonal line with predicted faulting values ranging from 0 to 0.039 inches (0 to 1 mm).

1 inch = 25.4 mm

Figure 89. Graph. LTPP-measured versus MEPDG-predicted faulting for SPS-6 sections without HMA overlay with fair pavement condition prior to rehabilitation.

This scatter plot shows Long-Term Pavement Performance (LTPP)- measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted faulting for Specific Pavement Study (SPS)-6 sections in poor condition without a hot mix asphalt (HMA) overlay. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured faulting in millimeters, and the y-axis shows the predicted faulting in millimeters. The individual points are represented by black colored triangles for maximum restoration, crosses for minimum restoration, and circles for control sections. Most of the data points are distributed in two clusters. The first set of points is located directly above the solid diagonal line with predicted faulting values ranging from 0 to 0.039 inches (0 to 1 mm). The second cluster is located near the x-axis with measured faulting values ranging from 0.02 to 0.05 inches (0.5 to 1.2 mm). There are also some sections in poor condition with maximum and minimum restoration with measured faulting values a little over 0.078 and 0.117 inches (2 and 3 mm), respectively, near the x-axis.

1 inch = 25.4 mm

Figure 90. Graph. LTPP-measured versus MEPDG-predicted faulting for SPS-6 sections without HMA overlay with poor pavement condition prior to rehabilitation.

Load Transfer Efficiency

LTE was estimated for SPS-6 sections without HMA overlay using MEPDG. Predicted versus measured data from LTPP SPS-6 sections are plotted in figure 91. The results suggest that the LTE model slightly overpredicted LTE for sections without any rehabilitation (control), but estimates were considered reasonable. The results were better for sections that received some maintenance/rehabilitation work (minimum and maximum). Site conditions were investigated, and no further trends were observed.

This scatter plot shows Long-Term Pavement Performance (LTPP)-measured versus Mechanistic Empirical Pavement Design Guide (MEPDG)-predicted load transfer efficiency (LTE) for Specific Pavement Study (SPS)-6 sections without hot mix asphalt (HMA) overlay. This plot has a solid diagonal line of equality with a slope of 1 going from the lower left to upper right corner. The x-axis shows the measured LTE in percentage, and the y-axis shows the predicted LTE in percentage. The individual points are represented by black colored triangles for maximum restoration, crosses for minimum restoration, and circles for control sections. The data points for maximum and minimum restoration are scattered both above and below the line of equality, while most of the control section points are above the equality line. Measured and predicted values for LTE generally range from 60 to 90 percent for all values.

Figure 91. Graph. LTPP-measured versus MEPDG-predicted LTE for SPS-6 sections without HMA overlay.

Summary and Conclusions

The MEPDG roughness models for both flexible and rigid pavements provided good predictions of rehabilitated sections with and without HMA overlay. There were some biases in the predictions, which could be addressed with local or a revised general calibration. MEPDG tends to underpredict roughness for rigid pavement sections with IRI values above  9.50 ft/mi (1.8 m/km). This bias was more characteristic of sections located in dry and freeze regions.

The HMA rutting model needs further enhancements to further predict permanent deformation accurately in HMA overlay over flexible and rigid pavements. Interestingly, the rutting model overpredicted performance of HMA overlays over crack/break and seat restored rigid pavements and underpredicted for the rest of restoration treatments (saw and seal and minimum and maximum restorations prior to overlays). MEPDG considers the cracked/broken PCC layer as a new granular base layer. Permanent deformation was predicted for the new layer and the subgrade, which is normally the reason for the overprediction of total rutting identified in this study. The rutting model clearly needs calibration before use with overlaid pavements.

The cracking models for HMA overlays, particularly the empirical reflection cracking, need further enhancements to provide more accurate predictions. The models for fatigue cracking (new and reflective) and longitudinal cracking were not capable of predicting consistent and comparable performance with measured values. MEPDG did not predict transverse cracking in any of the SPS-5 or SPS-6 sections, although some transverse cracking was measured during surveys.

 

 

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse | U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101