U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
| Publication Number: FHWA-HRT-12-030 Date: August 2012 |
Publication Number: FHWA-HRT-12-030 Date: August 2012 |
PDF Version (4.44 MB)
PDF files can be viewed with the Acrobat® Reader®
This chapter summarizes the literature review performed to investigate the correlations proposed by researchers and practitioners to estimate mechanical properties of pavement materials from simpler material index or constituent properties. The material types covered in this review are PCC and unbound aggregate and soils.
The literature was compiled from the following sources:
PCC mix mechanical properties such as compressive strength (f'c), flexural strength (also called modulus of rupture), tensile strength (ft), elastic modulus (E), CTE, and drying shrinkage were among the most commonly studied and discussed in the literature, as they directly impact pavement performance. PCC mix constituent properties such as w/c ratio and coarse aggregate characteristics appeared to be the more commonly used properties to predict these PCC mix mechanical properties.
Other PCC properties, such as temperature at set, unit weight, thermal conductivity, heat capacity, and specific heat, which have come into sharper focus since the advent of the MEPDG and other pavement modeling programs such as the FHWA’s HIgh PERformance Concrete PAVing (HIPERPAV®) software, were not very well documented in the literature.(35)
The following discussion summarizes the factors affecting some of the commonly cited PCC mix properties and typical correlations proposed.
Compressive strength of concrete is the most frequently used measure of concrete quality in design and QA during construction. This parameter, most easily determined through a laboratory uniaxial compressive loading test and standardized in ASTM C 39, is considered a fundamental strength property.(36) PCC has a high compressive strength, and most structures are designed to take advantage of this property. The 28-day compressive strength is a widely accepted strength index, especially for initial design. PCC strength increases with time and can affect opening strength, as well as rehabilitation designs in the long term. The compressive strength is also used frequently as an index for other strength types. As will be discussed in chapters 4 and 5, emphasis was placed on developing prediction models for compressive strength in this study.
In a majority of materials, including PCC, strength has been found to correlate strongly with its intrinsic porosity. Although considered a homogeneous material, concrete contains void spaces of various sizes in the matrix and in the interfacial zone (ITZ). Voids in the ITZ are responsible for the development of microcracks in the material. The failure modes initiated in the material vary with the type of loading applied. The formation of cracks in the matrix under a uniaxial compressive load requires greater energy compared to failures resulting from other forms of loading. A stable system of cracks exists in the ITZ up to 50 or 60 percent of the failure loads.
At higher stress levels, cracks initiate and progress through the matrix, combine with those in the ITZ, and a failure plane develops 20 to 30 degrees from the direction of load. The failure is typically more brittle with high-strength concrete.
Concrete strength is influenced by the complex interaction of the characteristics and proportions of the individual materials, the consolidation provided (construction factors), the curing condition, and the rate/type of loading. Ozyildirim and Carino provide a comprehensive summary of the test procedures to determine each strength parameter (i.e., type of loading) and the parameters that are most significant.(37) It can be difficult to isolate the effect of a single parameter because of the inherent interaction and their confounding effects. The following list summarizes the influence of key parameters:
Irick et al. conducted a pilot PRS study in which they developed a comprehensive summary of all PCC material property prediction models. The predictor variables used in that study were generally in agreement with the list and discussion above.(7) Figure 2 illustrates the summary of factors and specific properties that affect concrete strength. In developing predictive models, every effort was made to evaluate the effect of parameters from this list that were available in the LTPP database. Furthermore, unless the data exhibited the effects discussed here, the parameter would not be recognized as significant in the statistical analyses.
The porosity of concrete, which includes paste porosity and ITZ porosity, cannot be determined realistically. Therefore, no empirical correlations exist to compare concrete porosity and strength. Other surrogate parameters that affect porosity or strength have been used to model compressive strength.
Compressive strength has been related mainly to the w/c ratio. Neville reported about Feret’s work in 1896 that correlates mix volumetrics to strength.(40) Abrams’ work proposed a ratio law for concrete strength based on a more thorough investigation of other parameters and stated that the strength of the concrete was solely controlled by the ratio of cement to free water in the plastic mixture (i.e., the w/c ratio) as long as the cement type, conventional aggregates, placement conditions, curing conditions, and test conditions remained constant. (41)
The empirical coefficients relating PCC compressive strength to w/c ratio depend on the units, materials, test methods used, age of testing, and the conditions of validity for Abrams’ law. Further, Abrams suggested the following conclusions:(41)
Research suggests that Abrams’ law is valid, provided that the following assumptions hold:
In 2006, Colak presented a model for strength prediction based on only w/c ratio.(42) However, Abrams’ assumptions are not true, especially in the case of high-strength concrete, for which the mechanical properties of the aggregate become important.(41) However, Alexander and Mindess found that no universal or meaningful mathematical relationships were derived to predict concrete strength as a function of both paste and aggregate variables.(43) This suggests that mix-specific empirical correlations will possibly need to be developed while considering key cement, cement paste, and aggregate attributes of interest to the concrete compressive strength.
The first studies of the effects of aggregates on concrete strength were conducted by Gilkey as well as Bloem and Gaynor.(44,45) Gilkey presented a review of the limitations of the Abrams w/c ratio theory. He proposed that Abrams’ law must be extended to include such parameters as the ratio of cement to aggregate, stiffness and maximum size of aggregate, and surface texture. According to Gilkey, Abrams’ law could be generalized into a series of relationships represented by a family of approximately parallel strength curves.
The work of Bloem and Gaynor concentrated mainly on the effect of maximum size of concrete aggregate on compressive strength.(45) They found that strength decreased as aggregate size increased over the full range of w/c ratio. Their relationships are of limited significance for widespread use because the impact on compressive strength of the different types of aggregates can be larger than impact of maximum size of aggregate.
In the United Kingdom, Kaplan investigated the impact of aggregate surface texture, aggregate shape, and modulus of elasticity on compressive strength.(46) Aggregate strength within the limits of Kaplan’s tests had no effect on concrete strength, which is where the target strength of the mix design is of significance, as discussed previously.
In work performed by Bennett and Khilji in the United Kingdom, an empirical relationship between concrete strength and the following variables was developed: w/c ratio, static modulus of elasticity of coarse aggregate, coarse aggregate/cement ratio, angularity number, and the aggregate impact value.(47) These researchers found that the modulus of elasticity of the coarse aggregate had a considerable effect on the strength, exceeded only by w/c ratio.
De Larrard and Bellock developed a semi-empirical method for defining compressive strength of concrete.(48) They suggested the concept of maximum paste thickness (MPT), which can be interpreted as the mean distance between aggregate particles and is described in terms of three important mix variables: the maximum size of aggregate, the aggregate volume concentration, and packing density of aggregate. They established that the strength of concrete depends on MPT, and they developed the empirical equation between concrete compressive strength and matrix strength, which was determined from the paste strength. According to this equation, for very high matrix strengths, the composite strength of concrete is controlled by the intrinsic strength of the rock. For low matrix strengths (or alternatively very high aggregate strengths), the strength of the composite is proportional to the matrix strength, with coefficients depending on the bond between the paste and the aggregate.
De Larrard and Bellock’s equations, while based on sound concepts and helpful for theoretical strength prediction, do not provide a universally applicable approach to the problem of compressive strength prediction. For example, they do not account for the effects of aggregate elastic modulus, shape, and texture, as in Kaplan’s investigations. Also, De Larrard and Bellock’s results can be applied only to high-strength concrete where it is possible to measure paste strength with a reasonable degree of certainty.
The results of a comprehensive study of compressive strength were presented by Namyong et al.(49) This study used 1,442 compressive strength test results obtained from specimens with a range of w/c ratios and cement/aggregate ratios. Based on the results of correlation analysis, Namyong et al. developed empirical equations for predicting compressive strength of in situ concrete.
Time effects on compressive strength gain or strength at a given time have been predicted by several models. ACI and the Committee Euro-International du Beton (CEB-FIP) provided models to predict strength at a given time after hydration.(50,51) The ACI model is applicable only to moist-cured samples cast with type I cement, and the CEB-FIP model is applicable only for specimens cured at 70 °F. FHWA’s HIPERPAV® concrete compressive strength model is based on generalized Abrams theory.(52) The HIPERPAV® compressive strength prediction model accounts for the influence of w/c ratio, pozzolans, and aggregate contents in addition to concrete age. The main limitation of the HIPERPAV® compressive strength model is that it assumes all the conditions required to apply Abrams’ rule are satisfied. Also, this model was calibrated only for fly ash as the mineral admixture. Wang et al. used historical concrete mix design and strength test data in Iowa and developed statistical models to predict strength and other concrete properties.(53)
Powers’s approach for compressive strength for hardening concrete (time generalization of Abrams’ law) has been used wherein the compressive strength was predicted as a function of the gel/space ratio, which, in turn, was found to be a function of degree of hydration and the w/c ratio.(54) Tango’s model uses the additional time-dependent parameter, the degree of hydration, when considering concrete age.(55) This model was used successfully in the prediction of concrete strength in the Brazilian IPT concrete mixture design method. Irick et al. provided a comprehensive literature summary of models to predict concrete strength parameters.(7)
The equations in figure 3 through figure 7 summarize a few key models for compressive strength, fc. These models are significant from the standpoint of fundamental theories and those that are relevant to the context of the current study.
Where:
k1, k2 = Empirical constants for a mix.
w/c = water/cement ratio.
Where:
K = Empirical constant.
c, w, a = Cement, water, and air content volumetric proportions.
Where:
![[any value] [any value]](images/image015.png) =
Constants.
=
Constants.
Where:
f c(t) = Compressive strength at time, t days.
f c,28 = Compressive strength at 28 days.
t = Time in days.
Where:
A, B, C, D, E, F, G = Empirical constants.
w/b = w/c ratio.
uw = Unit weight.
CMF = Cementitious materials factor.
t = Time after hydration or age in days.
The flexural strength or MR and split tensile strength of concrete are the most commonly used indices to define the tensile capacity of PCC. Concrete is typically not tested under direct tension because the test apparatus and the loading mechanism introduce secondary stresses that are not easy to compensate for. Since the factors that affect these two strength estimates share some similarities in the nature of failure introduced along with a limited set of dissimilarities, the factors affecting their values are quite similar. Like compressive strength, MR is influenced by mix design parameters including w/c ratio, cement type, cement content, and aggregate properties (aggregate type, maximum size, gradation, and surface texture). In general, the material characteristics affect MR in the same manner as compressive strength. However, parameters that affect ITZ porosity are more sensitive to flexural strength. Literature published in the last decade suggests that the most important factor governing concrete tensile capacity is the aggregate matrix bond.(56,57)
The flexural strength of concrete is defined as the maximum tensile strength at rupture at the bottom of a simply supported concrete beam during a flexural test with third point loading, as standardized in ASTM C 78-02.(58) Failure in the region between the loads applied at third points, or the region of maximum moment, is considered to be acceptable for this test. In other words, this test measures the tensile capacity of the material in bending or flexure. MR of a fully supported slab is far greater than the flexural strength of a simply supported beam. MR is the basis for estimating flexural fatigue in concrete. In the MEPDG, the damage calculated for the estimation of transverse cracking is a function of the flexural strength of the concrete. A true estimation of MR, therefore, would improve the accuracy of cracking prediction.
Kaplan developed a regression equation for flexural strength after statistical analysis of test data.(46,59) He associated MR with aggregate elastic modulus, void percents, and surface texture roughness. According to Kaplan, the elastic modulus of the aggregate is the most important factor affecting flexural strength.
The split tensile strength, commonly referred to as the indirect tensile strength or simply the tensile strength of PCC, is estimated using the ASTM C 496-90 test, which involves subjecting a concrete cylinder to compressive loads along two diametrically opposite axial lines.(60) The compressive load applied on the side of a cylindrical specimen causes a uniform tensile stress along the vertical diameter until the specimen fails. The indirect tensile strength is used in the CRCP distress prediction models of the MEPDG. This strength parameter has a direct influence on the transverse crack spacing, which, in turn, affects the crack widths, the load transfer efficiency of the crack, and eventually damage leading to punchout development.
Of all the PCC mechanical properties listed, compressive strength is the easiest and, not surprisingly, the most commonly tested parameter. Consequently, several researchers have developed relationships between this parameter and the three other PCC strength/modulus parameters—flexural strength, tensile strength, and elastic modulus. A summary of the flexural strength models is presented in figure 8 through figure 11, and a summary of the tensile strength correlations to compressive strength is presented in figure 12 through figure 17.
Various researchers have found that the relationship follows a power curve model. This is mainly because as the compressive strength of the concrete increases, the ratio between the tensile strength and compressive strength decreases, as does the ratio between the flexural strength and compressive strength.(39)
Where:
a = 9.0, b = 0.5 (psi).(61)
a = 7.5, b = 0.5 (psi); a = 0.62, b = 0.5 (MPa).(50)
a = 8.3, b = 0.5 (psi).(62)
a = 9.6, b = 0.5 (psi).(63)
a = 11.7, b = 0.5 (psi) (for high-strength mixes).(64)
a = 12.93, b = 0.4543 (psi).(53)
a = 0.3, b = 0.66 (MPa).(51)
a = 2.63, b = 0.66 (psi).(65)
Where:
k2 ranges from 3 to 6 psi. k1 ranges from 0.3 to 0.8 psi.
Where:
MOR(t) = The flexural strength at age t years. MOR28d = The 28-day flexural strength.
Where:
f'sp = Tensile strength. a = 4.34, b = 0.55 (psi).(67)
a = 0.53, b = 0.7 (MPa).(40)
a = 7.11, b = 0.5 (psi) (high strength mixes).(68)
a = 0.89 to 1.7, b = 0.67 to 0.71 (MPa).(See references 69–72.)
a = 1.019, b = 0. 0.7068 (psi).(53)
a = 1.56, b = 0. 0.67 (MPa).(51)
Where:
fck = Compressive strength, MPa.
fcko = 10 MPa.
Where:
a is a correlation coefficient and ranges from 0.48 to 0.68.
Where:
f'sp(t) = Tensile strength at age t years.
f'sp, 28d = Tensile strength at 28 days.
![[any value] [any value]](images/image028.png) = Empirical constants for
a mix design.
= Empirical constants for
a mix design.
Tensile strength is typically linear, with MR and estimated tensile strength being between 0.6 and 0.7 of MR. This is mostly because only a small volume of the material is under tension in the MR test compared to the entire volume in the tensile strength test. Also, the flexural strength test assumes a linear stress strain relationship across the depth of the beam. For very low-strength concretes, the tensile strength is nearly half the flexural strength.
Mallela et al. evaluated these models with the 2000 data release of the LTPP materials data.(16) The following broad conclusions were drawn:
The MEPDG provides a model form to develop strength gain relationships for agencies implementing the procedure.(2) Based on flexural strength data analyzed in the calibration of the MEPDG models, the flexural strength at any age, t (years), can be calculated based on the 28-day strength. This generalized relationship is included in figure 7, and it can be modified for specific mix designs using test data at different ages. Likewise, the tensile strength gain can be calculated using the model form included in figure 17.
Elastic modulus measures material stiffness and is a ratio of the applied stress to measured strain. This is determined using the ASTM C 496-90 test procedure, wherein the chord modulus is measured in a concrete cylinder loaded in longitudinal compression at a relatively slow constant rate.(60) This test procedure also is used to determine Poisson’s ratio.
The concrete elastic modulus is an important variable in pavement design, as it controls the overall slab deflections from traffic loading and slab curling stresses. Historically, in pavement applications, this value has not been rigorously estimated; typical values are assumed because it is perceived to have little effect. However, newer design methods such as the MEPDG have brought the importance of this parameter to the forefront. Generally, PCC elastic modulus increases as compressive strength increases, and it was found that in general, the material characteristics affect the elastic modulus in the same manner as the compressive strength. However, elastic modulus is more sensitive to aggregate characteristics and volumes.
Early works in this area established that concretes having the same compressive strength may have different moduli of elasticity if different aggregates are used. Additionally, concretes of different proportions may have different compressive strength for the same elastic modulus. Finally, for equal compressive strength, the elastic modulus increases with increasing aggregate/cement ratio.(59,73)
The properties of aggregates also influence the modulus of elasticity—the higher the modulus of elasticity of the aggregate, the higher the modulus of the concrete.(74) The shape of coarse aggregate particles and their surface characteristics may also influence the value of the modulus of elasticity of concrete.(40) The aforementioned are very significant findings, suggesting that the strength-modulus relationship should be mixture specific.
Mathematical expressions to predict elastic modulus have been developed based on concrete being modeled as a two-phase material, a matrix phase and aggregate phase. (See references 75–79.)
Several relationships between elastic modulus and compressive strength are presented in the literature. (See references 39, 40, 67, and 80.) All these relations are valid for specific samples of data and are affected by the condition of the specimen at the time of testing.
Extensive pavement-specific studies to predict material properties from index properties were conducted in the 1990s as part of FHWA’s PRS development for concrete pavements.(8) Mix design factors were compared against PCC strength and modulus to evaluate the effects of coarse aggregate type, cement content, air content, and w/c ratio. It was found that elastic modulus and flexural strength were most sensitive to a change in w/c ratio. The analyses conducted with the 2000 release of LTPP materials data showed that the compressive strength-static elastic modulus relationships produced no consistent trend.(16)
The relationship between modulus of elasticity and strength also depends on the mix proportions and on the age of the specimen. At later ages, the modulus increases more rapidly than strength.(40)
In general, the elastic modulus of concrete is influenced by the stiffness of the paste and aggregate phases, their volume concentrations, and interface characteristics or the ITZ. The stiffer the individual phases, the higher the elastic modulus. Concrete elastic modulus also increases with increases in the stiffer phase (usually the aggregate). Also of significance is the moisture state of the specimen. For a given aggregate, elastic modulus increases with the strength of the concrete. The significant influence of aggregates on concrete elastic modulus was confirmed in a study of 23 aggregate types conducted by Alexander and Davis.(81,82) Each aggregate type produces a different age-dependent relationship. Likewise, Noguchi et al. developed a model for high-strength concrete mixes as a function of aggregate type and admixtures used.(83)
The various models developed for the prediction of
elastic modulus as well as the MEPDG recommended model for the estimation of
modulus at any age are presented in figure 18 through figure 26. In these equations, Ec is the PCC secant elastic modulus in psi (GPa),
![[any value] [any value]](images/image029.png) is
the PCC unit weight in pounds per cubic foot (kg/m3), and f'c
is the PCC compressive strength of a standard 5.85- x 11.7-inch cylinder in psi.
is
the PCC unit weight in pounds per cubic foot (kg/m3), and f'c
is the PCC compressive strength of a standard 5.85- x 11.7-inch cylinder in psi.
Where:
a = 57,000, b = 0.5 (psi).(50)
a = 275,538, b = 0.33(psi).(51)
a = 77,173, b = 0.46(psi).(71,72)
a = 80811, b = 0.4659(psi).(53)
Where:
a = 9.1, b = 2,300, c = 0, d = 0.33.
a = 9.5, b = 2,400, c = 8, d = 0.33.
or
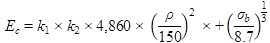 (Units in ksi)
(Units in ksi)
Where k1 and k2 are constants, and their values depend on the coarse aggregate type and the admixture.
CTE has received much attention recently since it appears to have a huge impact on the pavement design methodology proposed in the MEPDG. Its importance has been recognized since Westergaard’s 1927 study from a pavement analysis standpoint.(86) The concrete CTE parameter directly influences the magnitudes of temperature-related pavement deformations. These deformations, in combination with the restraint offered by the base layer and slab weight, affect the resulting curling stresses in the slab. CTE is found to be most influenced by the coarse aggregate rock type as well as the internal relative humidity of the paste.
A protocol for CTE measurement of concrete, AASHTO TP 60, Standard Test Method for the Coefficient of Thermal Expansion of Hydraulic Cement Concrete, was adopted and the method is standardized now as a full AASHTO test procedure, AASHTO T 336, which has modified calibration requirements consistent with the 2010 LTPP data release.(24,87) The older AASHTO TP 60 should be used with earlier CTE data releases.(24)
Mallela et al. presented results of CTE testing conducted by FHWA as part of the LTPP material testing.(15) CTE of the concrete was found to vary widely depending on the predominant aggregate type used in the concrete. This was in agreement with the CTE values reported by Irick et al. by aggregate type.(7) The Mississippi Department of Transportation, in its efforts to implement the MEPDG, conducted PCC material property tests, including CTE on a range of mixes used in Mississippi.(88) In addition to several PCC material test results, it also presented CTE test results. In general, the effect of aggregate type was significant on reported CTE values.
CTE of concrete is predicted empirically by CTE of cement paste and aggregate. Aggregate type has the greatest influence on the value of thermal expansion due to the high volume content of coarse and fine aggregate in concrete.(89,90) Neekhra developed prediction models to estimate the CTE of coarse aggregates and PCC based on the CTE of their individual components.(91) Individual components are defined as the individual minerals for the estimation of aggregate CTE and mortar-aggregate phases for the estimation of PCC CTE. (The estimation of aggregate CTE is not of particular relevance to this study, and thus this review discusses only Neekhra’s findings regarding the CTE of PCC.) PCC CTE is predicted based on the percent volume fraction, CTE, and modulus of elasticity of coarse aggregates and the mortar. In deriving the CTE model, Neekhra assumed that the PCC follows the Hirsch composite model, and the predictions are based on a 50-50 split in the fraction of material in series and parallel alignments. CTE measurements were made using the dilatometer, and the model was verified using nine different mixes that contained different aggregate types. A level 2 equation based on mix volumetrics has been proposed in the MEPDG to predict PCC.(2) The models are provided in figure 27 and figure 28.
![[any value] [any value]](images/image003.png) according to Neekhra.(91)
according to Neekhra.(91)Where:
![[any value] [any value]](images/image041.png) and
and ![[any value] [any value]](images/image042.png) = CTE of mortar and
aggregate.
= CTE of mortar and
aggregate.
Vm and Va = Volume fraction of mortar and aggregate.
Em and Ea = Elastic modulus of mortar and aggregate.
X = Relative proportion of material conforming with the upper and lower bound solution (assumed as 0.5).
Note that X = 0 implies series arrangement, and X = 1 implies parallel arrangement of constituent phases in the Hirsch model.
![[any value] [any value]](images/image004.png) according
to NCHRP.(2)
according
to NCHRP.(2)Where:
![[any value] [any value]](images/image044.png) = CTE of
PCC, aggregate, mortar, and paste.
= CTE of
PCC, aggregate, mortar, and paste.
Vagg and Vpaste = Volume fraction of aggregate and paste.
Drying shrinkage of hardened concrete is an important factor affecting the performance of PCC pavements. The magnitude of drying shrinkage depends on numerous factors, including water per unit volume, aggregate type and cement, ambient relative humidity and temperature, and curing conditions.(40) The size and grading of aggregate influences the magnitude of shrinkage. Larger aggregate permits the use of a leaner mix and results in lower shrinkage. Clay minerals in the -200 fraction can also increase shrinkage.
Powers demonstrated a significant impact of aggregate volume content on concrete shrinkage.(92) For the high values of aggregate content, concrete shrinkage was small in comparison with cement paste shrinkage. In general, sandstone aggregates tend to produce higher shrinkage in concrete than other aggregates. However, Troxell et al. demonstrated that it is not possible to generalize the effects of different aggregate types on concrete shrinkage.(93)
The current ACI equation for ultimate shrinkage is based on a large database of mix designs and is a function of cement type, concrete strength, and curing practices.(14,94) This equation has been incorporated into the MEPDG and HIPERPAV®.(2,35)
The LTPP database does not contain shrinkage test results; therefore, within the scope of the current project, no prediction models were developed for PCC shrinkage.(5) Consequently, the various shrinkage models are not discussed in detail in this report. However, it is an important parameter and influences the performance of CRCP and JPCP.