U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

 
REPORT
This report is an archived publication and may contain dated technical, contact, and link information
Back to Publication List        
Publication Number:  FHWA-HRT-15-080    Date:  February 2016
Publication Number: FHWA-HRT-15-080
Date: February 2016

 

Synthesis and Evaluation of The Service Limit State of Engineered Fills for Bridge Support

CHAPTER 3.
LITERATURE REVIEW OF PREVIOUS WORK IN ENGINEERED

 

3.1 Overview of Load Deformation Data Catalog of Engineered Fills for Bridge Supports

Various factors may affect the behavior of bridge supports using engineered fills. They include the following:

The performance of bridge supports using engineering fills can be characterized by the following:

In this chapter, the factors that affect the behaviors of shallow foundations are synthesized based on the published results in the literature. They include factors affecting the settlement of shallow foundations with and without reinforcement and factors affecting vertical and lateral deformations of bridge piers and abutments using engineered fills. Further, the effects of transient loads on deformations of bridges supports on granular soils and the determination of stress distributions in granular soils under shallow foundations are reviewed. Based on the literature review, a load-deformation data catalog was compiled into an unpublished Microsoft® Excel spreadsheet.

3.2 Synthesis of Factors Affecting Settlement of Shallow Foundations

Effect of Relative Density of Soil on Settlement of Shallow Foundations

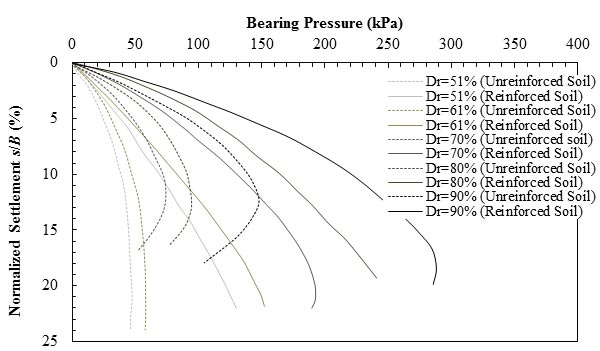
Fragaszy and Lawton performed a series of laboratory model tests designed to determine the influence of soil relative density (DR) on the load-settlement behavior of reinforced sand.(53) The uniformly graded native sand was reinforced with three layers of aluminum foils in all tests. As figure 5 shows, in all cases, the ultimate bearing capacity increased with increasing DR. Additionally, the load-settlement behavior of the strip footings on reinforced soil was stiffer than those bearing on unreinforced soil at the same relative density. The results show that with a 10 percent increase in DR, at 14.5 psi (100 kPa) pressure, the settlement of the foundation decreased by about 20 percent. By reinforcing the soil, the ultimate bearing capacity of the foundation increased at least 60 percent at a ratio of settlement of foundation to its width (s/B) of 10 percent. Note that the increase in confinement with the addition of reinforcement layers suppressed the dilative behavior, as observed through the suppressed peak in load-settlement response. Basudhar et al. conducted an experimental study on circular footings resting on sand reinforced with geotextiles.(54) They concluded that the immediate settlement of the foundation decreased with an increase in DR (see figure 6).

This graph shows the results of experiments on the effect of soil relative density of the reinforced and unreinforced soil on the load-settlement behavior of the foundation. The y-axis shows normalized settlement (s/B) from 0 to 25 percent, and the x-axis shows bearing pressure from 0 to 400 kPa (where 1 kPa equals 0.145 psi). The plot has 10 curved lines leading from the origin. Five solid lines show the experimental results on reinforced soil; the ultimate bearing pressure for this group is equal to 130, 150, 190, 240, and 290 kPa corresponding to 51, 61, 70, 80, and 90 percent soil relative density, respectively. Five dashed lines show the experimental results on unreinforced soil; the ultimate bearing pressure for this group is equal to 45, 60, 75, 95, and 150 kPa corresponding to 51, 61, 70, 80, and 90 percent soil relative density, respectively. In all cases, the foundation settlement decreases by increasing the relative density of the soil.
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Fragaszy and Lawton.(53)

Figure 5. Graph. Load-settlement results on unreinforced and reinforced sand.

This graph shows the results of an experimental study on circular footing resting on reinforced sand with different relative densities. The y-axis shows footing settlement from 0 to 25 mm, and the x-axis shows vertical stress from 0 to 200 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has three lines leading almost linearly from the origin to their ultimate pressures, which are about 135, 160, and 170 kPa for relative densities equal to 45, 73, and 84 percent, respectively. The corresponding footing settlements for these three experiments are 19, 18, and 18 mm, respectively, at their ultimate pressures.
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Basudhar et al.(54)

Figure 6. Graph. Load-settlement results for different relative densities.

Effect of N on Settlement of Shallow Foundations

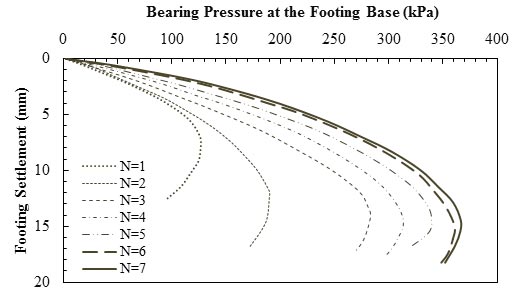
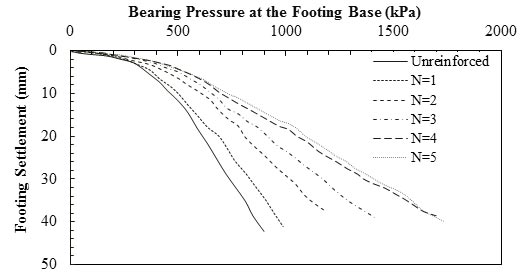
Omar et al. conducted a series of laboratory model tests on strip and square foundations supported by sand reinforced with geogrid layers.(55) As their results in figure 7 and figure 8 show, for similar values of applied load, the settlement of footings bearing on reinforced soil was lower than that on unreinforced soil. For tests with a strip foundation, when N increased from 1 to 3, the ultimate bearing load doubled, while the settlement at its respective ultimate load also almost doubled. At each applied pressure, the amount of settlement decreased with increasing N. for N greater than or equal to 4, the settlement at ultimate bearing load remained practically constant, indicating there is an optimum N beyond which the settlement at ultimate bearing load has insignificant improvement. It should be considered that based on the study by Omar et al., the effective depth of reinforcement is about 2B for strip foundations.(55) Therefore, in their experiment, by having u/B = h/B = 0.33 (the notations are shown in figure 4), reinforcements with N greater than or equal to 7 are placed out of the influence zone.

This graph shows the experimental results on strip foundation placed on reinforced soil for u/B = h/B = 0.333 and b/B = 10, where u is embedment depth of top geogrid layer, B is the width of foundation, h is the spacing of reinforcement layers, and b is the length of reinforcement layers below foundation. The y-axis shows footing settlement in mm from 0 to 20 mm, and the x-axis shows bearing pressure at footing base from 0 to 400 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has seven lines for different numbers of reinforced layers (N) from 1 to 7. When N increased from 1 to 3, the ultimate bearing load more than doubled (from 125 to 280 kPa), while the settlement at its respective ultimate load also almost doubled (from 7 to 14 mm). The ultimate bearing pressure of the foundation is equal to 125, 190, 280, 315, 340, 360, and 365 kPa as N increases from 1 to 7. At each applied pressure, the amount of settlement decreases with increasing N; for N greater than or equal to 4, the settlement at ultimate load remains practically constant at 15 mm.
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Omar et al.(55)

Figure 7. Graph. Load-settlement results for strip footing for u/B = h/B = 0.333, b/B = 10.

This graph shows the experimental results on square foundation placed on reinforced soil for u/B = h/B = 0.333 and b/B = 6, where u is embedment depth of top geogrid layer, B is the width of foundation, h is the spacing of reinforcement layers, and b is the length of reinforcement layers below foundation. The y-axis shows footing settlement from 0 to 6 mm, and the x-axis shows bearing pressure at footing base from 0 to 250 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has six lines for different number of reinforced layers (N) that vary from 1 to 6. The ultimate bearing pressure of the foundation is equal to 90, 135, 160, 180, 185, and 190 kPa as N increases from 1 to 6. The settlement at ultimate load remains practically constant between 3 and 4 mm.
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Omar et al.(55)

Figure 8. Graph. Load-settlement results for square footing for u/B = h/B = 0.333, b/B = 6.

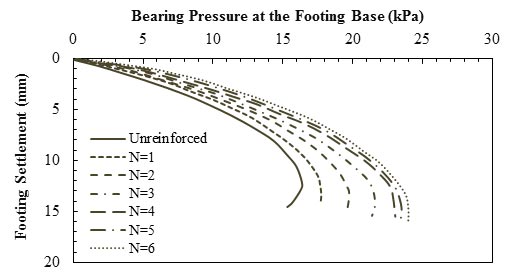
Chen et al. investigated the behavior of square foundations on geosynthetic-reinforced clayey soil with a PI of 15 percent using laboratory model footing tests.(56) The model footings used in the tests were steel plates with dimensions of 5.98 by 5.98 by 1 inch (152 by 152 by 25.4 mm) (width by length by thickness). The model tests were conducted in a 4.92- by 2.98- by 2.98-ft (1.5- by 0.91- by 0.91-m) (length by width by depth) steel test box. The testing procedure was performed according to the ASTM D 1196-93, where the load increments were applied and maintained until the rate of settlement was less than 0.001 inch/min (0.03 mm/min) for 3 min consecutively.(57) The results, plotted in figure 9, show that by increasing N, the amount of settlement at each applied pressure decreased up to N = 4. For N greater than or equal to 4, settlement of square foundations did not increase with additional reinforcement layers. This again indicates there is an optimum N beyond which the settlement has insignificant improvement. It should be noted that based on Chen et al., the effective depth of reinforcement is about 1.5B for geogrid reinforced clay.(56) Therefore, in the experiment by Chen et al., by having u/B = h/B = 0.33, reinforcements with N greater than or equal to 7 are placed out of the influence zone.(56)

This graph shows the experimental results for square foundation on unreinforced and reinforced soil with polypropylene (PP) layers. The y-axis shows footing settlement from 0 to 50 mm, and the x-axis shows bearing pressure at footing base from 0 to 2,000 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has six lines that lead from the origin and represent the load-settlement behavior of foundation placed on unreinforced soil and reinforced soil with different numbers of reinforcements (N) numbered from 1 to 5. By increasing N, the amount of settlement at each applied pressure decreases. For example, at 750 kPa of applied pressure, the settlement of the foundation is about 30 mm for unreinforced soil and 25, 15, 14, 12, and 10 mm for reinforced soil with N equal to 1 to 5, respectively.
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Chen et al.(56)

Figure 9. Graph. Load-settlement results for square footing on unreinforced and reinforced soil with polypropylene (PP) geogrid layers.

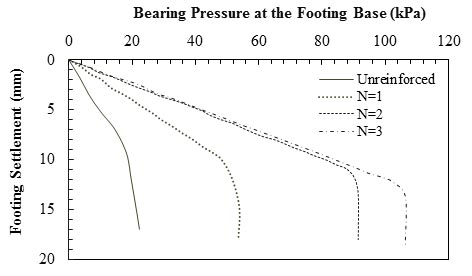
Das et al. conducted laboratory model tests to investigate the ultimate bearing capacity of surface strip foundations on geogrid reinforced sand and clay.(58) Each foundation was made of an aluminum plate with dimensions of 3 by 12 inches (76.2 by 304.8 mm) (B × L). Bearing capacity tests were conducted in two boxes, each with internal dimensions of 3.61 by 0.98 by 2.95 ft (1.1 by 0.3 by 0.9 m) (length by width by depth). The results show that the inclusion of geogrid reinforcement increased the load per unit area that could be carried by a foundation at any given settlement level. This is true for the tests in both sand and clay. As figure 10 shows, the foundation settlement decreased with the increase of reinforcement layer until N = 5. When N was greater than 5, the foundation settlement no longer decreased with an increase of the reinforcement layers. The results may be due to the fact that additional reinforcement layers were placed below the effective depth of reinforcement that was about 2B for strip footing in sandy soil.

This graph shows the results of experiments on strip foundation placed on a reinforced sandy soil for u/B = 0.4, h/B = 0.33, and b/B = 4, where u is embedment depth of top geogrid layer, B is the width of foundation, h is the spacing of reinforcement layers, and b is the length of reinforcement layers below foundation. The y-axis shows footing settlement from 0 to 20 mm, and the x-axis shows bearing pressure at footing base from 0 to 30 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has seven lines that lead from the origin and represent the load-settlement behavior of foundation placed on unreinforced soil and reinforced soil with different numbers of reinforcements (N) from 1 to 6. The foundation settlement at each applied load decreases with an increase in N. For example, at 16 kPa of applied pressure, the settlement of the foundation is about 12 mm for unreinforced soil and 10, 8, 7, 6, 6, and 5 mm for reinforced soil with N equal to 1 to 6, respectively.
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Das et al.(58)

Figure 10. Graph. Load-settlement results for sandy soil for u/B = 0.4, h/B = 0.33, and b/B = 4.

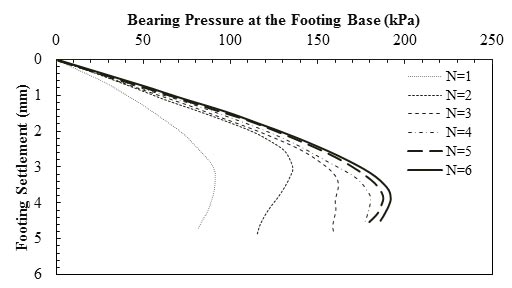
Basudhar et al. conducted an experimental study on circular footings resting on sand reinforced with geotextiles.(54) They concluded that with an increase in N, the settlement gradually decreased in rate. As figure 11 shows, when N is greater than or equal to 2, the foundation settlement no longer decreased with an increase of the reinforcement layers, with the exception of the settlement at ultimate capacity. For the test with three layer of reinforcement, the geotextile was placed at depths of 0.25B, B, and 2B below the base of the footing. By considering the results presented in section, the effective depth of reinforcement was less than 2B for square foundation; therefore, layer 3 and the additional layers were placed outside the influence zone and no longer affected the foundation settlement.

This graph shows the experimental results of experiments on circular footings resting on a sandy soil with 1.18-inch (30-mm)-diameter circular footing. The y-axis shows footing settlement from 0 to 20 mm, and the x-axis shows bearing pressure at footing base from 0 to 120 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has four lines leading almost linearly from the origin to their ultimate pressure which is about 20 kPa for unreinforced soil and 50, 90, and 105 kPa for reinforced soil with one, two, and three layers of reinforcements, respectively. The corresponding settlements for these pressures are 10, 11, 12, and 14 mm, respectively.
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Basudhar et al.(54)

Figure 11. Graph. Load-settlement results for 1.18-inch (30-mm)-diameter circular footing.

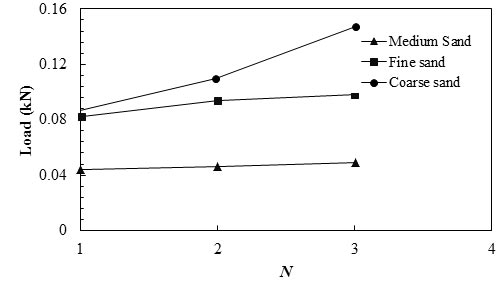
Phanikumar el al. performed a series of laboratory plate load tests on geogrid reinforced sand beds.(59) Properties of the test sands are presented in table 5. Figure 12 shows that at certain settlements, the bearing load needed to reach that settlement was also affected by N and soil types.

Table 5. Properties of test sands.(59)
Property Fine Sand Medium Sand Coarse Sand
Dry unit weight (at DR = 50 percent) (kN/m3) 15.2 14.9 14.7
Maximum aggregate size (dmax) (mm) 0.425 2.36 4.75
Particle diameter at which 10 percent of the sample is finer, by mass (D10) (mm) 0.25 0.59 1.3
Internal Φ* (degree) 32 35 40
Coefficient of uniformity 1.4 1.995 2.07
Coefficient of curvature 1.17 1.12 1.25
1 kN/m3 = 6.37 lbf/ft3
1 inch = 25.4 mm
*The internal Φ of the test sands was determined by performing direct shear tests. The test sands were compacted at their respective dry unit weights corresponding to a relative density of 50 percent.

 

This graph illustrates the effect of number of reinforcement layers on the bearing load to reach a settlement of 0.02 inch (0.5 mm). The y-axis shows load from 0 to 0.16 kN (where 1 lbf equals 0.0044 kN), and the x-axis shows number of reinforcement layers (N) from 1 to 4. The plot has three lines representing medium sand, fine sand, and coarse sand. The required load for a foundation settlement of 0.5 mm (where 1 mm equals 0.039 inch) placed on the course sand is equal to 0.087, 0.110, 0.148 kN for N equal to 1, 2, and 3, respectively. The required load for a foundation settlement of 0.5 mm placed on the fine sand is equal to 0.082, 0.094, and 0.098 kN for N equal to 1, 2, and 3, respectively. The required load for a foundation settlement of 0.5 mm placed on the medium sand is equal to 0.044, 0.046, and 0.049 kN for N equal to 1, 2, and 3, respectively.
1 lbf = 0.0044 kN
Note: This figure was created by FHWA after Phanikumar et al.(59)

Figure 12. Graph. Effect of number of geogrids on the load required for a settlement of 0.02 inch (0.5 mm).

Results of the effect of different numbers of reinforcement on the behavior of foundation placed on reinforced sand with phosphor-bronze layers are plotted in figure 13.(60) The results also show the decreasing trend of settlement with the increasing N at two ratios of reinforcement: L versus B.

This graph shows the experimental results of strip and square footings resting on a reinforced soil. The y-axis shows settlement from 0 to 16 mm, and the x-axis shows applied pressure from 0 to 350 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has six curved lines leading from the origin: one layer of reinforcement with L/B equal to 6 (where L/B is the ratio of length of reinforcement layer to foundation width), two layers of reinforcement with L/B equal to 6, three layers of reinforcement with L/B equal to 6, one layer of reinforcement with L/B equal to 1, two layers of reinforcement with L/B equal to 1, and three layers of reinforcement with L/B equal to 1;. The ultimate pressure for the square footing is 95 kPa (at 8 mm settlement), 150 kPa (at 8 mm settlement) and 185 kPa (at 9 mm settlement) with one, two, and three layers of reinforcement, respectively. The ultimate pressure for the strip footing is 117 kPa (at 7 mm settlement), 160 kPa (at 10 mm settlement), and 270 kPa (at 12 mm settlement) with one, two, and three layers of reinforcement, respectively.
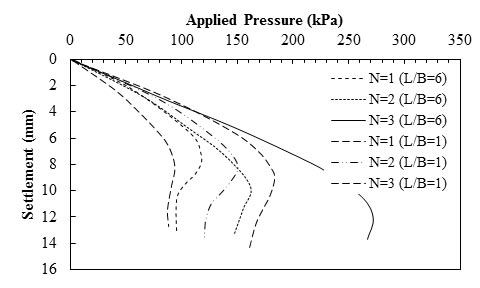
1 inch = 25.4 mm
1 psi = 6.89 kPa

Figure 13. Graph. Load-settlement results for different numbers of metallic reinforcement.

 

Effect of L and Tf of Reinforcement on Settlement of Shallow Foundations

Results from laboratory model tests conducted by Latha and Somwanshi are plotted in figure 14.(61) The results show that with an increase in b, the magnitude of ultimate bearing capacity of foundations on reinforced soil increased, and settlement decreased.

This graph shows load-settlement results for different widths of geonet where layers of reinforcement (N) equals 4, and d equals 2B, where d is the depth of bearing bed reinforcement and B is the foundation width. The y-axis shows normalized settlement from 0 to 20 percent, and the x-axis shows bearing pressure at footing base from 0 to 700 kPa (where 1 kPa equals 0.145 psi). The plot has four curved lines: unreinforced, b/B equal to 4 (where b/B is the ratio of length of reinforcement to foundation width), b/B equal to 5, and b/B equal to 5.93. The curve for the unreinforced soil leads non-linearly from the origin to bearing pressure of 270 kPa with a normalized settlement about 15 percent. The other three curves lead almost linearly from the origin to their ultimate pressure which is about 540, 590, and 630 kPa for reinforcement lengths 4, 5, and 5.93 times the foundation width, respectively. The corresponding footing settlements for these three experiments are 8.5, 10, and 8.5 mm (where 1 mm equals 0.039 inch), respectively, at the ultimate pressure.
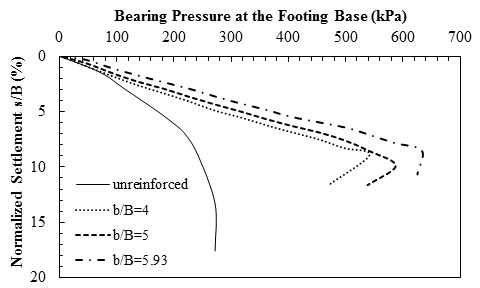
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Latha and Somwanshi.(61)

Figure 14. Graph. Load-settlement results for different widths of geonet (N = 4, d = 2B).

Elton and Patawaran conducted an experimental study on reinforced soil specimens to evaluate the effects of Tf of geotextiles on the stress-strain relationship of reinforced soil.(62) The properties of the six geotextile used in their experiments are presented in table 6. Figure 15 shows the unconfined compression test results. Three transducers on top of the steel loading plate measured vertical displacements. As the results show, the curve initially reached its peak strength at approximately 3 to 8 percent strain, had a decrease in some strength, and then gradually increased back to reach a second peak before finally decreasing sharply. The peak strength and the corresponding strain of the specimens increased as reinforcement strength increased.

Table 6. Geotextile properties.(62)
Property Geotextile Type (G)
G4 G6 G8 G12 G16 G28
Mass per area (g/m2) 135.64 203.46 271.28 406.92 542.56 949.48
Wide-width machine direction strength (kN/m) 9.0 14.0 14.5 18.6 20.1 24.9
Wide-width cross-machine direction strength (kN/m) 14.4 19.3 19.8 20.3 22.9 21.7
1 g/m2 = 2.05 ´ 10-4 lb/ft2
1 kN/m = 68.5 lbf/ft

 

This graph shows the results of an experimental study on reinforced soil specimens to evaluate the effects of tensile strength of geotextiles on the stress-strain relationship of reinforced soil. The y-axis shows stress from 0 to 600 kPa (where 1 kPa equals 0.145 psi), and the x-axis shows vertical strain from 0 to 30 percent. The plot has six curved lines that represent results of specimens reinforced with geotextiles with different wide-width strengths labeled G4, G6, G8, G12, G16, and G28. The curve initially reaches its peak strength at approximately 3 to 8 percent strain, loses some strength, and then gradually increases and reaches a second peak before finally decreasing sharply. The peak strength for different specimens varies between 230 and 450 kPa and increases as reinforcement strength increases.
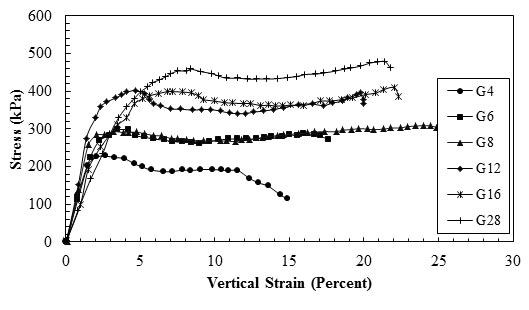
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Elton and Patawaran.(62)

Figure 15. Graph. Stress-strain relationship of reinforced soil.

Adams and Collin conducted five laboratory experiments on reduced-scale piers as part of an FHWA research project.(41) Of the five experiments, one was unreinforced, and the others were reinforced with different reinforcement spacing and Tf. As the results in figure 16 show, the specimen with spacing of 0.66 ft (0.2 m) and lower wide width strength of 1,439 lbf/ft (21 kN/m) could withstand higher stresses compared to the specimen with 1.31-ft (0.4-m) spacing and higher wide width strength of 4,797 lbf/ft (70 kN/m) at any given strain. Therefore, they concluded that the reinforcement spacing played a more important role than the reinforcement strength.

This graph shows the experimental results of reduced-scale piers with different reinforcement spacings and tensile strengths. The y-axis shows stress from 0 to 500 kPa (where 1 kPa equals 0.145 psi), and the x-axis shows vertical strain from 0 to 7 percent. The plot has five curved lines that represent the results for one unreinforced pier and four reinforced piers with different reinforcement spacing and wide-width strengths. The unreinforced specimen can tolerate 32 kPa pressure with 0.6 percent vertical strain. The pier with vertical spacing of 0.4 to 0.6 m and wide-width strength of 70 kN/m (where 1 ft equals 0.305 m, and 1 kN/m equals 68.5 lbf/ft) can withstand maximum stress of 167 kPa at 2.3 percent strain. The pier with vertical spacing of 0.4 m and wide-width strength of 70 kN/m can withstand maximum stress of 22 kPa at 1.9 percent strain. The pier with vertical spacing of 0.2 m and wide-width strength of 21 kN/m can withstand maximum stress of 304 kPa at 2.3 percent strain. The pier with vertical spacing of 0.2 m and wide-width strength of 70 kN/m can withstand the maximum stress of 456 kPa at 6.6 percent strain.
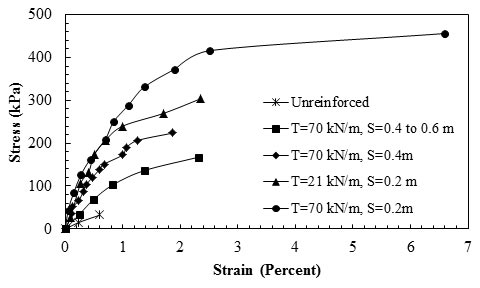
1 psi = 6.89 kPa
1 kN/m = 68.5 lbf/ft
1 ft = 0.305 m
Note: This figure was created by FHWA after Adams and Collin.(41)

Figure 16. Graph. Stress-strain relationship of the mini-pier experiments.

Abu-Hejleh et al. conducted an assessment of the new Founders/Meadows Bridge near Denver, CO, which was completed in July 1999.(63,64) The study focused on the performance and behavior of the GRS system under service loads. Three sections of the GRS system were instrumented to measure movements of the front GRS wall, settlement of the bridge footing, and differential settlements between the bridge abutment and the approaching roadway. The backfill soil used in this project was a mixture of gravel (35 percent), sand (54.4 percent), and fine-grained soil (10.6 percent). The backfill soil was classified as well-graded silty sand per ASTM D 2487 and as stone fragments, gravel, and sand (A-1-B (0)) per AASHTO M145-91.(65,66) The average unit weight and dry unit weight of the compacted backfill soil as measured during construction were 140.6 and 133.7 lb/ft3 (22.1 and 21 kN/m3), respectively, and the water content was 5.6 percent. Results of large direct shear and large triaxial tests showed a Φ of 47.7 and 39.5 degrees and c of 16.06 and 5.73 psi (110.7 and 39.5 kPa), respectively, for the direct shear and triaxial tests. Three grades of geogrid reinforcements were used in this project: uniaxial (UX) 6 below the foundation and UX 3 and UX 2 behind the abutment wall. Table 7 summarizes the ultimate strength and the long-term design strength (LTDS) for these geogrids.

Table 7. Placed geogrid strength.(64)
Geogrid Type and Notation Ultimate Strength (kN/m) LTDS (kN/m)
UX 6 157.3 27
UX 3 64.2 11
UX 2 39.3 6.8
1 kN/m =68.5 lbf/ft

Data were collected during construction of the GRS walls, during placement of the bridge superstructure, and during the 18 mo after opening the bridge to traffic. The results are presented in table 8 and show excellent performance of the GRS structure. The monitored overall displacements were smaller than those expected in the design and allowed by performance requirements, there were no signs for development of the bridge bump problem or of any structural damage, and post-construction movements became negligible within a year after opening the bridge to traffic.

Table 8. Summary of the maximum displacements of the front wall facing and of the settlements of the bridge abutment footing.
Types of Maximum Movements Induced Only by GRS Wall Construction Induced Only by Placement of Bridge Superstructure (115-kPa Surcharge) Induced Only While Bridge in Service (150-kPa Surcharge)
6 Mo 12 Mo 18 Mo
Maximum outward displacement of the front wall facing (mm) 12 10 8 12 13
Maximum settlement of the leveling pad supporting the front wall facing (mm) 8 7 4 5 5
Maximum bridge abutment footing settlement (mm)   13 7 11 10
Percent maximum settlement of bridge abutment of wall height (percent)   0.29     0.17
1 kPa = 0.145 psi
1 inch = 25.4 mm
Note: This table was created by FHWA after Abu-Hejleh et al.(64) Blank cells indicate no value was recorded.

Huang and Tatsuoka used different types of metal strips to reinforce the soil beneath a shallow foundation.(60) Figure 17 shows the results from laboratory model tests reinforced with phosphor-bronze strips. The results show that with an increase in L, the magnitude of the settlement in each applied load decreased. However, this decrease was not proportional to the increase in L. For example, under 4,177 psf (200 kPa) of applied pressure, the settlement of the foundation was the same for two different reinforcement lengths of L/B = 3.5 and L/B = 6.

This graph shows the experimental results of foundation placed on reinforced soil where the number of reinforcement layers (N) equals 3. The y-axis shows settlement from 0 to 16 mm, and the x-axis shows applied pressure from 0 to 400 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has four curved lines for L/B equal to 1, 2, 3.5, and 6, where L is the length of the reinforcement, and B is the width of the foundation. All the curves lead almost linearly from the origin to their ultimate pressure which is about 180, 220, 260, and 310 kPa, respectively. The corresponding footing settlements for these four experiments are 9, 11, 10, and 12 mm, respectively at their ultimate pressures.
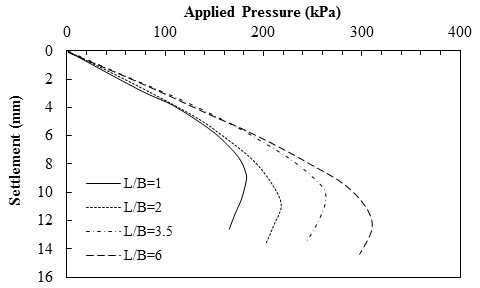
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Huang and Tatsuoka.(60)

Figure 17. Graph. Load-settlement results for different reinforcement lengths (N = 3).

Effect of B on Settlement of Shallow Foundations

Das and Omar conducted an experimental study on surface strip foundations on geogrid- reinforced sand.(67) As shown in figure 18, they concluded that the settlement at the ultimate bearing capacity increased with a decrease in B. The figure also revealed insignificant effects of footing size on settlement under bearing pressures less than approximately 6,266 psf (300 kPa). It is noted that these observations were obtained in small-scale experiments.

This graph shows load-settlement results in reinforced sand where soil relative density (DR) equals 75 percent. The y-axis shows footing settlement from 0 to 35 mm, and the x-axis shows bearing pressure at the footing base from 0 to 500 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has five curved lines that represent the results of five foundations with different widths leading non-linearly from the origin. The ultimate pressures are about 315, 370, 385, 395, and 420 kPa for foundation width equal to 50.8, 76.2, 101.6, 127, and 177.8 mm, respectively. The corresponding footing settlements for these five foundations are 12, 17, 21, and 25 mm, respectively, at their ultimate pressures.
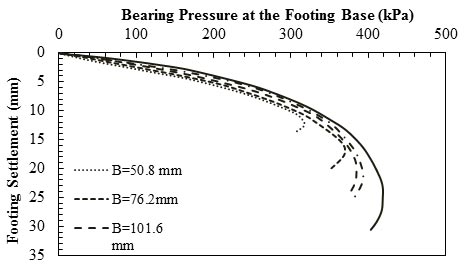
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Das and Omar.(67)

Figure 18. Graph. Load-settlement results in reinforced sand (DR = 75 percent).

Effect of Embedment Depth of Top Reinforcement Layer on Settlement of Shallow Foundations

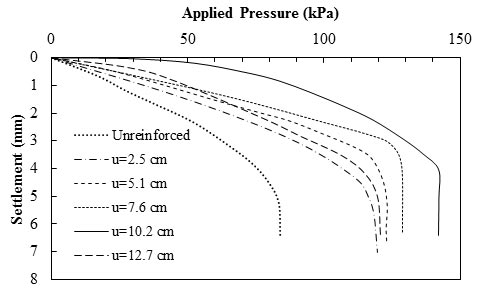
Mandal and Sah conducted bearing capacity tests on model footings on clay subgrades reinforced with geogrids.(68) Their results, plotted in figure 19, show that the maximum percentage reduction in settlement with the use of geogrid reinforcement within the compacted and saturated clay was about 45 percent, and it occurred at a depth of 0 to 0.25B below the base of the square foundation.

 

This graph shows the experimental results for square foundation placed on reinforced clayey soil. The y-axis shows normalized settlement from 0 to 30 percent, and the x-axis shows bearing pressure at footing base from 0 to 250 kPa (where 1 kPa equals 0.145 psi). The plot has six lines that lead from the origin and represent the load-settlement behaviors of foundation placed on unreinforced soil and reinforced soil with different depths of top layer reinforcement: unreinforced and u/B equals 1, 0.75, 0.5, 0.25, and 0, where u/B is the ratio of embedment depth of top geogrid layer to width of foundation. By decreasing the reinforcement spacing from 1 to 0.25, the amount of settlement at each applied pressure decreases. The curve for u/B equal to 0 is placed between the curves for 0.5 and 0.25. For example, at 130 kPa of applied pressure, the settlement of the foundation is about 17 mm for unreinforced soil (where 1 mm equals 0.039 inch) and 14, 12, 10, 8, and 9 mm for reinforced soil with u/B equal to 1, 0.75, 0.5, 0.25, and 0, respectively.
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Mandal and Sah.(68)

Figure 19. Graph. Load-settlement results of model footings on clay subgrade reinforced with geogrid.

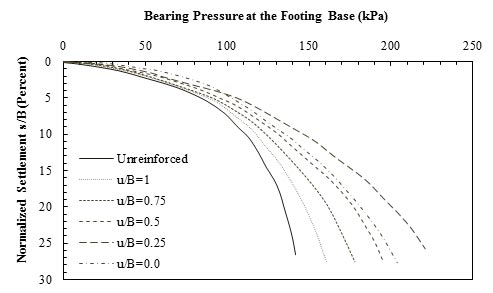
Binquet and Lee conducted a series of experiments on strip footing 2.99 inches (76 mm) wide placed on sandy soil reinforced with metal strips.(69) Figure 20 shows the results of the studies on the effect of u of the top reinforcement layer on the settlement of a foundation. They concluded that the optimum location of the top layer was at u/B = 1.3. Furthermore, based on experimental results obtained from foundations placed on reinforced soil with geogrid, it was concluded that the optimum depth for placing the top layer of reinforcement was within 0.25B below the base of the foundation. Therefore, the top layer of the metal strip could be located at a lower depth compared to geogrid reinforcement in order to have the minimum amount of settlement under each applied load.

This graph shows the experimental results for different depth of top layer of metallic reinforcement with three layers of reinforcement. The y-axis shows settlement from 0 to 8 mm, and the x-axis shows applied pressure at footing base from 0 to 150 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has six lines that lead from the origin and represent the load-settlement behavior of foundation placed on unreinforced soil and reinforced soil with different depths of top layer of reinforcement: unreinforced and u equals 2.5, 5.1, 7.6, 10.2, and 12.7 cm (where 1 cm equals 0.39 inch), where u is the embedment depth of top geogrid layer. By increasing the embedment depth from 2.5 to 10.2 cm, the amount of settlement at each applied pressure decreases, while increasing the depth to 12.7 cm increases the settlement. The curve for u equals 12.7 cm is placed between u equals 2.5 cm and u equals 5.1 curves. For all of the cases, the rate of change in bearing capacity decreases with increasing the settlement until the bearing capacity reaches a plateau. The ultimate pressure is about 85 kPa for unreinforced soil and 118, 125, 130, 142, and 120 kPa for reinforced soil with embedment depths of 2.5, 5.1, 7.6, 10.2, and 12.7 cm, respectively. The settlement at ultimate load remains practically constant between 4 and 6 mm.
1 inch = 25.4 mm = 2.54 cm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Binquet and Lee.(69)

Figure 20. Graph. Load-settlement results for different depth of top layer of metallic reinforcement (N = 3).

Effect of Vertical Spacing of Reinforcement (Sv) Layers on Settlement of Shallow Foundations

Chen et al. investigated the behavior of square foundations on geosynthetic reinforced clayey soil of low to medium plasticity using laboratory model footing tests.(56) As figure 21 shows, by decreasing h between the three reinforcement layers (placed within the zone of influence below the footing), the amount of settlement at each applied load pressure decreased.

This graph shows the experimental results for square foundation placed on reinforced clayey soil. The y-axis shows footing settlement from 0 to 45 mm, and the x-axis shows bearing pressure at footing base from 0 to 2,000 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has five curved lines that lead from the origin and represent the load-settlement behavior of foundation placed on unreinforced soil and reinforced soil with reinforcement spacings of 102, 76, 51, and 25 mm, respectively, with three layers of reinforcement. For all the cases, the rate of change in bearing capacity decreases with increasing the settlement until the first 5 to 10 mm settlement. After that, they have an almost linear slope. The final bearing pressures are 850, 1,330, 1,420, 1,425, and 1,610 kPa at about 40 mm settlement for the unreinforced soil with reinforcement spacings of 102, 76, 51, and 25 mm, respectively, for the reinforced soils.
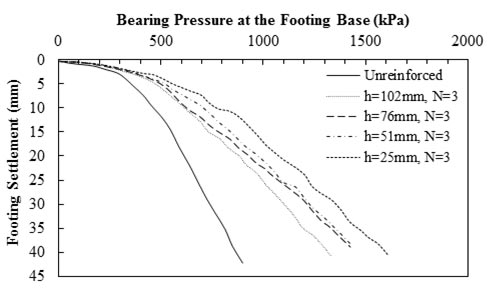
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Chen et al.(56)

Figure 21. Graph. Load-settlement results for square footing tests with three layers of geogrids placed at different vertical spacing.

Effect of Covering Ratio (CR) of Metallic Strip Reinforcement on Settlement of Shallow Foundations

An effective parameter for the load-settlement behavior of foundation on soil reinforced with metallic strips is the CR of reinforcement in each layer. Figure 22 shows the experimental results of the settlement of a foundation placed on reinforced soil with phosphor-bronze strip layers.(60) The figure shows by increasing CR, the settlement at each applied pressure decreases. From the results, it can be concluded that the decrease in settlement was not proportional to CR. This suggests that there is an upper bound in CR, above which a decrease in settlement with the increase in CR may not be expected.

This graph shows the experimental results for different covering ratios (CRs) of reinforcement where L is the length of reinforcement layer) equals 2B (2 times of foundation width and three layers of reinforcement (N). The y-axis shows settlement from 0 to 16 mm, and the x-axis shows applied pressure from 0 to 250 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has four curved lines leading from the origin to their ultimate pressure: unreinforced, CR of 4.5 percent, CR of 9 percent, and CR of 18 percent. The ultimate pressure of the foundation is 95 kPa for the unreinforced soil and 130, 175, and 220 kPa for the reinforced soil with covering ratios of 4.5, 9, and 18 percent, respectively. The corresponding settlements for these pressures are 7, 9, 10, and 11 mm, respectively.
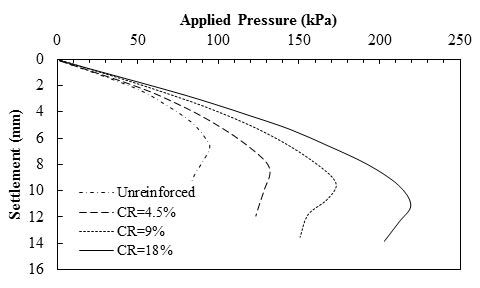
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Huang and Tatsuoka.(60)

Figure 22. Graph. Load-settlement results for different CRs of reinforcement (L = 2B, N = 3).

 

3.3 Synthesis of Load Deformation Relationships of Bridge Abutments and Piers

Effect of Soil Parameters on Load Deformation Relationships

Adams and Nicks conducted an experimental study to investigate secondary deformation characteristics of GRS as bridge piers under service load conditions.(27) Load-settlement behaviors of four GRS piers built using two types of soils and woven geotextiles were monitored under 30.45 psi (210 kPa) of pressure. The characteristics of the materials used and results presented by Adams and Nicks are shown in table 9.(27) The results show that under service load conditions, there was no significant increase in settlement for the pier with the weak geotextile (pier A). Also, the piers with open-graded #8 aggregates experienced slightly more compression (about 5 percent higher) compared to well-graded A-1-a backfill soil. The results from the pier deformation survey over 4 mo indicated that secondary settlement occurred in granular material, but it was still within typical tolerable limits for bridges of up to 2 percent vertical strain over the life of the bridge.(32)

Table 9. GRS pier materials and results recorded from vertical deformation survey.
Measurement Categories Material Properties and Specific Field Surveys Pier A Pier B Pier C Pier D
Backfill material properties AASHTO soil type #8 A-1-a A-1-a #8
Φ (degrees) 55 54 54 55
c (kPa) 0 5.5 5.5 0
Reinforcement properties Tf (kN/m) 35 70 70 70
Minimum average roll value strength at 2 percent strain (kN/m) 3.5 19.3 19.3 19.3
Survey results GRS composite settlement 105 days after load placement (mm) 24 23.6 22.5 24.8
Vertical strain in GRS composite (percent) 1.03 1.01 0.97 1.07
1 psi = 6.89 kPa
1kN/m = 68.5 lbf/ft
1 inch = 25.4 mm
Note: This table was created by FHWA after Adams and Nicks.(27)

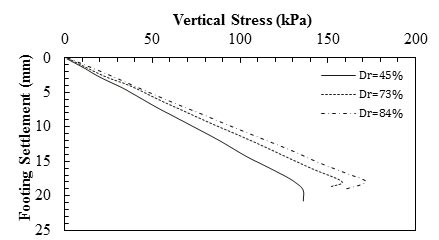
Nicks et al. conducted 19 GRS PTs as a part of FHWA research that investigated axial load versus vertical deformation characteristics of GRS piers.(42) A total of 5 tests were conducted at the Defiance County (DC), OH, highway maintenance facility, and 14 were conducted at the Turner-Fairbank Highway Research Center (TFHRC). The parameters that varied among tests were reinforcement spacing, geotextile strength, soil type, and frictionally connected facing element. The parameters of piers tested to investigate the effect of aggregate type on load- deformation characteristics of the piers and the test results are shown in table 10 and figure 23. The applied pressure was calculated as the average of the measured values over the period of loading, and the vertical strain was calculated as the averages of the four linear voltage displacement transducers (LVDTs) and potentiometers (POTs) located on the footing at the end of each load increment. Based on the results, the pier built with the largest aggregate tested (#57 stone) had the lowest service limit of all the tests, indicating more deformation under an applied load. In addition, the pier built with rounded pea gravel had a lower strength and service limit than the more angular aggregate meeting the same gradation specifications for an AASHTO #8 material.

Table 10. Parametric study on aggregate size.
Test No. Backfill Reinforcement Facing
Type Φ
(degree)		 c
(kPa)		 Aggregate
Size
(mm)		 Tf
(kN/m)		 Sv
(mm)
DC-1 8 54 0 12.7 70 194 CMU
DC-2 8P 46 0 19.05 70 194 CMU
DC-3 57 52 0 25.4 70 194 CMU
DC-4 9 49 0 9.525 70 194 CMU
1 psi = 6.89 kPa
1kN/m = 68.5 lbf/ft
1 inch = 25.4 mm
CMU = Concrete Masonry Unit.
Note: This table was created by FHWA after Nicks et al.(42)

 

This graph shows the load deformation behavior from performance tests (PTs) on geosynthetic reinforced soil (GRS) piers using five types of Defiance County (DC), OH, backfills. The y-axis shows vertical strain from 0 to 9 percent, and the x-axis shows applied pressure from 0 to 1,400 kPa (where 1 kPa equals 0.145 psi). The plot has four lines leading from the origin to a specific point labeled DC 1 through 4. The slope of the DC-1 line is almost the mildest one until 1,000 kPa. The DC-2 and DC-4 lines have the same slope, and the slope of DC-3 line is steeper than others.
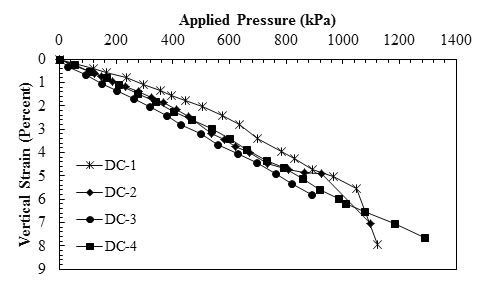
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Nicks et al.(42)

Figure 23. Graph. Load-deformation behavior from PTs on GRS piers using five types of DC backfills.

By comparing identical piers that were similar in all of their characteristics except their gradation, Nicks et al. concluded that the use of well-graded material resulted in a considerably stiffer load-deformation response than that observed when open-graded material was used.(42)

Helwany et al. conducted finite element analyses (FEAs) of two full-scale loading tests on GRS bridge abutments and performed a parametric study to investigate the performance of the modular block facing of GRS bridge abutments subjected to live and dead loads from the bridge superstructure.(70) They concluded that more favorable deformation response was attained when using soil types that have higher internal Φ and corresponding higher bulk and shear moduli. figure 24 shows that when Φ increased from 34 to 40 degrees, the vertical displacement at the abutment seat decreased from 1.89 to 1.18 inches (48 to 30 mm) at applied pressure of 4,177 psf (200 kPa), while vertical displacement showed little variation at a lower applied pressure of 2,088 psf (100 kPa).

This graph shows the effects of backfill internal friction angle (Φ) on vertical displacement at the abutment seat with a reinforcement spacing of 7.87 inches (20 cm). The y-axis shows vertical displacement from 0 to 15 cm (where 1 cm equals 0.39 inch), and the x-axis shows the backfill internal Φ from 34 to 40 degrees. The plot has three lines representing the results under three different applied pressures: 100, 200, and 400 kPa (where 1 kPa equals 0.145 psi). The vertical displacement at seat changes linearly from 1.9 cm at 34 degrees to 1.4 cm at 40 degrees under 100 kPa. At 200 kPa, the vertical displacement decreases linearly from 4.6 cm at 34 degrees to 3.1 cm at 40 degrees. At 400 kPa, the vertical displacement decreases linearly from 10.3 cm at 34 degrees to 6.6 cm at 40 degrees.
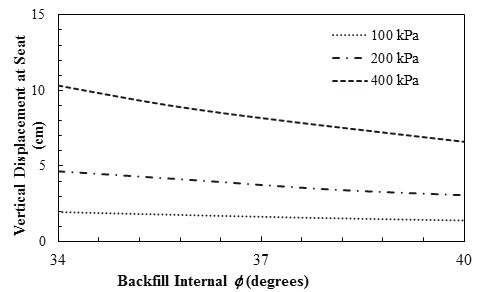
1 inch = 2.54 cm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 24. Graph. Effects of backfill internal Φ on vertical displacement at abutment seat (reinforcement spacing = 7.87 inches (20 cm))

Helwany et al. also concluded that by using soil types that had higher internal Φ and higher bulk and shear moduli, a more favorable deformation response was attained for horizontal displacement at the abutment seat and for maximum lateral displacement of the segmental facing (see figure 26).(70) At applied pressure of 4,177 psf (200 kPa), by increasing the internal Φ from 34 to 40 degrees, the horizontal displacement at seat decreased by about 14 percent. As figure 26 shows, at different applied pressures, the maximum lateral displacement of the segmental facing decreased in a linear manner with increasing Φ .

This graph shows the effects of backfill internal friction angle (Φ) with a reinforcement spacing of 7.87 inches (20 cm) on horizontal displacement at the abutment seat. The y-axis shows horizontal displacement at seat from 0 to 60 mm (where 1 mm equals 0.039 inch), and the x-axis shows backfill internal friction angle from 34 to 40 degrees. The plot has three lines representing the results under three different applied pressures: 100, 200, and 400 kPa (where 1 kPa equals 0.145 psi). The horizontal displacement at seat is almost constant under 100 kPa at 7 mm. At 200 kPa, the horizontal displacement decreases linearly from 21 mm at 34 degrees to 17 mm at 40 degrees. At 400 kPa, the horizontal displacement decreases linearly from 42 mm at 34 degrees to 37 mm at 40 degrees.
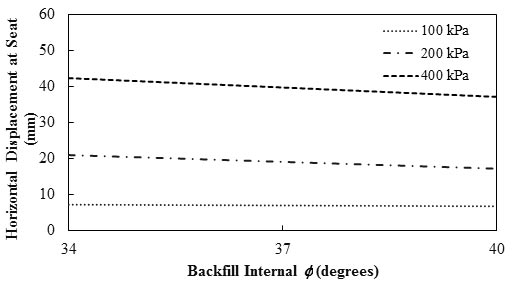
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 25. Graph. Effects of backfill internal Φ (reinforcement spacing = 7.87 inches (20 cm)) on horizontal displacement at abutment seat.

 

This graph shows the effects of backfill internal friction angle (Φ) at a reinforcement spacing of 7.87 inches (20 cm) on the maximum lateral displacement of the facing. The y-axis shows maximum facing displacement from 0 to 15 cm (where 1 cm equals 0.39 inch), and the x-axis shows backfill internal friction angle from 34 to 40 degrees. The plot has four lines representing the results under the abutment self weight and three different applied pressures (100, 200, and 400 kPa) (where 1 kPa equals 0.145 psi). The maximum facing displacement decreases linearly from 3.5 cm at 34 degrees to 1.6 cm at 40 degrees under the abutment self weight. At 100 kPa, the maximum displacement decreases linearly from 4.4 cm at 34 degrees to 2.5 cm at 40 degrees. At 200 kPa, the maximum displacement decreases linearly from 6.0 cm at 34 degrees to 3.3 cm at 40 degrees. At 400 kPa, the horizontal displacement decreases linearly from 9.4 cm at 34 degrees to 5.7 cm at 40 degrees.
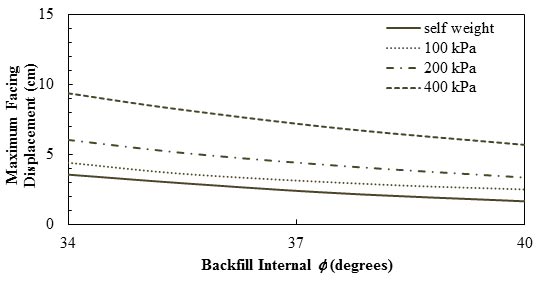
1 inch = 2.54 cm
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 26. Graph. Effects of backfill internal Φ (reinforcement spacing = 7.87 inches (20 cm)) on the maximum lateral displacement of the facing.

Hatami and Bathurst investigated the influence of backfill type on the performance of reinforced soil segmental retaining walls (SRWs) under working stress conditions at the end of construction (EOC) using a finite difference numerical modeling.(71) As figure 27 shows, facing deflections diminished in magnitude as soil shear strength increased due to an increase in Φ, an increase in apparent c, or both. The pattern of deflected shape was also influenced by the increase of apparent c. An increase of apparent c moved the location of maximum wall deflection lower down the wall and was particularly effective in reducing deflections at the wall crest. The results also show the different influences of Φ and c

This graph shows the influence of apparent cohesion (c) and friction angle (Φ) on lateral displacement of the wall. The y-axis shows elevation from 0 to 7 m, and the x-axis shows lateral displacement from 0 to 12 cm (where 1 m equals 3.28 ft, and 1 cm equals 0.39 inch). The plot has four curved lines representing the facing deflection of four retaining walls with different backfill materials: Φ of 30 degrees and c of 10 kPa (where 1 kPa equals 0.145 psi), Φ of 20 degrees and c of 10 kPa, Φ of 40 degrees and c of 1 kPa, and Φ of 30 degrees and c of 1 kPa. The wall with Φ of 30 degrees and c of 10 kPa has the least amount of deflection. Its maximum displacement is 1.2 cm, which occurs at 2.2 m elevation, and the lateral displacement of its top is 0.6 cm. For the wall with Φof 20 degrees and c of 10 kPa, the maximum displacement is 2.7 cm at 2.0 m elevation and 0.7 cm at its top. The maximum lateral displacement of the wall with Φ of 40 degrees and c of 1 kPa is 2.7 cm at 2.0 m elevation and it has 2.8 cm deflection at its top. The wall with Φ of 30 degrees and c of 1 kPa has the most amount of deflection. Its maximum displacement is 8.5 cm, which occurs at 4.2 m elevation, and the lateral displacement of its top is 7.8 cm.
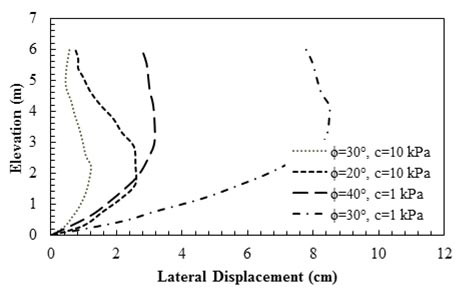
1 ft = 0.305 m
1 inch = 2.54 cm
Note: This figure was created by FHWA after Hatami and Bathurst.(71)

Figure 27. Graph. Influence of apparent c and Φ on lateral displacement of the wall.

Results plotted in figure 28 show that reinforcement loads were greater for the walls with weaker backfills, and the distribution of maximum load along the wall height varied between a parabolic shape for granular backfill and a linear shape when the backfill had higher value of apparent c and was more cohesive.(71)

This graph shows the influence of backfill apparent cohesion (c) and friction angle (Φ) on values on maximum reinforcement loads in wall models at the end of construction (EOC). The y-axis shows elevation from 0 to 7 m, and the x-axis shows load within reinforced soil zone from 0 to 10 kN/m (where 1 m equals 3.28 ft, and 1 kN/m equals 68.5 lbf/ft). The plot has four curved lines representing the results of four retaining walls with different backfill materials: 30-degree Φ with c of 10 kPa (where 1 kPa equals 0.145 psi), 20-degree Φ with c of 10 kPa, 40-degree Φ with c of 1 kPa, and 30-degree with c of 1 kPa. The wall with the 30-degree Φ and c of 10 kPa has the minimum amount of reinforcement load: 1.2 kN/m at the bottom, 0.1 kN/m at the top, and maximum value of 1.4 kN/m at 1.5-m elevation. The reinforcement load for the wall with 20-degree Φ and c of 10 kPa is 2.5 kN/m at the bottom, 0.1 kN/m at top, and maximum value of 2.9 kN/m at 0.9-m elevation. The reinforcement load for the wall with Φ of 40 and c of 11 kPa is 2.1 kN/m at the bottom, 0.5 kN/m at the top, and the maximum value of 3.2 kN/m at 2.1-m elevation. The wall with 30-degree Φ and c of 1 kPa has the maximum amount of reinforcement load, 4.1 kN/m at the bottom, 0.9 kN/m at the top, and the maximum value of 6.8 kN/m at 2.7-m elevation.
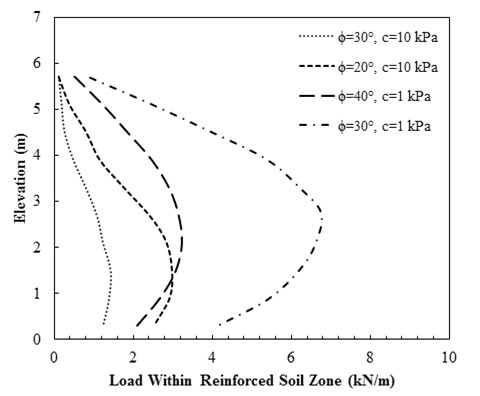
1 ft = 0.305 m
1kN/m = 68.5 lbf/ft
Note: This figure was created by FHWA after Hatami and Bathurst.(71)

Figure 28. Graph. Influence of backfill apparent c and Φ values on maximum reinforcement loads in wall models at EOC

Skinner and Rowe numerically investigated the short- and long-term behaviors of a 19.68-ft (6-m)-high segmental block-faced geosynthetic reinforced retaining wall constructed on a rigid base; they also studied two 32.8-ft (10-m)-thick clayey foundations to investigate the effect of yielding in the foundation on the stability of the wall.(72) The horizontal displacements of the wall face calculated for the rigid foundation and the two clayey foundations are plotted in figure 29. Clayey foundations are significantly more compressible than the rigid foundation. The figure shows that the deformations at the face and base of the wall were considerably higher for soils 1 and 2 than for the rigid foundation. The increased foundation deformation contributed significantly to the facing displacement. For the lower viscosity soil 1, there was no significant change in behavior between the time of 95 percent consolidation (reached 1 year after EOC) and subsequent time (e.g., 7 years). The more viscous soil 2 reached approximately 20 percent consolidation 1 year after EOC and approximately 95 percent consolidation 7 years after EOC. The slight backward rotation of the wall face from EOC to 7 years (95 percent consolidation) for soil 1 was caused by local displacements at the face and especially at the toe of the wall.

This graph shows the horizontal displacements at the wall face. The y-axis shows height above top of foundation from 10 to 16 m, and the x-axis shows horizontal displacement from 0 to 200 mm (where 1 m equals 3.28 ft, and 1 mm equals 0.039 inch). The plot has six curved lines: rigid foundation, soil 1 at end of construction, soil 2 at end of construction, soil 1 after 1 year and 7 years, soil 2 after 1 year, and soil 2 after 7 years. The wall placed on rigid foundation has no displacement at its bottom and top and has 15.4 mm displacement 4.0 m elevation, which is 14 m above top of foundation. At the end of construction, the horizontal displacement of wall placed on soil 1 is 60 mm at 3 m elevation (which is 13 m above top of foundation) and 50 mm at the bottom. After 1 to 7 years, the horizontal displacement of wall placed on soil 1 is 60 mm at 3 m elevation (which is 13 m above top of foundation) and 46 mm at the bottom. At the end of construction, the horizontal displacement of the wall placed on soil 2 is 65 mm from 0 to 3 m elevation (which is 10 to 13 m above top of foundation). Over the time, the horizontal displacement of the wall increases with increasing the depth of the wall, and it has the maximum amount of 94 and 147 mm at its bottom after 1 year and 7 years, respectively.
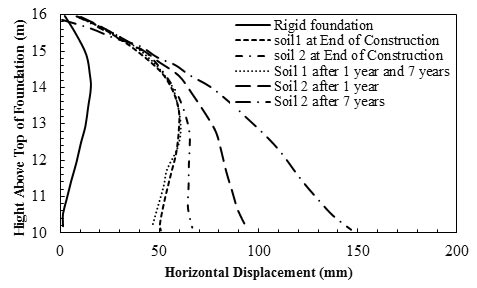
1 ft = 0.305 m
1 inch = 25.4 mm
Note: This figure was created by FHWA after Skinner and Rowe.(72)

Figure 29. Graph. Horizontal displacements at wall face

Helwany et al. conducted FEAs to investigate the effect of backfill type and reinforcement strength on the behavior of GRS retaining walls.(73) A total of 3 different reinforcement stiffness values and 16 different backfill materials were implemented in the analyses of 3 walls with different heights to produce 144 analysis combinations. The GRS retaining walls were under 15.23-psi (105-kPa) surcharge pressure. The dimensions and the properties of the different soils are presented in table 11 and table 12, and the results are plotted in figure 30 through figure 33.

Table 11. GRS retaining wall dimensions.
Wall Height (m) Depth of Backfill (m) Length of Geotextile (m) N
3 3.7 1.8 10
4.5 5.5 2.7 15
6 7.3 3.7 20
1 ft = 0.305 m
Note: This figure was created by FHWA after Helwany et al.(73)

 

Table 12. Representative soil parameters.
Soil Type Based on Unified Soil Classification Backfill Designation Number RC Based on Percent of Standard Proctor Moist Unit Weight
(kN/m3)		 Φ for Confining Pressure =
1 Atmosphere Pressure
(degrees)		 Reduction in Φ for a 10-Fold Increase in Confining Pressure
(degrees)		 c
(kN/m2)
Well-graded gravel, poorly graded gravel, well-graded sand, poorly graded sand 1 105 23.6 42 9 0
2 100 22.8 39 7 0
3 95 22.1 36 5 0
4 90 21.3 33 3 0
Silty sand 5 100 21.3 36 8 0
6 95 20.5 34 6 0
7 90 19.7 32 4 0
8 85 18.9 30 2 0
Silty clayey sand 9 100 21.3 33 0 24
10 95 20.5 33 0 19
11 90 19.7 33 0 14
12 85 18.9 33 0 10
Low plasticity clay 13 100 21.3 30 0 19
14 95 20.5 30 0 14
15 90 19.7 30 0 10
16 85 18.9 30 0 5
1 kN/m3 = 6.37 lbf/ft3
1kN/m2 = 20.89 lb/ft2
Note: This table was created by FHWA after Helwany et al.(73)

 

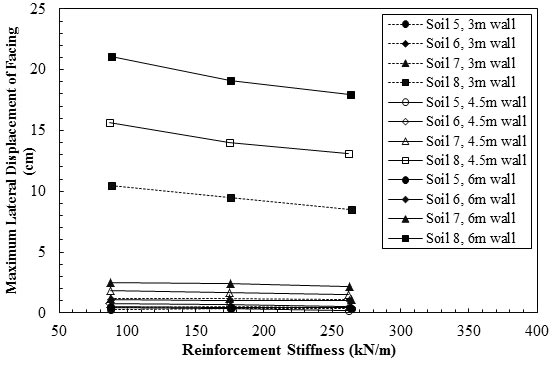
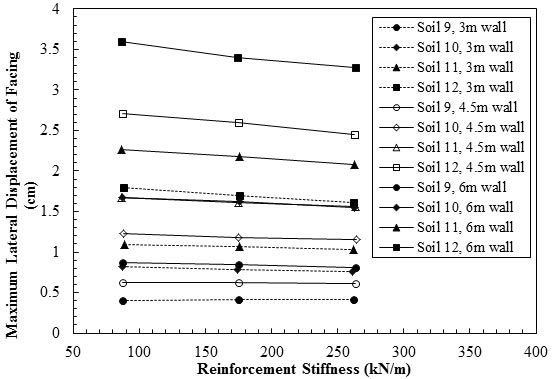
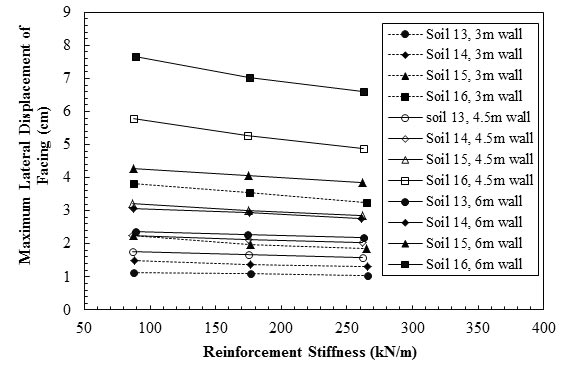
Figure 30 through figure 33 all show that the type of backfill had the most effect on the behavior of the GRS retaining wall. They concluded that the stiffness of the geosynthetic reinforcement had a considerable effect on the behavior of the GRS retaining wall when the backfill was of lower stiffness and shear strength. For example, the 9.84-ft (3-m)-high GRS retaining walls made of soils #15 and #16 (lower stiffness and shear strength) exhibited significant improvement when a stiffer geosynthetic was utilized. When the 9.84-ft (3-m)-high GRS retaining wall was made of soils #13 and #14 (higher stiffness and shear strength), it exhibited relatively small improvements when the geosynthetic stiffness was increased.

This graph shows the maximum lateral displacement versus geosynthetic stiffness for soils 1 through 4. The y-axis shows the maximum lateral displacement of facing from 0 to 6 cm, and the x-axis shows reinforcement stiffness from 0 to 400 kN/m (where 1 cm equals 0.39 inch, and 1 kN/m equals 68.5 lbf/ft). The plot has 12 lines that represent the results of walls with different heights and backfills: soils 1 through 4 with 3-m wall (where 1 m equals 3.28 ft), soils 1 through 4 with 4.5-m wall, and soils 1 through 4 with 6-m wall. The lateral displacements have been reported for reinforcement stiffness of 88, 178, and 265 kN/m. By increasing the reinforcement stiffness from 88 to 265 kN/m, the maximum lateral displacement is almost constant for eight cases (i.e., the walls with backfill of soil 1 and heights of 3, 4.5, and 6 m, the walls with backfill of soil 2 and heights of 3, 4.5, and 6 m, and the walls of backfill of soil 3 and heights of 3 and 4.5 m). For all of these cases, the maximum lateral displacement is less than 1 cm. By increasing the reinforcement stiffness from 88 to 265 kN/m, the maximum lateral displacement decreases linearly from 1.3 to 1.2 cm for the wall with backfill soil 3 and height of 6 m, from 2.4 to 2.1 cm for the wall with backfill soil 4 and height of 3 m, from 3.7 to 3.1 cm for the wall with backfill soil 4 and height of 4.5 m, and from 4.9 to 4.2 cm for the wall with backfill soil 4 and height of 6 m.
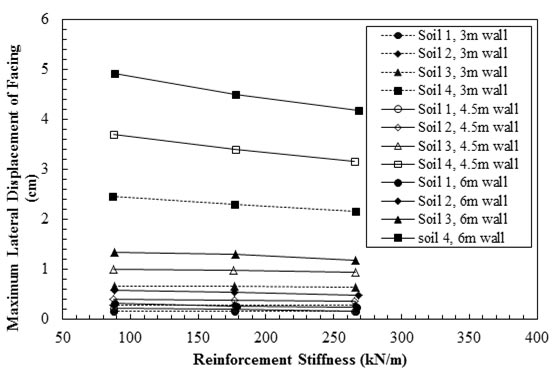
1 inch = 2.54 cm
1 ft = 0.305 m
1kN/m = 68.5 lbf/ft
Note: This figure was created by FHWA after Helwany et al.(73)

Figure 30. Graph. Maximum lateral displacement versus geosynthetic stiffness for soils 1–4.

 

This graph shows the maximum lateral displacement versus geosynthetic stiffness for soils 5 through 8. The y-axis shows the maximum lateral displacement of facing from 0 to 25 cm, and the x-axis shows reinforcement stiffness from 0 to 400 kN/m (where 1 cm equals 0.39 inch, and 1 kN/m equals 68.5 lbf/ft). The plot has 12 lines that represent the results of walls with different heights and backfills: soils 5 through 8 with 3-m wall (where 1 m equals 3.28 ft), soils 5 through 8 with 4.5-m wall, and soils 5 through 8 with 6-m wall. The lateral displacements were reported for reinforcement stiffness of 88, 178, and 265 kN/m. By increasing the reinforcement stiffness from 88 to 265 kN/m, the maximum lateral displacement is almost constant for nine cases (i.e., the walls with backfill of soil 5 and heights of 3, 4.5, and 6 m, the walls with backfill of soil 6 and heights of 3, 4.5, 6 m, and the walls of backfill of soil 7 and heights of 3, 4.5, and 6 m). For all of these cases, the maximum lateral displacement is less than 2.5 cm. By increasing the reinforcement stiffness from 88 to 265 kN/m, the maximum lateral displacement decreases linearly from 10.5 to 8.5 cm for the wall with backfill soil 8 and height of 3 m, from 15.6 to 13.1 cm for the wall with backfill soil 8 and height of 4.5 m, and from 21.1 to 17.9 cm for the wall with backfill soil 8 and height of 6 m.
1 inch = 2.54 cm
1 ft = 0.305 m
1kN/m = 68.5 lbf/ft
Note: This figure was created by FHWA after Helwany et al.(73)

Figure 31. Graph. Maximum lateral displacement versus geosynthetic stiffness for soils 5–8.

 

This graph shows the maximum lateral displacement versus geosynthetic stiffness for soils 9 through 12. The y-axis shows the maximum lateral displacement of facing from 0 to 4 cm, and the x-axis shows reinforcement stiffness from 0 to 400 kN/m (where 1 cm equals 0.39 inch, and 1 kN/m equals 68.5 lbf/ft). The plot has 12 lines that represent the results of walls with different heights and backfills: soils 9 through 12 with 3-m wall (where 1 m equals 3.28 ft), soils 9 through 12 with 4.5-m wall, and soils 9 through 12 with 6-m wall. The lateral displacements have been reported for reinforcement stiffness of 88, 178, and 265 kN/m. By increasing the reinforcement stiffness from 88 to 265 kN/m, the maximum lateral displacement is almost constant for six cases (i.e., the walls with backfill of soil 9 and heights of 3, 4.5, and 6 m, the walls with backfill of soil 10 and heights of 3 and 4.5 m, and the walls of backfill of soil 11 and height of 3 m). For all of these cases, the maximum lateral displacement is less than 1.2 cm. By increasing the reinforcement stiffness from 88 to 265 kN/m, the maximum lateral displacement decreases linearly from 1.7 to 1.5 cm for the walls with backfill soil 10 and height of 6 m and backfill soil 11 and height of 4.5 m, from 1.8 to 1.6 cm for the wall with backfill soil 12 and height of 3 m, from 2.3 to 2.1 cm for the wall with backfill soil 11 and height of 6 m, from 2.7 to 2.4 cm for the wall with backfill soil 12 and height of 4.5 m, and from 3.6 to 3.3 cm for the wall with backfill soil 12 and height of 6 m.
1 inch = 2.54 cm
1 ft = 0.305 m
1kN/m = 68.5 lbf/ft
Note: This figure was created by FHWA after Helwany et al.(73)

Figure 32. Graph. Maximum lateral displacement versus geosynthetic stiffness for soils 9–12.

 

This graph shows the maximum lateral displacement versus geosynthetic stiffness for soils 13 through 16. The y-axis shows maximum lateral displacement of facing from 0 to 9 cm, and the x-axis shows reinforcement stiffness from 0 to 400 kN/m (where 1 cm equals 0.39 inch, and 1 kN/m equals 68.5 lbf/ft). The plot has 12 lines that represent the results of walls with different heights and backfills: soils 13 through 16 with 3-m wall (where 1 m equals 3.28 ft), soils 13 through 16 with 4.5-m wall, and soils 13 through 16 with 6-m wall. The lateral displacements have been reported for reinforcement stiffness of 88, 178, and 265 kN/m. By increasing the reinforcement stiffness from 88 to 265 kN/m, the maximum lateral displacement is almost constant for six cases (i.e., the walls with backfill of soil 13 and heights of 3, 4.5, and 6m, the walls with backfill of soil 14 and heights of and 4.5 m, and the wall of backfill of soil 15 and height of 3 m). For all of these cases, the maximum lateral displacement is less than 2.5 cm. By increasing the reinforcement stiffness from 88 to 265 kN/m, the maximum lateral displacement decreases linearly from 3.1 to 2.6 cm for the wall with backfill soil 14 and height of 6 m, from 3.2 to 2.7 cm for the wall with backfill soil 15 and height of 4.5 m, from 3.8 to 3.2 cm for the wall with backfill soil 16 and height of 3 m, from 4.3 to 3.8 cm for the wall with backfill soil 15 and height of 6 m, from 5.8 to 4.9 cm for the wall with backfill soil 16 and height of 4.5 m, and from 7.7 to 6.6 cm for the wall with backfill soil 16 and height of 3 m.
1 inch = 2.54 cm
1 ft = 0.305 m
1kN/m = 68.5 lbf/ft
Note: This figure was created by FHWA after Helwany et al.(73)

Figure 33. Graph. Maximum lateral displacement versus geosynthetic stiffness for soils 13–16.

 

Effect of Reinforcement Characteristics on Load Deformation Relationships

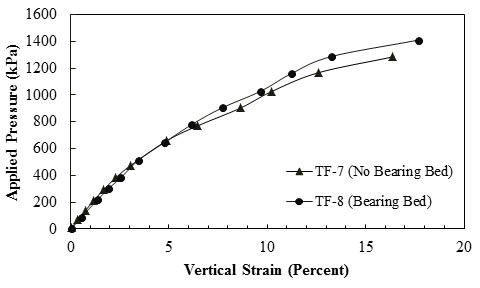
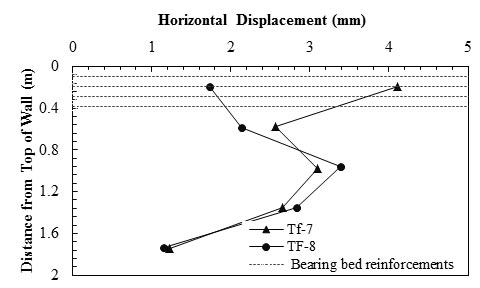
Figure 34 and figure 35 show the results from two PTs conducted by Nicks et al. to investigate the effect of bearing bed reinforcement on load deformation characteristics of bridge piers.(42) Bearing bed reinforcement placed directly underneath the beam seat was recommended in at least the top five courses of CMU facing elements for GRS abutments to support the increased loads due to the bridge and should be, at a minimum, half the primary spacing.(32) The two piers were identical except one pier (Turner-Fairbank (TF)-8) had two courses of bearing bed reinforcement in addition to the primary reinforcement of 7.87-inch (20-cm) spacing, and the other pier (TF-7) had no bearing bed reinforcement with only primary reinforcement. The applied pressure was calculated as the average of the measured values over the period of loading, and the vertical strain was calculated as the averages of the four LVDTs and POTs located on the footing at the end of each load increment. The axial deformations plotted in figure 34 indicate that the bearing bed provided marginally higher vertical capacity; however, vertical deformation was not improved at low strain levels. Figure 35 shows that at service loads (3,550-psf (170-kPa) applied vertical pressure), the lateral deformation of the top 1.31-ft (0.4-m)-thick bearing bed reduced by more than 50 percent due to inclusion of two courses of reinforcement.

This graph shows the effect of bearing bed reinforcement for Turner-Fairbank (TF)-7 and TF-8. The y-axis shows applied pressure from 0 to 1,600 kPa (where 1 kPa equals 0.145 psi), and the x-axis shows vertical strain from 0 to 20 percent. The plot has two curved lines that lead from the origin to a specific point. TF-7 pier with no bearing bed is extended to 1,285 kPa at 16.4 percent strain, and TF-8 pier with bearing bed is extended to 1,410 kPa at 17.7 percent strain. They have the same slope until 6 percent vertical strain. After that, the TF-7 pier becomes less steep.
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Nicks et al.(42)

Figure 34. Graph. Effect of bearing bed reinforcement for TF-7 and TF-8.

 

This graph shows the measured lateral deformation at 3,600 psf (172.5 kPa) applied pressure for Turner-Fairbank (TF)-7 with no bearing bed reinforcement and TF-8 with two courses of bearing bed reinforcement. The y-axis shows the distance from the top of wall from 0 to 2 m, and the x-axis shows horizontal displacement from 0 to 5 mm (where 1 m equals 3.28 ft, and 1 mm equals 0.039 inch). The plot has two sets of lines to illustrate the behavior of TF-7 and TF-8 piers. The horizontal displacements of TF-7 pier are 1.2, 3.1, and 4.1 mm corresponding to 1.7, 1.0, and 0.2 m from the top of the wall, respectively. For TF-8 pier, the horizontal displacements are 1.1, 3.4, and 1.7 mm corresponding to 1.7, 1.0, and 0.2 m from the top of the wall, respectively.
1 ft = 0.305 m
1 inch = 25.4 mm
Note: This figure was created by FHWA after Nicks et al.(42)

Figure 35. Graph. Measured lateral deformation at 3,600 psf (172.5 kPa) applied pressure for TF-7 (no bearing bed reinforcement) and TF-8 (two courses of bearing bed reinforcement).

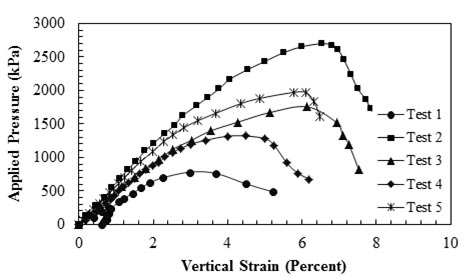
Wu et al. conducted a series of generic soil geosynthetic composite (GSGC) laboratory tests to investigate the composite behavior of GRS mass with varying spacing and Tf of reinforcement.(74) The test program comprised five GSGC tests. The specimen height was 6.56 ft (2 m) with a square cross section of 4.59 ft (1.4 m). The test conditions and a summary of the results are presented in table 13. The vertical movement was measured along the top surface of the concrete pad placed on top of the specimen before loading. Test 1 was conducted as a baseline for the other four tests. The specimen was loaded to 36.26 psi (250 kPa) (nearly up to 1 percent vertical strain), then unloaded to 0 psi (0 kPa) load and reloaded until failure. Other tests were loaded to the failure directly. A prescribed confining pressure of 4.93 psi (34 kPa) was applied on the entire surface area of the test specimens for tests 1 through 4. Figure 36 shows the load deformation behavior of the five GSGC tests. By comparing the results from tests 2 and 3, it can be concluded that the ultimate applied pressure increased by about 35 percent by doubling the reinforcement strength. By comparing tests 2 and 4, it can be concluded that by changing the reinforcement spacing from 1.31 to 0.66 ft (0.4 m to 0.2 m), the ultimate applied pressure increased by more than 50 percent. Therefore, compared to the Tf of reinforcement, the spacing of the reinforcement layers plays a more significant role in improving load-settlement behavior of a reinforced soil mass. Figure 37 shows lateral displacement of the test specimens at failure and at applied pressure of 87.02 psi (600 kPa). Test 2, which was a confined specimen with 0.66-ft (0.2-m) reinforcement spacing, demonstrated the highest ultimate capacity and least lateral deformation.

Table 13. Test conditions and results summary of GSGC tests.
Parameters Test 1 Test 2 Test 3 Test 4 Test 5
Wide-width tensile ultimate strength (kN/m) No reinforcement 70 140 70 70
Reinforcement spacing (m) No reinforcement 0.2 0.4 0.4 0.2
Confining pressure (kPa) 34 34 34 34 0
Ultimate applied pressure (kPa) 770 2,700 1,750 1,300 1,900
Vertical strain at failure (percent) 3 6.5 6.1 4 6
Maximum lateral displacement at failure (mm) 47 60 54 53 Not measured
1 kN/m = 68.5 lbf/ft
1 ft = 0.305 m
1 psi = 6.89 kPa
1 inch = 25.4 mm
Note: This table was created by FHWA adopted from Wu et al.(74)

 

This graph shows the load deformation behaviors for generic soil geosynthetic composite (GSGC) tests. The y-axis shows applied pressure from 0 to 3,000 kPa (where 1 kPa equals 0.145 psi), and the x-axis shows vertical strain from 0 to 10 percent. The plot has five curved lines labeled test 1 through 5 that represent results of five GSGC tests which lead from origin to their peak strength and then lose some strength. The peak strengths are 780, 1,280, 1,755, 1,675, and 1,975 kPa for tests 1 through 5, respectively. The corresponding vertical strains for these peak strengths are 3.0, 4.5, 6.1, 6.8, and 6.1 percent, respectively.
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Wu et al.(74)

Figure 36. Graph. Load-deformation behaviors for GSGC tests.

 

This graph shows the lateral deformation of test specimens at 12,531 psf (600 kPa) and the ultimate applied pressure. The y-axis shows height from 0 to 1.8 m, and the x-axis shows lateral displacement from 0 to 100 mm (where 1 m equals 3.28 ft, and 1 mm equals 0.039 inch). The plot has 10 curved lines that represent the results of five generic soil geosynthetic composite (GSGC) tests at 600 kPa (where 1 kPa equals 0.145 psi) and the ultimate applied pressure. At 600 kPa of applied pressure, the maximum lateral displacements of the specimens are 18.8, 3.7, 8.2, 8.1, and 8.4 mm for tests 1 through 5, respectively. For test 1 at 770 kPa of applied pressure, the lateral displacements are 39.5 mm at a height of 0.5 m, 24.4 mm at the top, and the maximum value of 46.2 mm at a height of 0.7 m. For test 2 at 2,700 kPa of applied pressure, the lateral displacements are 43.1 mm at a height of 0.5 m, 35.3 mm at the top, and the maximum value of 61.5 mm at a height of 1.0 m. For test 3 at 1,750 kPa of applied pressure, the lateral displacements are 44.2 mm at a height of 0.5 m, 37.7 mm at the top, and the maximum value of 53.4 mm at a height of 1.0 m. For test 4 at 1,300 kPa of applied pressure, the lateral displacements are 42.2 mm at a height of 0.5 m, 32.1 mm at the top, and the maximum value of 52.2 mm at a height of 0.7 m. For test 5 at 1,500 kPa of applied pressure, the lateral displacements are 26.2 mm at a height of 0.3 m, 15.7 mm at the top, and the maximum value of 37.1 mm at a height of 1.0 m.
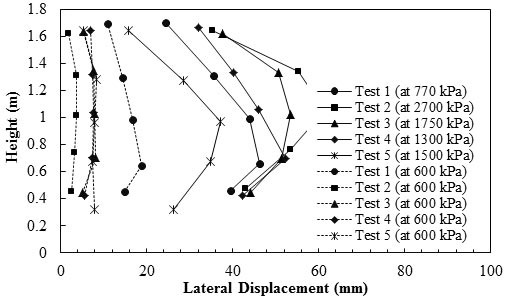
1 ft = 0.305 m
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Wu et al.(74)

Figure 37. Graph. Lateral deformation of test specimens at 12,531 psf (600 kPa) and the ultimate applied pressure.

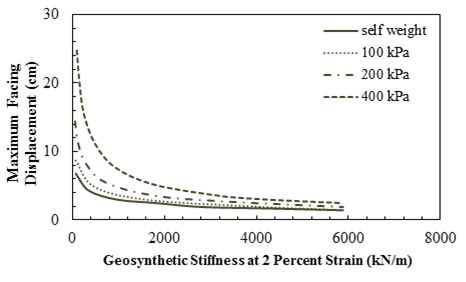
Helwany et al. conducted FEAs to investigate the effects of geosynthetic stiffness on the performance of GRS abutment.(70) The stiffness of the base case was assumed to be 36,305 lbf/ft (530 kN/m). Results plotted in figure 38 show that the vertical displacement of the abutment seat for the base case (for an applied pressure of 4,177 psf (200 kPa)) was reduced by 43 percent when the geosynthetic stiffness increased by 10 times to 363,050 lbf/ft (5,300 kN/m). Conversely, a drastic increase of 250 percent in displacement was noted when the geosynthetic stiffness was reduced to 3,603.5 lbf/ft (53 kN/m). Vertical displacement at the abutment seat increased drastically when axial stiffness of the geosynthetic dropped below a critical value, and the trend became more pronounced with an increase in applied pressure.

This graph shows the effect of geosynthetic stiffness with reinforcement spacing of 7.87 inches (20 cm) on vertical displacement at the abutment seat. The y-axis shows vertical displacement at seat from 0 to 30 cm, and the x-axis shows geosynthetic stiffness at 2 percent strain from 0 to 6,000 kN/m (where 1 cm equals 0.39 inch, and 1 kN/m equals 68.5 lbf/ft). The plot has three lines representing the results under three different applied pressures: 100, 200, and 400 kPa (where 1 kPa equals 0.145 psi). The rate of change in vertical displacement decreases sharply with increasing the geosynthetic stiffness until it reaches a specific stiffness which is about 1,000, 1,800, and 2,300 kN/m for applied pressure of 100, 200, and 400 kPa, respectively. After that, the vertical displacement slightly decreases by increasing the geosynthetic stiffness to 6,000 kN/m. The vertical displacement at 100 kPa decreases from 3.1 to 1.7 cm by increasing the geosynthetic stiffness from 130 to 1,200 kN/m and then decreases to 1.2 cm at 6,000 kN/m of stiffness. At 200 kPa, the vertical displacement decreases from 10.5 to 3.7 cm by increasing the geosynthetic stiffness from 140 to 1,800 kN/m and then decreases to 2.4 cm at 6000 kN/m of stiffness. At 400 kPa, the vertical displacement decreases from 24.1 to 7.1 cm by increasing the geosynthetic stiffness from 170 to 2,300 kN/m and then decreases to 5.0 cm at 6,000 kN/m of stiffness.
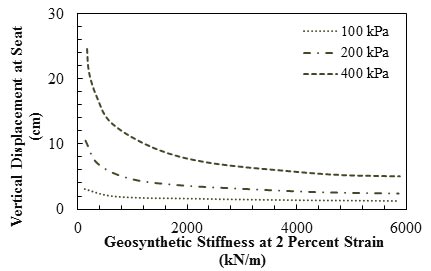
1 inch = 2.54 cm
1 psi = 6.89 kPa
1 kN/m = 68.5 lbf/ft
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 38. Graph. Effect of geosynthetic stiffness (reinforcement spacing = 7.87 inches (20 cm)) on vertical displacement at abutment seat.

Helwany et al. concluded that the vertical displacement at the abutment seat increased when the vertical spacing between reinforcements increased at a high pressure of 58 psi (400 kPa).(70) Figure 39 shows that the increase in vertical displacement became more significant as the applied pressure increased. At an applied pressure of 4,177 psf (200 kPa), an increase of 40 percent in the vertical displacement was observed when the reinforcement vertical spacing increased from 7.87 to 23.62 inches (20 to 60 cm).

This graph shows the effect of geosynthetic spacing on vertical displacement at the abutment seat. The y-axis shows vertical displacement at seat from 0 to 20 cm, and the x-axis shows reinforcement vertical spacing from 20 to 60 cm (where 1 cm equals 0.39 inch). The plot has three lines representing the results under three different applied pressures: 100, 200, and 400 kPa (where 1 kPa equals 0.145 psi). The vertical displacement at seat increases linearly from 1.9 to 2.4 cm for 100 kPa of applied pressure, from 4.9 to 6.9 cm for 200 kPa of applied pressure, and from 10.3 to 16.3 cm for 400 kPa of applied pressure when the reinforcement spacing increases from 20 to 60 cm.
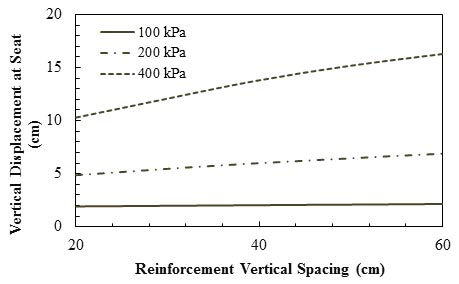
1 inch = 2.54 cm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 39. Graph. Effect of geosynthetic spacing on vertical displacement at abutment seat.

Figure 40 and figure 41 show that the horizontal displacements of the abutment seat and the maximum lateral displacement of the segmental wall decreased when the geosynthetic stiffness increased to 363,050 lbf/ft (5,300 kN/m) from the base case. Conversely, a drastic increase in displacements occurred when the geosynthetic stiffness was reduced to 3,630.5 lbf/ft (53 kN/m).

This graph shows the effect of geosynthetic stiffness with a reinforcement spacing of 7.87 inches (20 cm) on horizontal displacement at the abutment seat. The y-axis shows horizontal displacement at seat from 0 to 16 cm, and the x-axis shows geosynthetic stiffness at 2 percent strain from 0 to 6,000 kN/m (where 1 cm equals 0.39 inch, and 1 kN/m equals 68.5 lbf/ft). The plot has three lines representing the results under three different applied pressures: 100, 200, and 400 kPa (where 1 kPa equals 0.145 psi). The rate of change in horizontal displacement decreases sharply with increasing the geosynthetic stiffness until it reaches a specific stiffness which is about 1,000, 1,800, and 2,000 kN/m for applied pressure of 100, 200, and 400 kPa, respectively. After that, the vertical displacement slightly decreases by increasing the geosynthetic stiffness to 6,000 kN/m. The vertical displacement at 100 kPa decreases from 1.0 to 0.5 cm by increasing the geosynthetic stiffness from 140 to 1,000 kN/m and then decreases to 0.3 cm at 6,000 kN/m of stiffness. At 200 kPa, the vertical displacement decreases from 5.5 to 1.3 cm by increasing the geosynthetic stiffness from 150 to 1650 kN/m and then decreases to 0.7 cm at 6,000 kN/m of stiffness. At 400 kPa, the vertical displacement decreases from 14.9 to 2.6 cm by increasing the geosynthetic stiffness from 140 to 2,000 kN/m and then decreases to 1.5 cm at 6,000 kN/m of stiffness.
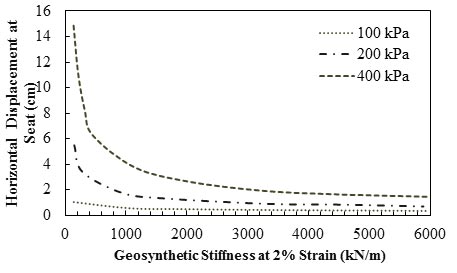
1 inch = 2.54 cm
1 psi = 6.89 kPa
1 kN/m = 68.5 lbf/ft
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 40. Graph. Effect of geosynthetic stiffness (reinforcement spacing = 7.87 inches (20 cm)) on horizontal displacement at abutment seat.

 

This graph shows the effect of geosynthetic stiffness with a reinforcement spacing of 7.87 inches (20 cm) on the maximum lateral displacement of the facing. The y-axis shows maximum facing displacement from 0 to 30 cm, and the x-axis shows geosynthetic stiffness at 2 percent strain in from 0 to 8,000 kN/m (where 1 cm equals 0.39 inch, and 1 kN/m equals 68.5 lbf/ft). The plot has four lines representing the results under the abutment's self weight and three different applied pressures: 100, 200, and 400 kPa (where 1 kPa equals 0.145 psi). The vertical displacement under the abutment self weight decreases from 6.8 to 3.0 cm by increasing the geosynthetic stiffness from 70 to 1,000 kN/m and then decreases to 1.3 cm at 6,000 kN/m of stiffness. At 100 kPa, the vertical displacement decreases from 8.7 to 3.0 cm by increasing the geosynthetic stiffness from 70 to 1,600 kN/m and then decreases to 1.4 cm at 6,000 kN/m of stiffness. At 200 kPa, the vertical displacement decreases from 14.4 to 5.2 cm by increasing the geosynthetic stiffness from 60 to 1,800 kN/m and then decreases to 1.9 cm at 6,000 kN/m of stiffness. At 400 kPa, the vertical displacement decreases from 24.8 to 5.2 cm by increasing the geosynthetic stiffness from 95 to 1,700 kN/m and then decreases to 2.5 cm at 6,000 kN/m of stiffness.
1 inch = 2.54 cm
1 psi = 6.89 kPa
1 kN/m = 68.5 lbf/ft
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 41. Graph. Effect of geosynthetic stiffness (reinforcement spacing = 7.87 inches (20 cm)) on the maximum lateral displacement of the facing.

Based on the FEA of two full-scale loading tests of GRS bridge abutments as well as a parametric study to investigate the performance of GRS bridge abutments, Helwany et al. concluded that the horizontal displacement at the abutment seat and the maximum lateral displacement of the segmental facing increased with an increase in reinforcement spacing (see figure 42 and figure 43).(70) As figure 42 shows, at applied pressure of 29 psi (200 kPa), an increase of 52 percent in the horizontal displacement was observed when reinforcement vertical spacing increased from 7.87 to 23.62 inches (20 to 60 cm). At a lower applied pressure of 14.50 psi (100 kPa), the vertical spacing had a minimum effect on horizontal displacement. As shown in figure 43, at an applied pressure of 29 psi (200 kPa), by increasing the reinforcement spacing from 7.87 to 23.62 inches (20 to 60 cm), the maximum facing displacement increased by about 50 percent.

This graph shows the effect of geosynthetic spacing on horizontal displacement at abutment seat. The y-axis shows horizontal displacement at seat from 0 to 10 cm, and the x-axis shows reinforcement vertical spacing from 20 to 60 cm (where 1 cm equals 0.39 inch). The plot has three lines representing the results under three different applied pressures: 100, 200, and 400 kPa (where 1 kPa equals 0.145 psi). The horizontal displacement at seat is constant at 0.6 cm for different reinforcement spacing under the applied pressure of 100 kPa. The displacement increases linearly from 2.1 to 3.1 cm under 200 kPa of applied pressure and from 4.7 to 7.8 cm under 400 kPa of applied pressure when the reinforcement spacing increases from 20 to 60 cm.
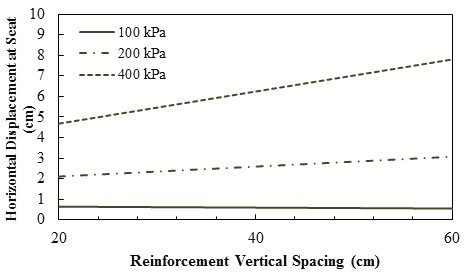
1 inch = 2.54 cm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 42. Graph. Effect of geosynthetic spacing on horizontal displacement at abutment seat.

 

This graph shows the effect of geosynthetic spacing on maximum lateral displacement of the facing. The y-axis shows maximum facing displacement from 0 to 20 cm and the x-axis shows reinforcement vertical spacing from 20 to 60 cm (where 1 cm equals 0.39 inch). The plot has four lines representing the results under the abutment's self weight and three different applied pressures: 100, 200, and 400 kPa (where 1 kPa equals 0.145 psi). The maximum facing displacement increases linearly from 3.6 to 5.4 cm under the self weight of the abutment, from 4.4 to 6.2 cm under 100 kPa of applied pressure, from 6.1 to 9.5 cm under 200 kPa of applied pressure, and from 9.5 to 16.2 cm under 400 kPa of applied pressure when the reinforcement spacing increases from 20 to 60 cm.
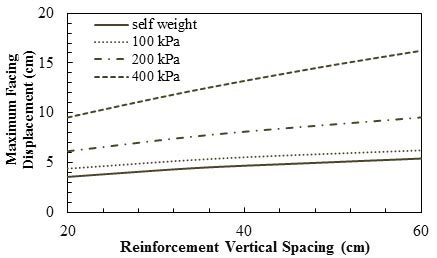
1 inch = 2.54 cm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Helwany et al.(70)

Figure 43. Graph. Effect of geosynthetic spacing on the maximum lateral displacement of the facing.

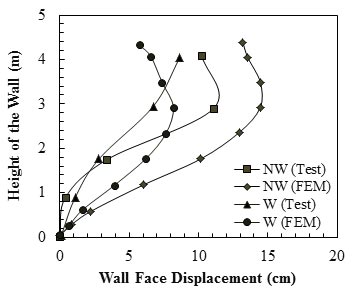
Gotteland et al. performed experimental and numerical studies on two reinforced walls: one was reinforced with a non-woven geotextile (represented by NW) and the other with a woven geotextile (represented by W) (see figure 44 and figure 45).(75) The non-woven geotextile was 3.5 times more extensible than the woven one and approximately half as strong in terms of Tf . After construction, the reinforced walls were loaded in the same way as a bridge deck through a foundation slab until failure occurred. The 3.28-ft (1-m)-wide foundation was located 4.92 ft (1.50 m) from the edge of the facing. As figure 44 shows, the abutment with woven geotextile had a higher ultimate bearing capacity, and its settlement was less compared to the non-woven one. The results in figure 45 show that lateral deformation of the wall face with woven geotextile was less than that with non-woven geotextile.

This graph shows the central settlement of the foundation versus applied load. The y-axis shows settlement from 0 to 35cm, and the x-axis shows applied load from 0 to 300 kN/m (where 1 cm equals 0.39 inch, and 1 kN/m equals 68.5 lbf/ft). The plot has four lines that lead from the origin and represent the load-settlement behavior of two wall reinforced with woven (W) and non-woven (NW) geotextile. For all of the cases, the rate of change in settlement increases with increasing applied load until it reaches a plateau. Based on the test results, the ultimate load is about 230 kN/m for both the NW and W walls, which occurs at 20 to 23 cm of settlement. According to finite element method results, the ultimate load is about 190 kN/m at 25 cm of settlement and 230 kN/m at 18 cm of settlement for NW and W walls, respectively.
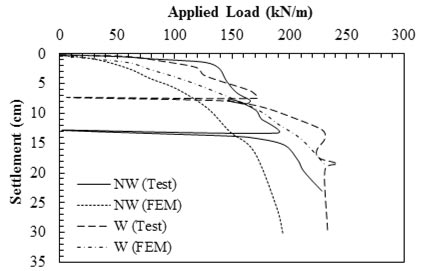
1 inch = 2.54 cm
1 kN/m = 68.5 lbf/ft
FEM = Finite element method.
Note: This figure was created by FHWA after Gotteland et al.(75)

Figure 44. Graph. Central settlement of the foundation versus applied load.

 

This graph shows the wall face displacement at applied pressure of 3,969.1 lb/ft2 (190 kN/m2) for non-woven (NW) and woven (W) reinforcement. The y-axis shows height of the wall from 0 to 5 m, and the x-axis shows wall face displacement from 0 to 20 cm (where 1 m equals 3.28 ft, and 1 cm equals 0.39 inch). The plot has four curved lines that lead from the origin and represent the facing deflection pattern of two reinforced walls based on the test and finite element method (FEM) results. Based on the test results, the maximum face displacement of the NW wall is 11.1 cm at 2.9 m elevation, and it has 10.2 cm deflection at its top. The W wall has the maximum face displacement of 8.6 cm at its top. Based on FEM results, the maximum face displacement of the NW wall is 14.4 cm at 2.9 m elevation, and it has 13.2 cm deflection at its top. The W-wall has the maximum face displacement of 8.2 cm at 2.9 m elevation, and it has 5.7 cm deflection at its top.
1 ft = 0.305 m
1 inch = 2.54 cm
Note: This figure was created by FHWA after Gotteland et al.(75)

Figure 45. Graph. Wall face displacement at applied pressure of 3,969.1 lb/ft2 (190 kN/m2) for non-woven and woven reinforcement

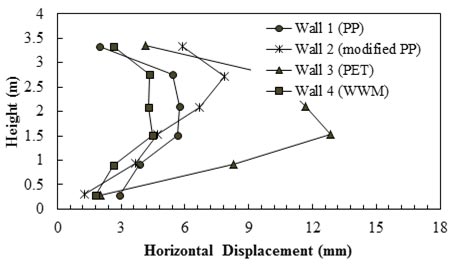
Bathurst et al. conducted experiments on four full-scale modular block walls that were constructed with reinforcement layers with different tensile stiffnesses.(76) The walls were 11.81 ft (3.6 m) high. Two of the walls (walls 1 and 2) were reinforced with two different PP geogrid reinforcements, wall 3 was reinforced with a polyester (PET) geogrid, and wall 4 was reinforced with a welded wire mesh (WWM). Walls 1 and 2 were compacted using vibrating plate equipment, and walls 3 and 4 were compacted by a vibrating rammer. Figure 46 shows measured relative horizontal displacements recorded at monitored points on the wall facing column shortly after EOC. Each elevation point has a local datum corresponding to the time when each row of displacement POTs were installed.

This graph shows the relative horizontal displacement of the wall facing recorded at end of construction (EOC). The y-axis shows height from 0 to 4 m, and the x-axis shows horizontal displacement from 0 to 18 cm (where 1 m equals 3.28 ft, and 1 cm equals 0.39 inch). The plot has four curved lines that represent the horizontal displacement of four walls with different reinforcements (wall 1 polypropylene (PP), wall 2 modified PP, wall 3 polyester (PET), and wall 4 welded wire mesh (WWM). The maximum horizontal displacement of wall 1 (PP) is 5.7 mm (where 1 mm equals 0.039 inch) at 2.1 m elevation and has 1.9 mm deflection at its top and 2.9 mm deflection at its bottom. Wall 2 (modified PP) has the maximum face displacement of 7.9 mm at 2.7 m elevation and has 5.9 mm deflection at its top and 1.2 mm deflection at its bottom. Wall 3 (PET) has the maximum face displacement of 12.9 mm at 1.5 m elevation and has 4.1 mm deflection at its top and 2.0 mm deflection at its bottom. Wall 4 (WWM) has the maximum face displacement of 4.5 mm at 1.5 m elevation and has 2.6 mm deflection at its top and 1.8 mm deflection at its bottom.
1 ft = 0.305 m
1 inch = 25.4 mm
Note: This figure was created by FHWA after Bathurst et al.(76)

Figure 46. Graph. Relative horizontal displacement of wall facing recorded at EOC.

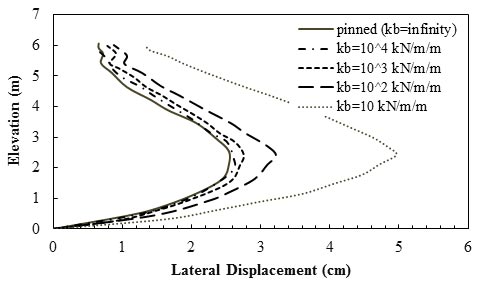
Hatami and Bathurst investigated the influence of reinforcement properties on the performance of reinforced soil SRWs using a finite difference numerical model.(71) They concluded that the deformation response of the model wall with a pinned (fully fixed) reinforcement condition was very close to that of the model with interface stiffness between backfill soil and reinforcement layers (kb) ≥ 145 lbf/inch/inch (1,000 kN/m/m). As figure 47 shows, for values of kb ≤ 145 lbf/inch/inch (1,000 kN/m/m), the lower kb, the greater the wall deformation. The wall deformation magnitude increased by a factor of two when the value of kb was reduced by two orders of magnitude from kb = 145 lbf/inch/inch (103 kN/m/m) to kb = 1.45 lbf/inch/inch (10 kN/m/m).

This graph shows the influence of the soil-reinforcement interface stiffness value on the lateral displacement of the wall. The y-axis shows elevation from 0 to 7 m, and the x-axis shows lateral displacement from 0 to 6 cm (where 1 m equals 3.28 ft, and 1 cm equals 0.39 inch). The plot has five curved lines that lead from the origin and represent the facing deflection pattern of five walls with 6 m height which have different soil-reinforcement interface stiffness. They represent the result of a pinned wall, and walls with interface stiffness equal to 104 kN/m/m, 103 kN/m/m, 102 kN/m/m, and 10 kN/m/m (where 1 kN/m/m equals 0.145 lbf/inch/inch. The maximum lateral displacement of the pinned case (interface stiffness is infinity) is 2.5 cm at 2.6 m elevation, and it has 0.7 cm deflection at its top. The wall with interface stiff ness of 104 kN/m/m has the maximum lateral displacement of 2.6 cm at 1.9 m elevation, and it has 0.7 cm deflection at its top. The wall with interface stiffness of 103 kN/m/m has the maximum lateral displacement of 2.8 cm at 2.4 m elevation, and it has 0.8 cm deflection at its top. The wall with interface stiffness of 102 kN/m/m has the maximum lateral displacement of 3.2 cm at 2.4 m elevation, and it has 0.9 cm deflection at its top. The wall with interface stiffness of 10 kN/m/m has the maximum lateral displacement of 5.0 cm at 2.4 m elevation, and it has 1.4 cm deflection at its top.
1 inch = 2.54 cm
1 kN/m/m = 0.145 lbf/inch/inch
Note: This figure was created by FHWA after Hatami and Bathurst.(71)

Figure 47. Graph. Influence of soil-reinforcement interface stiffness value on lateral displacement of the wall.

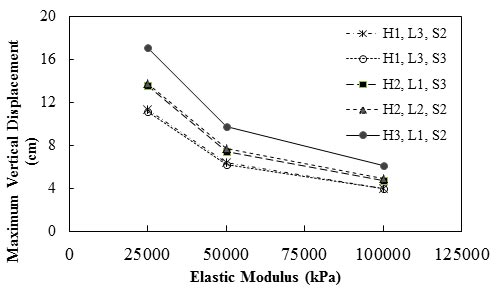
Zevgolis and Bourdeau simulated the performance of MSE abutments with metal strips to investigate the effects of different parameters such as the elastic modulus of reinforcement (ER), H, magnitude of the applied load, and foundation soil type on the behaviors of the abutments.(4) They defined five case studies; H1-L3-S2, H1-L3-S3, H2-L1-S3, H2-L2-S2, and H3-L1-S2, where H1, H2, and H3 stand for the abutments that were 19.66, 22.97, and 26.24 ft (6, 7, and 8 m) tall, respectively; L1, L2, and L3 stand for supported spans that were 59.06, 78.74, and 9,843 ft (18, 24, and 30 m) long with total applied load of 18,152, 22,262, and 26,372 lbf/ft (265, 325, and 385 kN/m), respectively; and S2 and S3 represent different foundation soil types. For S2, Φ was 30 degrees, c was 104 lb/ft2 (5 kPa), and the unit weight was 121 lb/ft3 (19 kN/m3). For S3, Φ was 20 degrees, c was 835 lb/ft2 (40 kPa), and the unit weight was 108 lb/ft3 (17 kN/m3). As figure 48 shows, by increasing Young’s modulus of reinforcement from 3.63 to 7.25 ksi (25 to 50 MPa), the maximum vertical deformation of the abutment decreased at least 42 percent, and by increasing Young’s modulus of reinforcement from 7.25 to 14.50 ksi (50 to 100 MPa), the maximum vertical deformation decreased at least 36 percent. Moreover, the results indicate that higher MSE abutment had more vertical displacement that that of a lower one.

This graph shows the effect of elastic modulus of reinforcement (ER) on the maximum vertical displacement of mechanically stabilized Earth (MSE) abutments with metal strips. The y-axis shows maximum vertical displacement from 0 to 20 cm, and the x-axis shows elastic modulus from 0 to 125,000 kPa (where 1 cm equals 0.39 inch, and 1 kPa equals 0.145 psi). The plot has five lines labeled as H1-L3-S2, H1-L3-S3, H2-L1-S3, H2-L2-S2 and H3-L1-S2 represent different conditions for the MSE abutments. H1, H2, and H3 stand for the abutments that are 19.66, 22.97, and 26.24 ft (6, 7, and 8 m) tall, respectively; L1, L2, and L3 stand for supported spans that are 59.06, 78.74, and 9843 ft (18, 24, and 30 m) long, respectively; and S2 and S3 represent different foundation soil types. For all cases, displacement decreases by increasing the elastic modulus of the reinforcement. The maximum vertical displacements are 11.3, 11.1, 13.6, 13.7, and 17.1 cm for an elastic modulus of 25,000 kPa; 6.4, 6.2, 7.4, 7.7, and 9.8 cm for the elastic modulus of 50,000 kPa; and 4.0, 4.0, 4.7, 4.9, and 6.2 cm for the elastic modulus of 100,000 kPa corresponding to H1-L3-S2, H1-L3-S3, H2-L1-S3, H2-L2-S2, and H3-L1-S2 cases, respectively.
1 inch = 2.54 cm
1 psi = 6.89 kPa

Figure 48. Graph. Effect of ER on the maximum vertical displacement of MSE abutments with metal strips

Tatsuoka et al. and Tateyama performed a series of plane strain model tests of metal strip-reinforced sand retaining walls with three different numbers of reinforcement layers (N = 2, 5, and 10).(77,78) The reinforcement layers were made of phosphor-bronze strips. The model wall was 33.07 inches (84 cm) wide, 15.55 inches (39.5 cm) long, and 20.47 inches (52 cm) tall. As the results plotted in figure 49 show, by increasing N, the vertical displacement of the foundation placed on top of abutment under each applied load decreased. For instance, by increasing N from 2 to 5, the settlement under applied pressure of 1.02 psi (7 kPa) decreased about 70 percent, and by increasing N from 5 to 10, the settlement decreased 53 percent under applied pressure of 2.03 psi (14 kPa). Cao and Peng simulated these experiments through a nonlinear FEM analysis and obtained similar results.(79) The results showed that the peak footing load of reinforced retaining walls increased significantly with an increase in the number of reinforced layers. The experimental results were obtained by Tateyama, and the FEM results were obtained by Cao and Peng.(78,79)

This graph shows the load-settlement results for the foundation on top of mechanically stabilized Earth (MSE) abutment. The y-axis shows footing settlement from 0 to 20 cm, and the x-axis shows average footing pressure from 0 to 50 kPa (where 1 cm equals 0.39 inch, and 1 kPa equals 0.145 psi). The plot has six lines that lead from the origin: experimental result with 2, 5, and 10 layers of reinforcement and finite element method (FEM) result with 2, 5, and 10 layers of reinforcement. Based on the experimental results, the ultimate pressures for 2, 5, and 10 layers of reinforcement are 8 kPa at 5 mm of settlement (where 1 mm equals 0.039 inch), 15 kPa at 7 mm of settlement, and 20 kPa at 6 mm of settlement, respectively. Based on the FEM results, the ultimate pressures for 2, 5, and 10 layers of reinforcement are 8 kPa at 3 mm of settlement, 16 kPa at 4 mm of settlement, and 23 kPa at 4 mm of settlement, respectively.
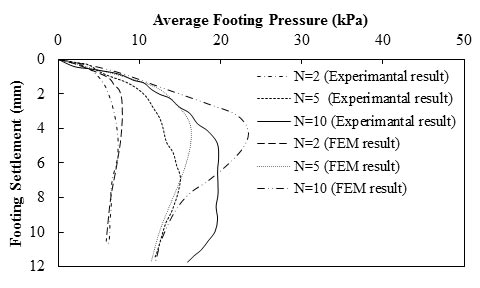
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Zevgolis and Bourdeau.(4)

Figure 49. Graph. Load-settlement results for the foundation on top of MSE abutment.

Effect of Facing Blocks on Load Deformation Relationships

Nicks et al. conducted five pairs of tests as a part of an FHWA research study to investigate the effects of facing elements on load deformation behavior of bridge piers (see figure 50).(42) They concluded that the ultimate capacity of pier increased when a facing element was present; however, the magnitude of strain at failure, which was measured through LVDTs and POTs on the footing, was similar for a given GRS composite with or without a facing.

For figure 50, the following parameters were used:

This graph shows the stress-strain response for different piers. The y-axis shows applied pressure from 0 to 2,500 kPa (where 1 kPa equals 0.145 psi), and the x-axis shows vertical strain from 0 to 25 percent. The plot has 10 curved lines labeled Turner-Fairbank (TF)-2 (with Concrete Masonry Unit (CMU)), TF-3 (No CMU), TF-6 (with CMU), TF-7 (No CMU), TF-9 (with CMU), TF-10 (No CMU), TF-11 (with CMU), TF-12 (No CMU), TF-13 (with CMU) and TF-14 (No CMU). For all of the cases, the rate of change in vertical strain decreases with increasing the applied pressure until it reaches a plateau at approximately 13 to 16 percent strain. The peak strength for different specimens varies between 490 and 2,080 kPa and increases for each pair when a facing element is present.
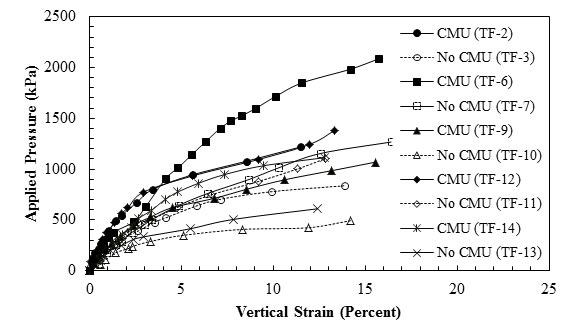
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Nicks et al.(42)

Figure 50. Graph. Stress-strain response for different piers.

Effect of Prestraining on Load Deformation Relationships

A full-scale GRS bridge pier load test was conducted at FHWA’s TFHRC in 1996.(22,23) The GRS pier was prestrained (preloaded) using hydraulic jacks and a specially designed reaction system. Results obtained from this instrumented bridge pier show that the prestraining reduced vertical settlement of the pier by approximately 50 percent (see figure 51). Figure 52 shows that prestraining did not reduce lateral deformation except for near the top of the pier where the lateral movement reduced significantly.

This graph shows the load-settlement curves for the pier. The y-axis shows settlement from 0 to 80 mm, and the x-axis shows applied pressure from 0 to 1,000 kPa (where 1 mm equals 0.039 inch, and 1 kPa equals 0.145 psi). The plot has two lines leading almost linearly from the origin: initial loading and reloading. The line for the initial loading is extended to 413 kPa (where 1 kPa equals 0.145 psi) at 14 mm of settlement, and the reloading line is extended to 900 kPa at 70 mm of settlement.
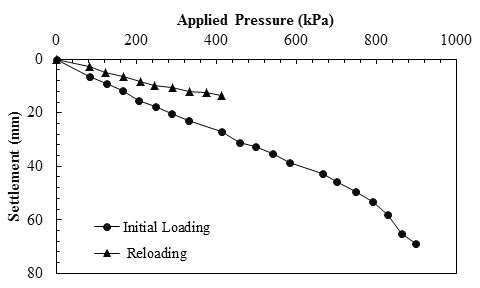
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Adams and Wu et al.(22,23)

Figure 51. Graph. Load-settlement curves for the pier.

 

This graph shows the lateral displacement measured by a linear voltage displacement transducer (LVDT). The y-axis shows pier height from 0 to 6 m, and the x-axis shows lateral displacement from 0 to 40 mm (where 1 mm equals 0.039 inch). The plot has three curved lines that represent the lateral displacement pattern of the pier under three different conditions: 415, 900, and 415 kPa reload (where 1 kPa equals 0.145 psi). At 415 kPa of applied pressure, the maximum lateral displacement of the pier is 8.0 mm at 3.3 m elevation (where 1 m equals 3.28 ft), and it has 3.5 mm deflection at its top at 4.8 m and 0.9 mm horizontal deflection at the bottom. At 900 kPa of applied pressure, the maximum lateral displacement is 34.2 mm at 2.5 m elevation, and it has 7.4 mm deflection at its top at 4.8 m and 11.3 mm horizontal deflection at the bottom. At 415 kPa reload case, the maximum lateral displacement is 8.5 mm at 2.5 m elevation, it has no deflection at its top and 1.7 mm horizontal deflection at the bottom.
1 ft = 0.305 m
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Adams and Wu et al.(22,23)

Figure 52. Graph. Lateral displacement measured by LVDT.

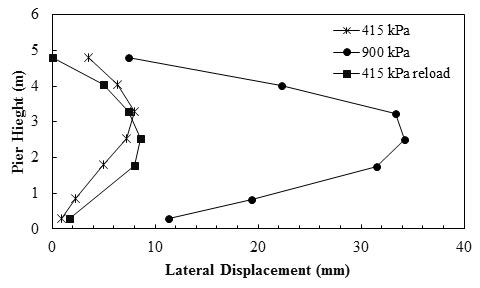
Two GRS bridge abutments were built in Black Hawk, CO, in 1997 to support a steel bridge.(23) Because the thickness of the reinforced soil abutment were different beneath the four footings directly supporting the weight of the bridge, the GRS abutment was preloaded to reduce the differential settlement between adjacent footings. The abutment was preloaded up to 35.53 psi (245 kPa) (1.6 times the design load of 21.76 psi (150 kPa)) for the square footing and 11.60 psi (80 kPa) (2 times the design load of 5.80 psi (40 kPa)) for the rectangular footing. It was found that preloading substantially reduced the differential settlement. The differential settlements at 21.76 psi (150 kPa) of the preloading cycle for the two abutments were 0.33 and 0.85 inch (8.4 and 21.6 mm). At 21.76 psi (150 kPa) in the reloading cycle, the differential settlement of both abutments was less than 0.039 inch (1 mm).(23) Measured results by Wu et al. also show that preloading reduced the lateral movement of GRS abutments (see figure 53 and figure 54).(23) At 21.76 psi (150 kPa) in the preloading cycle, the maximum lateral displacements in the west abutment (8.86 ft (2.7 m) tall) and the east abutment (17.72 ft (5.4 m) tall) were 0.06 and 0.52 inch (1.5 and 13.2 mm), respectively. These displacement values were reduced to 0.02 and 0.18 inch (0.6 and 4.5 mm), respectively, at 21.76 psi (150 kPa) in the reloading cycle. After the first reloading cycle, there was no significant reduction in the magnitude of the lateral and vertical deformations of the GRS abutments in the subsequent reloading cycles.(23)

This graph shows the lateral deformation profiles of the west abutment. The y-axis shows wall height from 0 to 3 m, and the x-axis shows lateral deformation from -8 to 4 mm (where 1 m equals 3.28 ft, and 1 mm equals 0.039 inch). The plot has three curved lines that lead from the origin and represent the lateral deformation pattern of the abutment under three different conditions: preloading at 150 and 250 kPa and reloading at 150 kPa (where 1 kPa equals 0.145 psi). The curve for preloading at 150 kPa reaches 1.5 mm deformation at 0.6 m elevation and then is extended to -1.8 mm deformation at a height of 2.4 m. The curve for preloading at 250 kPa reaches 2.2 mm deformation at 0.6 m elevation and then is extended to -6.2 mm deformation at a height of 2.4 m. The curve for reloading at 150 kPa reaches to 0.6 mm deformation at 0.6 m elevation and then is extended to 0.2 mm deformation at a height of 2.4 m.
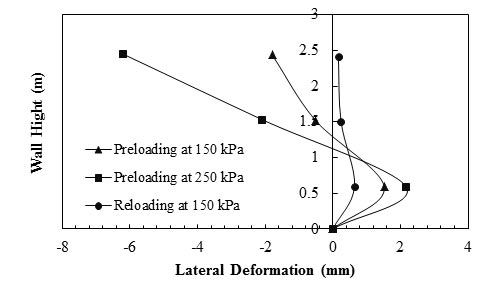
1 ft = 0.305 m
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Wu et al.(23)

Figure 53. Graph. Lateral deformation profiles of the west abutment.

 

This graph shows the lateral deformation profiles of the east abutment. The y-axis shows wall height from 0 to 4 m, and the x-axis shows lateral deformation from 0 to 35 mm (where 1 m equals 3.28 ft, and 1 mm equals 0.039 inch). The plot has three curved lines that lead from the origin and represent the lateral deformation pattern of the abutment under three different conditions: preloading at 150 and 250 kPa and reloading at 150 kPa (where 1 kPa equals 0.145 psi). The curve for preloading at 150 kPa reaches to the maximum deformation of 13.3 mm at 2.1 m elevation and then is extended to 4.7 mm deformation at a height of 3.3 m. The curve for preloading at 250 kPa reaches to the maximum deformation of 29.0 mm at 2.1 m elevation and then is extended to 9.9 mm deformation at a height of 3.4 m. The curve for reloading at 150 kPa reaches to the maximum deformation of 4.9 mm at 2.1 m elevation and then is extended to 3.1 mm deformation at a height of 3.3 m.
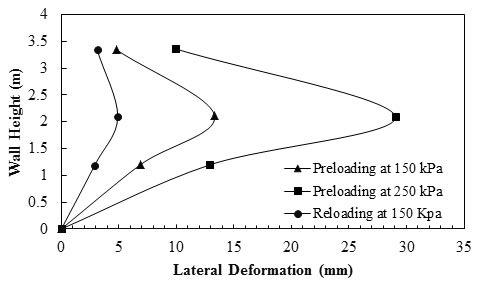
1 ft = 0.305 m
1 inch = 25.4 mm
1 psi = 6.89 kPa
Note: This figure was created by FHWA after Wu et al.(23)

Figure 54. Graph. Lateral deformation profiles of the east abutment.

 

3.4 Effects of Transient Loads on Deformations of Bridge Supports on Granular Soils

Live loads may include traffic load and compaction-induced load. Few research studies have investigated the effect of live loads on bridge supports using engineered fills. Based on a three-dimensional (3D) numerical study on an integral abutment bridge, Olson et al. concluded that superstructure deflections related to live load had a secondary effect on the abutment displacement but substantially changed their rotation.(80) As a result, the critical moments at the connection between superstructure and foundation were exacerbated by live load in thermal expansion and improved in thermal contraction conditions. Chapter 10 of AASHTO LRFD Bridge Design Specifications specification states, “Transient load may be omitted for settlement analysis for cohesive soils subjected to time-dependent consolidation settlement.”(8) However, for cohesionless soils (including engineered fills), transient load may be considered in the deformations of shallow foundations and abutments and piers of bridges. For retaining walls and bridge abutments, the traditional approach is to add the live load to the dead load and consider the combined loads as a permanent dead load. For example, through analytical studies, Kim and Barker and Esmaeili and Fatollahzadeh investigated the equivalent surcharge for truck load and train load, respectively, on retaining walls and bridge abutments.(81,82) Presently, the dynamic effect of transient load on bridge supports using engineered fills has not been investigated. Moreover, there is a lack of literature on the time-dependent and live (transient) load on the stress-deformation behaviors of bridge supports in engineered fills.

3.5 Determination of Stress Distributions in Granular Soils under Shallow Foundations

Equations to compute vertical stresses at any point in a soil mass due to external vertical loadings have been developed based on the theory of elasticity. The formulas that are most widely used are the Boussinesq and Westergaard formulas.(83,84) They were first developed for point loads acting at the surface. These formulas have been integrated to obtain stresses below uniform strip loads and rectangular loads. In the practice, Boussinesq’s formulas are often preferred, as they give conservative results.

The Boussinesq formulas are based on the following assumptions:(83)

In the Westergaard formulas, the material is isotropic with finite and equal horizontal and vertical normal moduli and Poison’s ratios but with infinite horizontal shear modulus.(84) The assumptions for Westergaard’s formulas are as follows:

For engineered fills without reinforcement, the Boussinesq and Westergaard formulas can be used to determine the stress distributions inside the soil mass. In reinforced engineered fills that are used as bridge supports, the reinforced soils are no longer isotropic or homogeneous. Therefore, the Boussinesq and Westergaard formulas may not be applicable. In such a case, numerical simulations (such as FEM or finite difference method) may be used. Many past researches have studied the strain and stress distributions of the reinforcements within geosynthetic-reinforced walls. (See references 85–88.) For metallic-reinforced soils, there are three common methods used in North American practice for estimating reinforcement loads: the AASHTO coherent gravity method, the FHWA structure stiffness method, and the AASHTO simplified method. (See references 52, 89, and 36.) Limited studies have been conducted on stress distributions in reinforced soils as bridge supports, particularly in SLS. Rowe and Ho studied a continuous full-facing panel wall with a hinged toe and reinforced with extensible reinforcement in a granular backfill resting on a rigid foundation.(90) This numerical study concluded that among the parameters examined, the distribution of force was most affected by the reinforcement stiffness, density, the external Φ between facing and soil, the backfill soil internal Φ, and the rigidity of the facing.

The stress distribution can be influenced by various soil conditions (i.e., grain size distribution, strength parameters, relative density, and fine content), reinforcement characteristics (i.e., Tf, stiffness, N, and Sv), and loading conditions, some of which were investigated by Rowe and Ho.(90) However, the literature search conducted by the authors of this report suggests there is a lack of documentation and understanding of the effects of various parameters on the stress distribution in reinforced engineered fills as bridge supports in SLS.

 

 

Return to top

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse | U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101