U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-093 Date: February 2018 |
Publication Number: FHWA-HRT-17-093 Date: February 2018 |
Before discussing the connection performance under cyclic structural loading, the parameters used in the analysis and evaluation of the section must first be introduced.
The full-scale testing conducted in this research was intended to simulate the stress conditions within the connections in a real bridge. When wheel loads are applied to a beam in a multi-beam bridge, the adjacent members are forced to deflect simultaneously as the load is transferred through the connection to adjacent beams. One of the key parameters investigated in this study is the proportion of the moment carried by the loaded beam. This is analogous to the moment distribution factor that by definition can be calculated using the equation in figure 34.
When the two beams have the same cross section, material properties, and boundary conditions, the moment carried by each beam is proportional to the deflection or the longitudinal tensile strain at the mid-span. In the four-point bending setup used in these tests, the relationship between the moment, the deflection, and longitudinal tensile strain are given in figure 35 and figure 36, respectively.
Where:
M = moment at the mid-span.
δ = deflection at the mid-span.
EI = beam stiffness.
l = span length.
b = distance from each end support to each loading point.
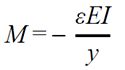
Figure 36. Equation. Moment carried by the beam with respect to the longitudinal tensile strain at the mid-span.
Where:
ε = longitudinal tensile strain at the mid-span.
y = distance from where the tensile strain is measured to the neutral axis of the cross section.
Given these relationships, the equation in figure 34 can be rewritten with respect to the mid-span deflection and longitudinal tensile strain for the two-beam system being employed in this study, as shown in figure 37 and figure 38, respectively.

Figure 37. Equation. Loaded beam proportion of moment factor with respect to the mid-span deflection.
Where:
δA = deflection of beam A.
δB = deflection of beam B.

Figure 38. Equation. Loaded beam proportion of moment factor for the loaded beam with respect to the mid-span longitudinal tensile strain.
Where:
εA = longitudinal tensile strain in beam A.
εB = longitudinal tensile strain in beam B.
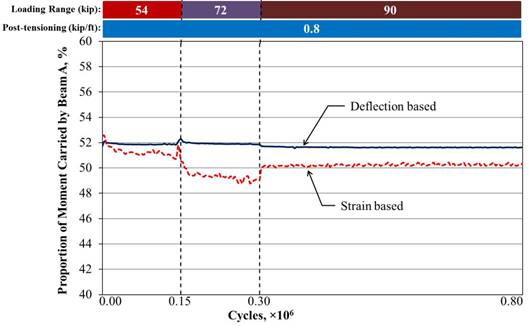
An example of the calculated loaded beam proportion of moment based on deflection and strain for the simply supported unstiffened beams with partial-depth conventional grout connection is presented in figure 39.
The deflection was recorded by the LVDTs placed at the mid-span, and the strain was measured with the embedded bottom longitudinal strain gauges at the mid-span. A total of 1.5 million cycles was included under three loading ranges. In this figure, beam A was cyclically loaded over three loading ranges spanning from 5 kip (22 kN) up to 59, 77, and 95 kip (262, 342, and 423 kN). The load on beam B was held constant at 5 kip (22 kN). The proportion of moment based on the strain and deflection agreed, showing that beam A carried about 52 percent of the total moment.
Figure 40 demonstrates the loaded beam proportion of moment for the same configuration with the addition of the partially stiffened boundary condition. In this case, the two beams still have the same support conditions, and the proportion of moment can be calculated using the equations in figure 35 and figure 36. As shown in figure 40, beam A had a proportion of moment close to 52 percent with the partially stiffened boundary condition, which was nearly identical to the unstiffened case. However, if the longitudinal strains in the beams are different, the moment transferred though the connection must be different. The proportion of moment itself may not reflect the difference, as it measures the ratio of the moments.
Source: FHWA.
1 kip = 4.448 kN.
1 kip/ft = 14.59 kN/m.
Figure 40. Graph. Loaded beam proportion of moment based on deflection and longitudinal tensile strain for partially stiffened beams with a partial-depth uncracked conventionally grouted connection.
For the fully stiffened configuration, the proportion of moment could not be calculated using the equations in figure 35 and figure 36 because the boundary conditions of the two beams were different. A new parameter, the equivalent moment transferred through the connection (Mequivalent), must be introduced. This is described further in the following subsection.
The concept of Mequivalent is demonstrated in the following example with the two simply supported beams loaded at the extreme values of the loading range. When beam A was loaded at the maximum, beam B had less deflection and tensile strain at the mid-span than beam A but more than if it had not been connected to beam A. This extra deflection and tensile strain in beam B was driven by the force transfer through the connection. Mequivalent represents the moment being transferred through the connection and can be calculated using the equations in figure 41 and figure 42 as follows:
Where:
ε′ = additional strain in beam B due to Mequivalent.
εmeasured = measured strain in beam B when beam A is loaded at the maximum load and beam B is loaded at the minimum load.
ε5kip = strain in beam B when both beams are loaded at 5 kip (22 kN).
Where EIeff is the effective beam stiffness.
ε′ can also be thought of as the range of strain experienced during a loading cycle. For the variables in the equations in figure 41 and figure 42, the strains are direct measurements, and y, which was previously defined in the equation in figure 36, is a property of the beam cross section. EIeff can be calculated using the equations in figure 35 and figure 36 with the measured deflection and strain. The calculation of EIeff is demonstrated in the following paragraphs and is compared with the theoretical values based on the sectional and material properties of the beam used.
After the two beams were grouted together, they were loaded, and the deflection and tensile strain at the mid-span were measured. The specimen was loaded with 45 kip (200 kN) on one beam and 55 kip (244 kN) on the other beam, which was equivalent to 50 kip (222 kN) on each beam. The mid-span deflection and tensile strain were recorded. These values were compared with the calculated values obtained using the equations in figure 35 and figure 36. The calculated deflection and tensile strain used an assumed value for the concrete’s modulus of elasticity based on an 8,000-psi (55-MPa) compressive strength.
The moment of inertia of the two connected beams was calculated as two times the moment of inertia of an individual beam based on the dimension and reinforcement details. The beam stiffness (EI) for a single beam was calculated to be 434 × 106 kip-inch2 (1.25 × 106 kN-m2). The calculated deflection and tensile strain were both slightly larger than the measured values, indicating EI was underestimated. This could be due to the solid diaphragms in the beams and the solid connection. EIeff was then calculated using the equations in Figure 35 and Figure 36 using the actual measured deflection and strain. The results are listed in table 9. EIeff based on deflection and tensile strain were 442 × 106 and 472 × 106 kip-inch2 (1.27 × 106 and 1.35 × 106 kN-m2), respectively, compared to the calculated EI of 434 × 106 kip-inch2 (1.25 × 106 kN-m2). The average of the two, 457 × 106 kip-inch (1.31 × 106 kN-m2), was used as the EIeff.
| P (kip) |
δcalculated (inches) |
δmeasured (inches) |
EIeff,δ (× 106 kip-inch2) |
εcalculated (με) |
εmeasured (με) |
EIeff,ε (× 106 kip-inch2) |
|---|---|---|---|---|---|---|
| 50 | 0.447 | 0.439 | 442 | 356 | 328 | 472 |
1 kip = 4.448 kN.
1 inch = 25.4 mm.
Where:
P = load at each load point (see figure 22 for loading setup).
δcalculated = calculated deflection of the beam.
δmeasured = measured deflection in beam B when beam A is loaded at the maximum load and beam B is loaded at the minimum level.
EIeff,δ = effective beam stiffness based on deflection measurements.
εcalculated = calculated strain.
εmeasured = measured strain in beam B when beam A is loaded at a maximum load and beam B is loaded at the minimum load.
EIeff,ε = effective beam stiffness based on strain measurements.
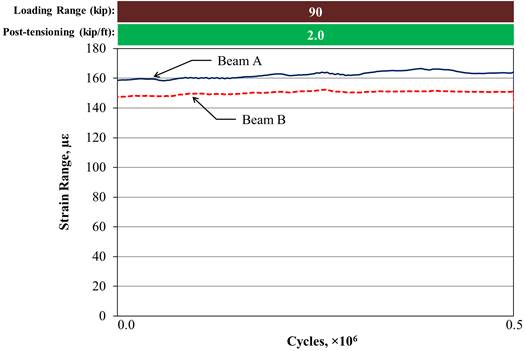
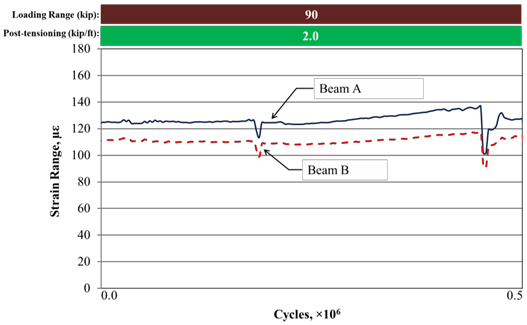
With the new parameter of Mequivalent, the effect of different boundary conditions was evaluated. For the unstiffened beams with a partial-depth conventionally grouted connection, the measured strain is presented in figure 43, while the strain for the same beams with the partially stiffened boundary condition is presented in figure 44. In both figures, beam A was loaded to 95 kip (423 kN), and beam B was loaded to 5 kip (22 kN). In the unstiffened case, beams A and B had average strains of 162 and 150 με, respectively. Mequivalent was 502 kip-ft (680 kN-m). For the partially stiffened case, beam A had an average strain of 127 με, and beam B had an average strain of 111 με. Mequivalent was 395 kip-ft (535 kN-m). The proportion of the moment carried by beam A for both boundary conditions was about the same even though the transferred moment differed.
Source: FHWA.
1 kip = 4.448 kN.
1 kip/ft = 14.59 kN/m.
Figure 43. Graph. Longitudinal tensile strain range at the mid-span for unstiffened beams with a partial-depth uncracked conventionally grouted connection.
Source: FHWA.
1 kip = 4.448 kN.
1 kip/ft = 14.59 kN/m.
Figure 44. Graph. Longitudinal tensile strain range at the mid-span for partially stiffened beams with a partial-depth uncracked conventionally grouted connection.
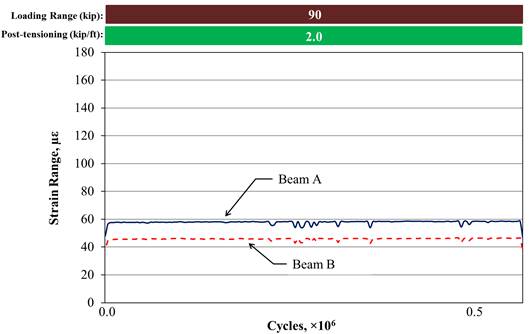
Figure 45 presents the strain for the same beams in the same loading range but with the fully stiffened boundary condition. This case was analyzed in two steps. The first step assumed that a single beam with the partially stiffened boundary was loaded with a total force of 95 kip (423 kN). The tensile strain at the mid-span can be reasonably estimated as the sum of the strains in beams A and B with the same boundary condition less the strain induced by a 5-kip (22-kN) load on both beams. ε5kip was measured to be 14 με, which yielded an estimated strain of 220 με. The corresponding moment can then be calculated using the equation in figure 36, which gives an Mequivalent of 681 kip-ft (920 kN-m). In the second step, the actual beam A in the case was investigated. The beam had the same boundary condition as in the first step, except a force was transferred through the connection, which generated a moment in the adjacent beam. Mequivalent at the mid-span of beam A can be calculated using the equation in figure 42, which was 183 kip-ft (248 kN-m) corresponding to a strain of 59 με. Therefore, the remaining 498 kip-ft (673 kN-m) of the 681 kip-ft (920 kN-m) was transferred through the connection compared to 395 kip-ft (535 kN-m) Mequivalent for the partially stiffened case. A more severe loading condition on the connection was created when the deflection of one beam was restrained.
Source: FHWA.
1 kip = 4.448 kN.
1 kip/ft = 14.59 kN/m.
Figure 45. Graph. Tensile strain range at the mid-span for fully stiffened beams with a partial-depth uncracked conventionally grouted connection.
The strain in beam A was reduced by nearly 55 percent from 127 to 59 με when the fully stiffened boundary condition was added to beam B compared to the partially stiffened case. This can be viewed as equivalent to the case limiting the end rotation but with 2.2 times of original stiffness. Thus, this loading configuration was similar to a case wherein 4.4 beams were connected in the system. Therefore, the stiffest condition created in the study was considered to approximate the case with 4.4 beams connected with a 95-kip (423-kN) load on a single exterior beam.
Δδ between adjacent beams is another factor that was evaluated in this study. It is defined by the authors as the difference between the deflections of these two lines at the interface between the two beams. This was done to remove the rigid body rotation of the beams. When connections deteriorate, beams do not deflect uniformly under live loads. Large Δδ between adjacent girders may lead to further degradation of grouted connections and reflective cracking in the overlay if one is present. Δδ is determined by checking the deflection measurements between the adjacent beams at the mid-span near the connection. Four vertical LVDTs were placed at the mid-span: two on each beam with each LVDT placed 2 inches (51 mm) from the edges of each beam. Δδ was determined by drawing two straight lines that define the bottom of each beam. Given where the four LVDTs are located, Δδ can be calculated with the equation in figure 46.
Where:
δAI = deflection from the loaded beam on the interior LVDT.
δAE = deflection from the loaded beam on the exterior LVDT.
δBI = deflection from the unloaded beam on the interior LVDT.
δBE = deflection from the unloaded beam on the exterior LVDT.
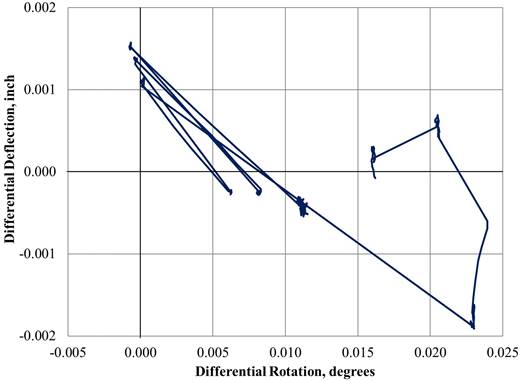
Due to this means of calculation, Δδ may become negative if the loaded beam rotates more than the unloaded beam. Differential rotation is defined by the authors as the rotation in the unloaded beam subtracted from the rotation in the loaded beam. Figure 47 shows an example of this behavior from the full-depth UHPC connection. It is evident that an increase in differential rotation can yield a decrease in Δδ.
Source: FHWA.
1 inch = 25.4 mm.
Figure 47. Graph. Comparison of Δδ and differential rotation for the full-depth UHPC connection.
A fully functioning connection is assumed to effectively transfer the load from one beam to the other. The adjacent beam is expected to have the same deflection as the loaded beam and, therefore, should have a nearly identical deformed shape. The loads that drive this behavior are transferred through the connection. The Canadian Bridge Code assumes that the load is transferred from one beam to another primarily through transverse shear. Transverse flexural rigidity is neglected.(10) This report uses the same assumption.
When two beams are connected and only one beam is loaded, the magnitude of the transverse shear force generated in the connection is related to the deflection of the beams. For a two-beam system where the load is applied to one beam, a greater deflection of the pair will generate more transverse shear in the connection. At locations where there is no potential deflection, such as at the beam ends, no transverse shear force will be generated. For the two beams analyzed in this study, the structurally loaded beam had a nearly uniformly deflected shape. One possible transverse shear distribution (Vy) is presented in figure 48. If Vy and the moment transferred through the shear key are known, the shear force transferred through the connection can be calculated. As the variable of interest for design is the maximum distributed shear force (v′max) in the connection, the shear force calculation can be simplified by assuming a triangular shear distribution (v′y). v′max of v′y should be larger than the maximum value of Vy. v′max can be calculated using the equation in figure 49.
Where:
Mmax = maximum moment transferred through the connection.
l = span length.
For the tests conducted in this study, Mmax was 478 kip-ft (646 kN-m), and v′max was calculated to be 207 lb/inch (36.3 kN/m).
The Canadian Bridge Design Code provides charts to determine the required transverse shear force to be resisted based on the study by Bakht et al.(10,39) In the method proposed by Bakht et al., the shear force is determined using the orthotropic plate theory based on the bridge width, span length, and a factor related to the longitudinal, flexural, and torsional rigidity of the beam section.(39) In general, bridges with greater torsional rigidity, larger bridge widths, and shorter spans generate higher transverse shear. Using the Canadian Bridge Design Code chart that aligns with the beams tested in this study, v′max due to the AASHTO HS-20 truck is calculated to be approximately 207 lb/inch (36.3 kN/m).(10,5) This used the minimum bridge width available in the charts, which is 25 ft (7.6 m).
The shear stress in the shear key can be calculated for the partial-depth conventionally grouted shear key. The depth of the shear key is 8.875 inches (225 mm), and v′max is 207 lb/inch (36.3 kN/m). Therefore, the shear stress is 23 psi (161 kPa).
The interface shear strength of the conventional grout to the precast concrete has been reported by other researchers. For example, a study by Buyukozturk et al. found that the shear strength at the interface between grout and concrete for a flat connection was 85 psi (590 kPa) under 100 psi (0.69 MPa) of confining pressure and increased to 210 psi (1.4 MPa) with 300 psi (2.07 MPa) of confining pressure.(40) They also found that the shear strength of a keyed connection would be 10 times greater than a flat connection under the same confinement pressure. Other studies found that the shear strength for keyed connections in the absence of transverse confinement can range from 150 to 358 psi (1.03 to 2.47 MPa).(41,42) Based on these values, the shear strength of a conventionally grouted connection is sufficient to transfer the estimated shear stress found in this study.
De la Varga et al. conducted ASTM C882 slant shear tests to determine the interface shear strength of UHPC materials.(17,43) They found that the bond between UHPC and concrete with an EA surface usually failed the concrete substrate. This suggests that the interface bond is stronger in shear compared to the precast concrete.