U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-16-064 Date: November 2016 |
Publication Number: FHWA-HRT-16-064 Date: November 2016 |
In recent years, bottleneck mitigation has been attempted through strategies such as ramp metering and variable speed limits (VSLs). This section presents recent research on the following five mitigation strategies, which are expected to be cost effective:
Some of the unpublished simulation datasets used to evaluate these strategies can be obtained by contacting the STOL at FHWA’s TFHRC.
In addition to the five featured strategies, the following alternative intersection and interchange designs are recommended:
According to chapter 23 of the 2016 HCM, alternative intersections are created by rerouting one or more movements from their usual places to secondary junctions.(45) Often, the rerouted movements are left turns (LTs). Alternative intersection and interchange designs have significantly reduced travel times and delays in many areas compared to conventional intersection designs. Some designs have substantially reduced the number of conflict points between vehicles, thus increasing overall safety. In addition, the alternative designs can often be implemented with minimal disruptions to existing right-of-way. Given the relatively low cost of implementation for many of these designs, the combination of improved mobility and safety has produced outstanding B/C ratios within economic analyses. By moving or eliminating problematic LT movements, the alternative designs have efficiently mitigated congestion at surface street-freeway interchanges and at signalized intersections. For more information, refer to FHWA’s Alternative Intersection and Interchange Report (AIIR) and Alternative Intersection Design Web site.(46,47)
According to the AIIR, DLT intersections tend to be more operationally efficient than RCUT and MUT intersections.(46) However, DLT intersections require a larger footprint than RCUT and MUT intersections and limit access along the displaced LT approaches. Regarding the alternative interchange designs (DDI and DLTI), DDI is more effective for unbalanced flows and heavy LT flows. DLTI is more favorable for heavy and balanced (opposing) through demands. It can handle also heavy LT volumes, although not as heavy as the DDI. FHWA’s Capacity Analysis for Planning of Junctions spreadsheet can be used for sketch planning comparison of alternative intersection and interchange designs.(48) Roundabouts are more operationally efficient than traffic signals at isolated locations with moderate, balanced flows on at least three approaches.In addition, roundabouts can be significantly safer than conventional signalized intersections.
Conventional traffic signal control assumes the intersection’s lane assignment configuration is fixed. DLG aims to adjust lane assignment based on fluctuating travel demand to further improve intersection capacity utilization. In previous studies, DLG has been proven effective for balancing lane-by-lane flows and for reducing intersection delays.(49,50) This report describes development of a software application, which automatically identifies candidates for DLT treatment based on intersection volume and signal timing. This report also compares identification criteria in terms of their ability to identify intersections that benefit the most from DLG. Pros and cons of the criteria are discussed along with suggestions about how the software should be applied. The candidate selection software is applied to a large number of intersections in the Northern Virginia area and is shown effective in identifying promising candidates for DLG treatment. Two case study intersections are then used to demonstrate the benefits of DLG. Figure 30 and figure 31 illustrate the potential efficiency created by changing lane use.
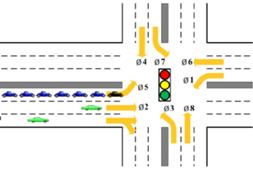
Figure 30. Illustration. Example of LT congestion prior to DLG.
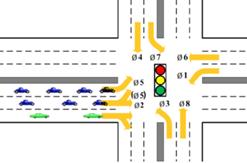
Figure 31. Illustration. Example of LT congestion after DLG.
To find candidate intersections having the greatest potential of being improved by DLG, a set of screening criteria needs to be defined. The criteria were developed and tested across 30 signalized intersections within four urban traffic networks in Northern Virginia. Each of the 30 research intersections had four approaches, and each approach had two target movements (LTs and right turns (RTs)). The through (TH) movement is not a target movement because the necessary number of downstream lanes typically would not exist. Intersections were analyzed within eight typical time periods: weekday morning, weekday off-peak, weekday midday, weekday afternoon, weekend morning, weekend afternoon, Saturday peak, and Sunday peak. Four screening criteria were developed: lane geometry, volume change, volume/lane (v/l), and v/c.
Safe Turning Geometry
When identifying intersections eligible for DLG treatment, safe turning geometry is a prerequisite screening criterion. For example, to convert a TH lane to a dedicated LT lane, two criteria would need to be met: (1) a receiving lane exists for the additional LT lane and (2) turn radii for opposing LT movements would not cause head-on collisions within the intersection. Data collection for this research automatically accounted for number of receiving lanes but did not automatically perform conflict analysis. In most intersection designs, the number of exit lanes matches the number of incoming TH lanes. Because converting exclusive LT or RT lanes into shared or exclusive TH lanes is usually not feasible, this research focuses on converting TH lane(s) into LT or RT lanes. To achieve this, there must be at least two TH lanes. If there is only one TH lane, the only option is converting it to a single shared lane, which tends to produce limited mobility benefits. For those reasons, the following two lane geometry conditions were chosen to qualify an LT or RT lane for DLG:
If the lane geometry criterion of an approach is not satisfied, that approach will be automatically excluded from DLG considerations.
Volume Change
The volume change screening criterion measures volume changes from one time period to another. Data collection for this research examined every possible combination of the eight time periods. If traffic volume patterns significantly differ between time periods, it implies one of the periods might qualify for DLG. Moreover, the absolute value of volume should be sufficiently high. For example, a volume increase from 10 to 20 vehicles/h is a 100 percent increase, but the absolute value of volume implies minimal benefit from a lane assignment change. In order to meet the volume change criterion, the equations shown in figure 32 through figure 34 should all be satisfied. Threshold values are set at 100 vehicles/h in figure 32 and 0.2 in figure 33 and figure 34, respectively. In the DLG software implementation, these values can be customized for local preferences.
![]()
Figure 32. Equation. Minimum acceptable demand volumes for DLG.
Where:
V = Demand volume.
TP1 = Time period 1.
TP2 = Time period 2.
![]()
Figure 33. Equation. Minimum change in turn volumes for DLG.
![]()
Figure 34. Equation. Minimum change in TH volumes for DLG.
v/l
This criterion compares the v/l of a LT or RT movement versus v/l of the adjacent TH movement. A criterion containing v/l is suggested as a surrogate measure of flow ratio (volume over saturation flow) because saturation flow rate data are not always readily available. The goal is to identify adjacent movements having significantly different flow ratios, and the criterion is shown in figure 35. In a DLG software implementation, the value of 1.5 could be customized for local preferences.
![]()
Figure 35. Equation. Different congestion in adjacent movements for DLG.
Unlike the volume change criteria, v/l does require data on existing lane groupings and further assumes that shared lanes (e.g., a shared LT and TH lane) are exclusive TH lanes. If there are no exclusive LT (or RT) lanes, the number of LT (or RT) lanes would be zero, and the v/l criterion would not be usable. However v/l is more sensitive to congestion levels than the volume change criteria.
v/c
The v/c criterion identifies how much capacity is utilized by each turning movement and should probably be used whenever signal timing information is available. DLG is most effective when v/c of the target LT or RT movement is sufficiently high, such that adding a TH lane significantly improves intersection operations. In addition, TH movement v/c should be sufficiently low, such that removing one lane does not generate undue congestion. The researchers found that when target LT or RT movement v/c exceeds 0.7, DLG tends to produce noticeable performance improvements. The TH movement should also be undersaturated (v/c lower than 1.0) after one lane is removed. Finally, if the target movement v/c is extremely high (e.g., over 1.3), it qualifies the approach for DLG regardless of TH movement v/c. Therefore, the criterion can be applied as follows: either the equations in figure 36 and figure 37 should both be satisfied or the equation in figure 38 should be satisfied.
![]()
Figure 36. Equation. Sufficient turn movement congestion for DLG.
![]()
Figure 37. Equation. Minimal TH movement congestion for DLG.
Where:
NLanes = Number of lanes.
![]()
Figure 38. Equation. Severe turn movement congestion for DLG.
The simplified calculation of (NLanes – 1)/Nlanes assumes all TH lanes are equally utilized because lane-by-lane queue length analysis may not be practical or available, especially when automatically screening hundreds of intersections. In the four criteria, v/c requires the most amount of data: volume, lane grouping, and existing signal timing. During the data analysis portion of this research, capacity values were obtained from Synchro®. The four screening criteria were coded into a JAVATM program, which imports input data from Synchro®. The JAVATM program can then report which intersections were flagged by each criterion.
The DLG screening software was tested across 30 intersections (from 4 urban traffic networks) in Northern Virginia. Intersection data were provided by the Virginia Department of Transportation (VDOT). Available at each intersection were traffic volume, signal timing, and v/c data for eight different time periods: weekday morning, weekday off-peak, weekday midday, weekday afternoon, weekend morning, weekend afternoon, Saturday peak, and Sunday peak. Each intersection had eight target LT and RT movements (two per approach). Thus, there were a total of 1,920 DLG candidates in the pool (30 × 8 × 8 = 1,920).
Table 4 displays the number of DLG candidates flagged by each of the screening criteria. Note that the number of candidates selected by lane geometry is not listed; this criterion was simply treated as a prerequisite to be met before consideration by the other criteria. Flagged candidates were then further studied within Synchro®. If no delay reduction was observed, that candidate was considered a false positive. Otherwise, the candidate was considered a true positive. The number of true positives is listed in parentheses in table 4. Some cells in the table have no parentheses, meaning those candidates were not analyzed due to time constraints. Table 4 shows that the v/c criterion flagged 24 candidates, and 22 of those were promising (true positive rate of 92 percent). True positive rates for the other two criteria were much lower. Within the OBN and TCN networks, true positive rates for the other criteria were lower than 20 percent.
| Selection Criteria | Traffic Network ID | Sum | |||
|---|---|---|---|---|---|
| A | B | C | D | ||
| Number of intersections | 7 | 10 | 8 | 5 | 30 |
| v/c criterion | 6(5) | 2(2) | 1(1) | 15(14) | 24(22) |
| v/l criterion | 4(1) | 42(7) | 22 | 68 | 136 |
| Volume change criterion | 4(2) | 12(1) | 15 | 30 | 61 |
| Note: The number in parentheses indicates how many of the candidates could be improved by DLG. | |||||
Table 5 lists flagged candidates in the OBN and TCN networks, along with the criteria that flagged them, and the corresponding delay reductions from applying DLG.
| Candidate ID | Network | v/c (Yes/No) |
V/L (Ye/No) |
Volume Change (Yes/No) |
Percent Delay Change |
Percent Delay Change (Optimized) |
|---|---|---|---|---|---|---|
| 1 | TCN | Yes | Yes | No | -4.5 | -4.2 |
| 2 | TCN | Yes | Yes | No | -1.7 | -0.7 |
| 3 | TCN | No | Yes | Yes | -1.7 | -2.0 |
| 4 | TCN | No | Yes | No | -5.9 | -0.6 |
| 5 | TCN | No | Yes | No | -4.6 | -4.6 |
| 6 | TCN | No | Yes | No | -2.6 | -3.1 |
| 7 | TCN | No | Yes | No | -2.1 | -2.1 |
| 8 | OBN | Yes | No | No | -8.2 | -8.2 |
| 9 | OBN | Yes | No | No | -5.0 | -10.4 |
| 10 | OBN | Yes | No | No | -8.3 | -10.5 |
| 11 | OBN | Yes | Yes | Yes | -14.0 | -20.6 |
| 12 | OBN | Yes | No | No | -9.8 | -20.7 |
| 13 | OBN | No | No | Yes | +12.9 | +9.2 |
The v/c criterion worked quite well in the OBN network, as its five flagged candidates showed delay reductions over 5 percent (candidate IDs 8–12). Candidate ID 11 was flagged by multiple criteria and exhibited the largest overall delay reduction. Candidate ID 13’s delay increased because the opposing LT had protected-permissive phasing. When the number of subject-approach TH lanes decreased from two to one, available gaps decreased on the remaining TH lane. As a result, LT delay on the opposing approach increased, cancelling out delay reductions on the subject approach. The v/l criterion flagged the largest number of candidates in the TCN network. Candidate IDs 3–7 were not flagged because v/c was lower than the 0.7 threshold. However, these candidates had minimal delay reductions (less than 6 percent). As shown in table 5, intersection delay reduction was less than 6 percent for all flagged candidates in the TCN network. Together, the proposed criteria captured different aspects of the intersection pattern. For example, the northbound (NB) approach at Davis Drive and Church Road (in Sterling, VA) has a dedicated LT lane, two TH lanes, and a dedicated RT lane. The v/l criterion flagged all eight periods of the NB LT movement. Converting a lane from TH to LT reduced intersection delay for all eight periods. However, none of the eight periods were selected by volume change. In summary, the Northern Virginia data collection implied that v/c flagged the top candidates as having the most potential for improvement under DLG. Candidates missed by v/c but flagged by other criteria either produced minimal benefits (less than 6 percent), or the intersection performance became worse.
This section presents detailed results for two promising candidates, which were flagged by the screening software. These case studies demonstrate the analysis process and clarify the performance improvements possible under DLG treatment.
Case Study 1
At the intersection of Reston Parkway and Sunrise Valley Drive (R&S), the afternoon peak westbound (WB) RT lane was flagged by v/c and v/l. Weekday morning and afternoon peak-hour volumes are shown in figure 39 and figure 40.
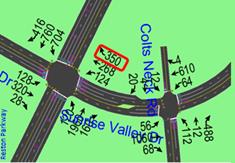
Figure 39. Illustration. Morning peak configuration for case study 1.
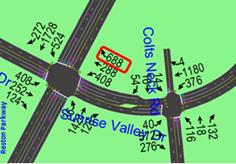
Figure 40. Illustration. Afternoon peak configuration for case study 1.
During the afternoon peak, there was heavy WB RT traffic (almost double the volume of the morning peak). Heavy RT volume exceeded capacity of the RT lane, causing a v/c of 1.56 and significant delays at the intersection. Moreover, a long queue on this approach degraded functionality of the adjacent upstream intersection (Colts Neck Road and Sunrise Valley Drive (C&S)). As a result, both intersections experienced significant delay during the afternoon peak. To improve the performance of these closely spaced intersections, the WB exclusive TH lane was converted to a TH+RT shared lane at R&S. Figure 41 and figure 42 illustrate the before-and-after lane configuration. The signal timing plan was then re-optimized to better handle this new intersection geometry. Both the existing and DLG lane assignments were simulated in SimTraffic™. Each lane assignment condition was simulated for five runs, having five sets of random number seeds. Each run simulated 1 h of traffic conditions.
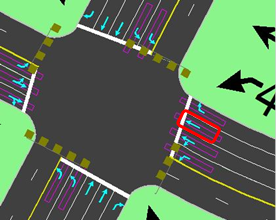
Figure 41. Illustration. Lane assignment before DLG for case study 1.
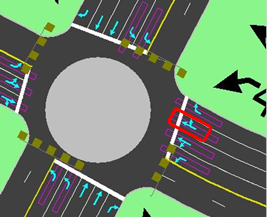
Figure 42. Illustration. Lane assignment after DLG for case study 1.
Table 6 lists the before-and-after delays at each intersection. It shows a reduction of total delay at the R&S intersection by 25.3 vehicle-h and at the C&S intersection by 44.0 vehicle-h during the 1-h simulation. Although the WB LT and TH movements performed worse at the R&S intersection under DLG, the WB RT improved, decreasing overall intersection delay. For the C&S intersection, performance of all WB movements was greatly improved. Based on the above analysis, DLG is suggested for weekday morning peak and afternoon peak hours.
| Traffic Delay | R&S Intersection | C&S Intersection | ||
|---|---|---|---|---|
| Existing | DLG | Existing | DLG | |
| WB LT delay/vehicle (s) | 69.7 | 104.2 | 84.2 | 68.6 |
| WB TH delay/vehicle (s) | 71.4 | 107.9 | 207.4 | 82.7 |
| WB RT delay/vehicle (s) | 77.8 | 73.1 | 318.8 | 121.7 |
| Total delay/vehicle (s) | 167.3 | 138.3 | 206.4 | 129.2 |
| Total delay (h) | 253.0 | 227.7 | 136.6 | 92.6 |
| Delay reduction (h) | 25.3 | 44.0 | ||
Case Study 2
For the intersection of Nutley Street and Lee Highway in Arlington, VA, whose turn movement volumes are shown in figure 43, the Sunday peak EB LT lane was flagged by all four screening criteria. The v/c ratio of this lane was 0.99, which is much higher than other time periods during the week. To improve the performance of this intersection, the left-most dedicated TH lane was converted to an exclusive LT lane. Under existing conditions, LTs move with permissive phasing. After the treatment, LTs can move with protected phasing. The timing plan was then reoptimized to better handle the new lane assignments. Each lane assignment condition was simulated for five runs having five sets of random seeds. Each run performed 1 h of traffic simulation.
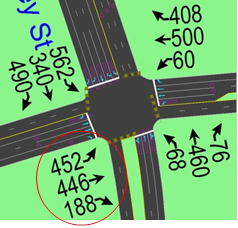
Figure 43. Illustration. Traffic demand for case study 2.
Table 7 lists the before-and-after delays for both intersections. The table shows a minor delay increase for the EB TH movement but a large delay reduction for the EB LT movement. This brings a total delay reduction of 15.9 h during the 1-h simulation. Therefore, dynamically converting a TH lane to a LT lane was beneficial during the Sunday peak hour.
| Traffic Delay | Nutley Street and Lee Highway Intersection |
|
|---|---|---|
| Existing | DLG | |
| EB LT delay/vehicle (s) | 147.0 | 78.3 |
| EB TH delay/vehicle (s) | 24.7 | 26.8 |
| EB RT delay/vehicle (s) | 8.9 | 9.2 |
| Total delay/vehicle (s) | 60.4 | 47.3 |
| Total delay (h) | 70.1 | 54.2 |
| Delay reduction (h) | 15.9 | |
The NB RT movement at the intersection of Shady Grove and North Frederick roads in Maryland has implemented a dynamic lane assignment strategy. Table 8 lists the discrepancy between morning peak and evening peak demands. The WB RT volume at 8 a.m. is 1,087 vehicles/h, while the same volume at 5 p.m. is only 678 vehicles/h. So during the morning peak, a dedicated TH lane is converted to RT.
A black-and-white dynamic message sign (DMS) over the dynamic lane at the intersection indicates whether the lane serves TH or RT traffic. When the white arrow is on, it means the lane is dedicated for RTs. Otherwise, it is a dedicated TH lane. Another sign 200 ft upstream of the intersection notifies drivers of dynamically assigned lanes ahead.
| Time | Number of Vehicles by Turning Movement | |||
|---|---|---|---|---|
| LT | TH | RT | Total | |
| 6 a.m. | 119 | 428 | 404 | 951 |
| 7 a.m. | 370 | 477 | 926 | 1,773 |
| 8 a.m. | 445 | 569 | 1,087 | 2,101 |
| 9 a.m. | 350 | 831 | 1,395 | 2,576 |
| 10 a.m. | 478 | 748 | 691 | 1,917 |
| 11 a.m. | 488 | 933 | 743 | 2,164 |
| 12 p.m. | 562 | 963 | 689 | 2,214 |
| 1 p.m. | 567 | 1,096 | 820 | 2,483 |
| 2 p.m. | 701 | 1,236 | 844 | 2,781 |
| 3 p.m. | 660 | 1,070 | 568 | 2,298 |
| 4 p.m. | 1,092 | 1,757 | 495 | 3,344 |
| 5 p.m. | 950 | 1,865 | 678 | 3,493 |
| 6 p.m. | 1,030 | 1,862 | 629 | 3,521 |
| Note: Bold values indicate peak period demands. | ||||
When performing B/C analyses, determining the monetary value of travel time and delay reduction is a first step. The SHRP2 report, Identification and Evaluation of the Cost-Effectiveness of Highway Design Features to Reduce Nonrecurrent Congestion, reviewed travel time monetization research.(51) One conclusion was that personal travel time (including commuter travel) should be valued at 50 percent of the prevailing wage rate. The report further cited a national wage rate of $21 per hour in 2009. Assuming an average occupancy of 1.6 persons per vehicle, hourly savings would be $17/vehicle-h as shown in figure 44.
![]()
Figure 44. Equation. Monetary savings for each vehicle-hour of delay reduction.
In case study 1, DLG saved 69.3 vehicle-h of delay. The closely spaced pair of intersections in case study 1 served approximately 6,800 vehicles during the peak hour. Therefore, assuming a cost of $17 per vehicle-h for 2015, total hourly time savings would be $1,178 as shown in figure 45.
![]()
Figure 45. Equation. Total hourly time savings for the DLG example.
DLG would presumably be implemented where lane grouping is effective during the morning peak period but ineffective during the afternoon peak (or vice-versa). Thus, it seems appropriate to assume these cost savings would only materialize during one peak period per day. If the number of commuting days per year is derived by excluding weekends and holidays, then the annual cost savings attributed to DLG could be as follows:
![]()
Figure 46. Equation. Annual cost savings for the DLG example.
Case study 2 revealed a more modest delay reduction of 15.9 vehicle-h. Repeating the cost calculations for case study 2 yields savings of $67,575 per year. Based on these results, it appears the DLG treatment may yield greater benefits at high-volume intersections (e.g., 6,800 vehicles/h) versus low-volume intersections (e.g., 4,100 vehicles/h).
Thus, in deciding whether or not to implement DLG strategies, annual benefits in the range of $68,000 (low-volume intersection) to $295,000 (high-volume intersection) would need to be compared against the costs of DLG implementation. These implementation costs would include the cost of installing and maintaining a DMS at the signalized intersection. It could also include the engineering analysis costs of applying the screening criteria (to identify candidate intersections) plus law enforcement (if any) for the new lane use.
Regarding the cost of installing and maintaining a DMS, the U.S. Department of Transportation (USDOT) Knowledge Resources Web site contains a list of unit cost entries for DMS.(52) These DMS costs vary widely from $10,000 to $200,000, but the signalized intersection DMS would presumably be less expensive than the freeway installations. Ideally, lifecycle maintenance and operation costs for the DMS would also be considered. A search for “DMS price” on the FHWA Web site leads to the USDOT ITS Benefits, Costs, and Lessons Learned Database, and some of the relevant prices are summarized in table 9.(52)
| Type of DMS | Capital Cost (Thousands of U.S. Dollars) | Operating Cost (Thousands of U.S. Dollars) |
|---|---|---|
| DMS | 47–117 | 2.4–6 |
| DMS tower | 25–120 | |
| DMS—portable | 18–25 | 1.2-2 |
| Note: Blank cell indicates data were not found. | ||
The USDOT ITS Benefits, Costs, and Lessons Learned Database further states the following:
According to FHWA’s Operations Benefit/Cost Analysis Desk Reference, many current B/C analysis tools use average annual benefits and costs in their analyses.(53) It was previously indicated that annual benefits would be in the range of $68,000 (low-volume intersection) to $295,000 (high-volume intersection). VDOT assumes a 15-year lifespan for DMS signs. In addition to the DMS (approximately $25,000) located above the intersection, it is helpful to have an upstream DMS (another $25,000) with its own mast arm (approximately $75,000). Assuming a signalized intersection DMS would have a total capital cost of $125,000, anticipated useful life of 15 years, and annual operations and maintenance (O&M) costs of $2,000 per year, the average annual cost and benefits would be as follows:
These are mobility-based B/C ratios not accounting for safety and environmental impacts. These ratios also assume that DLG is only applied to intersections flagged as good candidates for DLG treatment according to the screening process.
The following guidance is suggested for safe and efficient implementation of DLG.
Geometric Design
DLG is intended for implementation within existing roadways with no need for new curb cuts or alignment. However, as described previously, safe turning geometry is a prerequisite for DLG treatment. For example, to convert a TH lane to a dedicated LT lane, three criteria would need to be met: (1) a receiving lane exists for the additional LT lane, (2) turn radii for opposing LT movements would not cause head-on collisions within the intersection, and (3) the proposed lane grouping is compatible with any bicycle and pedestrian facilities present.
Signing
Black-and-white regulatory lane-use signs are essential to convey lane use, both at the intersection and in advance of the intersection, when the lane configuration is not defined by default rules of the road. The advance notification is especially critical in a dynamic situation where drivers may not expect a change. The use of traffic signal indications can supplement but not replace the regulatory signs. Figure 47 illustrates an example of upstream signage for DLG in the middle lanes. In this case, an overhead DMS is helpful because it sits directly above the affected lane. Regardless of which lane is dynamically controlled, similar DLG signage is needed at the intersection stop line to reinforce the message.

Figure 47. Photo. Upstream DLG signage in Maryland.
Striping
It is perhaps best for dynamically grouped lanes to not have painted turn movement arrows on the pavement, as this would introduce a contradiction with the DMSs and/or signal displays. The DLG treatment could theoretically benefit from electronic lighted striping where exclusive and shared-lane arrows could be dynamically superimposed on the roadway.
Signalization
During the DLG study that contributed to this report, the research team recorded hours of video at the Shady Grove intersection in Maryland. The videos indicated that some vehicles avoided the dynamically controlled RT lane and showed a strong preference for the statically controlled conventional RT lane. It was theorized that this could be in part due to the green ball signal display above the inside RT lane. When drivers see a green ball, they are conditioned to expect a TH movement. This signalization also conflicts with the DLG-based DMS above the inside lane, suggesting that an RT movement is allowed. When conflicting messages are present, drivers may have a tendency to obey the traditional signal display, as opposed to the less-common DMS. Thus, in cases like this, shared TH and RT arrow signalization could improve lane utilization and further reduce delay at the intersection. In addition, eliminating the contradictory messages (i.e., given by the green ball and the DMS) could help to improve safety. Similar benefits could be obtained for shared TH and LT cases. However, the nature of protected and permissive LT movements introduces new ramifications.
At arterial intersections, traffic demand may vary significantly by time, and the lane assignments designed for severe peak-hour traffic might not suit these different demand patterns. DLG can reduce the gap between supply and demand by dynamically changing lane assignments. This study developed a software tool with four screening criteria to quickly and easily identify intersections to benefit from DLG. It was found that v/c was shown to be the most effective criterion, with a true positive rate exceeding 90 percent and flagged candidates showing noticeable delay reductions. The volume change criterion appears helpful for identifying significant volume changes between time periods. The v/l criterion works similar to v/c but does not need signal timing data. In the two case studies, DLG reduced the overall intersection delay by approximately 20 percent. For agencies that manage intersections’ signal timing and lane assignments, there is a B/C tradeoff. The v/c criterion requires the most data but can pinpoint the most promising candidates. If an agency wants to identify as many promising intersections as possible, it should use the full set of criteria and spend more time analyzing the flagged candidates. Future research will include enhancing the software tool to automatically select DLG treatments and estimate benefits accordingly. Another direction of future work is to develop a real-time DLG protocol capable of changing both lane assignments and signal timing based on predicted traffic volume data.
In response to growing traffic congestion, an increasing number of active traffic management (ATM) strategies have been developed and implemented internationally. Among these strategies are HSR, VSLs, queue warning, dynamic truck restrictions, ramp metering, managed lanes, dynamic rerouting, traveler information, and DJC. These strategies are capable of monitoring traffic flow and can dynamically control speeds, reduce capacity drops, and inform road users of network conditions to optimize traffic and safety performance.
Of these strategies, DJC represents a component of the ATM system. It can be used at freeway off- and on-ramps to dynamically change lane allocation for interchanges. This report focuses on DJC and other potentially underrated strategies as opposed to popular strategies like ramp metering, which have been extensively researched and implemented in recent decades. The rationale for use is that in some traffic conditions or during certain times of day, it may be more effective to use existing downstream or upstream lanes for one type of movement or for traffic coming from the main lanes. At other times of day, it may be more effective to use the TH lanes to accommodate ramp merging, as illustrated in figure 48.(54)

Source: Schneider Electric and RK&K.
Figure 48. Illustration. DMC.(55)
One component of DJC strategies is DMC. When ramp congestion is high and mainline congestion is medium, hesitation and gap-finding delays may be disruptive to ramp capacities and flows, thus creating rear-end collision potential on the ramp. Alternatively, lane drops in the merge area can easily cause a bottleneck, leading to upstream congestion on both roads. In this situation, closing a lane on the lower-volume road would reduce or eliminate the friction caused by “weaving” (gap acceptance) movements in the merge area. As such, the DMC strategy is hypothesized to reduce traffic congestion at the merge of two freeways.
DMC is currently used in Germany and the Netherlands. Lane control signs are installed over both approaches upstream of the merge. Priority is given to the higher volume entrance. This strategy produces a more uniform traffic flow, with fewer conflicts and safer maneuvers.(56) There is no current implementation of DMC in the United States. In the 2014 Greater Richmond Safety and Mobility Study, DMC was considered for the two interchanges between I-95 and I-64 (Bryan Park and Shockoe Valley).(57) B/C analysis, however, revealed that deployment at Bryan Park would have adverse impacts and should not be implemented. Conversely, DMC implementation at Shockoe Valley was expected to have positive net impacts if planned modifications at the Chamberlayne interchange were implemented. One study suggested certain conditions should be met before applying DMC, including: (1) level of service (LOS)[2] F on entrance ramps for 2 consecutive hours during morning and afternoon peak periods, (2) over 1,200 vehicles/h on a single-lane on-ramp or over 2,000 vehicles/h on a two-lane on-ramp, and (3) LOS D or better on the upstream mainline lanes following implementation of DMC.(58) Research by TTI suggests it is preferable to have at least 900 vehicles/h on the single-lane on-ramp and LOS E or better on the mainline lanes following DMC implementation.(59) This research investigated the efficiency of DMC for common freeway-to-freeway and freeway-ramp merge geometries.
One set of freeway-to-freeway experiments involved multiple two-lane sections merging into three lanes (route A). In a second set of experiments, a three-lane section merged into a two-lane section to become four lanes (route B). Scenarios closing mainline lanes and ramp lanes were investigated with traffic demand variations. Table 10 describes the lane configurations and traffic demand variations for each freeway-to-freeway lane closing alternative. Figure 49 through figure 52 show the basic geometries for all freeway-to-freeway lane configurations and lane closing alternatives.
| Lane Closing Route | Route A | Route B | ||
|---|---|---|---|---|
| Number of Lanes | Volume (vehicles/h) |
Number of Lanes | Volume (vehicles/h) |
|
| Route A | 2 | 1,000–2,200 (by 200) | 2 | 2,400–4,600 (by 200) |
| 3 | 2,500–4,600 (by 300) | 2 | 3,000–4,600 (by 200) | |
| Route B | 2 | 2,400–4,600 (by 200) | 2 | 1,000–2,200 (by 200) |
| 3 | 4,200–6,500 (by 300) | 2 | 1,000–2,400 (by 200) | |
| Note: Volume was increased in increments of 200 or 300 vehicles/h to create a thorough set of testing scenarios (indicated by number in parentheses). | ||||
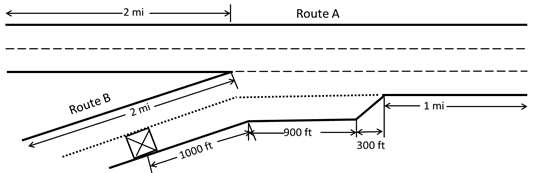
Figure 49. Illustration. Merging of multiple two-lane freeways (closure on route B).
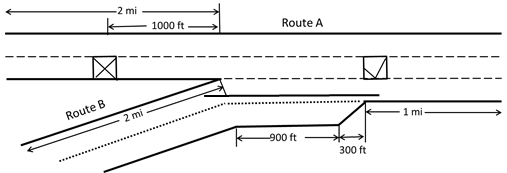
Figure 50. Illustration. Merging of multiple two-lane freeways (closure on route A).
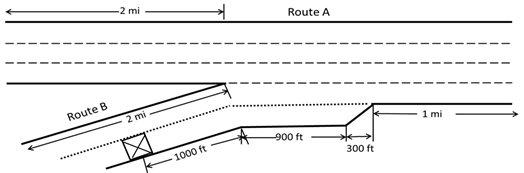
Figure 51. Illustration. Merging of three- and two-lane freeways (closure on route B).
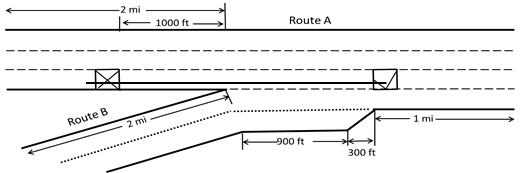
Figure 52. Illustration. Merging of three- and two-lane freeways (closure on route A).
Table 11 describes the lane configurations and traffic demand variations for freeway on-ramp merges. Figure 53 through figure 55 show basic geometries for the on-ramp scenarios considered in this research. The selected lane configurations covered the most common designs in the United States.
| Mainline | On-ramp | |||
|---|---|---|---|---|
| Number of Lanes | Volume (vehicles/h) |
Number of Lanes | Volume (vehicles/h) |
|
| 2 | 1,000–2,400 (by 200) | 1 | 1,000–2,000 (by 200) | |
| 3 | 2,100–4,800 (by 300) | 1 | 1,000–2,000 (by 200) | |
| 4 | 4,800–7,200 (by 400) | 1 | 1,000–2,000 (by 200) | |
| Note: Volume was increased in increments of 200 or 300 vehicles/h to create a thorough set of testing scenarios (indicated by number in parentheses). | ||||
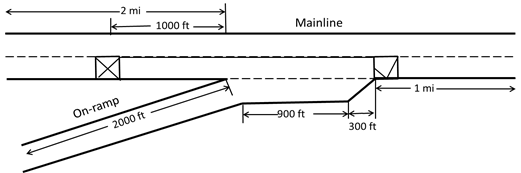
Figure 53. Illustration. Merging of one-lane ramp and two-lane mainline (closure on mainline).
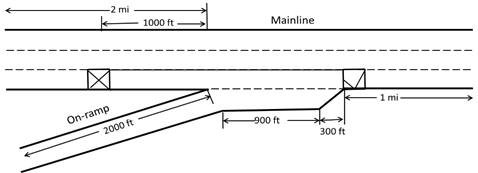
Figure 54. Illustration. Merging of one-lane ramp and three-lane mainline (closure on mainline).
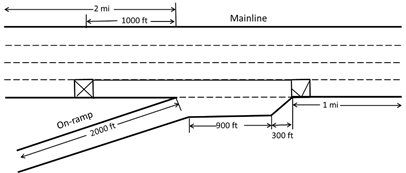
Figure 55. Illustration. Merging of one-lane ramp and four-lane mainline (closure on mainline).
Micro-simulation software VISSIM ™ was used to simulate road network performance under various scenarios. The simulation period for each scenario was 8,400 s, including 1,200 s of warm-up time. In each scenario, traffic demands on both roads were assumed to be fixed over the entire simulation period. Each scenario was simulated 15 times with 15 sets of random number seeds. Preliminary tests indicated that, for most scenarios, simulation results would converge after approximately 9–10 runs. For DMC cases, drivers were notified of lane closures 2,500 ft upstream of the lane closing point. Vehicle characteristics and driving behaviors were based on a precalibrated network (VA 267 merging with I-66 in Northern Virginia), which represents a typical freeway-to-freeway merge. The calibration process is briefly summarized as follows:
The following three criteria were employed for calibration: (1) relative root mean square error (RRMSE) for flow, (2) FHWA Geoffrey E. Havers (GEH) criteria, and (3) accumulated flow.
RRMSE for Flow
It was assumed that a traffic state parameter had values from field data and simulated data, as shown in figure 56.
![]()
Figure 56. Equation. Simulated values and mean values over all simulation replications.
In the simulation experiment, 10 replications were used for each day. RRMSE is defined by the equation in figure 57 as follows:
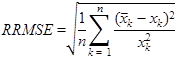
Figure 57. Equation. RRMSE.
Where:
n = Total number of simulation replications.
k = ID number for the current simulation replication.
![]() = Mean performance measure value of all simulation replications.
= Mean performance measure value of all simulation replications.
xk = Performance measure value of the current simulation replication.
FHWA GEH Criteria
The GEH statistic is calculated at each time point, k, as shown in figure 58 as follows:
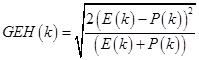
Figure 58. Equation. FHWA GEH criteria.
Where:
E = Expected performance measure value at time k as predicted by the traffic model.
P = Actual performance measure value at time k as measured in the field.
Then the percentage of aggregated time points which satisfy this condition can be calculated according to different traffic situations.
Accumulated Flow
RRMSE was not adequate to measure closeness of the model because if the error is biased, RRMSE could remain small, but accumulated error over time could be large. For example, if on-ramp or mainline upstream flows were persistently smaller than field-measured flows, many vehicles would be blocked outside the system, and the system would not represent real traffic. It was thus decided to use both RRMSE and accumulated flow for flow calibration. This is also applicable to the GEH criterion. Vehicles’ parameter values and their variances or thresholds should come from measured data such as headway and its variance, vehicle acceleration-deceleration capabilities, and driver response time. For this research, parameters were selected by analyzing Next Generation Simulation and/or Berkeley Highway Lab data on headway, jam density, and other measures.(60,61) Table 12 shows the driving behavior parameters that were employed in this study.
| Parameter | Freeway | On-Ramp | Merge |
|---|---|---|---|
| Maximum look ahead distance (ft) | 692.65 | 820.21 | 1,169.26 |
| Number of observed preceding vehicles | 2 | 2 | 2 |
| Average standstill distance (ft) | 4.30 | 9.61 | 9.19 |
| Headway at a certain speed (s) | 0.90 | 1.28 | 1.23 |
| Longitudinal oscillation (ft) | 11.12 | 6.14 | 7.12 |
| Start of the deceleration process | 8.00 | 8.00 | 8.00 |
| Acceleration behavior at 50 mi/h (ft/s2) | 4.92 | 4.92 | 4.92 |
| Maximum deceleration for leading vehicle (ft/s2) | 6.04 | 9.97 | 6.59 |
| Reduction of 3.28 ft/s2 deceleration per distance interval for leading vehicle (ft) | 62.53 | 100.83 | 120.40 |
| Accepted deceleration for leading vehicle (ft/s2) | 1.48 | 6.76 | 3.22 |
| Maximum deceleration for following vehicle (ft/s2) | 5.09 | 4.10 | 3.54 |
| Reduction of 3.28 ft/s2 deceleration per distance interval for following vehicle (ft) | 16.07 | 31.04 | 27.33 |
| Accepted deceleration for following vehicle (ft/s) | 4.49 | 2.92 | 0.95 |
| Minimum headway (ft) | 3.94 | 5.77 | 1.84 |
| Safety distance reduction factor | 0.14 | 0.20 | 0.23 |
| Maximum deceleration for cooperative braking (ft/s) | 11.35 | 11.81 | 13.75 |
| Maximum speed difference for cooperative braking (ft/s) | 15.99 | 12.62 | 10.04 |
| Maximum collision time for cooperative braking (s) | 7.22 | 6.80 | 9.25 |
This section presents the DMC simulation sensitivity analysis results for freeway-to-freeway merge area scenarios. The freeway with heavier demand is called route A (i.e., route B has lighter demand than route A). In some of the experiments, route A had two mainline lanes. In other experiments, route A had three mainline lanes. In some of the experiments, lane closure was applied to route A. In other experiments, lane closure was applied to route B. Therefore, this section presents results for four combinations of mainline lane numbers and lane closure.
Lane Closure on Route B—Three Lanes Merging with Two Lanes
Traffic demands were varied on route A from 4,200 to 6,600 vehicles/h in increments of 300 vehicles/h and on route B from 1,000 to 2,400 vehicles/h in increments of 200 vehicles/h. Preliminary analysis indicated negative effects of DMC when traffic demands on route A were 5,700 vehicles/h or less. A possible reason could be that the total volume of routes A and B did not exceed capacity in the merging area. To identify accurate thresholds, traffic demands of 5,800, 5,900, 6,400, and 6,500 vehicles/h on route A were tested against the same range of demands on route B (1,000 to 2,400 vehicles/h).
Table 13 presents the average vehicle delay (AVD) savings. Mean differences were obtained by subtracting AVD under DMC conditions from the corresponding base conditions. A positive value indicates a reduction of AVD by implementing the DMC strategy.
| Route B Demand (vehicles/h) | Experimental Result | Route A Demand (vehicles/h) | |||||
|---|---|---|---|---|---|---|---|
| 5,800 | 5,900 | 6,000 | 6,300 | 6,400 | 6,500 | ||
| 1,000 | AVD (s) | 0.09 | 0.15 | 0.00 | 0.78 | 2.47 | 4.89 |
| Percent change | +1 | +2 | +0 | +9 | +23 | +36 | |
| 1,200 | AVD (s) | 0.14 | 0.15 | 0.08 | 2.21 | 3.81 | 17.72 |
| Percent change | +2 | +2 | +1 | +22 | +31 | +67 | |
| 1,400 | AVD (s) | 0.26 | 0.46 | 0.26 | 6.06 | 12.69 | 38.42 |
| Percent change | +4 | +6 | +3 | +42 | +60 | +80 | |
| 1,600 | AVD (s) | 0.31 | 0.69 | 1.26 | 13.97 | 41.35 | 71.68 |
| Percent change | +4 | +8 | +14 | +62 | +82 | +88 | |
| 1,800 | AVD (s) | 0.7 | 1.3 | 2.49 | 47.15 | 77.35 | 96.92 |
| Percent change | +8 | +14 | +24 | +84 | +88 | +88 | |
| 2,000 | AVD (s) | 1.41 | 3.65 | 9.63 | 83.27 | 98.09 | 99.56 |
| Percent change | +15 | +30 | +52 | +87 | +86 | +78 | |
| 2,200 | AVD (s) | 4.13 | 10.45 | 26.82 | 93.92 | 94.3 | 80.98 |
| Percent change | +31 | +52 | +73 | +81 | +73 | +59 | |
| 2,400 | AVD (s) | 3.35 | 17.01 | 40.65 | 62.95 | 46.29 | 26.02 |
| Percent change | +15 | +45 | +60 | +48 | +33 | +18 | |
Lane Closure on Route A—Three Lanes Merging with Two Lanes
Traffic demands were varied on route A from 2,500 to 4,600 vehicles/h in increments of 300 vehicles/h and on route B from 3,000 to 4,600 vehicles/h in increments of 200 vehicles/h. Paired t-tests were conducted to determine whether AVDs under DMC significantly differed from base conditions. These t-tests were based on results of 15 simulation runs for base and DMC conditions. Results indicated that all delay differences between base and DMC conditions were statistically significant. Table 14 shows that when route B traffic demands exceeded 4,000 vehicles/h (around 2,000 vehicles/lane), closing a mainline lane reduced AVD regardless of demands on route A. The table also shows that benefits increased as traffic on route B increased.
| Route B Demand (vehicles/h) | Experimental Result | Route A Demand (vehicles/h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2,500 | 2,800 | 3,100 | 3,400 | 3,700 | 4,000 | 4,300 | 4,600 | ||
| 3,000 | AVD (s) | 0.48 | 0.49 | 0.49 | 0.53 | 0.51 | 0.57 | 0.58 | 0.53 |
| Percent change | 9 | 9 | 8 | 9 | 8 | 8 | 8 | 6 | |
| 3,200 | AVD (s) | 0.78 | 0.82 | 0.87 | 0.9 | 1.01 | 1.14 | 1.29 | 2.06 |
| Percent change | 13 | 13 | 14 | 13 | 14 | 15 | 15 | 21 | |
| 3,400 | AVD (s) | 1.22 | 1.23 | 1.28 | 1.39 | 1.59 | 1.87 | 2.42 | 4.6 |
| Percent change | 18 | 18 | 18 | 19 | 20 | 22 | 25 | 36 | |
| 3,600 | AVD (s) | 1.71 | 1.88 | 1.91 | 2.72 | 2.43 | 2.98 | 5.49 | 21.38 |
| Percent change | 23 | 24 | 24 | 30 | 27 | 30 | 42 | 72 | |
| 3,800 | AVD (s) | 2.74 | 5.88 | 7 | 8.65 | 6.88 | 26.48 | 42.69 | 88.95 |
| Percent change | 31 | 49 | 52 | 57 | 50 | 78 | 85 | 91 | |
| 4,000 | AVD (s) | 24.76 | 44.54 | 35.04 | 59.16 | 69.06 | 83.5 | 99.48 | 111.18 |
| Percent change | 80 | 87 | 84 | 90 | 91 | 92 | 93 | 93 | |
| 4,200 | AVD (s) | 83.46 | 91.21 | 89.06 | 102.04 | 101.81 | 107.54 | 112.65 | 119.1 |
| Percent change | 92 | 93 | 93 | 93 | 93 | 93 | 93 | 93 | |
| 4,400 | AVD (s) | 119.45 | 115.46 | 114.49 | 111.48 | 114.15 | 113.93 | 115.11 | 121.88 |
| Percent change | 94 | 94 | 94 | 93 | 93 | 93 | 93 | 93 | |
| 4,600 | AVD (s) | 124.42 | 122.58 | 119.66 | 117.89 | 115.97 | 116.14 | 119.01 | 122.02 |
| Percent change | 94 | 94 | 93 | 93 | 93 | 93 | 93 | 92 | |
Lane Closure on Route A—Two Lanes Merging with Two Lanes
Traffic demands were varied on route A from 1,600 to 2,400 vehicles/h in increments of 200 vehicles/h and on route B from 3,000 to 4,600 vehicles/h in increments of 200 vehicles/h. Table 15 shows that when traffic demands on route B exceeded 3,800 vehicles/h (around 1,900 vehicles/lane), closing a mainline lane improved AVD, average speed, and total throughput regardless of route A traffic demands. The table also shows that benefits increased as route B traffic increased.
| Route B Demand (vehicles/h) | Experimental Result | Route A Demand (vehicles/h) | ||||
|---|---|---|---|---|---|---|
| 1,600 | 1,800 | 2,000 | 2,200 | 2,400 | ||
| 3,000 | AVD (s) | -0.97 | -7.53 | -22.91 | -30.25 | -75.96 |
| Percent change | -12 | -89 | -254 | -314 | -734 | |
| 3,200 | AVD (s) | -0.53 | -6.78 | -21.41 | -28.53 | -72.99 |
| Percent change | -6 | -71 | -209 | -260 | -607 | |
| 3,400 | AVD (s) | -0.12 | -5.71 | -19.82 | -26.25 | -67.75 |
| Percent change | -1 | -51 | -168 | -204 | -464 | |
| 3,600 | AVD (s) | 0.47 | -4.08 | -16.41 | -22.68 | -45.61 |
| Percent change | 4 | -30 | -107 | -139 | -127 | |
| 3,800 | AVD (s) | 11.07 | 6.31 | 1.72 | 46.12 | 41.79 |
| Percent change | 45 | 23 | 5 | 54 | 33 | |
| 4,000 | AVD (s) | 62.89 | 92.37 | 110.01 | 155.25 | 188.15 |
| Percent change | 63 | 72 | 66 | 73 | 65 | |
| 4,200 | AVD (s) | 119.91 | 109.23 | 147.89 | 194.82 | 179.98 |
| Percent change | 42 | 36 | 44 | 52 | 43 | |
| 4,400 | AVD (s) | 115.84 | 134.42 | 126.34 | 170.36 | 192.92 |
| Percent change | 26 | 29 | 27 | 33 | 35 | |
| 4,600 | AVD (s) | 109.13 | 99.38 | 123.61 | 138.10 | 155.04 |
| Percent change | 18 | 16 | 20 | 22 | 23 | |
Lane Closure on Route B—Two Lanes Merging with Two Lanes
Traffic demands were varied on route A from 4,200 to 6,600 vehicles/h in increments of 300 vehicles/h and on route B from 1,000 to 2,400 vehicles/h in increments of 200 vehicles/h. Results in table 16 indicate negative (or insignificant) effects of DMC when route A traffic demands were 3,600 vehicles/h or less. A possible reason could be that the total volume of routes A and B did not exceed merge area capacity. When combined volumes exceeded 5,600 vehicles/h and route A demand exceeded 3,600 vehicles/h, DMC may improve operations. For the two lanes by two lanes case, the delay difference tended to show improvements only for mainline demands above 3,600 vehicles/h. The most significant gains were when both mainline and on-ramp demands were close to their capacities in optimal conditions.
| Route B Demand (vehicles/h) | Experimental Result | Route A Demand (vehicles/h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 3,000 | 3,200 | 3,400 | 3,600 | 3,800 | 4,000 | 4,200 | 4,400 | ||
| 1,000 | AVD (s) | -0.12 | -0.09 | -0.07 | -0.02 | 0.02 | 0.13 | 0.30 | 1.94 |
| Percent change | -2 | -1 | -1 | 0 | 0 | 1 | 3 | 14 | |
| 1,200 | AVD (s) | -0.18 | -0.12 | -0.08 | -0.01 | 0.18 | 0.22 | 2.27 | 7.01 |
| Percent change | -3 | -2 | -1 | 0 | 2 | 2 | 17 | 36 | |
| 1,400 | AVD (s) | -0.22 | -0.16 | -0.11 | -0.04 | 0.21 | 0.59 | 4.35 | 34.36 |
| Percent change | -3 | -2 | -1 | 0 | 2 | 5 | 27 | 72 | |
| 1,600 | AVD (s) | -0.28 | -0.20 | -0.03 | 0.12 | 0.55 | 2.17 | 17.90 | 109.07 |
| Percent change | -4 | -3 | 0 | 1 | 5 | 17 | 60 | 87 | |
| 1,800 | AVD (s) | -0.40 | -0.26 | -0.16 | 0.34 | 1.37 | 8.42 | 73.31 | 195.07 |
| Percent change | -5 | -3 | -2 | 3 | 12 | 42 | 83 | 87 | |
| 2,000 | AVD (s) | -0.65 | -0.52 | -0.13 | 0.70 | 3.94 | 28.09 | 139.57 | 202.11 |
| Percent change | -8 | -6 | -1 | 6 | 26 | 67 | 85 | 68 | |
| 2,200 | AVD (s) | -1.49 | -1.18 | -0.47 | 0.97 | 8.38 | 57.93 | 151.97 | 177.24 |
| Percent change | -17 | -12 | -4 | 7 | 37 | 71 | 70 | 50 | |
| 2,400 | AVD (s) | -9.54 | -13.40 | -12.50 | -21.55 | -26.56 | 29.53 | 95.95 | 106.44 |
| Percent change | -100 | -123 | -100 | -125 | -70 | 22 | 34 | 26 | |
It should be noted that ramp metering effects may be comparable to DMC in terms of managing ramp volumes and downstream mainline volumes. One-lane on-ramps merging into two-, three-, and four-lane freeways were investigated. Considering the complexity of signal-controlled on-ramp traffic, the current research is limited to continuous on-ramp traffic. The major differences for the on-ramp merge study herein are as follows:
One-Lane Ramp Merging with Two-Lane Freeway
Traffic demands were varied on the mainline from 1,000 to 2,400 vehicles/h in increments of 200 vehicles/h and on route B from 1,000 to 2,000 vehicles/h in increments of 200 vehicles/h. Paired t-tests indicate that the AVD differences for all considered traffic demands were statistically significant at the 95 percent confidence interval. Table 17 indicates that when either mainline or ramp traffic demands were lower than 1,400 vehicles/h, closing a mainline lane did not have clear effects on network performance regardless of demand on the on-ramp. This is reasonable because with 1,400 vehicles/h or less on the mainline, on-ramp demands between 1,000 and 2,000 vehicles/h would not exceed merge area capacity. Moreover, traffic from either road would not interact very much in the merge area. Results also show that closing a mainline lane would not benefit network performance until total demands exceeded 3,600 vehicles/h.
| Route B Demand (vehicles/h) | Experimental Result | Route A Demand (vehicles/h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1,000 | 1,200 | 1,400 | 1,600 | 1,800 | 2,000 | 2,200 | 2,400 | ||
| 1,000 | AVD (s) | 0.44 | 0.46 | 0.59 | 0.8 | 0.79 | 0.86 | 0.62 | -13.73 |
| Percent change | 7 | 7 | 8 | 9 | 8 | 8 | 5 | -88 | |
| 1,200 | AVD (s) | 0.54 | 0.66 | 0.74 | 1 | 1.47 | 2.42 | 4.28 | -5.74 |
| Percent change | 8 | 9 | 9 | 11 | 14 | 19 | 26 | -24 | |
| 1,400 | AVD (s) | 0.59 | 0.75 | 1.06 | 1.44 | 2.39 | 5.43 | 12.32 | 10.86 |
| Percent change | 8 | 9 | 12 | 14 | 20 | 33 | 49 | 28 | |
| 1,600 | AVD (s) | 0.68 | 0.86 | 1.22 | 2.2 | 5.15 | 13.97 | 19.28 | 35.97 |
| Percent change | 8 | 10 | 12 | 19 | 33 | 55 | 59 | 56 | |
| 1,800 | AVD (s) | 0.75 | 0.94 | 1.44 | 4.1 | 8.85 | 19.33 | 34.6 | 44.57 |
| Percent change | 8 | 10 | 13 | 29 | 44 | 61 | 71 | 61 | |
| 2,000 | AVD (s) | 0.75 | 0.98 | 1.9 | 6.56 | 12.93 | 21.46 | 35.77 | 53.78 |
| Percent change | 8 | 10 | 16 | 39 | 54 | 64 | 72 | 66 | |
One-Lane Ramp Merging with Three-Lane Freeway
Traffic demands on route A were varied from 2,100 to 4,800 vehicles/h in increments of 300 vehicles/h and on route B from 1,000 to 2,000 vehicles/h in increments of 200 vehicles/h. The reason for the maximum 2,000 vehicles/h was because the on-ramp traffic was controlled by surface signals where capacity rarely exceeded 2,000 vehicles/lane. Paired t-tests show that reductions of AVD were statistically significant at the 95 percent confidence interval for all tested traffic demand combinations. Table 18 shows that the DMC control could save each vehicle as much as 89 s (88 percent).
| Route B Demand (vehicles/h) | Experimental Result | Route A Demand (vehicles/h) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2,100 | 2,400 | 2,700 | 3,000 | 3,300 | 3,600 | 3,900 | 4,200 | 4,500 | 4,800 | ||
| 1,000 | AVD (s) | 0.68 | 1.09 | 1.45 | 2.47 | 5.20 | 9.41 | 12.20 | 13.14 | 15.45 | 24.25 |
| Percent change | +17 | +22 | +24 | +33 | +48 | +59 | +63 | +62 | +63 | +68 | |
| 1,200 | AVD (s) | 1.09 | 1.74 | 3.33 | 6.89 | 10.85 | 12.15 | 13.99 | 15.07 | 21.38 | 55.17 |
| Percent change | +23 | +29 | +41 | +56 | +64 | +65 | +65 | +65 | +70 | +83 | |
| 1,400 | AVD (s) | 1.65 | 3.16 | 7.20 | 11.34 | 12.72 | 13.65 | 15.36 | 19.07 | 32.09 | 86.23 |
| Percent change | +29 | +41 | +58 | +67 | +67 | +66 | +66 | +69 | +77 | +88 | |
| 1,600 | AVD (s) | 3.56 | 6.63 | 10.79 | 13.31 | 13.41 | 14.93 | 17.60 | 26.89 | 44.55 | 89.00 |
| Percent change | +44 | +57 | +66 | +68 | +67 | +67 | +68 | +75 | +82 | +88 | |
| 1,800 | AVD (s) | 5.32 | 10.96 | 12.27 | 13.90 | 14.56 | 16.18 | 21.97 | 31.67 | 47.28 | 87.55 |
| Percent change | +51 | +67 | +67 | +68 | +67 | +67 | +72 | +77 | +82 | +87 | |
| 2,000 | AVD (s) | 8.34 | 13.16 | 14.00 | 13.93 | 15.05 | 17.72 | 22.88 | 32.91 | 44.33 | 84.62 |
| Percent change | +62 | +70 | +70 | +68 | +67 | +69 | +72 | +77 | +81 | +87 | |
One-Lane Ramp Merging with Four-Lane Freeway
Traffic demands on route A were varied from 5,000 to 6,200 vehicles/h in increments of 400 vehicles/h and from 6,300 to 6,800 in increments of 100 vehicles/h. Demands on route B were varied from 1,200 to 1,800 vehicles/h in increments of 200 vehicles/h and from 1,900 to 2,200 vehicles/h in increments of 100 vehicles/h. The grid density was changed to perform detailed analysis on conditions near capacity. Table 19 shows DMC benefits under nearly all demand combinations. Vehicle delay savings can be as high as 95 percent.
| Route B Demand (vehicles/h) | Experimental Result | Route A Demand (vehicles/h) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5,000 | 5,400 | 5,800 | 6,200 | 6,300 | 6,400 | 6,500 | 6,600 | 6,700 | 6,800 | ||
| 1,200 | AVD (s) | 10.9 | 12.0 | 12.3 | 15.00 | 16.36 | 17.39 | 19.75 | 22.87 | 32.81 | 53.17 |
| Percent change | 59 | 59 | 57 | 59 | 61 | 61 | 64 | 67 | 73 | 81 | |
| 1,400 | AVD (s) | 11.8 | 13.2 | 14.2 | 18.42 | 22.97 | 31.14 | 36.96 | 48.44 | 84.55 | 113.3 |
| Percent change | 60 | 60 | 60 | 63 | 68 | 74 | 76 | 80 | 87 | 90 | |
| 1,600 | AVD (s) | 12.4 | 13.4 | 16.2 | 29.26 | 42.19 | 52.11 | 86.80 | 118.8 | 191.5 | 228.5 |
| Percent change | 60 | 60 | 62 | 73 | 79 | 82 | 88 | 91 | 94 | 95 | |
| 1,800 | AVD (s) | 13.5 | 14.9 | 21.5 | 62.94 | 99.75 | 146.4 | 186.7 | 218.9 | 267.4 | 333.7 |
| Percent change | 58 | 58 | 65 | 83 | 89 | 92 | 93 | 94 | 95 | 96 | |
| 1,900 | AVD (s) | 14.0 | 15.7 | 28.0 | 110.2 | 151.6 | 190.3 | 235.7 | 290.7 | 327.4 | 373.6 |
| Percent change | 50 | 52 | 65 | 87 | 90 | 92 | 93 | 94 | 95 | 95 | |
| 2,000 | AVD (s) | 14.3 | 18.2 | 48.6 | 141.1 | 172.6 | 235.2 | 265.4 | 308.8 | 363.2 | 397.9 |
| Percent change | 25 | 30 | 54 | 77 | 81 | 85 | 87 | 88 | 90 | 91 | |
| 2,100 | AVD (s) | 14.2 | 18.9 | 37.3 | 142.6 | 173.3 | 217.8 | 258.4 | 309.9 | 342.8 | 407.9 |
| Percent change | 12 | 16 | 28 | 61 | 66 | 71 | 74 | 78 | 80 | 82 | |
| 2,200 | AVD (s) | 13.3 | 17.5 | 42.9 | 133.8 | 179.5 | 214.8 | 263.1 | 310.2 | 345.4 | 395.4 |
| Percent change | 7 | 10 | 22 | 48 | 55 | 60 | 65 | 69 | 71 | 74 | |
In the scenarios, DMC benefits were sensitive to the combination of merging demand volumes and number of merging lanes. Under certain volume combinations, DMC control produced no benefit. Under other volume combinations, DMC control produced medium-to-high benefits. Therefore, it seems that a B/C analysis of DMC should at least evaluate the best-case scenarios while keeping in mind that only the “best” volume combinations would achieve those benefits. The best-case scenarios can be summarized as follows:
In the prior scenarios, route B vehicles experienced the most benefit, whereas route A vehicles remained mostly unaffected. For the three-lane merge with two-lane freeway (lane closure at ramp) scenario, average delay decreased by 100 s for 2,000 vehicles/h on route B. If 2,000 vehicles save an average of 100 s due to DMC treatment, total hourly time savings would be 55.56 vehicle-h, as shown in figure 59.
![]()
Figure 59. Equation. Total hourly time savings for the DMC example.
Assuming the same $17/h from the DLG B/C analysis, total daily cost savings would be $945, as shown in figure 60.
![]()
Figure 60. Equation. Total daily time savings for the DMC example.
For one-way freeways, it seems appropriate to assume DMC cost savings would only materialize during one peak period per day. If the number of commuting days per year is derived by excluding weekends and holidays, then the annual cost savings attributed to DMC could be $236,130 per year, as shown in figure 61.
![]()
Figure 61. Equation. Annual cost savings for the DMC example.
Applying similar cost calculations to all four scenarios yields the following best-case results:
These annual benefits could be compared against implementation costs, including the cost of installing and maintaining a DMS on the freeway. It could also include the engineering analysis costs of screening the volume combinations (to identify candidate merge areas) plus law enforcement (if any) for the new lane use. Engineering analysis would be critical because the above cost savings would only materialize under certain demand volumes.
Regarding the cost of installing and maintaining a DMS, the USDOT’s Knowledge Resources Web site implies the costs vary widely from $10,000 to $200,000.(52) Freeway DMS prices would likely be on the high end of this range, and a DMS tower (approximately $100,000) could also be required. Ideally, lifecycle maintenance and operation costs for the DMS would also be considered. A search for “DMC price” on the FHWA Web site leads to the information, from the USDOT ITS Benefits, Costs and Lessons Learned Database shown in table 9.
The 2014 Greater Richmond Safety and Mobility Study predicted $83,000 annual benefits from improved safety and $341,000 total annual costs for the I-64 corridor in Richmond, VA. The improved safety was due to fewer merging conflicts, producing an estimated 12 to 36 percent reduction in crashes. The annual costs included a lane control system, DMSs, and vehicle detection. Earlier it was stated that annual benefits could range from $236,000 to $1,002,000. VDOT assumes a 15-year lifespan for DMS signs. Assuming a total capital cost of $250,000, anticipated useful life of 15 years, and annual O&M costs of $6,000 per year, average annual cost and average annual benefits would be as follows:
These are mobility-based B/C ratios not accounting for safety and environmental impacts.
Dynamic and/or time-of-day lane closures on freeways are typically indicated by overhead DMSs. For DMC, the DMS are nominally positioned upstream of the merge gore. Decision sight distances could be obtained from the American Association of State Highway and Transportation Officials (AASHTO) and are sensitive to freeway design speeds.(62) This allows mainline drivers sufficient time and distance in which to vacate the rightmost merging lane. An example of DMSs used for DMC is shown in figure 48. DMSs are located downstream of the merge gore in this figure, but upstream DMSs (which cause mainline drivers to vacate the rightmost merging lane) are a higher priority. If the DMC is implemented in a predictable time-of-day fashion, static regulatory signs should be used to show hours of operation. Driver compliance could conceivably be improved by an automated gate, as illustrated in figure 62 and figure 63, similar to what is used when closing high-occupancy vehicle (HOV) lane entrances during off-peak periods. This option could improve on-ramp merge operations by completely emptying the rightmost mainline lane. However, there would be a possibility of mainline drivers occasionally stopping at the gate if they were unable to change lanes on time.
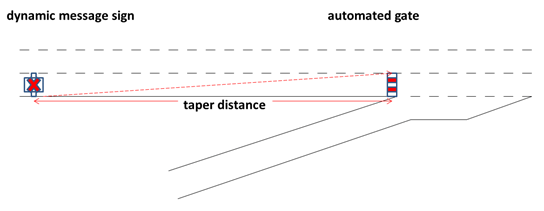
Figure 62. Illustration. Automated gate option for DMC.

Figure 63. Photo. Real-world image of an automated gate.(24)
The authors of this report investigated performance of the DMC strategy on a hypothetical road geometry involving a two-lane freeway merging with a two-lane freeway and dropping into four lanes. Traffic demands were varied on the minor road from 3,000 to 4,600 vehicles/h in increments of 200 vehicles/h and on the major road from 2,500 to 4,600 vehicles/h in increments of 300 vehicles/h for a total of 72 demand combinations. The major findings can be summarized as follows:
It is worthy to mention that a statistically significant improvement does not necessarily mean it is meaningful for practice. Agencies may set up their own criteria (e.g., average delay reduction of 10 percent or more) for justifying DMC implementation.
On freeways, merging at the terminus of an acceleration lane often causes a severe traffic bottleneck. Acceleration lane lengths shorter than or equal to those recommended by AASHTO guidelines were tested to quantify delay changes when freeways of less-than-ideal design were upgraded.(62) In the Paramics™ simulations, a parallel design (see figure 64) consisting of acceleration lane length (see figure 65) and taper lane length was used. For a typical three-lane corridor, it was found that, on average, increasing acceleration lane length from 500 to 1,000 ft reduced delay by 14 percent, while increasing length from 1,000 to 1,500 ft (close to AASHTO recommendations) reduced delay by an additional 9 percent. Results were similar on a four-lane corridor with a parallel acceleration lane.

Figure 64. Illustration. Acceleration lane length schematic (three-lane configuration).
Figure 65. Illustration. Acceleration lane geometry.
In total, 12 geometric configurations were modeled (see table 20). Each of the geometric configurations was simulated under nine different demand scenarios (see table 21 and table 22). Based on engineering judgment, base condition demands were chosen to produce moderate congestion that would not extend beyond 1 mi upstream of the merge section. Specifically, two mainline configurations (three and four lanes), three acceleration lane lengths (500, 1,000, and 1,500 ft), and two ramp speeds were tested. In most cases, acceleration lengths were shorter than or approximately equal to recommended design lengths under AASHTO guidelines (i.e., exhibit 10-70 in the 2004 manual or table 10-3 in the 2011 manual) and are shown in the last column on table 20.(63,62)
All tabular simulation results shown were derived by aggregating detector readings. These detectors were placed at 500-ft intervals along the merge section and up to 1 mi upstream of the merge section to fully capture the spatial and temporal extent of delays. Detectors were also placed on the on-ramp at 500-ft intervals to capture on-ramp delays. Average speeds reported along the 1-mi corridor reflect average conditions up to 1 mi upstream of the merge section.
| Configuration Number |
Number of TH Lanes | Ramp Speed (mi/h) |
Acceleration Length (ft) |
Acceleration Length from the 2011 AASHTO Guideline(39) (ft) |
|---|---|---|---|---|
| 1 | 3 | 40 | 500 | 780 + 300 taper |
| 2 | 3 | 40 | 1,000 | 780 + 300 taper |
| 3 | 3 | 40 | 1,500 | 780 + 300 taper |
| 4 | 3 | 30 | 500 | 1,160 + 300 taper |
| 5 | 3 | 30 | 1,000 | 1,160 + 300 taper |
| 6 | 3 | 30 | 1,500 | 1,160 + 300 taper |
| 7 | 4 | 40 | 500 | 780 + 300 taper |
| 8 | 4 | 40 | 1,000 | 780 + 300 taper |
| 9 | 4 | 40 | 1,500 | 780 + 300 taper |
| 10 | 4 | 30 | 500 | 1,160 + 300 taper |
| 11 | 4 | 30 | 1,000 | 1,160 + 300 taper |
| 12 | 4 | 30 | 1,500 | 1,160 + 300 taper |
Table 21 and table 22 present desired demands for each scenario under the three- and four-lane freeway configurations. The combination of geometric and demand scenarios presented in table 20 through table 22 resulted in 216 scenarios. Each scenario was run 10 times, and the average results are presented. Each geometric configuration was simulated with nine demand scenarios. On-ramp demands ranged from 578 to 1,978 vehicles/h/lane in the three-lane configuration and from 1,278 to 1,678 vehicles/h/lane in the four-lane configuration.
| Demand Scenario | TH Demand (vehicles/h) |
On Ramp Demand (vehicles/h) |
|---|---|---|
| 1 | 4,847 | 1,278 |
| 2 | 5,047 | 1,278 |
| 3 | 5,547 | 778 |
| 4 | 4,147 | 1,578 |
| 5 | 3,547 | 1,978 |
| 6 | 5,797 | 578 |
| 7 | 5,347 | 1,078 |
| 8 | 4,547 | 1,428 |
| 9 | 4,047 | 1,678 |
| Demand Scenario | TH Demand (vehicles/h) |
On Ramp Demand (vehicles/h) |
|---|---|---|
| 10 | 5,347 | 1,278 |
| 11 | 5,647 | 1,278 |
| 12 | 6,147 | 1,278 |
| 13 | 5,347 | 1,478 |
| 14 | 5,347 | 1,678 |
| 15 | 5,647 | 1,478 |
| 16 | 5,647 | 1,678 |
| 17 | 6,147 | 1,478 |
| 18 | 6,147 | 1,678 |
Figure 66 through figure 69 present total delay for each of the nine demand scenarios and for three different lane configurations. The red, green, and purple lines represent total delay for the 500-, 1,000-, and 1,500-ft acceleration lane lengths, respectively. As expected, the purple line (representing 1,500 ft) corresponds to the minimum amount of delay and has the lowest Y-coordinates. Where lines intersect, it means delays for different lane lengths were similar. This happens in simulations for demand scenarios 3 and 6, which had relatively low ramp volumes (below 800 vehicles/h/lane). For these two scenarios, the combination of ramp and mainline flow implies that increasing the acceleration length did not yield any reductions in delay.
The three-lane 40 mi/h configuration findings are as follows:
The three-lane 30 mi/h configuration findings are as follows:
The four-lane 40 mi/h configuration findings are as follows:
The four-lane 30 mi/h configuration findings are as follows:
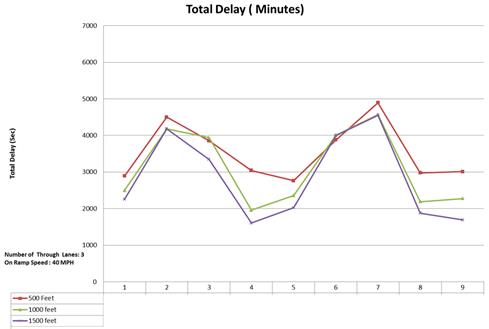
Figure 66. Graph. Total delay for three mainline lanes and 40-mi/h ramp speed.
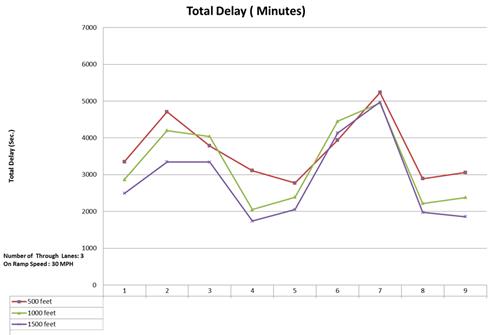
Figure 67. Graph. Total delay for three mainline lanes and 30-mi/h ramp speed.
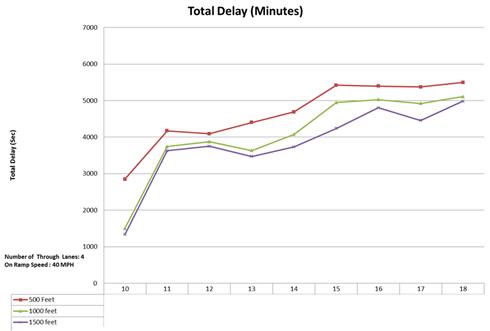
Figure 68. Graph. Total delay for four mainline lanes and 40-mi/h ramp speed.
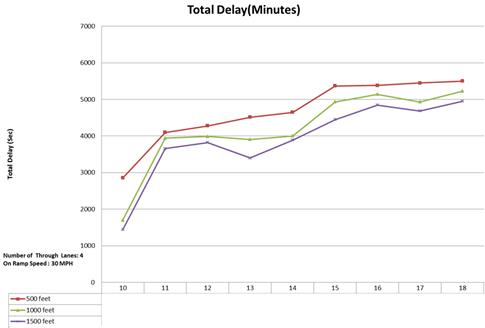
Figure 69. Graph. Total delay for four mainline lanes and 30-mi/h ramp speed.
According to the result tables, increasing acceleration lane length from 500 to 1,000 ft would save at least 395 min (i.e., 6.58 h) per day for the three-lane 40 mi/h configuration. Although additional vehicles beyond those simulated would likely benefit throughout the day, a conservative analysis can assume monetary benefits occur during the study period only. Assuming the same $17 per hour from the DLG B/C analysis, total daily cost savings would be $112, as shown in figure 70.
![]()
Figure 70. Equation. Total daily time savings for extended acceleration lanes.
Adjusting for the number of commuting days, annual cost savings could be $27,965 per year, as shown in figure 71.
![]()
Figure 71. Equation. Annual cost savings for extended acceleration lanes.
Increasing the acceleration lane length from 500 to 1,500 ft was shown to save 635 min (i.e., 10.58 h) per day, so this annual cost savings could increase to $44,965.
Table 23 illustrates the estimated cost savings for various scenarios.
| Scenario | Estimated Annual Cost Savings | |
|---|---|---|
| 1,000-ft Acceleration Lane Length | 1,500-ft Acceleration Lane Length | |
| Three lanes, 40 mi/h | $27,965 | $44,965 |
| Three lanes, 30 mi/h | $34,354 | $61,058 |
| Four lanes, 40 mi/h | $43,562 | $67,717 |
| Four lanes, 30 mi/h | $42,712 | $78,838 |
Annual benefits between $45,000 and $79,000 for increasing from 500 to 1,500 ft, could be compared against construction costs. In addition, greater savings would be expected in scenarios of on-ramp flow exceeding 1400 vehicles/h/lane. According to TTI’s mobility investment priorities, incorporating acceleration lanes by simple shoulder conversion can cost between $50,000 and $100,000 but can cost over $1 million for complex retrofits.(64,65) However, in 2013–2014, Arlington, TX, spent $640,000 to extend the Lamar Boulevard entrance ramp/acceleration lane on WB IH-30.(66)
The lifespan of a 1,000-ft acceleration lane area is uncertain but is expected to exceed the 15-year lifespan of DMSs. This analysis (1,000 ft added to the acceleration lane) assumes a useful life of 30 years and annual O&M costs of $1,200 per year.
When combining the worst-case benefits ($45,000 per year) with the worst-case costs ($34,500 per year), the B/C ratio of 13:10 implies that expected savings would exceed implementation costs by only 30 percent. However when combining the best-case benefits ($79,000 per year) with the best-case costs ($2,900 per year), the B/C ratio is 28:1. These are mobility-based B/C ratios not accounting for safety and environmental impacts.
The use of limited HSR for merge control when the complete hard shoulder lane is not opened for general traffic usage has the potential to provide better merge section operations. HSR requires extensive monitoring, servicing, maintenance, and incident reaction, as discussed in the B/C Analysis section. This section describes a number of HSR scenarios, which were studied by using the ParamicsTM simulation software. HSR benefits were documented in terms of delay reductions. Results indicated delay reductions between 9 and 20 percent, depending on demand level, and propensity of drivers to use the HSR lane. This implies that agencies should consider dynamic use of hard shoulders for better merge performance without opening up the entire hard shoulder for general traffic usage. Figure 72 shows a schematic of the HSR configuration on I-80 between Atlantic Avenue and Douglas Boulevard in Roseville, CA.
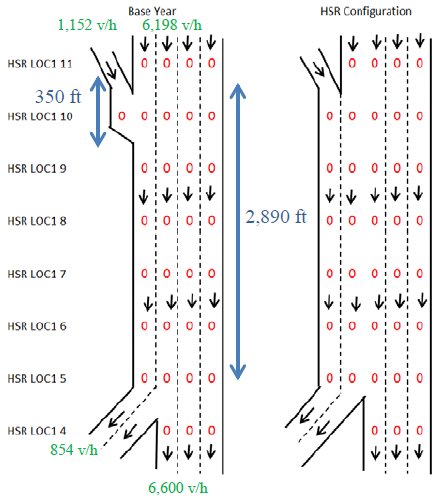
Figure 72. Illustration. HSR strategy schematic.
A series of scenarios were run to test the factors influencing facility performance. These factors include the following:
In total, 12 scenarios were analyzed: 4 with regular demand, 4 with low demand (95 percent of the regular demand), and 4 with high demand (105 percent of the regular). In table 24, non-HSR scenarios are bolded for easier comparison. Alternative scenarios were constructed by varying speed limit between 45 and 55 mi/h and by prohibiting 50 percent of drivers from entering the HSR lane, a scenario called “reduced likelihood of HSR use.”
In the model, all delays and speeds were reported for the hourly period between 7:30 and 8:30 a.m. Delay and speed calculations were based on detectors spaced at 500-ft intervals along a 1-mi-long corridor. Findings are as follows:
| Simulation Number | Demand | HSR Type | Total Delays (min) |
Average Speed (mi/h) |
On-Ramp Volume (vehicles/h) |
Upstream Volume (vehicles/h) |
Downstream Volume (vehicles/h) |
|---|---|---|---|---|---|---|---|
| 1 | Base | No HSR | 8,186 | 35.0 | 1,156 | 6,902 | 7,380 |
| 2 | Base | 55 mi/h HSR lane | 6,522 | 39.4 | 1,159 | 6,889 | 7,369 |
| 3 | Base | 45 mi/h HSR lane | 6,725 | 38.7 | 1,158 | 6,893 | 7,369 |
| 4 | Base | Reduced likelihood of HSR use | 7,081 | 37.8 | 1,156 | 6,904 | 7,381 |
| 5 | Low | No HSR | 5,779 | 40.8 | 1,072 | 6,560 | 7,012 |
| 6 | Low | 55 mi/h HSR lane | 4,652 | 44.9 | 1,068 | 6,553 | 7,034 |
| 7 | Low | 45 mi/h HSR lane | 4,677 | 44.8 | 1,069 | 6,549 | 7,033 |
| 8 | Low | Reduced likelihood of HSR use | 5,293 | 42.5 | 1,066 | 6,567 | 7,021 |
| 9 | High | No HSR | 13,492 | 27.6 | 1,217 | 7,146 | 7,633 |
| 10 | High | 55 mi/h HSR lane | 11,948 | 28.3 | 1,225 | 7,105 | 7,638 |
| 11 | High | 45 mi/h HSR lane | 12,187 | 28.0 | 1,226 | 7,126 | 7,640 |
| 12 | High | Reduced likelihood of HSR use | 11,526 | 29.2 | 1,221 | 7,185 | 7,695 |
| Note: Bolded text indicates base case condition (without HSR). | |||||||
| HSR Type | Base | Low Demand | High Demand | |||
|---|---|---|---|---|---|---|
| Total Delay (min) | Difference from No HSR (percent) | Total Delay (min) | Difference from No HSR (percent) | Total Delay (min) | Difference from No HSR (percent) | |
| No HSR | 8,186 | 0 | 5,779 | 0 | 13,492 | 0 |
| 55-mi/h HSR lane | 6,522 | -20.3 | 4,652 | -19.5 | 11,948 | -11.4 |
| 45-mi/h HSR lane | 6,725 | -17.8 | 4,677 | -19.1 | 12,187 | -9.7 |
| Reduced likelihood of HSR use | 7,081 | -13.5 | 5,293 | -8.4 | 11,526 | -14.6 |
Table 26 illustrates the possible cost savings from HSR based on delay reductions from table 25. These savings assume the same $17/h and 250 commuting days per year from the DLG B/C analysis. These savings also assume 3 h of HSR benefits per day.
| Simulation Number | Demand | HSR Type | Total Delay (h) |
Annual Savings (dollars) |
|---|---|---|---|---|
| 1 | Base | No HSR | 136.4 | 0 |
| 2 | Base | 55 mi/h HSR lane | 108.7 | 353,100 |
| 3 | Base | 45 mi/h HSR lane | 112.1 | 309,900 |
| 4 | Base | Reduced likelihood of HSR use | 118.0 | 234,600 |
| 5 | Low | No HSR | 96.3 | 0 |
| 6 | Low | 55 mi/h HSR lane | 77.5 | 239,700 |
| 7 | Low | 45 mi/h HSR lane | 78.0 | 233,400 |
| 8 | Low | Reduced likelihood of HSR use | 88.2 | 103,200 |
| 9 | High | No HSR | 224.9 | 0 |
| 10 | High | 55 mi/h HSR lane | 199.1 | 329,100 |
| 11 | High | 45 mi/h HSR lane | 203.1 | 278,100 |
| 12 | High | Reduced likelihood of HSR use | 192.1 | 418,200 |
These annual benefits would presumably be compared against construction and maintenance costs. Opening hard shoulders for limited times of operation often requires a DMS. During the earlier B/C analysis for DMC, it was seen that freeway DMS costs can exceed $200,000. Moreover, HSR requires extensive monitoring, servicing, maintenance, and incident reaction.(67) An extensive camera system is recommended “to ensure the shoulder is clear prior to opening.”(67) Increased monitoring tends to bring increased service and maintenance costs. Finally, hard shoulder use by passenger cars adds new challenges for incident response. HSR could potentially add new costs associated with managing such incidents and controlling emergency vehicle access. The use of emergency pullouts at half-mile spacings is encouraged to provide refuge areas that could accommodate many of the disabled situations. Some areas have invested in service patrols, staged tow trucks, and other traffic incident management enhancements.
According to the Texas A&M toolbox for adding capacity, converting a shoulder to a shoulder lane costs $1.5 million for construction plus engineering and $12,000 per year for maintenance.(68) The toolbox further projects a B/C ratio of roughly 7:1.
The lifespan of a hard shoulder is uncertain, but this analysis assumed a useful life of 30 years. When combining the worst-case benefits under low demand volumes ($103,000 each year) with the worst-case costs ($1.5 million start-up and $12,000 annual maintenance), the B/C ratio of 1.7:1 implies that benefits would exceed costs by only 70 percent. However, when combining the best-case benefits under high demand volumes ($418,000 each year) with the best-case costs ($250,000 start-up and $6,000 annual maintenance), the B/C ratio is a much more favorable 29:1. These are mobility-based B/C ratios not accounting for safety and environmental impacts.
In congested freeways with four lanes or more, reducing lane widths to 10 ft can create space for an additional lane. This can often be done without any construction or requisition of additional space. According to simulation results, the additional capacity obtained by adding a lane was effective at offsetting the reduced speeds caused by narrow lanes, eliminating bottlenecks, and producing higher corridor speeds. Specifically, reducing lane widths from 12 to 10 ft on the four-lane corridor and adding an additional 10-ft lane reduced overall corridor delay by 21 percent. Real-world implementations of 10-ft freeway lanes have occurred in California and Hawaii, as discussed later in the B/C Analysis section. Other reduced-width (11-ft) lanes were created on the I-75 and I-85 corridors in Georgia inside the I-285 perimeter. They were installed in combination with requirements that through trucks must bypass downtown Atlanta, GA, by using I-285. To assess operational benefits, a four-lane freeway segment was selected in Buffalo NY. This is four-lane facility has frequent on- and off-ramps whose mainline width is 48 ft (4 by 12 ft). The base year configuration was extended to four lanes along segments in which the roadway dropped to three lanes. In the base scenario shown in figure 73, a primary source of congestion was the friction caused by vehicles using various freeway ramps (I-290), especially near the on- and off-ramps (e.g., detector location 175 in figure 73).
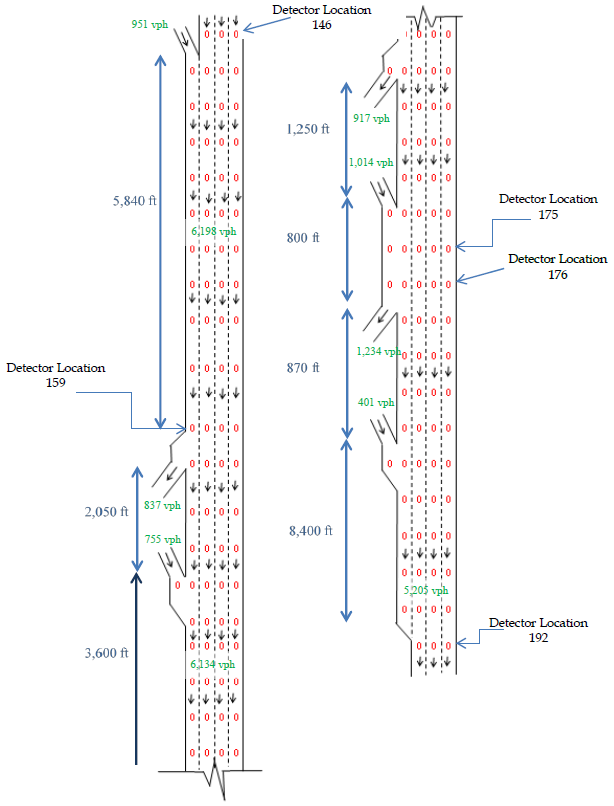
Figure 73. Illustration. Base year analysis of reducing lane widths to add new lanes.
As shown in figure 74, adding a fifth new lane and then reducing all lane widths to 10 ft ensured that the total roadway width differed only by 2 ft (48 versus 50 ft). It has been observed and documented in the 2010 HCM that drivers reduce their speed when driving on lanes narrower than 12 ft.(6) Specifically, it is expected that drivers reduce their speed by an average of 7 mi/h when driving on a 10-ft lane (see figure 75). Results indicate that speed reductions caused by lane-narrowing were offset by the additional capacity produced by an additional lane. These results are summarized in table 27 and table 28. In addition to the reduced lane-width scenarios, researchers also modeled a five-lane freeway with 12-ft lane widths to investigate the impact of building additional roadway as opposed to redistributing the existing roadway. In this experiment, demand was loaded from 5:30 to 9 a.m., while simulation results were collected between 6 and 9 a.m. Detectors were placed at 500-ft intervals along the corridor’s 4.7-mi length to obtain speed and flow readings. Free-flow speed in the corridor was 70 mi/h.
Figure 74. Illustration. Equivalent freeway scenario with five mainline lanes.
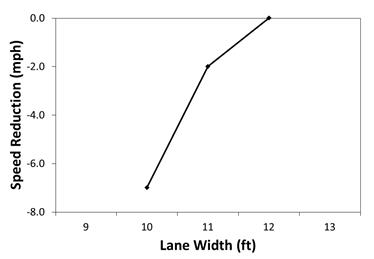
Figure 75. Graph. Speed reduction as a function of lane width.
| Scenario | Description | Total Delay from 6–9 a.m. (vehicle-min) |
Reduction from Base Percent |
|---|---|---|---|
| Base | Modified existing roadway | 50,715 | 0 |
| 1 | One additional 12-ft lane | 28,741 | 43 |
| 2 | One additional 12-ft lane plus a 20-min incident on lane 5 starting at 8 a.m. | 60,241 | -19 |
| 3 | One additional lane added by reducing all lane widths to 10 ft | 39,899 | 21 |
| 4 | One additional lane added by reducing all lane widths to 10 ft. A 30-min incident occurred on lanes 4 and 5 starting at 8 a.m. | 68,019 | -34 |
| Scenario | Mean Speed (mi/h) |
Upstream Volume (vehicles/h) |
Downstream Volume (vehicles/h) |
|---|---|---|---|
| Base | 41 | 17,274 | 16,814 |
| 1 | 50 | 17,880 | 16,810 |
| 2 | 39 | 17,564 | 16,520 |
| 3 | 46 | 17,821 | 16,893 |
| 4 | 36 | 17,627 | 16,384 |
Table 27 summarizes delay results from the ParamicsTM simulation environment, while table 28 summarizes the average speeds and throughput. The base year configuration was moderately congested, with an average speed of 41 mi/h between 6 and 9 a.m. Scenarios 1 and 2 involve maintaining existing lane widths and adding one more lane that is 12 ft wide to examine the benefits of new roadway capacity. In scenario 1, total vehicle delay dropped from 50,715 to 28,741 vehicle-min. This implies a 42 percent reduction in delay if one more 12-ft lane was constructed. Such reduction happens because the bottleneck from detector 176 to 159 in the base year was eliminated in scenario 1. A 30-min incident blocking the rightmost two lanes (4 and 5) resulted in 60,241 vehicle-min of delay (scenario 2), which is higher than the base year delay of 50,715 vehicle-min.
Scenarios 3 and 4 involved a five-lane freeway but with reduced lane widths that avoided any construction. Scenario 3 converted existing lanes to 10 ft and added a fifth lane, reducing delay to 39,899 vehicle-min. This is a 21 percent reduction, which is half the reduction obtained by adding new roadway capacity. For scenario 3, average speed over the 3-h period from 6 to 9 a.m. was 46 mi/h as opposed to 41 mi/h in the base year. However, speed contour plots (not shown) indicated that the scenario 3 speed was uniform, rarely dropping below 30 mi/h throughout most of the corridor. In fact, the main bottleneck along the corridor spanning from detector 156 to 176 disappeared. Although there were some low speeds at the end, these were due to capacity reductions outside the modeling area, and were carried over across all scenarios.
Scenario 4 copied the 10-ft configuration from scenario 3 and added a 30-min two-lane incident at 8 a.m. This increased delay from 39,899 vehicle-min in scenario 3 to 68,109 vehicle-min, a 41 percent increase. In both incident scenarios, delay was higher than the incident-free base year even though the incidents lasted for only 30 min. As expected, an incident on the 10-ft freeway (scenario 4) had a greater delay than the same incident on a 12-ft freeway (scenario 2). Table 28 contains information on the mean corridor speed and on volumes upstream and downstream of the simulation corridor (detectors 146 and 192 in figure 73).
According to the simulation results, increasing the number of lanes from four to five lanes (with narrower lane widths) would save 39,899 min (i.e., 665 h) during the 3-hour peak travel period. Although additional time savings would likely occur throughout the day, a conservative analysis can assume monetary benefits occur during the 3-hour peak period only. Assuming the same $17 per hour and 250 commuting days from the DLG B/C analysis, annual cost savings would be $2.83 million.
Cost information on restriping all mainline lanes to create a new lane without actually building a new lane has been relatively difficult to locate. Moreover, the cost of rerouting traffic is unclear. Unlike the other bottleneck mitigation strategies, lane narrowing for the purpose of adding a lane would require diverting each mainline lane at some point, causing greater congestion costs during construction. The Honolulu Star Advertiser cited a $200,000 project in 2012 to add a fourth lane on H-1 in Hawaii.(69) This restriping work was performed only during nighttime hours. However, in 1985, the Los Angeles Times predicted an $800,000 cost to increase lanes (via narrower lane widths) on a short section of Ventura Freeway.(70)
The lifespan of a fifth lane is uncertain, but this analysis assumed a useful life of 30 years. Assuming O&M costs of $6,000/year/lane-mi, and given that the Buffalo, NY, simulation took place over 22,810 ft (4.3 mi) as shown in figure 74, O&M costs were estimated at 6,000 × 4.3 = $25.9,000/year/lane-mi. Assuming construction and traffic diversion costs of $2 million, the estimated B/C ratio is 30:1. The average annual cost and average annual benefit are as follows:
This is a mobility-based B/C ratio not accounting for safety and environmental impacts.
In recent years, bottleneck mitigation has been attempted through strategies such as ramp metering and VSLs. This section presented research on the following five featured mitigation strategies, which are expected to be cost effective:
At arterial intersections, the travel demand may vary significantly by time, and the lane assignments, designed for the most severe peak hour traffic, might not suit these different demand patterns. DLG can reduce the gap between supply and demand by changing lane assignments dynamically. In the two case studies, DLG reduced overall intersection delay by up to 30 percent. Screening criteria can be changed to fit local agency needs. Estimated DLG B/C ratios ranged between 7:1 for low-volume intersections and 29:1 for high-volume intersections. These ratios also assume that DLG is only applied to intersections flagged as good candidates for DLG treatment according to the screening process.
Microscopic simulations of DMC of two-lane freeways merging with three-lane freeways and dropping into four lanes produced the following findings:
On freeways, merging at the terminus of an acceleration lane often caused a severe traffic bottleneck. In microscopic simulations of a typical three-lane corridor, increasing acceleration lane length from 500 to 1,000 ft reduced delay by 14 percent, while increasing the length from 1,000 to 1,500 ft (close to AASHTO recommendations) reduced delay by an additional 9 percent. Results were similar on a four-lane corridor with a parallel acceleration lane. When increasing to 1,500 ft, estimated B/C ratios ranged between 13:10 and 28:1. B/C ratios were less favorable when increasing to only 1,000 ft.
The use of limited HSR for merge control when the complete hard shoulder lane is not opened for general traffic usage has the potential to provide better merge section operations. Results indicated delay reductions between 9 and 20 percent depending on demand level and drivers’ propensity to use the HSR lane. This implies that agencies should consider dynamic use of hard shoulders for better merge performance without opening up the entire hard shoulder for general traffic usage. Under high-demand volumes, estimated B/C ratios ranged between 1.7:1 and 29:1. B/C ratios were less favorable under low demand volumes.
In congested freeways with four lanes or more, reducing lane widths to 10 ft can create the space needed to add an additional lane. This can often be done without any construction or requisition of additional space. According to simulation results, the additional capacity obtained by adding a lane was effective at offsetting the reduced speeds caused by narrow lanes, eliminating bottlenecks, and producing higher corridor speeds. Specifically, reducing lane widths from 12 to 10 ft on the four-lane corridor and adding an additional 10-ft lane reduced overall corridor delay by 21 percent. B/C ratios were estimated at 30:1.
In addition to the five featured strategies, the following alternative intersection and interchange designs are recommended:
For more information, refer to FHWA’s AIIR and Alternative Intersection Design Web site.(47)
Regarding the automated methods for CBI, further model enhancements are sought for modeling traffic speed with more weather information, including wind direction and speed. The model will be validated using other data sets from other roadways. Another future enhancement of the model is replacing the symmetric normal distributions with nonsymmetric distributions, such as log-normal or gamma distributions.
DLG aims to adjust lane assignment based on changing demand to further improve intersection capacity utilization. Future software tools should automatically forecast delay reductions and other improvements to the performance measures at all locations flagged as DLG candidates. If such tools were available, subsequent sensitivity analyses could theoretically determine optimal threshold values for the screening criteria.
DMC is one of the major DJC strategies. The research presented was constrained to a specific set of geometric and traffic conditions, and the study was solely based on simulation work. Although DMC has not been implemented in the United States, field experiments are desired to validate the proposed strategy. Moreover, the current study closed a lane approximately 1,000 ft upstream of the merge gore and informed drivers 2,500 ft upstream. The next phase of this study will investigate varying lane closing locations and varying distances to inform drivers. Furthermore, the current research assumes a 100 percent compliance ratio when closing a lane. In the next phase, various compliance ratios will be evaluated.
The simulation of mitigation strategies showed beneficial impacts for a limited set of geometries. Some of these analyses could be expanded to include different geometry and flow patterns. The nationwide bottleneck analyses have revealed geometries of some of the most representative and problematic merge, weave, or diverge sections. These problematic geometries could be examined in future research.
Another important subject to investigate is the impact of autonomous or semi-autonomous vehicles on traffic flow. Limited research on this topic in the last 5 years indicates a beneficial impact of even a small percentage of semi-autonomous vehicles on traffic flow. However, the impact of various cooperative and autonomous driving strategies should be thoroughly investigated to understand how much each strategy benefits individual vehicles and the traffic stream.
2 According to chapter 8 of the 2016 HCM, LOS can be used to communicate roadway performance to laypersons. For example, LOS A represents the best operating conditions from the traveler’s perspective, and LOS F represents the worst.(45)