CHAPTER 6. OPEN-ROAD STUDY
Toward the conclusion of the closed-course study, the researchers talked with city representatives and made requests during professional society meetings, seeking cities that would be willing to participate in the open-road research. Four cities volunteered: Milwaukee, WI; Flagstaff, AZ; Austin, TX; and College Station, TX. As a minimum, the cities were asked to identify at least two locations that allowed the treatments to be installed in one location and then rotated to the other location after the initial data collection. Table 161 lists the sites included in the study.
Table 161. Study site characteristics.
Site |
Posted speed limit (mi/h) |
Total crossing distance (ft) |
Crossing distance to refuge (ft) |
Calculated daily traffic (vehicles/day) |
Advance yield lines? |
Number of lanes |
Presence of median |
| AU-01 | 35 | 44 | 44 |
17,732 | No |
4 |
None |
| AU-02 | 30 | 56 | 22 |
9,096 | No |
3 |
Raised |
| CS-01 | 30 | 48 | 48 |
2,130 | No |
2 |
None |
| CS-02 | 40 | 60 | 60 |
16,496 | Yes |
4 |
TWLTL |
| FG-01 | 35 | 84 | 31.5 |
23,008 | No |
4 |
Raised |
| FG-02 | 30 | 55 | 21 |
19,297 | No |
2 |
Raised |
| FG-03 | 35 | 76 | 28.5 |
14,590 | No |
4 |
Raised |
| MK-04 | 30 | 39 | 39 |
7,238 | No |
2 |
None |
| MK-05 | 30 | 40 | 40 |
6,883 | No |
4 |
None |
| MK-06 | 30 | 80 | 31 |
13,312 | No |
4 |
Raised |
| MK-07 | 30 | 98 | 42 |
11,401 | No |
6 |
Raised |
| MK-08 | 30 | 49 | 49 |
10,117 | No |
4 |
None |
The calculated daily traffic (CDT) was determined based on 1-hour counts made from the video recordings. The values for hourly percentage of ADT were determined using hourly traffic distributions available in the 2011 Urban Mobility Report.(34) The distributions for non-freeway, a.m. and p.m. peak periods for both no/low congestion and moderate congestion were considered to obtain typical weekday values. These volume distributions were combined to generate an overall representative distribution for use in this project. Figure 75 shows the hourly distribution used to adjust the 1-h counts into CDT values. For example, the 1-h count at MK-05 was 382vehicles and was done from 11 a.m. to noon. That hour represents 5.55 percent of the daily traffic, so 382/0.0555 = 6,883 vehicles/day.
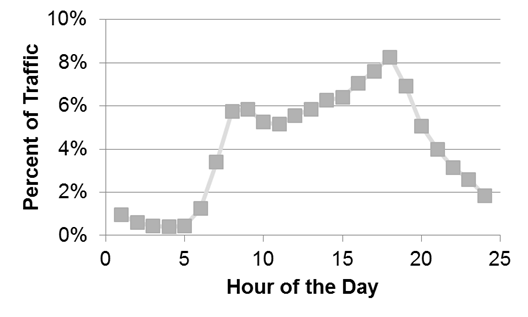
Figure 75. Graph. Typical hourly distribution used to convert 1-h volume into CDT.
Examples of the study assemblies are shown in figure 76 through figure 87. The beacons were mounted on a roadside pole to supplement a W11-2 (pedestrian) crossing warning sign with a diagonal downward arrow (W16-7P) plaque, and located at or immediately adjacent to a marked crosswalk. The RRFBs were mounted and operated as detailed in the FHWA Interim Approval and/or the subsequent official interpretations issued by FHWA on RRFB installations. The circular beacons used high-intensity LED-based indications (meeting Class 1 requirements), and used the rapid-flashing pattern used by the RRFB. The 12-inch circular beacons were mounted beneath the pedestrian crossing sign.
The flash pattern used at the sites was the 2-5 pattern currently used with the RRFBs. In the
2-5 pattern, one side of the beacon pulses twice followed by the other side pulsing five times. Table 162 provides information on installation order along with the dates of the data collection.
To account for the potential that device installation order could affect the results, the RRFB was installed first in some locations and second in other locations. For the 12 study sites, the RRFB was installed first in half of the sites while the CRFB was installed first in the other half of the sites.
Because preliminary findings from another closed-course study indicated that brightness of the beacons can influence how quickly a participant can detect a pedestrian within a crosswalk, efforts were made to measure the brightness of the beacons included in this study.(34) Because of limited funds, only one trip was made to each city to measure brightness. When knowledge was available regarding the new location of a measured beacon after rotation, the brightness level of that beacon in the new location was assumed to be the same as was measured in the previous location.

Figure 76. Photo. Rectangular beacons used at CS-01.

Figure 77. Photo. Circular beacons used at CS-02.

Figure 78. Photo. Circular beacons used at AU-01.

Figure 79. Photo. Rectangular beacons used at AU-02.

Figure 80. Photo. Circular beacons used at MK-04.

Figure 81. Photo. Circular beacons used at MK-05.

Figure 82. Photo. Circular beacons used at MK-06.

Figure 83. Photo. Rectangular beacons used at MK-07.

Figure 84. Photo. Rectangular beacons used at MK-08.

Figure 85. Photo. Circular beacons used at FG-01.

Figure 86. Photo. Circular beacons used at FG-02.

Figure 87. Photo. Rectangular beacons used at FG-03.
Table 162. Installation dates and dates of data collection.
| Site |
Existing beacon on assemblya |
Date of before data collection |
Initial assembly |
Date CRFB installed |
Date of CRFB data collection |
Date RRFB installed |
Date of RRFB data collection |
| AU-01 |
24/7 |
8/29/2013 |
CRFB |
2/3/2014 |
3/26/2014 |
4/10/2014 |
4/24/2014 |
| AU-02 |
Activated |
8/28/2013 |
RRFB |
4/10/2014 |
4/23/2014 |
3/7/2014 |
3/25/2014 |
| CS-01 |
24/7 |
11/15/2012 |
RRFB |
3/6/2014 |
4/2/2014 |
11/27/2014 |
2/14/2014 |
| CS-02 |
None |
1/28/2013 |
CRFB |
11/27/2014 |
2/5/2014 |
3/6/2014 |
4/1/2014 |
| FG-01 |
Activated |
5/21/2013 |
RRFB |
1/9/2014 |
3/5/2014 |
9/2/2013 |
10/23/2013 |
| FG-02 |
RRFB |
NAb |
RRFB |
1/9/2014 |
3/5/2014 |
7/11/2013 |
10/22/2013 |
| FG-03 |
None |
5/21/2013 5/22/2013 |
CRFB |
9/7/2013 |
10/23/2013 |
12/4/2013 |
3/5/2014 3/6/2014 |
| MK-04 |
None |
6/18/2013 |
CRFB |
8/1/2013 |
9/24/2013 |
10/21/2013 |
12/5/2013 |
| MK-05 |
None |
6/19/2013 |
CRFB |
8/1/2013 |
9/23/2013 |
10/21/2013 |
12/5/2013 |
| MK-06 |
None |
NAc |
CRFB |
8/5/2013 |
9/23/2013 |
10/21/2013 |
12/5/2013 |
| MK-07 |
RRFB |
NAb |
RRFB |
10/21/2013 |
12/6/2013 |
Existing condition |
6/19/2013 |
| MK-08 |
RRFB |
NAb |
RRFB |
10/21/2013 |
12/4/2013 |
Existing condition |
6/20/2013 |
a24/7 = continuously active yellow flashing beacons; Activated = pedestrian-activated yellow flashing beacons.
bNo before data collected because the RRFBs were already installed at the site.
cRoad work was being conducted near the site during the data collection trip; therefore, no before data were collected.
NA = Not Available.
The study was conducted between November 2012 and April 2014. The before data were collected between November 2012 and August 2013. Once the before data were obtained, the research team requested the city to install the initial device—at approximately half the sites, the initial device was the RRFB; at the other half of the sites, it was the CRFB. Following installation of the initial device (and a minimum period of 1 month for drivers to get acclimated to the new device), the research team collected “after data.” Once the after data were obtained, the research team requested the city to install the second device (thus, RRFBs were replaced with CRFBs and vice versa). Once again, following a minimum period of 1 month for drivers to get acclimated to the second device, the research team collected after data for the second device. The CRFB and RRFB data were collected between June 2013 and April 2014.
Data were collected primarily during the daytime when vehicles were free-flowing. Because few, if any, studies have collected data at night, the research team wanted to obtain some data for nighttime conditions. The characteristics of the beacon and the site might have different impacts on driver yielding during night conditions compared with daytime conditions. Therefore, nighttime data were collected for one of the sites in each city.
The research team used a staged pedestrian protocol to collect driver yielding data to ensure that oncoming drivers receive a consistent presentation of approaching pedestrians. Under this protocol, a member of the research team acted as a pedestrian using the crosswalk, to stage the conditions under which driver yielding would be observed. Each staged pedestrian wore similar clothing (gray t-shirt, blue jeans, and gray tennis shoes) and followed specific instructions in crossing the roadway. The staged pedestrian was accompanied by a second researcher, who observed and recorded the yielding data on pre-printed datasheets. Additional information on the staged pedestrian protocol followed is available in a recent paper.(12) For this study, data for a minimum of 60 staged pedestrian crossings were collected at each site in each time period during daytime. Because of the length of time needed to collect the crossing data, data for a minimum of 40 staged pedestrians were collected at night with one exception. Because of the very low yielding and the frequency of the staged pedestrian being stranded in the TWLTL, data collection was stopped at one of the sites.
The team also video-recorded the sites for approximately 4 to 6 hours for each study period. The video data provided the opportunity to confirm characteristics of a crossing, including whether the pedestrian pushed the pushbutton to activate the beacons. Volume counts were reduced for a sample of the video recorded at the RRFB sites.
Formal definitions of luminance intensity, brightness, optical power, and other photometric measurement terms are listed in table 163. While the term optical power is more traditionally associated with optical convergence or divergence of a lens, in this memo, the SAE definition is used.(35)
The equipment responsible for the light measurements includes a photometer with a cosine-corrected photometric sensor and an oscilloscope with high-speed photodetector. The cosine-corrected photometric sensor is rated to capture light with wavelengths between 400 and 700nanometers, which is also the spectrum of visual light. The high-speed photodetector is rated for capturing light with wavelengths between 400 and 1,100 nanometers, which includes infrared light in addition to the visual spectrum of light.(36) All of the equipment used and purpose of the equipment are listed in table 164.
Table 163. Photometric terminology.
Term |
Definition |
| Brightness | “Attribute of a visual perception according to which an area appears to emit, or reflect, more or less light.”(37) |
| Illuminate energy (lux-seconds) |
Quantity of light falling on a sensor from a light source. |
| Luminous Intensity (candela) | “The luminous flux per unit solid angle in a given direction expressed in candela (cd).”(38) (p. 1) |
| Luminous energy (candela-seconds) |
Luminous flux per unit solid angle in a given direction for a duration of time. |
| Optical Power (candela-seconds/minute) |
“The integration of the luminous intensity of the flashing light source for a time of 60 seconds.”(35) (p. 3) |
| Light Pulse | “A single, visually continuous emission of optical energy. High frequency modulation is permitted.”(35) (p. 3) |
| Flash | “A flash is a light pulse or a train of light pulses, where a dark interval of at least 160 ms separates the light pulse or the last pulse of the train of light pulses from the next pulse or the first pulse of the next train of light pulses.”(35) (p. 3) |
Table 164. Equipment list and purpose.
Equipment |
Purpose |
| Photometer with cosine-corrected photometric sensor(39) | Illuminating energy measurement (lux-seconds) |
| Oscilloscope with high-speed photodetector | Capturing flash pattern (time) Determining relative beacon intensity |
| Tripod and mounting equipment | Positioning the photometric sensor and photodetector in front of the beacons |
| Laptop computer | Recording the illuminate energy and capturing the flash pattern |
| Portable generator | Powering the photometer and oscilloscope |
| Electric measuring tape | Measuring the distance between the cosine-corrected photometric sensor and the light source |
Researchers collected illuminate energy and flash pattern digital images of beacons in cities participating in the CRFB/RRFB open-road study. The dates of the data collection by site are listed in table 165. All of the data were collected at night because ambient light from the sun would overwhelm the sensors if researchers used the same methods during the day.
Table 165. Data collection dates by site and city.
Site ID |
Beacon shape |
City |
Night(s) |
| AU-01 | Circular |
Austin |
March 6 to 7, 2014 |
| AU-02 | Rectangular |
Austin |
March 6 to 7, 2014 |
| CS-01 | Rectangular |
College Station |
January 21, 2014 |
| CS-02 | Circular |
College Station |
January 21, 2014 |
| FL-01 | Circular |
Flagstaff |
March 3 to 5, 2014 |
| FL-02 | Circular |
Flagstaff |
March 3 to 5, 2014 |
| FL-03 | Rectangular |
Flagstaff |
March 3 to 5, 2014 |
| MI-04 | Circular |
Milwaukee |
September 22 to 24, 2013 |
| MI-05 | Circular |
Milwaukee |
September 22 to 24, 2013 |
| MI-06 | Circular |
Milwaukee |
September 22 to 24, 2013 |
| MI-07 | Rectangular |
Milwaukee |
September 22 to 24, 2013 |
| MI-08 | Rectangular |
Milwaukee |
September 22 to 24, 2013 |
Upon arriving at the data collection location, researchers would mount the photometric sensor and high-speed photodetector to the tripod. Then, to the best of their ability, the researchers positioned the cosine-corrected photometric sensor in front of the yellow warning beacons such that measurements were taken at a horizontal (left/right) angle of zero degrees and a vertical (up/down) angle of zero degrees. In addition, researchers positioned the photometric sensor between 3 and 12 ft away from the beacons. In this study, the beacons were either 12‑inch circular beacons mounted below the sign or rectangular beacons mounted below the sign.
After positioning the sensors, the research team confirmed the equipment was working properly before taking measurements. The researcher responsible for taking measurements took five measurements of background illuminate energy. During data reduction, researchers used these measurements to quantify and remove background illuminate energy from the calculated values of luminance energy and luminance intensity for the beacons. Background illuminate energy often came from streetlights. The duration of the illuminate energy readings was between 1 and 2s depending on the distance from the light source and volume of illuminate energy. (The photometer was unable to record illuminate energy values greater than 500 lx-s.)
After taking the background illuminate energy readings, the research team activated the beacons and took digital images of the flash pattern using the high-speed photodetector and digital oscilloscope. Each digital image consisted of 4 s worth of data recorded as 4,000 individual energy readings. (The high-speed photodetector and oscilloscope documented the flash pattern in terms of voltage.) Each digital image was saved to the computer in a spreadsheet.
Once the digital images of the flash patterns were recorded, the researcher responsible for taking measurements took five illuminate energy readings while the beacons were activated (flashing). The duration for each reading was the same as the duration of the background readings.
Before moving the sensors to the next set of beacons at the site, the research team recorded the distance from the cosine-corrected photometric sensor to the light source in meters. During data reduction, researcher used this value to convert illuminate energy (lx-s) to luminance energy
(cd-s). In addition, the research team documented which beacon (left or right) in the set had two pulses and which beacon had more than two pulses.
After confirming all of the necessary data were collected, the research team then moved to the next set of beacons at the site. It took the research team between 90 and 180 min to collect all of the illuminate energy readings and flash pattern images required for sites with four sets of beacons to measure.
After completing the data collection, researchers entered the crossing data and the site characteristics data from the field worksheets into an electronic database. The average yielding rate for a site was calculated as shown in figure 88; however, data for individual crossings were used in the statistical evaluation.
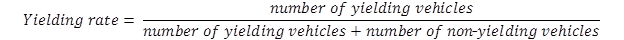
Figure 88. Equation. Yielding rate for a single crossing and average yielding rate for a site.
Determine Luminance Energy and Optical Power for Each Set of Beacons
The first step in determining the luminance intensity and luminance energy for each set of beacons and individual lamps was to average the illuminate energy background measurements and illuminate energy readings when the beacons were active. Researchers then subtracted the average background illuminate energy from the average illuminate energy with activated beacons to determine the average beacon illuminate energy. Average beacon illuminate energy is then converted to luminance energy using the equation in figure 89.
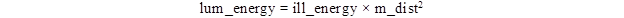
Figure 89. Equation. Average luminance energy.
Where:
lum_energy = average beacon luminance energy (cd-s).
ill_energy = average beacon illuminate energy (lx-s).
m_dist = distance between the cosine-corrected photometric sensor and the beacons (m).
After determining the average luminance energy, researchers converted luminance energy to optical power, which is luminance energy per minute. For this memo, optical power is calculated using the equation in figure 90:
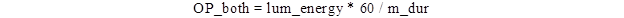
Figure 90. Equation. Optical power.
Where:
lum_energy = average beacon luminance energy (cd-s).
m_dur = duration of the illuminate energy reading used to calculate luminance energy (s).
OP_both = optical power of the beacon set (cd-s/min).
Determine on Time and Cycle Length for Each Beacon Set
After determining the optical power for each set of beacons, the next step in the process of determining the luminous intensity for individual beacons is to determine the total on time, individual lamp on time, and cycle length for each beacon. To determine these values, researchers used the digital images of the flash patterns captured using the oscilloscope and high-speed photodetector.
The first step in the process of determining on time and cycle length is to convert the voltage values in the digital images to percent maximum voltage; then, to determine which values count as on and which values count as off, researchers used a trigger level of 10 percent of the maximum voltage. This means that if the percent maximum voltage was under 10 percent, then the lamp was considered to be off and that time was assigned a percent maximum voltage of zero. Sometimes, owing to background illuminate energy, researchers adjusted up to 20 percent of the maximum voltage, but this rarely occurred.
Next, researchers used a computer macro to sort the data into four separate flash cycles of about 800 ms. A researcher then graphed each flash cycle and reviewed these graphs to make sure the image was captured correctly before performing calculations. An example of a graphed flash cycle that was captured correctly is shown in figure 91.
Each data point in figure 91 represents 1 ms of data. Therefore, to determine cycle length, researchers counted the number of data points in each correctly captured flash cycle and averaged these values to determine the cycle length in milliseconds. To determine on time, researchers counted the number of data points that were greater than zero and averaged these values to determine the on time in milliseconds. Owing to background lighting, some points that were greater than zero would be filtered to zero during the data analysis. This ensured that readings that were greater than zero based on the background light and not the beacon being active were accounted for properly.
After determining the total on time and cycle length, researchers then determined the on time for the beacon with five flashes (the first five flashes in figure 91) and the on time for the beacon with two flashes (the sixth and seventh flashes in figure 91).
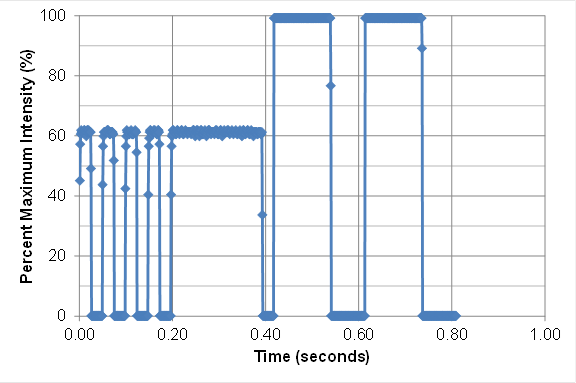
Figure 91. Graph. Example of correctly captured and graphed flash cycle showing five pulses of light (0.0 to 0.4 time) followed by two pulses of light (0.4 to 0.8 time).
Table 166 shows the driver yielding results for each site and assembly along with the number of nonstaged and staged pedestrian crossings for the daytime data collection periods. During the daytime, driver yielding to staged pedestrians averaged 63 percent for the CRFB and 59 percent for the RRFB assemblies. The range of driver yielding to staged pedestrians at yellow, rapid-flashing beacons ranged from a low of 22 percent to a high of 98 percent.
Table 167 lists the driver yielding rates for the nighttime data collection periods. Driver yielding to staged pedestrians at night averaged 72 percent for the RRFB assemblies and 49 percent for the CRFB assemblies; however, the 49 percent figure includes data for a site that had a beacon that did not meet the Class 1 requirement for brightness. Without that site, the average yielding for the CRFB was 69 percent.
Table 166 and table 167 also contain the driver yielding rates in the before condition (i.e., before the installation of the rapid-flashing beacon) for those sites where data were available. An evaluation of whether a statistically significant increase was present between the before conditions (slow flashing beacon or no flashing treatment) and the rapid-flashing beacon condition could not be completed because of the limited number of sites with a before treatment.
Table 166. Daytime driver yielding rate by site and assembly.
Assembly |
Site |
Nonstaged count |
Nonstaged driver yielding |
Staged count |
Staged driver yielding |
CRFB |
AU-01 |
28 |
90% |
60 |
62% |
AU-02 |
13 |
54% |
60 |
57% |
|
CS-01 |
41 |
97% |
39 |
89% |
|
CS-02 |
11 |
48% |
60 |
36% |
|
FG-01 |
131 |
83% |
81 |
94% |
|
FG-02 |
73 |
93% |
69 |
95% |
|
FG-03 |
37 |
90% |
66 |
95% |
|
MK-04 |
109 |
12% |
62 |
58% |
|
MK-05 |
104 |
13% |
78 |
44% |
|
MK-06 |
130 |
22% |
56 |
67% |
|
MK-07 |
62 |
58% |
62 |
39% |
|
MK-08 |
30 |
30% |
60 |
58% |
|
All CRFB |
769 |
46% |
753 |
63% |
|
All CRFB (without site CS-02) |
717 |
44% |
654 |
67% |
|
RRFB |
AU-01 |
26 |
71% |
60 |
71% |
AU-02 |
82 |
43% |
60 |
59% |
|
CS-01 |
58 |
97% |
60 |
56% |
|
CS-02 |
17 |
49% |
60 |
44% |
|
FG-01 |
95 |
77% |
69 |
84% |
|
FG-02 |
77 |
92% |
61 |
98% |
|
FG-03 |
25 |
98% |
80 |
98% |
|
MK-04 |
79 |
25% |
61 |
43% |
|
MK-05 |
40 |
24% |
59 |
22% |
|
MK-06 |
36 |
23% |
61 |
57% |
|
MK-07 |
114 |
48% |
61 |
31% |
|
MK-08 |
128 |
37% |
82 |
36% |
|
All RRFB |
777 |
57% |
774 |
59% |
|
Slow |
AU-01 |
83 |
22 |
60 |
12 |
AU-02 |
33 |
26 |
61 |
51 |
|
CS-01 |
77 |
100 |
42 |
66 |
|
FG-01 |
89 |
79 |
100 |
85 |
|
All Slow Flashing |
282 |
58 |
263 |
54 |
|
None |
CS-02 |
10 |
10 |
40 |
9 |
FG-03 |
37 |
87 |
80 |
62 |
|
MK-04 |
121 |
18 |
96 |
19 |
|
MK-05 |
88 |
12 |
89 |
9 |
|
All No Flashing |
256 |
26 |
305 |
24 |
|
Table 167. Nighttime driver yielding rate by site and assembly.
Assembly |
Site |
Nonstaged count |
Nonstaged driver yielding |
Staged count |
Staged driver yielding |
| CRFB | AU-02 | 0 | NA | 40 | 67% |
| CS-02 | 0 | NA | 19a | 5%a | |
| FG-01 | 23 | 85% | 52 | 89% | |
| MK-08 | 6 | 56% | 60 | 52% | |
| All CRFB (without site CS-02) | 29 | 78% | 152 | 69% | |
| RRFB | AU-02 | 0 | NA | 40 | 88% |
| CS-02 | 0 | NA | 40 | 53% | |
| FG-01 | 21 | 100% | 50 | 95% | |
| MK-08 | 9 | 20% | 50 | 54% | |
| All RRFB | 30 | 84% | 180 | 72% | |
| Slow | FG-01 | 7 | 100% | 58 | 63% |
aData should not be considered because beacon brightness did not satisfy the Class 1 requirement.
NA = Not Applicable (no nonstaged pedestrians were observed at night at these sites).
After determining the cycle length, total on time, on time for the five-flash beacon, and on time for the two-flash beacon, it is possible to determine the average luminance intensity for each beacon set and individual beacons. The equation for determining the average intensity for each beacon set is shown in figure 92:
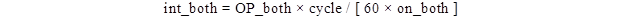
Figure 92. Equation. Average intensity.
Where:
int_both = the average luminance intensity for both beacons (cd).
cycle = cycle length for the beacon set (ms).
on_both = total on time for both beacons (ms).
OP_both = optical power of the beacon set (cd-s/min).
Determine Optical Power and Average Luminance Intensity by Approach
The optical power by approach can be calculated using the equation in figure 93.
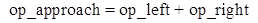
Figure 93. Equation. Optical power by approach.
Where:
op_approach = optical power for a vehicle traveling in a given direction (cd-s/min).
op_left = optical power for a set of beacons on the left side of the roadway (cd-s/min).
op_right = optical power for a set of beacon on the right side of the roadway (cd-s/min).
The average intensity by approach can be calculated using the equation in figure 94.
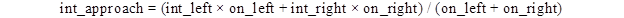
Figure 94. Equation. Average intensity by approach.
Where:
int_approach = average intensity for an approach (cd)
int_left = intensity for a set of beacons on the left side of the roadway (cd).
on_left = on time for the set of beacons on the left side of the roadway (s).
int_right = intensity for a set of beacons on the right side of the roadway (cd).
on_right = on time for the set of beacons on the right side of the roadway (s).
Determine Optical Power and Average Luminance Intensity by Site
Because motorist yielding calculations are done for a site rather by an approach, a value is needed to reflect the site. The average optical power for a site would be the average of the two directions or approaches. The optical power for an approach is the sum of the optical power for the assembly on the left and the assembly on the right because a driver would have both assemblies in view. For a site, the driver would only have the assemblies on approach A or on approach B in view; therefore, an average the optical power for the two approaches is needed. It can be calculated using the equation in figure 95.
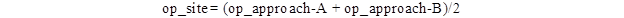
Figure 95. Equation. Optical power for a site.
Where:
op_site = average optical power for site (cd-s/min).
op_approach-A = optical power for a vehicle traveling in a given direction (cd-s/min).
op_approach-B = optical power for a vehicle traveling in the opposing direction (cd-s/min).
To provide an appreciation of how long a beacon is on, the average intensity for a site should be a weighted average. It can be calculated using the equation in figure 96:
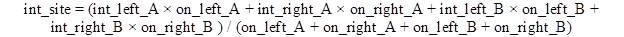
Figure 96. Equation. Average intensity for a site.
Where:
int_site = average intensity for a site (cd).
int_left_A = intensity for left-side beacons on approach A (cd).
int_right_A = intensity for right-side beacons on approach A (cd).
int_left_B = intensity for left-side beacons on approach B (cd).
int_right_B = intensity for right-side beacons on approach B (cd).
on_left_A = on time for left-side beacons on approach A (s).
on_right_A = on time for right-side beacons on approach A (s).
on_left_B = on time for left-side beacons on approach B (s).
on_right_B = on time for right-side beacons on approach B (s).
The measured average optical power and average intensity by site are provided in table 168 and table 169, respectively. Figure 97 shows a plot of the optical power values while figure 98 shows average intensity per site. In most cases, the research team was able to track where the beacons were moved after a rotation.
Table 168. Average optical power and intensity by crossing.
| Shape | Site |
Average intensity (cd), rounded to hundreds |
Average optical power (cd-s/min), rounded to thousands |
| CRFB | AU-01 |
500 |
37,000 |
| RRFB | AU-02 |
3,000 |
226,000 |
| RRFB | CS-01 |
1,400 |
117,000 |
| CRFB | CS-02 |
100 |
8,000 |
| CRFB | FG-01 |
1,800 |
156,000 |
| CRFB | FG-02 |
1,100 |
80,000 |
| RRFB | FG-03 |
1,200 |
93,000 |
| CRFB | MK-04 |
1,100 |
87,000 |
| CRFB | MK-05 |
2,100 |
162,000 |
| CRFB | MK-06 |
1,900 |
150,000 |
| RRFB | MK-07 |
1,100 |
84,000 |
| RRFB | MK-08 |
800 |
66,000 |
Table 169. Device brightness at each site.
Site |
CRFB-intensity (cd) |
CRFB-optical power (cd-s/min) |
RRFB-intensity (cd) |
RRFB-optical power (cd-s/min) |
| AU-01 | 600 | 37,000 | 3,100 | 220,000 |
| AU-02 | 600 | 37,000 | 3,100 | 220,000 |
| CS-01 | 100 | 8,000 | 1,500 | 117,000 |
| CS-02 | 100 | 8,000 | 1,500 | 117,000 |
| FG-01 | 1,900 | 165,000 | NA | NA |
| FG-02 | 1,200 | 83,000 | NA | NA |
| FG-03 | NA | NA | 1,200 | 95,000 |
| MK-04 | 1,100 | 87,000 | 1,200 | 91,000 |
| MK-05 | 2,100 | 162,000 | 1,000 | 77,000 |
| MK-06 | 1,900 | 150,000 | 800 | 66,000 |
| MK-07 | 1,600 | 124,000 | 1,100 | 84,000 |
| MK-08 | 1,900 | 150,000 | 800 | 66,000 |
NA = Not Available.
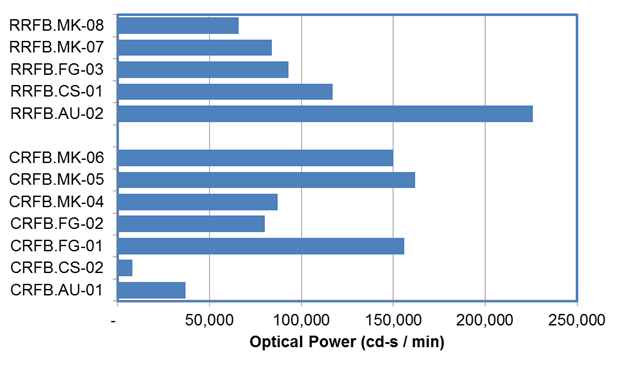
Figure 97. Graph. Plot of average optical power by beacon shape and site.
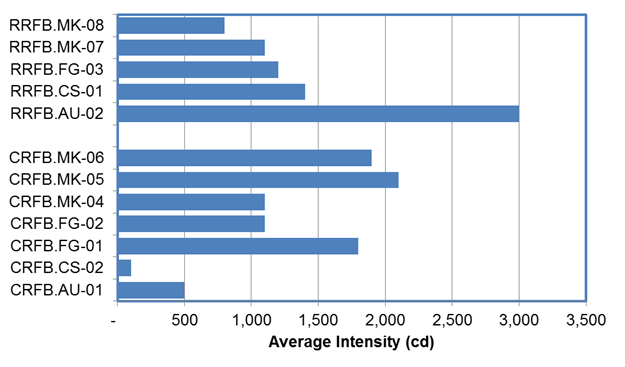
Figure 98. Graph. Plot of average intensity by beacon shape and site.
When a driver approaches a pedestrian crossing, the driver either yields and stops (or slows) the vehicle or does not yield to the waiting pedestrian. This binary behavior (yield or no yield) can be modeled using logistic regression. A significant advantage of using logistic regression is it permits consideration of individual crossing data rather than reducing all the data at a site to only one value. For the dataset available in this study, that means more than 2,500 data points could be available (i.e., all the unique staged crossings recorded) rather than only 41 data points (i.e., the number of study sites by number of assemblies and by day or night). For the analyses that focused on comparing the CRFB to the RRFB, that means 1,878 data points rather than 32data points are available. When examining both staged and nonstaged data, there are 3,483crossings available. These larger sample sizes could result in finding significant relationships that would not be apparent with a smaller dataset. In addition, it is possible to use random effects to account for site-specific differences because such differences induce a correlation structure in the dataset.
Using logistic regression to model the relationships assumes that the logit transformation of the outcome variable (i.e., yielding rate) has a linear relationship with the predictor variables, which results in challenges in interpreting the regression coefficients. The interpretation of such coefficients is not based on the yield rate changes directly, but a change in the odds of motorists yielding. (The odds are defined as the ratio of the number of yielding motorists to the number of non-yielding motorists.) The regression coefficients can be transformed and interpreted as odds ratios of different levels of the corresponding independent variable. In other words, a unit change of the independent variable corresponds to a change in the odds of motorists yielding, which is an alternative way to express a change in yielding rate. More details on these types of models can be found in the statistical literature.(40) All the statistical analyses were performed using R, an open-source statistical language and environment and two open-source packages for fitting GLMMs.(41,42,27)
Because a previous study that included RRFBs found that posted speed limit, crossing distance, and city influenced driver yielding, the initial analyses were also conducted with those variables.(12) In addition, a measure of the rotation was also recorded, to potentially account for a learning curve in the driver yielding rates, as was indicated in the TxDOT study.(12) Therefore, the variable “order” was added as a nested random effect in each site.
Preliminary modeling revealed a correlation between crossing distance and speed limit present in the dataset; therefore, only crossing distance was included in the final model. Attempts were made to conduct the analysis separately for nighttime and daytime conditions; however, insufficient data were available for the nighttime analysis. To determine whether nighttime results were significantly different from daytime results, an indicator variable for nighttime conditions was included in the final model. The model specification was a quasi-binomial regression because the dataset exhibited significantly more dispersion than it would be expected for binomially distributed data. This type of model adjusts maximum likelihood standard errors using an estimate of overdispersion to reduce risk of type-I error in the analysis.
From the preliminary review of the results in table 166, it appears that there are only minor, if any, differences between the CRFB and the RRFB. The results from the GLMM are shown in table 170, and these results support that observation. These results indicate that there are no significant differences between the two beacon shapes (p-value = 0.4792). The day/night variable was not significant (p-value = 0.5152), which indicates that there is not enough nighttime data to differentiate from daytime rates as a flat effect, after accounting for the rest of the variables in the analysis. Preliminarily, it appears that the city of Flagstaff has notably higher driver yielding compared with the base city of Austin (an adjusted p-value for multiple comparisons is required to make a formal assessment) while College Station and Milwaukee are clearly not different from Austin. The model also showed that calculated daily traffic was not a significant variable (p-value = 0.3157). The results also revealed that the correlation in the data structure and order of installation are rather weak effects, judging by the intraclass correlation coefficient, which is a measure of how similar data points are within groups when aggregated by site and by order of installation.
Table 170. GLMM results comparing CRFB to RRFB.
Variablea,b |
Estimate |
Standard error |
DF |
t-value |
p-value |
| Reference Levelc | 1.94372 |
0.706795 |
1,837 |
2.750049 |
0.006 |
| City: College Station | -0.24829 |
0.700020 |
6 |
-0.354687 |
0.735d |
| City: Flagstaff | 2.37791 |
0.512182 |
6 |
4.642705 |
0.0035d |
| City: Milwaukee | -0.80018 |
0.439072 |
6 |
-1.822435 |
0.1182d |
| CrossDis | -0.02137 |
0.021964 |
6 |
-0.973127 |
0.3681 |
| Treatment: RRFB | -0.15289 |
0.205130 |
11 |
-0.745352 |
0.4717 |
| Day.Night: Night | 0.07484 |
0.113837 |
1,837 |
0.657453 |
0.511 |
| Calculated Daily Traffic | -0.00004 |
0.000037 |
6 |
-1.094477 |
0.3157 |
aColumn headings are defined as follows:
- Variable: Fixed Effects variables included in model.
- Estimate: natural logarithm of the ratio: Odds(coefficient level)/Odds(reference level). In the case of reference level, Estimate is the log-odds of the average yielding rate at the reference level.
- Standard Error = Standard error of value.
- DF = degrees of freedom.
- t-value = conservative estimate of the z-value, which is the standard normal score for estimate, given the hypothesis that the actual odds ratio equals one.
- p-value: Probability that the observed log-odds ratio be at least as extreme as estimate, given the hypothesis that the actual odds ratio equals one.
bRandom effects variables: Site (intraclass correlation coefficient = +0.045) and Site X Order (intraclass correlation coefficient = +0.169).
cReference Level Yielding in the model is estimated at 78.02 percent for the following conditions:
- City = Austin.
- Day.Night = Day.
- Treatment = CRFB.
dThese p-values require an adjustment for multiple comparisons if inferences about different yielding rates among cities are intended.
Comparison of CRFB to RRFB Considering Beacon Brightness
For a subset of the sites, the brightness of the beacons was measured. The results for the analysis that included intensity as a measure of brightness are shown in table 171. Again, the findings illustrate, preliminarily, that driver yielding in Flagstaff is higher than in Austin. This analysis included a separate account of intensity under those conditions because the effects of beacons might differ between daytime and nighttime.
Figure 99 for daytime and figure 100 for nighttime show graphs of average driver yielding per site versus intensity that illustrate a trend of increasing driver yielding associated with increases in intensity. Furthermore, the statistical analysis results also demonstrated an increasing yielding rate with increasing intensity; however, only at night (p-value < 0.0001 from the quasi-binomial regression model, see Intensity:Night in table 171). Still, the trend is in the same direction during the day but with a smaller magnitude that the analysis found statistically insignificant. It is estimated that the odds of yielding at night increase by a multiplicative factor of 1.0008 per additional candela of intensity.
Including brightness in the analysis does not modify the findings for treatment. Without brightness, the results (as shown in table 170) are that there was no difference between the circular and rectangular shaped beacons. When considering brightness, the circular beacons still do not have significantly different yielding rates compared with rectangular beacons (as shown in table 171). Table 172 and table 173 show the estimated daytime and nighttime effects on a theoretical site for the range of intensity in this study (100 to 3,100 cd). For reference, column 5 of these tables shows the raw data averages. The sixth column shows how many crossings are available to compute the raw data estimates. The results demonstrate the strong effect for intensity at night that is also evident in the raw data averages.
Table 171. GLMM results comparing CRFB to RRFB when beacon brightness data are available.
Variablea,b |
Estimate |
Standard error |
DF |
t-value |
p-value |
| Reference Levelc | 1.2670 |
0.7413 |
1,593 |
1.7091 |
0.0876 |
| City: College Station | 0.2310 |
0.6303 |
7 |
0.3669 |
0.7245d |
| City: Flagstaff | 2.2340 |
0.4830 |
7 |
4.6261 |
0.0024d |
| City: Milwaukee | -0.5060 |
0.4006 |
7 |
-1.2620 |
0.2474d |
| CrossDis | -0.0260 |
0.0197 |
7 |
-1.3330 |
0.2243 |
| Treatment: RRFB | -0.2430 |
0.1567 |
7 |
-1.5528 |
0.1644 |
| Intensity | 0.0002 |
0.0001 |
7 |
1.5855 |
0.1569 |
| Day.Night: Night | -0.8910 |
0.2320 |
1,593 |
-3.8412 |
0.0001 |
| Intensity X Day.Night | 0.0007 |
0.0002 |
1,593 |
4.4355 |
< 0.0001 |
aColumn headings are defined as follows:
- Variable: Fixed Effects variables included in model.
- Estimate: natural logarithm of the ratio: Odds(coefficient level)/Odds(reference level). In the case of reference level, Estimate is the log-odds of the average yielding rate at the reference level.
- Standard Error = Standard error of value.
- DF = degrees of freedom.
- t-value = conservative estimate of the z-value, which is the standard normal score for estimate, given the hypothesis that the actual odds ratio equals one.
- p-value: Probability that the observed log-odds ratio be at least as extreme as estimate, given the hypothesis that the actual odds ratio equals one.
bRandom effects variables: Site (intraclass correlation coefficient = +0.093) and Site X Order (intraclass correlation coefficient = +0.138).
cReference Level Yielding in the model is estimated at 78.02 percent for the following conditions:
- City = Austin.
- Day.Night = Day.
- Treatment = CRFB.
dThese p-values require an adjustment for multiple comparisons if inferences about different yielding rates among cities are intended.
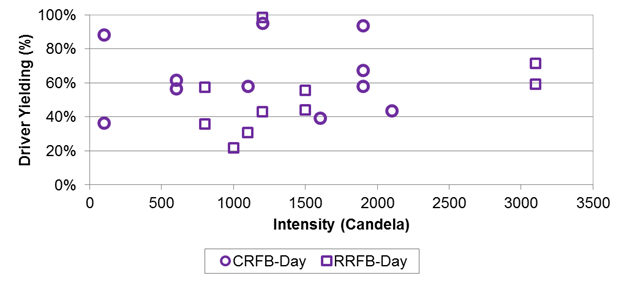
Figure 99. Graph. Driver yielding compared with beacon brightness intensity for day.
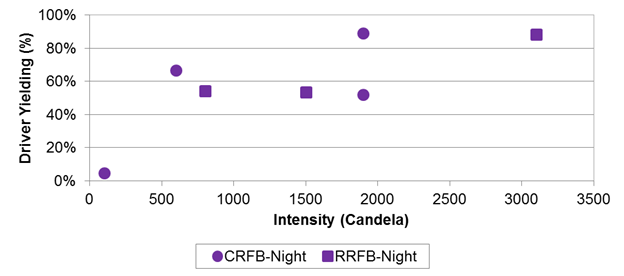
Figure 100. Graph. Driver yielding compared with beacon brightness intensity for night.
Table 172. Daytime effect of intensity on driver yielding for a theoretical site and for the raw data averages.
| Intensity (cd) | Odds ratio |
Initial YR = 50 percent (percent) |
Initial YR = 60 percent (percent) |
Initial YR = 70 percent (percent) |
Raw data average (percent) |
Number of crossings |
| 100 |
1.02 |
50.0 |
60.0 |
70.0 |
58.8 |
91 |
| 800 |
1.14 |
53.4 |
63.2 |
72.8 |
54.8 |
143 |
| 1,900 |
1.38 |
58.0 |
67.4 |
76.3 |
78.6 |
197 |
| 3,100 |
1.69 |
62.8 |
71.7 |
79.8 |
71.2 |
120 |
YR = Yielding Rate.
Table 173. Nighttime effect of intensity on driver yielding for a theoretical site and for the raw data averages.
| Intensity (cd) | Odds Ratio |
Initial YR = 50 percent (percent) |
Initial YR = 60 percent (percent) |
Initial YR = 70 percent (percent) |
Raw data average |
Number of crossings |
| 100 |
1.09 |
50.0 |
60.0 |
70.0 |
6.3 |
19 |
| 800 |
1.97 |
66.3 |
74.7 |
82.1 |
66.7 |
50 |
| 1,900 |
4.98 |
83.3 |
88.2 |
92.1 |
78.3 |
112 |
| 3,100 |
13.73 |
93.2 |
95.4 |
97.0 |
92.9 |
40 |
YR = Yielding Rate.
When considered together, analysis of results from table 172 and table 173 indicate that the difference in yielding rate associated with the day or night varies depending on the beacon intensity level, as shown in table 174. This table shows that nighttime driver yielding was significantly lower than daytime when the intensity was 800cd or less. If a 0.10 significance level is used, daytime yielding is significantly higher than nighttime for intensities larger than 1,800 cd.
Table 174. Multiple comparisons for natural light effect on driver yielding by intensity.
| Odds ratio (OR) compared to 1.0 | OR | Ln(OR) | Standard error | z-value | p-value | Significanta |
| Night/Day (0 cd) | 0.41 | -0.89142 | 0.23142 | -3.852 | <0.001 | *** |
| Night/Day ( 800 cd) | 0.70 | -0.35079 | 0.14502 | -2.419 | 0.0401 | * |
| Night/Day (1,400 cd) | 1.06 | 0.05468 | 0.12660 | 0.432 | 0.8983 | — |
| Night/Day (1,800 cd) | 1.38 | 0.32499 | 0.14807 | 2.195 | 0.0698 | — |
aSignificance values are as follows: — = p-value > 0.05, * = p-value ≤ 0.05, ** = p-value < 0.01 *** = p-value < 0.001.
Comparison of Driver Yielding When Beacon Activated to Beacon Not Activated
The purpose of a rapid-flashing beacon—whether it is circular or rectangular—is to draw drivers’ attention to a pedestrian waiting to cross the roadway and, thus, encourage drivers to yield to that pedestrian. Therefore, a key question to be answered in the research was to what extent did the presence of an actively flashing beacon influence driver yielding. To address this question, driver yielding rates were compared between the pedestrian crossings when a beacon was activated and the pedestrian crossings when a beacon was not activated.
The analysis included RRFBs and CRFBs and focused on crossings during daytime study periods. An initial comparison of staged pedestrian crossings (Note: staged pedestrians activated the beacon every time they crossed the roadway) and those nonstaged pedestrian crossings for which the beacon was activated showed no statistically significant difference in driver yielding. Therefore, the analysis included both staged and nonstaged pedestrian crossings.
The data consisted of a total of 1,970 activated and 476 non-activated crossings, for a total of 2,446 crossings used in the analysis. The distribution of activated and non-activated crossings in each city and site is shown in table 175.
Table 175. Number of activated and non-activated crossings by city and site.
| Site | Beacon activation | Total | ||
Yes |
No | |||
| Austin |
AU-01 |
149 |
9 |
158 |
AU-02 |
134 |
44 |
178 | |
| College Station |
CS-01 |
126 |
5 |
131 |
CS-02 |
136 |
4 |
140 | |
| Flagstaff |
FG-01 |
266 |
71 |
337 |
FG-02 |
255 |
16 |
271 | |
FG-03 |
192 |
4 |
196 | |
| Milwaukee |
MK-04 |
130 |
95 |
225 |
MK-05 |
147 |
39 |
186 | |
MK-06 |
132 |
98 |
230 | |
MK-07 |
147 |
46 |
193 | |
MK-08 |
156 |
45 |
201 | |
| Total |
1,970 |
476 |
2,446 | |
A GLMM with a binomial distribution and logit link was used to model the probability of yielding as a function of the following variables:
- Beacon activation (Yes/No).
- City (4 levels).
- Interaction between beacon activation and city (8 levels).
- CDT (continuous; ranging from approximately 2,130 to 23,008 vehicles/day).
- Crossing distance (continuous; ranging from 21 to 60 ft).
The data collection site within each city was included in the model as a random effect to account for differences among sites. Model estimation was done using PROC GLIMMIX in SAS. Stepwise backward-elimination was used to identify which factors and interaction were statistically significant at the 5-percent level. At each step, the factor, or interaction, with the highest p-value above 0.05 from a type 3 analysis F-test was excluded and the model rerun. A Type 3 analysis F-test determines the significance of each variable in the model individually. The results of this approach to obtain the final model, including beacon activation, city, and CDT as significant variables at the 0.05 level, are summarized in table 176.
Table 176. Stepwise elimination procedure results.
| Step in | Type 3 p-value for each factor in the ANOVA model | ||||
Beacon activation |
City |
Beacon activation times city interaction |
CDT (vehicles/day) |
Crossing distance | |
| Step 1 | < .0001 |
< .0001 |
0.40 |
0.15 |
0.94 |
| Step 2 | < .0001 |
< .0001 |
0.40 |
0.08 |
— |
| Step 3 | < .0001 |
< .0001 |
— |
0.07 |
— |
| Final | < .0001 |
< .0001 |
— |
— |
— |
p-values above 0.05 are not significant.
— Not Applicable.
Those variables significant at the 0.05 level—beacon activation and city—were included in the GLMM evaluation. The ANOVA results of the reduced model, containing beacon activation and city as statistically significant factors, are shown in table 177. The logistic regression results, on a logit scale, as well as the results of the type 3 analysis, are shown. The probability associated with the t-value (columns 6 and 7) indicates whether the corresponding coefficient is statistically significantly different from zero. The reference level (baseline) for this analysis was defined as non-activated beacons (of either type) in Milwaukee, WI.
Table 177. GLMM results comparing driver yielding rates between activated and non‑activated beacons.
Effect |
Level |
Coefficient estimate |
Standard error |
DF |
t-value |
Pr > |t| |
Type 3 analysis F-value |
Type 3 analysis Pr > F |
| Intercept | Intercept |
-1.51 |
0.26 |
8 |
-5.72 |
0.0004 |
— |
— |
| Beacon activation |
Yes |
1.30 |
0.08 |
2,433 |
15.79 |
< .0001 | 249.2 | < .0001 |
Noa |
0.00 |
— |
— |
— |
— | |||
| City |
Austin |
0.87 |
0.48 |
2,433 |
1.798 |
0.0723 | 16.07 | < .0001 |
College Station |
0.68 |
0.49 |
2,433 |
1.395 |
0.1630 | |||
Flagstaff |
2.96 |
0.43 |
2,433 |
6.890 |
< .0001 | |||
Milwaukeea |
0.00 |
— |
— |
— |
— |
aReference Level: City = Milwaukee; Beacon Activation = No.
— Not Applicable
Table 177 shows that, overall, more drivers yielded when the beacon was activated (coefficient on logit scale = 1.30) than when it was not activated (coefficient = 0). The table also shows that, overall, the percentage of drivers yielding was lowest in Milwaukee (coefficient = 0) and highest in Flagstaff (coefficient = 2.96).
The predicted yielding rates and their 95-percent confidence limits are shown in table 178 for each site in each city, separately when the beacon was activated or not activated, all other factors held constant. At each site, table 177 shows that the yielding rate is higher when the beacon was activated than when it was not activated (i.e., significant beacon activation effect shown in table 177). Table 178 clearly shows that yielding rates in Flagstaff are considerably higher than in all other cities studied, regardless of whether or not pedestrians activated the device.
From the logistic model, the odds ratio for beacon activation was estimated. Because the interaction between beacon activation and city was not statistically significant, the odds ratio is the same for all cities (and sites in cities). The odds ratios and their 95-percent confidence limits are shown in table 179. In summary, drivers were, overall, 3.68 times more likely to yield when the beacon was activated than when it was not activated.
Table 178. Predicted driver yielding rates by city and site.
Table 179. Odds ratio results for beacon activation.
Factor |
Comparison |
Odds ratio |
Lower 95-percent confidence limit |
Upper 95-percent confidence limit |
Significantly different from 1 at Alpha = 0.05? |
Beacon Activation |
Yes versus No |
3.68 |
3.13 |
4.32 |
Yes |
Influence of Traffic Volume on Driver Yielding
During data collection at pedestrian crossings in the research, data collectors observed that some drivers appeared to make a last-minute decision to yield when a driver in the adjacent lane was yielding, and other drivers appeared to make a last-minute decision not to yield when a driver in the adjacent lane was not yielding. This behavior suggests that driver yielding might be influenced by other vehicles in the traffic stream. It has also been suggested that drivers might be less likely to slow down or stop to yield when there is traffic behind them; that is, when they feel “pushed” from behind. An analysis was conducted to explore whether the presence of other vehicles influenced driver yielding.
The objective of the analysis was to evaluate the relationship between traffic volume and driver yielding rate. To estimate traffic volume for a particular pedestrian crossing, 1-min traffic volume counts were obtained from the videos for a sample of the daytime data collection periods at RRFB sites. The 1-min counts were then aggregated into 5-min averages, but still expressed on a 1-min basis. For example, the 5-min average for a particular minute was the average of the actual count for that minute and the actual counts for the preceding 4 min. Statistics (sample size, minimum, and maximum) for 1-min volume counts at each site are shown in table 180.
Table 180. One-min volume count statistics at crossings with RRFBs.
| City | Site | Number of lanes | Number of crossing events with traffic present | Average of five 1-min volume counts | |
Minimum |
Maximum | ||||
| Austin |
AU-01 |
2 |
37 |
12.0 |
18.8 |
AU-02 |
1 |
74 |
5.4 |
14.2 | |
| College Station |
CS-01 |
1 |
32 |
1.4 |
5.0 |
CS-02 |
2 |
48 |
13.0 |
28.0 | |
| Flagstaff |
FG-01 |
2 |
134 |
17.0 |
36.0 |
FG-02 |
1 |
45 |
13.0 |
25.6 | |
FG-03 |
2 |
32 |
8.8 |
15.8 | |
| Milwaukee |
MK-04 |
2 |
87 |
4.2 |
10.6 |
MK-05 |
2 |
72 |
2.0 |
9.2 | |
MK-06 |
3 |
63 |
10.4 |
18.6 | |
MK-07 |
3 |
41 |
6.2 |
15.4 | |
MK-08 |
2 |
76 |
4.0 |
12.0 | |
The analysis was based on daytime study periods for which traffic counts were obtained (note that only RRFB study sites were considered), at both staged and nonstaged pedestrian crossings. A GLMM with a binomial distribution and logit link was used to model the probability of driver yielding as a function of 1-min traffic volume count (representing the average 1-min count for the nearest 5-min period) and data collection site (to account for potential differences in traffic volume ranges and driver yielding rates between sites). Model estimation was done using PROC GLIMMIX in SAS.
The model showed that percentage yielding decreased as volume increased (slope estimate on the logit scale was -0.02278) but that relationship is not statistically significant (p-value = 0.30) using a type 3 F-test. In other words, there is not enough evidence to conclude that traffic volume influences driver yielding behavior at sites with RRFBs in a positive or negative manner. This is also reflected in figure 101, which presents the plot of predicted driver yielding percentage versus average 1-min volume counts in a 5-min time period, separately for each site; the data points are color-coded by city; different symbols are used for the different sites in a city.
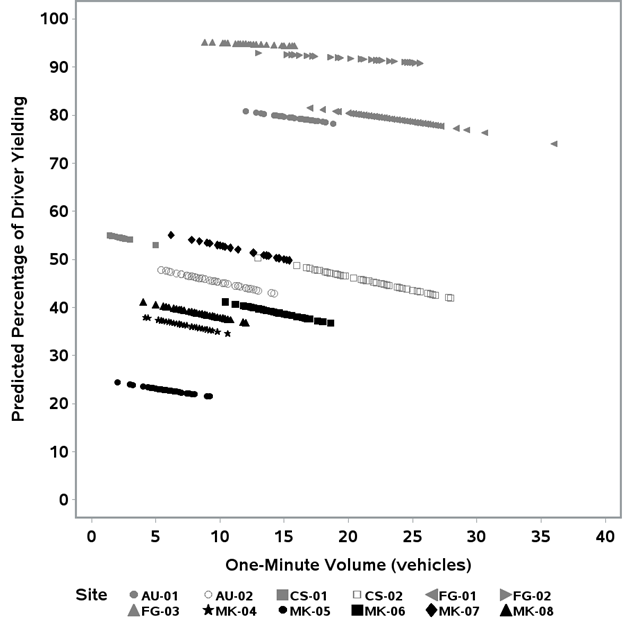
Figure 101. Graph. Predicted percent of driver yielding by 1-min volume counts.

