U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-098 Date: January 2018 |
Publication Number: FHWA-HRT-17-098 Date: January 2018 |
Speed-safety relationships are often described with emphasis on crash frequency, severity outcomes, and various speed metrics. This section of the report briefly describes the relationships between crash severity and operating speed, crash frequency and operating speed, and speed variance and safety performance. The purpose of this section is to describe how the safety performance of a roadway may change as a function of operating speeds.
With regard to crash severity, the operating speed of motor vehicles directly affects the crash outcome. In this case, higher vehicle operating speeds are associated with more severe crashes. This is the result of the kinetic energy dissipated during a crash event. (SWOV 2009) The equation in figure 1 shows the relationship between kinetic energy and speed:
Figure 1. Equation. Relationship between kinetic energy, mass, and speed that occurs during a crash.
Where:
m = mass of object (lbs (kg)).
v = speed of object (ft/s (m/s)).
The kinetic energy is associated with the square of the operating speed; thus, higher operating speeds result in more severe crash outcomes. An example of this relationship was demonstrated by Rosén et al. (2011) in a study of pedestrian fatality risk when struck by a motor vehicle. The authors showed that the fatality risk of pedestrians increases as the impact speed increases. For example, when a vehicle is traveling 24.85 mph (40 km/h), the fatality risk of a pedestrian is approximately 10 percent. However, when a vehicle is operating at 62.14 mph (100 km/h) at the time of impact, the pedestrians fatality risk is approximately 100 percent. Therefore, pedestrians have a greater probability of survival when the impact speed with a passenger car is lower.
The equation in figure 2, developed by Nilsson in 1982, shows the relationship between the expected change in the number of injury crashes as a function of average speed change on roads based on kinetic laws. (SWOV 2009, Elvik 2009)
Figure 2. Equation. Expected number of injury crashes because of a change in the average operating speed. (Nilsson 1982)
Where:
LO2 = number of injury crashes after speed change.
LO1 = initial number of injury crashes (before speed change).
v2 = average speed in the after period (mph or km/h).
v1 = average speed in the before period (mph or km/h).
An increase in the average speed in the after-period is associated with an increase in the expected number of injury crashes after the average speed increase. However, if the after-period average speed decreases, the expected number of injury crashes after the speed change decreases. The exponent in figure 2 can be modified based on the severity outcome considered. The power of 2 shown in figure 2 relates to the number of injury crashes. Changing the power of 2 to a power of 3 can be used to predict the number of severe injury crashes; changing the power to a value of 4 is associated with fatal crashes. (SWOV 2009)
A more recent study by Elvik in 2009, using figure 2 as the basis, produced new exponents that differentiated rural and urban road types when estimating how injury crashes may change as a function of average speed changes. Table 1 lists the various crash severity types and the associated exponents for the rural roads. (SWOV 2009, Elvik 2009)
©SWOV. Reproduced with the express written authority of SWOV. Excerpted from the SWOV
publication T∅ I Report 1034/2009, Institute of Transport Economics T∅I, Oslo, Norway, 2009.
The exponents shown in table 1 can be substituted into figure 3 to predict the number of each crash type after a speed change.
Figure 3. Equation. Expected number of varying crash types as a result of a change in average operating speed.
Where n is the best estimated exponent from table 1.
Similar findings were reported by Kockelman et al. (2006). The study determined that speed limit increases were associated with more severe injuries in a crash. (Kockelman et al. 2006) Table 2 illustrates the change in probability of fatal injuries and the change in fatal injury count as a result of an increase in the posted speed limit.
©TRB. Reproduced with the express written authority of the TRB. Excerpted
from the TRB publication NHCRP Web-Only Document 90 (Project 17-23).
A study by Malyshkina and Mannering (2008) determined the effects of posted speed limit increases on crash severity outcomes, including crashes that occurred on rural country roads, rural State routes, rural city streets, and rural U.S. routes. In general, the authors found that increases in the posted speed limit significantly increased the likelihood a crash would result in an injury or fatality for rural roads. (Malyshkina and Mannering 2008) Table 3 shows the probability of fatal and injury crashes associated with an increase in the posted speed limit.
As shown in table 3, the probability of fatal and injury crashes increases as the posted speed limit increases. In general, the probability of a fatal crash increases more than the probability of an injury crash. For crashes on rural State routes involving cars or light trucks and cars or light trucks, the information in table 3 can be interpreted as follows: A 1-percent increase in the posted speed limit is associated with an 11.9-percent increase in the probability of a fatal crash and a 1.32-percent increase in the probability of an injury crash. (Malyshkina and Mannering 2008) Due to the general increase in the probability of crashes on non-interstate highways, Malyshkina and Mannering (2008) recommended that, when considering potential increases in speed limits on rural roads, each road should be analyzed on a case-by-case basis.
©TRB.
C = cars; LT = light trucks; HT = heavy trucks; (C-LT) + (C-LT) = crash involving a car or light truck and a car or light truck.
—No data.
In summary, higher operating speeds result in crashes that are more severe. If pedestrians are involved in crashes, the fatality risk increases as the impact speed increases. (Rosén et al. 2011) The published literature suggests that, for rural roads, the probability of fatal or injury crashes increases as the posted speed limit increases. (Malyshkina and Mannering 2008)
While the relationship between crash severity and speed is well understood, the relationship between crash frequency and speed is less clear. Intuitively, “if on a road the driven speeds become higher, the crash rate will also increase.” (SWOV 2009) However, the relationship between speed and crash frequency is unknown.
Research by Kockelman et al. (2006) related crash rates and crash frequency to posted speed limits using statistical models. The study found that “crash rates rise with increasing speed limit, but at a decreasing rate,” indicating that the increase in crash rates at higher posted speed limits is less than the increase in crash rates at lower posted speed limits. (Kockelman et al. 2006) Table 4 shows the relationship between higher posted speed limits, average driving speed, and total crash counts based on data from Washington State, Southern California, and Austin, Texas. As shown, the total crash count increases as the speed limit increases, and subsequently, the average driving speeds increase. (Kockelman et al. 2006)
©TRB. Reproduced with the express written authority of the TRB. Excerpted
from the TRB publication NHCRP Web-Only Document 90 (Project 17-23).
Note: Calculations assume average high-speed roadway geometry.
Farmer (2016) reported similar findings to those of Kockelman et al. (2006) in a recent study. The author found that fatality rates and risk increased as maximum speed limits were raised in 41 States. The results indicated that “a 5 mph [8.1 km/h] increase in the maximum state speed limit was associated with an eight percent increase in fatality rates on interstates and freeways and a four percent increase on other roads.” (Farmer 2016)
While studies have revealed the relationship between operating speeds and crash frequency, the exact relationship has not been well quantified. According to Transportation Research Board (TRB) Special Report 254, “speed is also linked to the probability of being in a crash, although the evidence is not as compelling because crashes are complex events that seldom can be attributed to a single factor.” (TRB 1998)
In addition to research on increasing posted speed limits, Donnell et al. (2016) analyzed the effects of setting speed limits lower than engineering recommendations, which are typically set such that they are nearly equal to the 85th-percentile operating speed. The difference between the posted speed limit and the engineering recommended speed limit ranged from 5 to 25 mph (8.1 to 40.3 km/h) at various sites in Montana. The results of the study found that setting the speed limit 5 mph (8.1 km/h) below the recommended engineering value was associated with fewer total and fatal and injury crashes, while setting the posted speed limit 10 mph (16.1 km/h) lower than the recommended engineering value resulted in an increase in fatal plus injury crashes and a reduction in total crash frequency. A statistically significant association between posting speed limits 15 to 25 mph (24.2 to 40.3 km/h) lower than the engineering recommended could not be determined. (Donnell et al. 2016)
A consistent, quantifiable relationship between operating speed and crash frequency has not been reported in the literature. However, research suggests that changing the posted speed limit is associated with changes in the expected crash frequency. Increasing the posted speed limit has resulted in an increase in the expected crash frequency, while reducing the posted speed limit has shown mixed results in past research. Moreover, setting artificially lower posted speed limits may increase the variability in operating speeds among vehicles using two-lane rural highways, which may be associated with higher crash frequencies.
Speed variance often refers to the difference in operating speeds among vehicles on a roadway. Separate studies by Solomon (1964) and Cirillo (1968) concluded that, as vehicle speeds deviated from the average speed of the traffic stream, crash involvement rates increased. Solomon (1964) noted that “as speeds departed from the average speed in either direction, the involvement rate increased in a nearly symmetrical fashion.” The data from Solomon (1964) and Cirillo (1968) are shown in figure 4. The nighttime and daytime curves were developed by Solomon (1964), and the freeway curve was developed by Cirillo (1968).
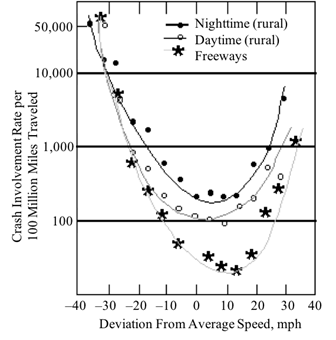
©Stuster et al. (figure 1).
1 mph = 1.60934 km/h.
Figure 4. Graph. Crash involvement rate as speed deviates from average travel speed
from studies by Solomon (1964) and Cirillo (1968). (Stuster et al. 1998, figure 1)
Studies throughout the 1970s produced findings consistent with the research of Solomon (1964) and Cirillo (1968) with regard to speed deviation and crash severity. For example, the Research Triangle Institute, in 1970, studied crashes that occurred on roads with speed limits of 40 mph or higher. (TRB 1998) The results, which were similar to those found in Solomon (1964) and Cirillo (1968), indicated that crash involvement increases as deviation from the average speed increases; however, the magnitude was not as large as found in the previous studies. (TRB 1998)
Similarly, West and Dunn in 1971 attempted to reproduce Solomons curve, while excluding intersection data from the sample. The resulting curve was flatter than Solomons, but it showed that, as speed deviations increase, the crash involvement rate increases. (TRB 1998)
Lave, in 1985, and Garber and Gadiraju, in 1988, produced similar findings. Both studies determined that speed dispersion and crash rates are correlated. Lave (1985) concluded that “speed dispersion significantly related to fatality rates for rural Interstates and rural and urban arterials,” and Garber and Gadiraju (1988) found that “crash rates increased with increasing speed variance on all road classes.” (TRB 1998)
In contrast to the previously determined U-shaped curves, Fildes et al., in 1991, determined a linear relationship between deviations from average travel speeds and crash involvement rates. (TRB 1998)
Davis (2002) concluded that “such positive correlations can be expected in situations where individual crash risk is either an increasing, or a decreasing, or a U-shaped function of speed, and so the correlations in themselves provide no evidence concerning the relation between speed and crash risk for individuals,” and that although “such correlations can be expected in circumstances where individual risk is independent of speed variance, observation of these correlations provides no support for the hypothesis that increases in speed variance increase individual risk.” In other words, Davis (2002) concluded that the study by Solomon (1964) and other studies by researchers who noted similar speed deviation-crash involvement rate relationships were ecological fallacies because individual crash risk based on the speed dispersion among a group of vehicles in the traffic stream does not clearly distinguish between individual and group risk measures.
Based on the findings of the studies summarized in this guidance report, a relationship exists between speed and safety on moderate- and high-speed rural highways. For crash severity, higher vehicle operating speeds are associated with more severe crash outcomes. However, the relationship between crash frequency and speed is not as clear. There is some indication that increasing posted speed limits is associated with an increase in expected crash frequency; however, the relationship between operating speed and crash frequency has yet to be well established.
When applying the self-enforcing design concepts described in chapter 4 of this report, figure 2 and figure 3 may be used to predict how the expected frequency of various crash types may change. To do so, either observed or expected operating speeds for two different conditions can be used to compare the expected safety performance of the two different conditions.