U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-098 Date: January 2018 |
Publication Number: FHWA-HRT-17-098 Date: January 2018 |
Geometric roadway design practices in the United States rely on design controls and criteria set forth in the American Association of State Highway and Transportation Officials (AASHTO) A Policy on Geometric Design of Highways and Streets, also known as the “Green Book.” The design speed is defined in the Green Book as “the selected speed used to determine the various geometric features of the roadway.” (AASHTO 2011) The Green Book either explicitly or implicitly uses the design speed concept to establish horizontal alignment, vertical alignment, and cross-section design elements. Examples include radius of curvature (R), stopping sight distance (SSD), braking distance (db), horizontal sight line offset (HSO), length of vertical curvature (L), maximum superelevation (emax), maximum side friction factor (fmax), and lane and shoulder widths.
For the purposes of this guidance report, the designated design speed of a roadway is the speed established as part of the geometric design process. (Donnell et al. 2009) This speed is used to establish the geometric design criteria noted above and is equivalent to the design speed term used in the Green Book. The inferred design speed, which Donnell et al. (2009) defined as “the maximum speed for which all critical design-speed-related criteria are met at a particular location,” is equivalent to the designated design speed when either minimum or limiting values of design criteria are used. However, the Green Book recommends using design values that exceed minimum values, and in such cases, the inferred design speed will exceed the designated design speed.
Operating speed models have often been used to assess geometric design consistency, most notably on two-lane rural highways. Many studies have estimated statistical models to predict vehicle operating speeds that may be used to evaluate highway design consistency. In many of the models, variables such as roadway geometric features, posted speed limit, and annual average daily traffic (AADT) can be input into the models to determine the vehicle operating speed under free-flow conditions (e.g., vehicle headways of 4 or more sec). While the most common speed output from these models is the 85th-percentile speed, statistical models of mean speed and the standard deviation of speed exist. Applying operating speed models may confirm that designated design speeds, posted speed limits, and driver expectations will all be more consistent when the roadway geometry is designed to manage speeds. (TRB 1998)
The design speed concept does not necessarily guarantee design consistency. The Green Book recommends minimum or limiting values for many speed-based geometric-design elements. When the geometric design values are larger than minimum values, the result is a higher inferred speed, which may be associated with higher operating speeds. This may produce instances where operating speeds on adjacent roadway segments are large or instances when the operating speed differs significantly from the designated design speed used to establish the geometric design features of the roadway. A more detailed explanation of design consistency can be found in later sections of this report.
This chapter examines the relationship between speed and geometric design. The different elements of geometric design, such as horizontal alignment, vertical alignment, and cross-section design elements, are related to speed. The chapter outlines how the designated design speed is related to horizontal- and vertical-curve design criteria, the criteria for selecting cross-section elements, such as lane width, and the relationship between the designated design speed and inferred design speed. The geometric design features of a roadway subsequently influence operating speeds. In addition to discussing how geometric elements are associated with the designated design speed, this chapter describes various operating speed models that have been reported in the literature; this includes mean speed, speed dispersion, and 85th-percentile operating speed. There are examples of how to use operating speed prediction models to evaluate how geometric elements and other roadway characteristics affect driver speed choice. In addition to the illustrative examples shown in this chapter, other speed prediction models are shown in appendix A.
Horizontal curve design is governed by the point-mass model, which prescribes a minimum radius of curvature as a function of the designated design speed, maximum superelevation of the roadway, and maximum side friction factor. (AASHTO 2011) The friction factor used in the geometric design of highways and streets is a demand value that is based on driver comfort thresholds rather than the side friction supply at the tire-pavement interface. The Green Book recommends limiting values for superelevation and side friction factor for horizontal-curve design based on the designated design speed. The radius of curvature equation found in the Green Book is shown in figure 5.
Where:
Rmin = minimum radius of curvature (ft (m)).
V = design speed (mph (km/h)).
emax = maximum rate of roadway superelevation (percent).
fmax = maximum side friction (demand) factor.
Another fundamental geometric design criterion is the SSD, which is the distance needed for a driver to see an object on the roadway in front of the vehicle, react to it, and brake to a complete stop. The SSD is composed of two measures: (1) the distance traveled during perception-reaction time, and (2) the distance traveled during braking. Minimum SSD criteria are based on the assumptions that drivers travel at a speed equal to or below the designated design speed.
The braking distance in the SSD model (criteria) is determined by the formula shown in figure 6, assuming a level vertical grade.
Where:
db = braking distance (ft (m)).
a = deceleration rate (ft/s2 (m/s2)).
In cases where a vertical grade exists, the braking distance is modified as shown in figure 7:
Where G is the grade (rise/run, ft/ft (m/m)).
The braking distance is included as a part of the SSD along with the distance traveled during perception-reaction. The formula shown in figure 8 is used to determine minimum SSD criteria in the Green Book.
Where t is brake reaction time (2.5 s).
Objects located along the inside of horizontal curves may pose a visual sight obstruction, which is also considered in horizontal-curve design. (AASHTO 2011) This is assessed using the HSO, which is determined as follows in figure 9.
Where:
S = stopping sight distance (ft (m)).
R = radius of curve (ft (m)).
While there are numerous statistical models that estimate or predict 85th-percentile operating speeds as a function of geometric design features, as shown in the next section, few models are available to predict mean operating speeds. The mean speed can be used to estimate the 85th-percentile speed, if speeds are normally distributed, by adding the standard deviation of speed to the mean speed. (Roess et al. 2011) This enables the opportunity to assess the association between speed dispersion and geometric design features in a statistical model. This section of the guidance report shows several examples of statistical models that include mean speed and speed dispersion metrics as a function of geometric design features. In each case, the speed metric (i.e., posted speed limit, mean speed, or standard deviation of speed) is the dependent variable, while roadway geometric features and other site-specific features are the independent variables in the model. All of the models are linear models, where the dimension of the independent variable is multiplied by a regression coefficient to determine how the roadway design features influences the expected speed metric. Several other statistical models of vehicle operating speeds are shown in appendix A.
Himes et al. (2011) used a system of linear equations to estimate models for the posted speed limit, mean speed, and standard deviation of speed. An interpretation of the models is provided in table 5. Data were collected on urban and rural two-lane undivided highways in Virginia and Pennsylvania. These data included roadway characteristics, vehicle operating speeds, and hourly traffic flow rates. An example of a typical linear model used by Himes et al. (2011) for their system of simultaneous equations is shown in figure 10. The linear model is used with the information provided in table 5.
Where:
y = speed measure (posted speed limit, mean speed, or speed deviation).
α = intercept for posted speed limit, mean speed, or speed deviation equation.
β = coefficient for road characteristics.
X = road characteristics (geometric features, hourly traffic volume, etc.).
Through the system of equations, the authors could determine the relationship between roadway and roadside features, and traffic flow on posted speed limit, mean speed, and standard deviation. The study found that an increase in posted speed limit and shoulder width was associated with an increase in mean speed. Additionally, Himes et al. (2011) concluded that hourly traffic volume, vertical grade, wooded adjacent land use, and left-hand horizontal curves were negatively associated with speed deviation. The proportion of heavy vehicles was positively correlated with speed deviation. (Himes et al. 2011) Although the simultaneous equations are not shown in this report, the relationship between the dependent and independent variables from the Himes et al. (2011) study are described in table 5 and used in conjunction with the typical linear model shown in figure 10. For example, a 1-ft (0.3-m) increase in the total shoulder width is associated with a 0.33-ft (0.1-m) increase in the expected mean operating speed. These effect sizes are applicable to the range of independent variables included in the sample used to estimate the operating speed models. Readers interested in reviewing the results of the research are encouraged to review the Himes et al. (2011) study.
vph = vehicles per hour.
Similarly, a study by Figueroa Medina and Tarko (2005) estimated statistical models that considered the combined effect of mean speed and speed deviation to predict percentile operating speeds. The free-flow speed models were developed for tangent segments and horizontal curves on two-lane rural highways. The data used to develop the ordinary least squares (OLS) regression model were collected in Indiana and included roadway geometric design features, free-flow speeds, and sight distances. Statistical models were estimated for operating speeds on tangent sections and operating speeds on horizontal curves. The equation shown in figure 11 was developed to predict operating speeds on two-lane rural highway tangent sections.
Where:
Vp = speed on tangent section (mph (km/h)).
TR = percentage of trucks.
PSL50 = equal to 1 if the posted speed limit is 50 mph (80.5 km/h), equal to 0 if the posted speed limit is 55 mph (88.5 km/h).
GR = highway grade (percent).
RES = equal to 1 if the segment has 10 or more residential driveways per mile (1.6 km), 0 otherwise.
SD = available stopping sight distance (ft (m)).
INT = equal to 1 if an intersection is located 350 ft (106.7 m) before or after the spot, 0 otherwise.
PAV = pavement width, includes the traveled way and both paved shoulders (ft (m)).
GSW = total gravel shoulder width (ft (m)).
USW = total untreated shoulder width (ft (m)).
CLR = roadside clear zone, includes the total gravel and total untreated shoulders (ft (m)).
FC = equal to 1 if the spot is located on a flat curve (radius larger than 1,700 ft (518.2 m)), 0 otherwise.
Zp = standardized normal variable corresponding to a selected percentile.
The equation from the Figueroa Medina and Tarko (2005) study used to predict operating speeds on horizontal curves of two-lane rural highways is shown in figure 12.
Figure 12. Equation. Model for speed on horizontal curve roadway sections. (Figueroa Medina and Tarko 2005)
Where:
Vp = speed on horizontal curve section (mph (km/h)).
DC = degree of curvature (degrees).
SE = maximum superelevation rate (percent).
The statistical models shown above consider several roadway characteristics and the posted speed limit to predict the free-flow vehicle operating speeds, which can be used in methods 1 through 4 of the self-enforcing roadway concepts shown in chapter 5. Certain variables in each equation are factors that affect the mean speed or standard deviation of speed. The degree of curvature and superelevation are factors for both mean speed and speed deviation. The variable in the equation containing Zp is associated with the standard deviation. The Z-statistic, which reflects a value representative of a percentile value under the standard normal distribution, is shown in figure 11 and figure 12. This value can be used to predict the percentile speeds. For example, Z50 is equal to 0 for 50th-percentile speeds, and Z85 is equal to 1.036 for 85th-percentile speeds. The interpretations of the variables and parameters for the equations in figure 11 and are shown in table 6.
Drivers select operating speeds based on multiple factors, several of which include the roadway design features. The parameters shown in table 6 generally show that more restrictive geometrics and roadways that have built-up adjacent land use (such as residential and commercial developments) tend to be associated with lower operating speeds.
For tangent segments, the proportion of trucks in the traffic stream, posted speed limit less than 50 mph (80.5 km/h), highway grade, presence of residential driveways, presence of an intersection, and presence of a flat curve are associated with a decrease in mean speeds, while increasing sight distance, pavement width, gravel shoulder width, and untreated shoulder width are associated with an increase in mean speeds. Furthermore, on tangent roadway sections, increasing pavement width and roadside clear zone results in a decrease in speed dispersion, while speed limit, highway grade, and presence of an intersection are associated with an increase in speed dispersion.
For horizontal curves, increased sight distance and the superelevation rates are associated with an increase in mean speed, while presence of residential development, degree of curvature, and the superelevation rate squared is associated with a decrease in mean speed. Additionally, for horizontal curves, the degree of curvature is associated with an increase in speed dispersion, while the superelevation rate is associated with a decrease in speed dispersion.
An example using the models provided by Figueroa Medina and Tarko (2005) and Himes et al. (2011) that estimate mean speed and speed dispersion/deviation is shown in table 7 through table 12. Figueroa Medina and Tarko (2005) determined two distinct models for mean speed and speed dispersion: one for tangent segments, one for horizontal curves. Both are shown in the tables. These examples illustrate how to apply operating speed models to predict driver speed choice on two-lane rural highways. Operating speed prediction models may be used in methods 1 through 4 of the self-enforcing roadway design concepts presented in chapter 5. In table 7 through table 12, the coefficient is multiplied by the dimension to produce a mean speed estimate associated with the dimensions. All these associations are added to produce the predicted mean speed on tangent- or horizontal-curve segments.
—Not applicable.
—Not applicable.
—Not applicable.
—Not applicable.
—Not applicable.
—Not applicable.
vph = vehicles per hour.
As shown in table 7 through table 12, Figueroa Medina and Tarko (2005) and Himes et al. (2011) use different variables to predict mean speeds and speed dispersion. Using the models by Figueroa Medina and Tarko (2005), the mean speed was predicted to be 57.6 mph (92.7 km/h) for tangent segments and 56.5 mph for horizontal curves. Differently, the predicted mean speed using the Himes et al. (2011) model was 52.8 mph (85.0 km/h). Using the models by Figueroa Medina and Tarko (2005), the speed dispersion was predicted to be 5.1 mph (8.2 km/h) for tangent segments and 4.9 mph (7.9 km/h) for horizontal curves. The speed dispersion predicted using the Himes et al. (2011) model was 6.0 mph (9.7 km/h), which is similar to the results from Figueroa Medina and Tarko (2005). One possible explanation for the discrepancies in the results might be the use of different variables across the models. Additionally, the Figueroa Medina and Tarko (2005) models separate tangent segments and horizontal curves.
The 85th-percentile speed represents the speed at which 85 percent of vehicles are traveling at or below under free-flow conditions. This value can be used to establish posted speed limits, as recommended by the Manual on Uniform Traffic Control Devices for Streets and Highways (MUTCD) or to evaluate the design consistency of a roadway. (FHWA 2009) Numerous studies have estimated linear regression models to predict 85th-percentile speeds on horizontal curves and tangents. Several geometric design features as well as the posted speed limit have been included in the speed-prediction models. A summary of these models for two-lane rural highways is provided below. Like the mean and speed dispersion models shown in the previous section of this guidance report, 85th-percentile operating-speed-prediction models can be used to estimate driver speed choice in methods 1 through 4 of the self-enforcing roadway design concepts presented in chapter 5.
Krammes et al. (1995) collected speed and geometric design data along horizontal curves and approach tangents in five States. The data were used to develop a model to predict operating speeds on both curves and approach tangents, and these models were then used to evaluate design consistency between successive geometric features. The geometric features included in the regression models of 85th-percentile operating speed were the degree of curvature, length of curvature, deflection angle, and in some cases, the 85th-percentile speed on approach tangents. The study determined that an increase in the degree of curvature and deflection angle results in a decrease in 85th-percentile speeds on the curve. For curves less than or equal to 4 degrees, as the length of the curve increases, the 85th-percentile speeds on the curve increase, while for curves greater than 4 degrees, as the length of the curve increases, the 85th-percentile operating speeds on the curve decrease. Additionally, as the 85th-percentile speed on the approach tangent increases, the 85th-percentile operating speeds on the curve increase. The equations developed from this study are shown in appendix A.
Fitzpatrick et al. (2000a) collected data on two-lane rural highways in several States to predict the 85th-percentile speed of passenger cars. The 85th-percentile operating speed models are shown in table 33 in appendix A and include the radius of curvature and the rate of vertical curvature. The radius of curvature was found to be the best predictor of operating speeds for horizontal curves on grade, while the rate of vertical curvature was found to be the best indicator of operating speeds on vertical curves that are present on horizontal tangent sections. (Fitzpatrick et al. 2000a) It was determined that the radius of curve significantly affects the 85th-percentile operating speeds on horizontal alignments. When the radius of curve is approximately 820 ft (250 m), 85th-percentile operating speeds decrease sharply, while 85th-percentile speeds on curves with a radius of approximately 2,625 ft (800 m) are similar to the 85th-percentile operating speed on long tangents. (Fitzpatrick et al. 2000a)
Similar to Fitzpatrick et al. (2000a), Misaghi and Hassan (2005) developed models to predict the 85th-percentile operating speed on horizontal curves by considering the radius of curve. Data were collected along 20 horizontal curves of two-lane rural highways in Canada; the data were used to analyze geometric design consistency. (Misaghi and Hassan 2005) Statistical models to predict the speed differential between the approach tangent and the horizontal curve were estimated. The equations developed by Misaghi and Hassan (2005) are shown in appendix A. The study found that an increase in the radius of curvature resulted in an increase in the 85th-percentile speed at the midpoint of the curve and a decrease in the 85th-percentile speed differential. It was also found that as the speed on the approach tangent increases, the deflection angle of circular curve increases, the shoulder width decreases, and the vertical grade increases, the 85th-percentile speed differential also increases. However, as the shoulder width increases, the 85th-percentile speed differential decreased.
Fitzpatrick et al. (2005) and Fitzpatrick et al. (2003) used the posted speed limit on tangent sections of two-lane rural highways to determine the 85th-percentile operating speed using linear regression equations. Both studies determined that geometric design features, including access density and parking along the street, are associated with 85th-percentile operating speeds. The authors also found that the posted speed limit is highly correlated with the 85th-percentile operating speed. (Fitzpatrick et al., 2005) Access density and the presence of parking were negatively correlated with operating speeds. Multiple 85th-percentile speed models were developed for the various road types and included the posted speed limit (i.e., there were separate models for suburban/urban arterial, suburban/urban collector, suburban/urban local, and rural arterial roads). The model developed for rural arterial roadways showed a positive relationship between estimated 85th-percentile operating speeds and the posted speed limit. A 1-mph (1.6-km/h) increase in posted speed limit was associated with a 0.517-mph (0.8-km/h) increase in 85th-percentile speeds for rural arterials. (Fitzpatrick et al. 2003) The equations from Fitzpatrick et al. (2005) and Fitzpatrick et al. (2003) are shown in appendix A.
Schurr et al. (2002) used data collected on rural two-lane highways in Nebraska to predict the 85th- and 95th-percentile operating speeds on rural two-lane highways, which were used to assess design consistency. (Schurr et al. 2002) The speed prediction equations included independent variables such as deflection angle, length of horizontal curve, approach grade, and average daily traffic. The 85th- and 95th-percentile operating speed equations are shown in appendix A. The study concluded that drivers tend to increase operating speeds as the curve is lengthened and 85th-percentile operating speeds decrease as the grade increases. (Schurr et al. 2002)
Lane and shoulder width along with radius of curvature can also affect operating speeds. Lamm and Choueiri (1987) used these variables to develop operating speed prediction models for horizontal curves. Separate regression equations were estimated based on the lane width, which ranged from 10 to 12 ft (3.0 to 3.7 m). “Good” designs were shown to have degree of curvature changes of 5 degrees or less between geometric elements, 85th-percentile speeds that vary less than or equal to 6 mph (9.7 km/h), and radii greater than or equal to 1,200 ft (365.8 m), while “poor” designs had degree of curvature changes larger than 10 degrees, 85th-percentile speeds that vary by more than 12 mph (19.3 km/h), and curve radii less than 600 ft (182.3 m). (Lamm and Choueiri 1987, Lamm et al. 1988) The thresholds for “good” and “poor” designs were based on accident data. Lamm and Choueiri (1987) noted that the average annual daily traffic had little influence on the estimated 85th-percentile operating speed of drivers.
On low-speed, two-lane rural highways in Australia, McLean (1979) estimated OLS linear regression models to predict 85th-percentile operating speeds using variables that included the desired 85th-percentile speed and the curve radius. Comparable to previous studies, it was determined that the curve radius influences the 85th percentile and desired speed of drivers. (McLean 1979) The study determined that an increase in the desired speed is associated with an increase in the 85th-percentile operating speed, and an increase in the inverse curve radius is associated with a decrease in the 85th-percentile operating speed. The 85th-percentile operating speed models from McLean (1979) are shown in appendix A.
While the majority of studies previously described focused on high-speed, two-lane rural roads, Banihashemi et al. (2011) developed operating speed prediction models for low-speed, rural two-lane highways. The posted speed limit ranged from 25 to 40 mph (40.2 to 64.4 km/h). The study estimated regression models to predict 85th-percentile operating speeds on tangents and horizontal curves. One statistical model calculated the 85th-percentile operating speed on a tangent section of roadway using the radius of the preceding curve and the posted speed limit, while another model predicted the 85th-percentile operating speed on a tangent section using the posted speed limit, roadside hazard rating, and the length of the tangent. Additionally, Banihashemi et al. (2011) predicted operating speeds on curves using the radius of curvature. Posted speed limit and length of tangent were found to have a positive association with operating speeds. The radius of the preceding curve, roadside hazard rating, and radius of the subject curve were found to have a negative association with operating speeds. The 85th-percentile operating speed models from Banihashemi et al. (2011) are shown in table 33 in appendix A. These models are also incorporated into the Federal Highway Administration (FHWA) Interactive Highway Safety Design Model (IHSDM) Design Consistency Module (DCM). (FHWA 2016a)
The TRBs Transportation Research Circular E-C151 indicated there is a lack of uniformity between models to predict 85th-percentile operating speeds. (TRB 2011) This can be attributed to the sheer number of models available and the use of many different predictor variables. The circular also states that horizontal curve radius is the only statistically significant variable affecting 85th-percentile operating speeds on alignments containing a horizontal curve. (TRB 2011)
A relationship between the horizontal alignment of a roadway and operating speed is well established. The following section describes the design process for horizontal alignment features and explains how operating speeds are affected by horizontal alignment design features.
To compare the relationship between radius of curvature and 85th-percentile operating speed, equations 1 and 2 by Misaghi and Hassan (2005), equations 1-4 by Fitzpatrick et al. (2000a), and equation 1 by McLean (1979), shown in table 33 in appendix A, from the studies reviewed previously, were used. The resulting plot is shown in figure 13. The vertical axis shows the 85th-percentile operating speeds, while the horizontal axis shows the radius of curvature. Equation 1 from McLean (1979) included the desired speed of the 85th-percentile car (VF) and the curve radius to determine the 85th-percentile speed. The desired speed of the 85th-percentile car is the speed which cars desire to travel based on alignment characteristics of a roadway, including topography, cross section, adjacent land use, and traffic volumes. (McLean, 1979) To accommodate this, the equation was plotted using three different values for VF. The design speed for a given maximum rate of superelevation-minimum radius combination is also shown in figure 13, which is based on table 3-7 of the AASHTO Green Book. (AASHTO 2011)
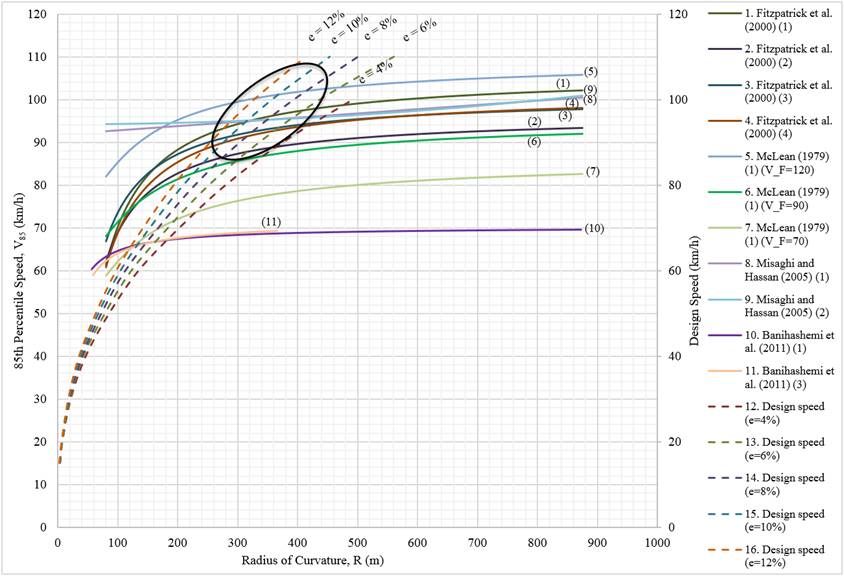
Source: FHWA.
Note: 1 km/h = 0.621371 mph; 1 m = 3.28 ft; in the legend, single numbers that appear in parentheses after the publication year are the equation numbers used from that publication.
Figure 13. Graph. Radius of curvature versus 85th-percentile speeds and design speeds.
As shown in figure 13, there are several speed-inverse radius-of-curvature relationships. The nonlinear portion of the 85th-percentile speed lines show a steep incline when the radius of curvature is small but begin to level as the radius increases. It appears that horizontal curve radii less than 985 ft (300 m) have the greatest influence on vehicle operating speeds. Equations 1 and 3 by Banihashemi et al. (2011) were created for low-speed rural two-lane highways, while the remaining equations were for high-speed, two-lane rural highways.
In figure 13, the area approximately within the black oval represents the range in which design speeds and operating speeds are similar. For very sharp curves, the geometry of the roadway tends to influence the operating speed of vehicles. Depending on the superelevation of the road, horizontal curvature tends to have little effect on operating speeds when the radius of curvature is approximately 1,480 ft (450 m) or larger. Readers interested in the association between the radius of curve and the expected number of crashes on two-lane rural highways should refer to the AASHTO Highway Safety Manual (HSM). (AASHTO 2010)
Equation 1 by Krammes et al. (1995) and equations 2, 4, 6, and 8 by Lamm and Choueiri (1987) were plotted to show the relationship between the degree of curvature and 85th-percentile operating speeds in figure 14. Lane widths were considered in three of the equations: the Lamm and Choueiri (1987) (equation 4) model is applied for 10-ft (3.0-m) lane widths, the model by Lamm and Choueiri (1987) (equation 6) is applied for 11-ft (3.4-m) lane widths, and the model by Lamm and Choueiri (1987) (equation 8) is applied for 12-ft (3.7-m) lane widths.
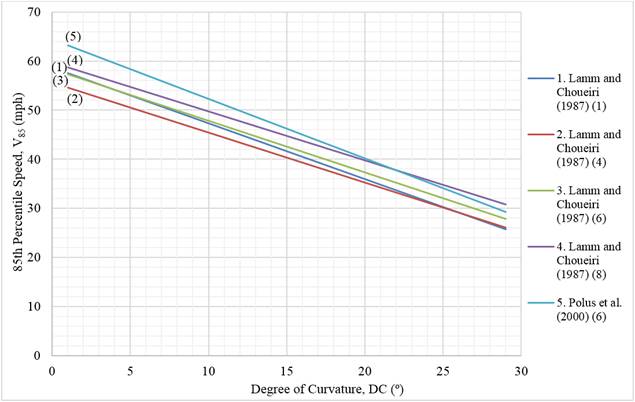
Source: FHWA.
Note: 1 mph = 1.60934 km/h; in the legend, single numbers that appear in parentheses after the publication year are the equation numbers used from that publication.
Figure 14. Graph. Degree of curvature versus 85th-percentile speeds.
Figure 14 shows that as the degree of curvature increases, the 85th-percentile operating speed decreases. As the lane width increases, the 85th-percentile operating speed correspondingly increases.
Polus et al. (2000) estimated statistical models of 85th-percentile operating speeds on tangent segments of two-lane rural highways by considering the horizontal curve radii of distal and proximal curves (previous and following curves). For long tangent lengths that exceed 492 ft (150 m), the geometric measure of the tangent section and adjacent curves is represented in the model in figure 15, which is then used in one of the speed prediction equations shown in figure 17.
Figure 15. Equation. Geometric measure of tangent section and attached curves for long tangent length.
Where:
GML = geometric measure of tangent section and attached curves for long tangent length (ft2 (m2)).
R1, R2 = previous and following curve radii (ft (m)).
TL = tangent length (ft (m)).
t = selected threshold for tangent length (ft (m)).
For short tangent lengths, defined as less than 492 ft (150 m), the geometric measure of the tangent section and adjacent curves is represented in the equation in figure 16, which can then be used in the speed prediction model shown in figure 18.
Where GMs is the geometric measure for short tangent lengths (ft (m)).
The 85th-percentile speed prediction equations developed by Polus et al. (2000) are shown in table 33 in appendix A. Speed prediction equations developed by Polus et al. (2000) (equations 1-6 in their report) which contain the variable GML, are shown in figure 17. As the values for GML increase, the 85th-percentile speeds increase. There are limitations on each equation for values of GML, tangent length, and radius of curvature that are noted in appendix A. The tangent length is kept constant in all equations. The two radii used are not specified; however, the product of the two radii in the equation for GML is increasing as the 85th-percentile speeds are increasing.
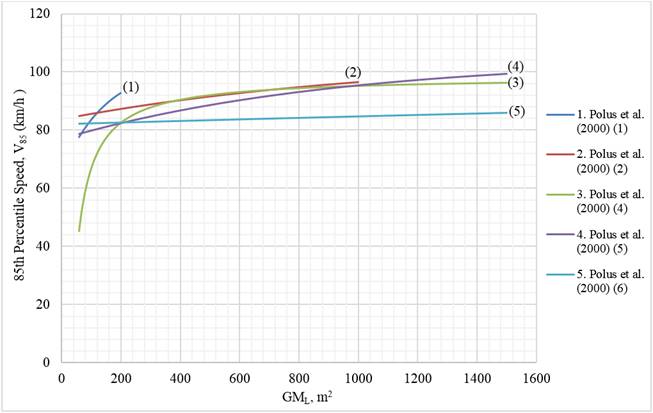
Source: FHWA.
Note: 1 km/h = 0.621371 mph; 1 m2 = 10.7639 ft2; in the legend, single numbers that appear in parentheses after the publication year are the equation numbers used from that publication.
Figure 17. Graph. Geometric measure for long tangent lengths and attached curves versus 85th-percentile speeds.
Similar to the equations containing the variable GML, the equation by Polus et al. (2000) (equation 3) is illustrated in figure 18. While this equation is used for short tangent lengths (less than 492 ft (150 m)), as GMs increases, so does the 85th-percentile operating speed. A larger GMs indicates that the sum of both radii is larger. The tangent length is not factored into the equation for GMs due to its small value.
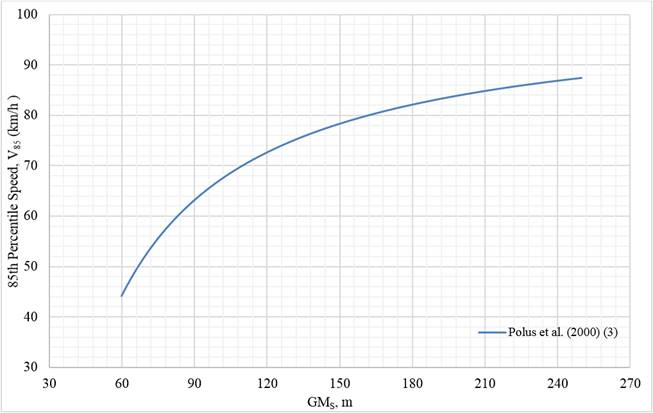
Source: FHWA.
Note: 1 km/h = 0.621371 mph; 1 m = 3.28 ft; in the legend, the single number that appears in parentheses after the publication year is the equation number used from that publication.
Figure 18. Graph. Geometric measure of short tangent section versus 85th-percentile speeds.
The following statistical model from Polus et al. (2000), as shown in figure 19, was used to generate the speed-tangent relationship:
Where SP equals the 85th-percentile speed (km/h) (1 km/h = 0.621371 mph).
This model is illustrated using a superelevation of 12 percent and a minimum radius of curvature for R1 and R2 for each designated design speed shown in figure 20, which is based on information in the Green Book. (AASHTO 2011) Additionally, each minimum radius of curvature for R1 and R2 was multiplied by 1.5 to show the effects of choosing larger-than-minimum radii on the speed-tangent length relationship.
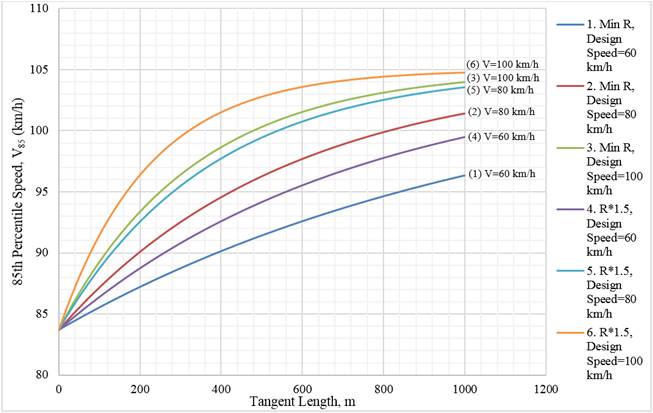
Source: FHWA.
Note: 1 km/h = 0.621371 mph; 1 m = 3.28 ft.
Figure 20. Graph. Tangent lengths versus 85th-percentile speeds for e = 12 percent.
As shown in figure 20, as tangent lengths between two horizontal curve radii increase, the 85th-percentile speeds increase. The shape of the curves shows a higher rate of change for tangent lengths and 85th-percentile speeds up to a certain tangent length, after which the influence of the tangent length on operating speed diminishes. Tangent lengths tend to significantly affect operating speeds until approximately 1,310 ft (400 m), at which point the tangent length does not have a substantial effect on speeds. When the designated design speed is higher (e.g., 62.14 mph (100 km/h)) the curves in figure 20 are sharper than at lower design speeds. Additionally, the 85th-percentile operating speeds are larger for curves with larger radii than curves with smaller radii.
There is a relationship between the vertical alignment of a roadway and design and operating speeds. The following section describes the vertical alignment design process and shows how the designated design speed is associated with the vertical alignment design elements. The section also illustrates how vertical alignment design decisions are associated with operating speeds. This information can be used to identify vertical alignment dimensions that produce operating speeds consistent with the designated design speed and posted speed limit along the roadway.
Similar to horizontal curves, sight distance on crest vertical curves must also be considered in the geometric design of highways and streets. Sight distance for vertical curves pertains to the drivers ability to see the road ahead when the vertical features of the roadway change. (AASHTO 2011) The minimum length of the vertical curve considers the algebraic difference in grades, SSD, height of the drivers eye above the roadway surface, and the height of an object above roadway surface. Crest vertical curve design is indirectly related to the designated design speed through SSD criteria.
There are two different models that may be used to determine the minimum length of crest vertical curves, depending on the relationship between the SSD and vertical curve length. The model used to determine the crest vertical curve length when the sight distance is less than the length, according to the Green Book, is as shown in figure 21.
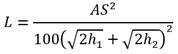
Figure 21. Equation. Crest vertical curve length when sight distance is less than the vertical curve length.
Where:
L = length of vertical curve (ft (m)).
A = algebraic difference in grades (percent).
S = sight distance (ft (m)).
h1 = height of eye above roadway surface (ft (m)).
h2 = height of object above roadway surface (ft (m)).
When the sight distance is greater than the vertical curve length, the model is as shown in figure 22.
Figure 22. Equation. Crest vertical curve length when sight distance is greater than the vertical curve length.
The length of sag vertical curves is affected by headlight sight distance. Sag vertical curves consider the algebraic difference in grades and headlamp beam distance. According to the Green Book, the headlamp beam distance is “the distance between the vehicle and point where the 1-degree upward angle of the light beam intersects the surface of the roadway.” (AASHTO 2011) The length of sag vertical curve is indirectly related to the designated design speed of the roadway via the SSD.
Figure 23 through figure 26, which are from the Green Book, illustrate the computations needed to determine the length of a sag vertical curve for various stated conditions. (AASHTO 2011)
When the headlamp beam distance is less than the length of the sag vertical curve, the equation from either figure 23 or figure 24 is used.
Figure 23. Equation. Length of sag vertical curve when headlamp beam distance is less than the length. (AASHTO 2011)
Figure 24. Equation. Length of sag vertical curve when headlamp beam distance is less than the length-reduced equation. (AASHTO 2011)
When the headlamp beam distance is greater than the length of the sag vertical curve, the equation from either figure 25 or figure 26 is used.
Figure 25. Equation. Length of sag vertical curve when headlamp beam distance is greater than the length. (AASHTO 2011)
Figure 26. Equation. Length of sag vertical curve when headlamp beam distance is greater than the length reduced equation. (AASHTO 2011)
When equations 5 and 6 by Fitzpatrick et al. (2000a) were plotted to illustrate the relationship between rate of vertical curvature and 85th-percentile operating speeds, as shown in figure 27, the shape resembles the relationship between horizontal radius of curvature and 85th-percentile operating speed. The graphed equations for 85th-percentile speed were compared to the design speed based on the rate of vertical curvature for SSD from table 3-34 in the AASHTO Green Book. (AASHTO 2011) The design speeds are shown on the right (secondary) vertical axis of figure 27.
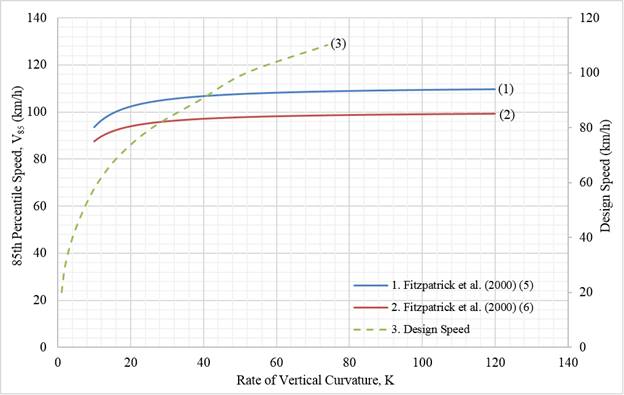
Source: FHWA.
Note: 1 km/h = 0.621371 mph; in the legend, single numbers that appear in parentheses after the publication year are the equation numbers used from that publication.
Figure 27. Graph. Rate of vertical curvature versus 85th-percentile speeds and design speeds.
Equation 5 by Fitzpatrick et al. (2000a) was used to plot the speed-vertical curve relationship in figure 27 for vertical curves with limited SSD on horizontal tangents, while equation 6 by Fitzpatrick et al. (2000a) was used for sag vertical curves on horizontal tangents with limited sight distance. (Fitzpatrick et al. 2000a) Both show a sharp increase in 85th-percentile operating speeds when the rate of vertical curvature is between approximately 10 and 29, and then the slope of the graphic increases slowly as the rate of vertical curvature increases. Additionally, when the recommended minimum rates of vertical curvature are used, there is a greater influence on the 85th-percentile speeds for both SSD and passing sight distance.
There is no well-documented relationship between roadway cross-section elements and operating speeds on rural two-lane highways. However, the designated design speed of the roadway is associated with several cross-section elements on two-lane rural highways. Cross-section elements can include, but are not limited to, shoulder widths, lane widths, number of lanes, and roadside features. The following section describes the design process for cross-section features and discusses operating speed models that show predicted operating speeds based on the various designed cross-section elements.
Cross-section elements that are related to the designated design speed of a roadway include lane width, number of lanes, shoulder widths, and roadside features. According to the Green Book, the roadway is defined as “a portion of a highway, including shoulders, for vehicular use.” (AASHTO 2011) Driving behavior, such as the selection of speeds, is influenced by the cross-sectional elements of a roadway. This section of the report describes how the designated design speed is related to cross-section dimensions, particularly on two-lane rural highways.
The roadway width and the number of lanes are dependent on the designated design speed and design volumes. (AASHTO 2011) The number of lanes is also influenced by the target level of service and capacity requirements. (AASHTO 2011) The roadway width may also vary if accommodating the presence of bicyclists. The Green Book provides guidance for the minimum traveled-way widths for rural arterials that are determined through the designated design speed and design volume. It also states minimum widths of usable shoulders based on design volumes. (AASHTO 2011)
The Green Book offers general guidance for lane width dimensions, which range from 9 to 12 ft (2.7 to 3.7 m), based on the roadway type and traffic volume. (AASHTO 2011) On high-speed, high-volume roadways, 12-ft (3.7-m) lanes are recommended. Lane widths of 10 ft (3.0 m) can be used on low-speed roadways, while a 9-ft (2.7-m) width may be used on low-speed, low-volume roadways. (AASHTO 2011) Table 13 and table 14 show the Green Book recommended minimum traveled-way widths for rural arterials, based on the designated design speed and design volume. (AASHTO 2011) As shown in table 13 and table 14, lane widths of 11 or 12 ft (3.4 or 3.7 m) are recommended, depending on the designated design speed and design volume.
According to the Green Book, “a shoulder is the portion of the roadway contiguous with the traveled way that accommodates stopped vehicles, emergency use, and lateral support of subbase, base, and surface course.” (AASHTO 2011) Shoulders can be paved or unpaved. Shoulder width design guidance varies depending on the functional class and planned use of the shoulder. According to the Green Book, shoulder widths are typically 12 ft (3.7 m) for higher speed roads with high traffic volumes and a significant truck proportion among the traffic, typically referring to freeways, while 6-ft (1.8-m) shoulders are more common on low-volume roads. Table 14 shows the recommended minimum width of the usable shoulder for all design speeds based on design volumes. Shoulder widths of 4 to 8 ft (1.2 to 2.4 m) are recommended on rural arterials.
The roadside is the area beyond the shoulders and is considered part of the cross section. AASHTOs Roadside Design Guide offers guidance for the design of roadside features (specifically, clear-zone distances) based on the designated design speed and design average daily traffic. (AASHTO 2011) Higher design speeds require larger clear zones. Additionally, the clear-zone requirements also increase as the design average daily traffic increases. Typically, steeper foreslopes and backslopes are associated with wider clear-zone recommendations. Readers interested in the association between cross-section elements and the expected number of crashes on two-lane rural highways should refer to the AASHTO HSM. (AASHTO 2010)