U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-10-035 Date: September 2011 |
Publication Number: FHWA-HRT-10-035 Date: September 2011 |
Until the advent of the Superpave™ mix design system in the early 1990s, the viscosity of asphalt binders was the key measure used in purchase specifications. As a result, many sections that are now reaching their design lives and, as a result, are included in the LTPP database, contain various measures of viscosity. Over the years, four primary types of viscosity measures have been adopted: (1) ring and ball temperature (R&BT), (2) penetration (at various temperatures), (3) absolute viscosity at 140 °F (60 °C), and (4) kinematic viscosity at 275 °F (135 °C). These measures have been used together or separately in various grading schemes. With the exception of penetration, these viscosity measures are beyond the range of temperature conditions typically needed for modulus prediction. As a result, a certain amount of processing the available data is necessary. In this appendix, the steps necessary to properly analyze available viscosity data are presented.
Although the relationship between viscosity and temperature is highly nonlinear, it has been found that when proper transformations are made to temperature and viscosity, a linear relationship exists. This relationship is commonly referred to as the “A-VTS relationship.”(43) This relationship is shown schematically in figure 79 and mathematically in equation 56. The plateau region in figure 79 is based on arguments that are, in turn, based on the chemical structure of asphalt binder and suggest that the maximum viscosity for asphalt binder is 2.7 x 1012 cP (0.0027 x 1012 Pas).(44) For the purposes of this report, this same limiting criterion was also adopted.
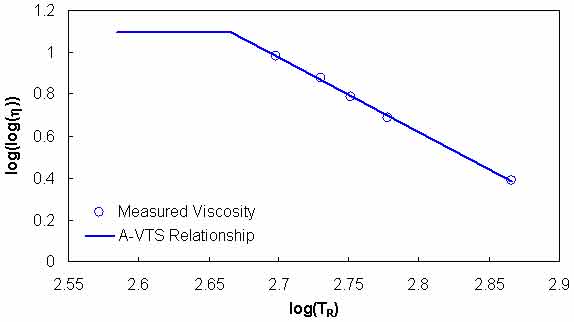
Figure 79. Graph. A-VTS relationship.
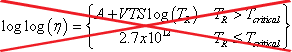 |
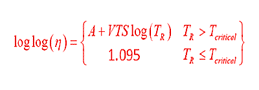 |
(56) |
Where:
| η | = | Viscosity (cP). |
|---|---|---|
| A | = | Intercept of temperature susceptibility relationship. |
| VTS | = | Slope of temperature susceptibility relationship. |
| TR | = | Temperature in Rankine. |
| Tcritical | = | Temperature in Rankine at which the viscosity is equal to 2.7 x 1012 cP (0.0027 x 1012 Pas). |
Because the A-VTS relationship is linear, only two of the four viscosity measures are needed to completely characterize the relationship. The following sections provide the equations necessary to convert the four measures to actual viscosity.
The softening point of asphalt binder as measured by AASHTO T53-08 is also known as R&BT.(45) According to literature on the topic, this temperature, measured in Fahrenheit, corresponds to the temperature at which asphalt binder has a viscosity of 13,000 P (1,300 Pas).(44)
The penetration number for asphalt binder is determined via AASHTO T49-07.(46) In this test, a 3.5-oz (100-g) needle is used to penetrate an asphalt sample for 5 s. The amount of penetration, measured in tenths of a millimeter, is the penetration number for the asphalt binder at the particular test temperature. The measurement temperature typically used for specification purposes is 77 °F (25 °C); however, other temperatures, including 39.2 and 115 °F (4 and 46 °C), may also be measured. Penetration values are converted to viscosity using the relationship suggested by Mirza and Witczak as seen in equation 57:(44)
| (57) |
Where:
| η | = | Viscosity (P). |
|---|---|---|
| PEN | = | Penetration number at a given test temperature. |
The absolute viscosity is the viscosity of asphalt binder measured at 140 °F (60 °C) by AASHTO T202-03.(47) Because this quantity is typically reported in poise instead of centipoise, the only conversion needed is to multiply the given quantity by 100.
The kinematic viscosity of asphalt binder is determined at 275 °F (135 °C) via AASHTO T201-03.(48) Kinematic and absolute viscosities are related by the density of the medium under investigation. The relationship between these two quantities is shown in equation 58. For LTPP purposes, it is assumed that the density for all binders is equal to 0.6 oz/in3 (1.03 g/cm3).
| (58) |
Where:
| η | = | Absolute viscosity (cP). |
|---|---|---|
| ν | = | Kinematic viscosity (cSt). |
| ρ | = | Density (oz/in3 ((g/cm3)). |
For a given asphalt binder, the following properties are measured:
| R&BT temperature | = | 104 °F (40 °C) |
|---|---|---|
| PEN at 39.2 °F (4 °C) | = | 19 |
| PEN at 77.0 °F (25 °C) | = | 156 |
| η | = | 774 P (77.4 Pas) |
| ν | = | 266.1 centistokes (cSt) |
Using these relationships, the viscosity is computed for different temperatures as follows:
| 39.2 °F (4 °C) | = | 4.14 × 109 cP (0.00414 × 109 Pas) |
|---|---|---|
| 77.0 °F (25 °C) | = | 3.66 × 107 cP (0.00366 × 107 Pas) |
| 104 °F (40 °C) | = | 1.30 × 106 cP (0.0013 × 106 Pas) |
| 140 °F (60 °C) | = | 7.74 × 105 cP (0.00774 × 105 Pas) |
| 275 °F (135 °C) | = | 2.74 × 102 cP (0.00274 × 102 Pas) |
After performing linear regression on these quantities, it is found that A = 10.599, VTS = -3.5646, and Tcritical = 464.8 °R.
As part of the NCHRP 1-37A effort, researchers compiled typical A and VTS values for different purchase specification grades.(2) These typical values include Superpave™ PG binders, AC viscosity-graded binders, and penetration-graded binders. Data were not compiled for all grades in use across the United States, but most grades were included. Because some of the LTPP layers fell in the category where the only binder information known was the grade, these relationships are considered important. In table 36, the A and VTS parameters are presented for the different grades reported in the MEPDG documentation.(2)
| Asphalt Binder Grade | A | VTS | Asphalt Binder Grade | A | VTS |
|---|---|---|---|---|---|
| PG 46-34 | 11.5040 | −3.9010 | PG 70-28 | 9.7150 | −3.2170 |
| PG 46-40 | 10.1010 | −3.3930 | PG 70-34 | 8.9650 | −2.9480 |
| PG 46-46 | 8.7550 | −2.9050 | PG 70-40 | 8.1290 | −2.6480 |
| PG 52-10 | 13.3860 | −4.5700 | PG 76-10 | 10.0590 | −3.3310 |
| PG 52-16 | 13.3050 | −4.5410 | PG 76-16 | 10.0150 | −3.3150 |
| PG 52-22 | 12.7550 | −4.3420 | PG 76-22 | 9.7150 | −3.2080 |
| PG 52-28 | 11.8400 | −4.0120 | PG 76-28 | 9.2000 | −3.0240 |
| PG 52-34 | 10.7070 | −3.6020 | PG 76-34 | 8.5320 | −2.7850 |
| PG 52-40 | 9.4960 | −3.1640 | PG 82-10 | 9.5140 | −3.1280 |
| PG 52-46 | 8.3100 | −2.7360 | PG 82-16 | 9.4750 | −3.1140 |
| PG 58-10 | 12.3160 | −4.1720 | PG 82-22 | 9.2090 | −3.0190 |
| PG 58-16 | 12.2480 | −4.1470 | PG 82-28 | 8.7500 | −2.8560 |
| PG 58-22 | 11.7870 | −3.9810 | PG 82-34 | 8.1510 | −2.6420 |
| PG 58-28 | 11.0100 | −3.7010 | AC-2.5 | 11.5167 | −3.8900 |
| PG 58-34 | 10.0350 | −3.3500 | AC-5 | 11.2614 | −3.7914 |
| PG 58-40 | 8.9760 | −2.9680 | AC-10 | 11.0134 | −3.6954 |
| PG 64-10 | 11.4320 | −3.8420 | AC-20 | 10.7709 | −3.6017 |
| PG 64-16 | 11.3750 | −3.8220 | AC-3 | 10.6316 | −3.5480 |
| PG 64-22 | 10.9800 | −3.6800 | AC-40 | 10.5338 | −3.5104 |
| PG 64-28 | 10.3120 | −3.4400 | PEN 40-50 | 10.5254 | −3.5047 |
| PG 64-34 | 9.4610 | −3.1340 | PEN 60-70 | 10.6508 | −3.5537 |
| PG 64-40 | 8.5240 | −2.7980 | PEN 85-100 | 11.8232 | −3.6210 |
| PG 70-10 | 10.6900 | −3.5660 | PEN 120-150 | 11.0897 | -3.7252 |
| PG 70-16 | 10.6410 | −3.5480 | PEN 200-300 | 11.8107 | −4.0068 |
| PG 70-22 | 10.2990 | -3.4260 | — | — | — |
|
— Indicate that no additional relationships exist. |
|||||