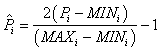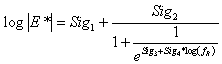U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

 
REPORT
This report is an archived publication and may contain dated technical, contact, and link information
Back to Publication List        
Publication Number:  FHWA-HRT-10-035    Date:  September 2011
Publication Number: FHWA-HRT-10-035
Date: September 2011

 

LTPP Computed Parameter: Dynamic Modulus

APPENDIX D: ANN MODEL FACTORS

D.1 INTRODUCTION

The ANN model developed herein contains a mapping ANN architecture and is based on supervised learning. In the developed network, the learning method used is a feed forward back propagation, which is one of the best known types of ANN models. The sigmoidal function, which is shown in equation 101, was chosen as the transfer function. After an indepth investigation of network configurations, it was found that the three–layer network with equal nodes in the first two layers is the most appropriate configuration. All three ANN models share some basic functions, which are shown in equations 101–105. Equations specific to the MR ANN are equations 106–108, and equations specific to the GV ANN and VV ANN models are equations 109–111. For equations 101–111, it should be understood that when a single index is used, it indicates an array. When dual indices are used, they represent a matrix with the first letter indicating the values in the row and the second letter indicating the values in the column. Index i represents the number of input parameters, index k represents the number of nodes in the first hidden layer, and index j represents the number of nodes in the second hidden layer. For the MR ANN, l represents the number of output values. All inputs are scaled to have a value between −1 and 1. The normalization equation is shown in equation 112. Also, note that the MR model produces coefficients for the sigmoidal function and is provided in equation 113. The units of the prediction are in megapascals as compared to pounds per square inch, which has been used elsewhere in this report.

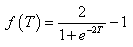Equation 101. Definition of sigmoidal transfer function used in ANN model. f parenthesis T end parenthesis equals 2 divided by the sum of 1 plus exponential of the product of superscript −2 times T, all minus 1. (101)
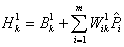Equation 102. Definition of vector H for the value of the nodes at the first hidden layer. H superscript 1subscript k equals B subscript k, superscript 1 plus the summation from i equals 1 to m of the product of matrix W for W superscript 1subscript ik and vector P for the normalized value for given input variable i, P hat subscript 1. (102)
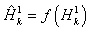Equation 103. Definition of vector H hat for the transferred value of the nodes at the first hidden layer. H hat superscript 1 subscript k equals f times parenthesis H superscript 1 subscript k end parenthesis. (103)
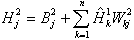Equation 104. Definition of vector H for the value of the nodes at the second hidden layer. H superscript 2 subscript j equals B superscript 2 subscript j plus the summation from k equals 1 to n of the product of H hat superscript 1 subscript k and matrix W for W superscript 2 subscript kj. (104)
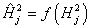Equation 105. Definition of vector H hat for the transferred value of the nodes at the second hidden layer. H hat superscript 2 subscript j equals f times parenthesis H superscript 2 subscript j end parenthesis. (105)
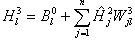Equation 106. Definition of vector H for the value of output node. H superscript 3 subscript l equals B superscript 0 subscript l plus the summation from j equals 1 to n of the product of vector H hat for H hat superscript 2 subscript j and matrix W for W superscript 3 subscript jl. (106)
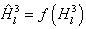Equation 107. Definition of vector H hat for the transferred value of the output node. H hat superscript 3 subscript l equals f parenthesis H superscript 3 subscript l end parenthesis. (107)
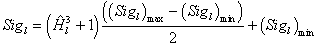Equation 108. Definition of trained output for MR ANN model. Sig subscript l equals the sum of parenthesis H hat superscript 3 subscript l plus 1 end parenthesis, parenthesis parenthesis Sig subscript l end parenthesis subscript max minus parenthesis Sig subscript l end parenthesis subscript min end parenthesis, divided by 2, all plus parenthesis Sig subscript l end parenthesis subscript min. (108)
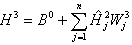Equation 109. Definition of vector H for the value of the output node. H superscript 3 equals B superscript 0 plus the summation from j equals 1 to n of the product of H hat superscript 2 subscript j and matrix W for W superscript 3 subscript j. (109)
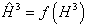Equation 110. Definition of vector H hat for the transferred value of the output node. H hat superscript 3 equals f times parenthesis H superscript 3 end parenthesis. (110)
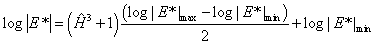Equation 111. Definition of trained output for VV and GV ANN models. The logarithm base 10 of vertical line E superscript star vertical line equals the sum of parenthesis H hat superscript 3 plus 1 end parenthesis times parenthesis the logarithmic base 10 of vertical line E superscript star vertical line subscript max minus the logarithmic base 10 of vertical line E superscript star vertical line subscript min end parenthesis divided by 2, all plus the logarithmic base 10 of vertical line E superscript star vertical line subscript min. (111)

Where:

T = The placeholder variable.
f(T) = The transfer function.
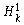Value of the nodes at the first hidden layer = The value of the nodes at the first hidden layer.
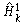Transferred value of the nodes at the first hidden layer = The transferred value of the nodes at the first hidden layer.
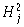Value of the nodes at the second hidden layer = The value of the nodes at the second hidden layer.
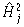Transferred value of the nodes at the second hidden layer = The transferred value of the nodes at the second hidden layer.
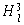Value of output node l (MR ANN) 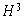= The value of output node l (MR ANN).
Value of the output node (GV ANN and VV ANN) 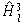= The value of the output node (GV ANN and VV ANN).
Transferred value of the output node l, normalized output (MR ANN) = The transferred value of the output node l, normalized output (MR ANN).
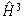Transferred value of the output node, normalized output (GV ANN and VV ANN) = The transferred value of the output node, normalized output (GV ANN and VV ANN).
Pi = The input variables.
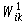Weight factors for the first hidden layer = The weight factors for the first hidden layer.
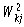Weight factors for the second hidden layer = The weight factors for the second hidden layer.
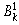Bias factors for the first layer 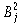= The bias factors for the first layer.
Bias factors for the second layer = The bias factors for the second layer.
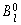Bias factors for the outer layer (MR ANN) = The bias factors for the outer layer (MR ANN).
B0 = The bias factor for the outer layer (GV ANN and VV ANN).
(Sigl)max = Maximum value for sigmoidal coefficient l in the trained data (MR ANN).
(Sigl)min = Minimum value for sigmoidal coefficient l in the trained data (MR ANN).
log |E*|max = Maximum log|E*| of the trained data (GV ANN and VV ANN).
log |E*|min = Minimum log|E*| of the trained data (GV ANN and VV ANN).
m = The number of nodes in the first hidden layer (see table 21).
n = The number of nodes in the second hidden layer (see table 21).
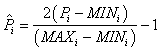Equation 112. Definition of normalized value for given input variable. P hat subscript i equals the product of 2 times parenthesis P subscript i minus MIN subscript i end parenthesis divided by parenthesis MAX subscript i minus MIN subscript i end parenthesis, all minus 1. (112)

Where:

Pi = Given input variable, i.
Normalized value for given input variable, i 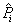= Normalized value for given input variable, i.
MINi = Minimum value of i in calibration dataset.
MAXi = Maximum value of i in the calibration dataset.
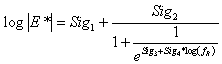Equation 113. Definition of trained output for VV and GV ANN models. The logarithm base 10 of vertical line E superscript star vertical line equals Sig subscript 1 plus Sig subscript 2 divided by the sum of 1 plus 1 divided by the exponential of superscript Sig subscript 3 plus Sig subscript 4 times the logarithmic base 10 of parenthesis f subscript R end parenthesis. (113)

Where:

fR = Reduced frequency (hertz).
Sig1 = First sigmoidal function coefficient.
Sig2 = Second sigmoidal function coefficient.
Sig3 = Third sigmoidal function coefficient.
Sig4 = Fourth sigmoidal function coefficient.

Three ANN models have been developed from this architecture: (1) MR ANN, (2) VV ANN, and (3) |G*| ANN. In the following sections, the value of the weight factors, bias factors, input parameters, and normalization parameters are given for each of these models.

D.2 MR ANN

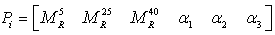Equation 114. Input variable vector for resilient modulus based model in terms of mixture properties. P subscript i equals 1x6 vector where the vector element is equal to parenthesis M superscript 5subscript R, M superscript 25 subscript R, M superscript 40 subscript R, alpha subscript 1, alpha subscript 2, and alpha subscript 3 end parenthesis. (114)

Where:

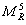Resilient modulus at 41° F (5 °C), MPa = Resilient modulus at 41 °F (5 °C) (megapascals).
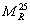Resilient modulus at 77° F (25 °C), MPa = Resilient modulus at 77 °F (25 °C) (megapascals).
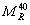Resilient modulus at 104° F (40 °C), MPa = Resilient modulus at 104 °F (40 °C) (megapascals).
α1 = Shift factor coefficient 1 (0.0007).
α2 = Shift factor coefficient 2 (-0.1646).
α3 = Shift factor coefficient 3 (0.806).
Table 50. Wik1 matrix elements for MR ANN (part 1).
Element k Element i
1 2 3
1 -0.00200156589300513 0.00128692125170315 0.00284438217881075
2 0.28516256606761700 0.49118675435971600 -0.01820933290109810
3 -0.13012155717600300 0.07853842949381770 0.17680064334424700
4 -0.29231959611729100 0.17617282979184900 0.39775504273252700
5 -1.41445013310154000 6.44297995264973000 -1.77482643703439000
6 -0.21241167223734400 0.12821712282974400 0.28884600944520300
7 0.03400370099657090 -0.02101635307328680 -0.04672053052579720
8 0.09548185985586570 -0.05752189953709870 -0.13026426280596500
9 0.32507208708348800 -0.19505459789439700 -0.44164369167303300
10 0.28899439562768500 1.14183643175563000 1.48347522466600000
11 -0.98864001747551200 -2.86851244653187000 -3.23450809016547000
12 1.62092571912098000 -4.58381702398853000 2.21293392742914000
Table 51. Wik1 matrix elements for MR ANN (part 2).
Element k Element i
4 5 6
1 -712.8628402976380000 9.83219882009042000 -1.94319401017490000
2 753.53741515309100000 7.67671366971338000 -0.84350062295273200
3 -1093.068754047720000 9.23892947309088000 0.14382032104724800
4 -1129.557247424060000 -1.50590848559491000 -0.66955349262730300
5 -1.83158558608035000 3.97456523446851000 7.12208818273337000
6 -839.5292060420890000 8.73889517406220000 0.67603083268390200
7 755.74883976821200000 -12.71270279414850000 -1.34117207352107000
8 847.61568238744000000 -12.59290188069720000 -0.47503813284310300
9 410.33781806362100000 -7.80175950866107000 -2.36148957427579000
10 -805.5026910683050000 -4.21610143211805000 4.07885029040178000
11 471.04240973832900000 13.45559381618210000 -3.61642908665572000
12 28.37591023338010000 12.28550446563640000 0.70805040715617700

Table 52. Bk1 vector elements for MR ANN (transposed for convenience).

Element k B1
1 6.17091399170251000
2 7.71811183199239000
3 5.04220257285617000
4 1.36211474573909000
5 1.27586815658043000
6 1.24112853958781000
7 -0.55920953360997600
8 -1.54793233282465000
9 -2.38955526082692000
10 -5.31749985483251000
11 6.04452696422904000
12 2.43088472177158000
Table 53. Wkj2 matrix elements for MR ANN (part 1).
Element
j		 Element k
1 2 3 4
1 -1.27212265453448000 0.98941325757367200 -1.90058367559899000 -1.69308092227318000
2 2.24917988742036000 -1.47046066978322000 2.81430927085362000 2.35680695833274000
3 0.90938132410845800 -1.87010703846175000 1.72113608938929000 0.53365095186003000
4 0.71420875730581000 -2.02463155580309000 1.24092642037176000 -0.75971225627055200
5 1.02573805084948000 -5.05227027803185000 -0.50811201125450400 0.12398342947210100
6 2.87344198982080000 1.1825109019882500 1.83686226283920000 1.07343492432610000
7 -6.84673965801500000 8.75898275822440000 -6.07092164029969000 -5.61770119661654000
8 -0.27215636118304200 -0.71265020644285800 0.10337231975487200 -0.50732389147556800
9 -1.24280778319817000 -0.42688724228155600 -1.49197352443203000 -1.1916709449455000
10 -0.87186156614646800 -0.55253243107747700 0.01014336151285740 -1.38109064819317000
11 5.05262125180162000 -3.58899791830666000 5.32477118646701000 6.08771475391962000
12 1.94315627250074000 -11.72058718677100000 1.02780825311488000 -0.07727872946434780
Table 54. Wkj2 matrix elements for MR ANN (part 2).
Element j Element k
5 6 7 8
1 1.72171850082868000 -1.22361303255407000 0.26380146379060500 1.59052924999161000
2 -0.69983955029987400 2.15750218152474000 -2.72092291591448000 -2.56417332772541000
3 5.68303374707809000 -0.22567435819557400 -0.38683461689596400 -1.33743701004047000
4 -5.29792907293055000 -0.79868120409271800 0.56639895589096100 -0.15145370730044200
5 -6.9600412768491900 -0.25943738604012600 -0.07507398274261910 -0.60082153969042900
6 -6.90406457489009000 0.66048638607472900 -0.74734595052120800 -1.77757048725853000
7 14.28996210073420000 -4.93956480500064000 5.47678679301124000 5.04474379279507000
8 5.33401793234324000 -0.67814558115517500 1.35435682469839000 0.67517616517050400
9 6.13017525412482000 -0.25895030883091000 0.76688050726348400 0.59567627875874100
10 -4.52656667316437000 -0.61198000964802400 0.66990865283891800 1.79648574970781000
11 61.00473788943800000 5.94808205391293000 -6.49782178526526000 -5.63585227166289000
12 -0.74313876146962200 -0.49502882731012100 -0.04343884290084600 0.43382323116577400
Table 55. Wkj2 matrix elements for MR ANN (part 3).
Element j Element k
9 10 11 12
1 1.28982526693395000 -1.36139827942535000 0.81242090814931100 0.75421177520166000
2 -1.98856516178736000 2.88665638759158000 -2.22345527946482000 47.32908703710720000
3 -1.46019991113224000 0.83288304533622300 -0.18737329755176000 7.94189735755131000
4 -0.62488286109702500 0.99358597783727000 -1.80707863873754000 -1.51697406306899000
5 -0.53491093234660500 0.03718852912964090 0.50412006696695100 -2.27324267108375000
6 -1.75495744905123000 0.04848011387017500 0.65137190325020200 -19.45130367879080000
7 6.34621810767813000 -4.33945264323816000 8.48179242696090000 -55.79280738270100000
8 -0.02703184429355360 -1.38007437316169000 -2.03641139073515000 7.15173377918400000
9 0.18219945071653500 -0.43950447308134000 0.88864139595275200 17.00276947159220000
10 0.18331101506990700 -1.29082311881848000 0.17907218849290100 0.00442335303199802
11 -4.70890802094776000 5.58102070625218000 -4.42512396747533000 34.44356640107110000
12 -0.58348656053904200 11.76004227042600000 -18.62573141905100000 40.36522874277380000

Table 56. Bj2 vector elements for MR ANN (transposed for convenience).

Element j B2
1 0.69029100571690900
2 24.78083328475230000
3 -14.21641765871200000
4 0.59454387354854500
5 0.83441149973420900
6 2.00770642875969000
7 -6.80461833224959000
8 -3.04506035154618000
9 -2.81699338543501000
10 -0.01908957707522740
11 -23.82659200096020000
12 -2.84950882850698000
Table 57. Wjl3 vector elements for MR ANN (part 1).
Element l Element j
1 2 3 4
1 1.55631817035049000 -6.71717964044816000 5.52866041884021000 -23.13533591138010000
2 -2.10815560445854000 5.53651802240772000 -4.20046449739353000 13.84767577640070000
3 10.42186407217690000 1.07658778061795000 -1.00952254919933000 1.35728376824998000
4 12.53270054290200000 -2.82666156182142000 0.36140292673336200 11.63883002692080000
Table 58. Wjl3 vector elements for MR ANN (part 2).
Element l Element j
5 6 7 8
1 7.89233240566186000 3.41508482981355000 0.23067944090008000 -6.35835335516061000
2 -4.35253958227055000 -4.33105623723765000 -0.23450370767118300 4.90555584894330000
3 -0.53624851772844700 4.26302489876063000 0.18477243720173400 0.95437352582270800
4 -5.27378018192719000 12.58074218873790000 0.30883922900382400 -0.81566323458280500
Table 59. Wjl3 vector elements for MR ANN (part 3).
Element l Element j
9 10 11 12
1 3.12448098517872000 7.76943031096589000 0.16915092735543200 17.81482352191000000
2 -4.10144987129725000 -8.41207948330685000 -0.13394241862122600 -14.80599826102690000
3 4.33224573662362000 -12.80943716195050000 0.05065733872668660 -2.21601216037733000
4 12.62825381229430000 2.74268434100584000 0.08908525498240080 8.18232817352028000

Table 60. Normalization parameters for MR ANN.

Parameter Maximum Minimum
MR5 (MPa) 34053.0 4800.3
MR25 (MPa) 15411.0 1081
MR40 (MPa) 6863.7 378.9
α1 (1/ °C2) 0.002400 -0.000194
α2 (1/ °C) -0.098 -0.300
α3 1.430 0.490
Sig1 (MPa) 2.660 -0.043
Sig2 4.700 1.500
Sig3 4.100 0.650
Sig4 0.850 0.260

 

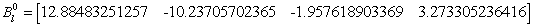Equation 115. The bias factors for the outer layer vector for resilient modulus based model in terms of coefficient values. B superscript 0 subscript l equals 1x4 vector where the vector element is equal to parenthesis 12.88483251257, −10.23705702365, −1.957618903369, and 3.273305236416 end parenthesis. (115)

D.3 VV ANN

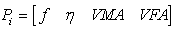Equation 116. Input variable vector for viscosity based model in terms of binder and mixture properties. P subscript i equals 1x4 vector where the vector element is equal to parenthesis f, eta, VMA, and VFA end parenthesis. (116)

Where:

f = Frequency, Hz.
η = Viscosity, 109 P (108 Pas).
Table 61. Wik1 matrix elements for VV ANN.
 Element k Element i
1 2 3 4
1 0.00275807935276415 9.65414347487492000 2.03545176382323000 9.60483606710040000
2 0.00699289293419363 23.57848634613580000 -14.68700301452580000 -7.85111160151172000
3 -29.85518987292190000 -0.01748605711868700 -0.05226790767927880 0.10630299509262800
4 0.00272712204182532 0.22756591526942600 -0.44128805965281300 0.51123020782505100
5 0.00885326169582901 2.81905088512526000 -16.74274657827420000 -11.51343150553350000
6 -0.00604496464330366 -3.83323067510033000 -3.76213295881730000 -4.29370215749809000
7 0.00001271343965432 178.92786633284100000 -0.00411385898011919 0.00960133688419267
8 0.01990111297026090 -1.16149781971796000 3.28168963629711000 7.53282726564379000
9 0.01005974523187870 -0.39351960943073500 -2.51237935759967000 -4.29116433585095000
10 2.20552340599479000 -0.04056518032735070 0.20605359978971700 0.15739161949478100
11 -0.02404084443474640 -6.58972054945535000 -0.71981980149770700 1.52555084062215000
12 -0.00480809655510197 -0.27885745601162500 0.20260632406742000 -0.77108867937747000
13 0.00078471111967578 28.44415144259920000 -0.87571840373706600 1.95186725224564000
14 0.00771761131363787 5.33676984624904000 -11.97622550219350000 7.71358914882133000

Table 62. Bk1 vector elements for VV ANN (transposed for convenience).

Element k B1
1 15.74835436269630000
2 12.95405722517280000
3 -32.89896917533040000
4 -1.10052248959346000
5 -10.78091133520380000
6 -6.05302142493261000
7 179.14709718593800000
8 0.65710599534106200
9 0.97891317883012100
10 4.72223785338294000
11 -6.55165918673815000
12 0.16731428319782600
13 27.93047751952220000
14 -1.37408939580495000
Table 63. Wkj2 matrix elements for VV ANN (part 1).
 Element j Element k
1 2 3 4
1 0.10511744512798600 0.10087889704665500 -6.08319321387257000 -6.59951922338895000
2 0.48485201906871100 -0.98061150567901500 5.28213726518926000 -0.99307488071221600
3 0.38666686767509600 0.14407696249404200 -0.64821237624430900 -0.68553604874521800
4 -0.29103025921087400 -0.12300943951262000 0.20660407620275500 0.84431006573009900
5 7.20145641626984000 151.58382852395500000 -35.04225274891410000 50.31324421340920000
6 57.80869276380200000 45.53819717827600000 34.31952056143690000 24.37102641478090000
7 0.04766296493976920 -0.00042062272941119 -1.64780015541921000 -0.14767680975504800
8 1.33157778260189000 -0.00864139577441407 -10.53694387134640000 -28.77316964591470000
9 0.95432357054777500 -1.02389021831262000 46.82499405300610000 61.27640626961720000
10 0.09476608746471290 -0.04013797559617900 15.08416115539120000 1.26248388850460000
11 0.65673641456535000 25.30163159128400000 6.86855242012598000 52.55865424871390000
12 -57.90977231272230000 57.64668837199080000 -36.95301005956680000 -51.19423424496710000
13 2.27010107107278000 -2.76393198240337000 14.26953262603660000 20.57219630346000000
14 -0.81442427169913900 -1.58075985235425000 20.32130385637230000 -21.37864285760230000
Table 64. Wkj2 matrix elements for VV ANN (part 2).
Element j Element k
5 6 7 8
1 0.10958125840908900 0.17103742786951300 7.53738934561000000 0.32157150848996400
2 1.10538840213556000 -0.06005243494707140 -0.46816179656466200 -0.11362528740921000
3 -0.03668587237246070 -0.20195215673052800 0.50583875586658800 0.04117830356601680
4 0.04165310223654260 0.12412276818401500 -0.71560911337291800 -0.06643717805416860
5 -135.8256006242760000 4.39896372970834000 2.12048232621756000 1.61468697764029000
6 12.18509505034930000 4.51309256843370000 7.19546156774681000 11.77248078904480000
7 0.00470501377909039 -0.00810109614328989 -0.20468271977533900 -0.00831305598572143
8 0.14429797312686300 0.32443645525838900 -18.31175213933740000 -0.17988695146765000
9 0.48668670982841300 -1.06169701219564000 -0.47416257725070700 2.01336853261287000
10 0.02124957257916830 -0.01491154156235320 214.20333131224300000 0.05344273444888970
11 -16.55295761437330000 31.36367340855210000 0.14069168225602600 20.67506639536700000
12 105.32395565518000000 -68.59510275333000000 -0.57180295407110300 24.60816018017130000
13 3.20913352965092000 -1.46922615656989000 -0.45618908696155800 -0.74587534667358800
14 2.14653394183588000 2.86656902371875000 -1.38951291360800000 1.51498306935364000
Table 65. Wkj2 matrix elements for VV ANN (part 3).
Element j Element k
9 10 11 12
1 0.67436953255572400 1.52993707048353000 -1.56378559364968000 -5.97316328323617000
2 0.83884786099458000 0.72056843262828500 0.33823343591634200 0.32995739963357400
3 0.13129904885190400 0.03393257336078320 -0.33495422276929500 1.21059369021165000
4 -0.08374413143914640 -0.14011290475212000 0.40330307484415800 -0.92068329846481200
5 -4.74183346589286000 -7.18458646900432000 -8.20175738069755000 21.46322182793860000
6 -2.22050947171933000 -3.19929780229875000 43.60123067158340000 -38.15447962643450000
7 0.04970822735474000 0.38186826752702800 0.02975701201504030 -0.07187684022207080
8 18.96102127708150000 0.34577779423701500 0.10112166202643200 -4.34637124684574000
9 136.10585968855900000 3.75489444791017000 5.73368672918881000 35.37279289616110000
10 -0.36747370936357000 1.90705035404089000 -1.42366525777415000 6.11736464999887000
11 -20.86114381473210000 4.50957253702840000 0.73758107479932900 -3.21435115847231000
12 -19.00772620196210000 44.26713771722670000 38.62379852233980000 -1.87378784809568000
13 0.17584310006536200 3.18528344468959000 0.62107582578786300 8.04752096583409000
14 2.97468553092343000 -4.21086927843771000 2.73490619946452000 -3.67293829703328000
Table 66. Wkj2 matrix elements for VV ANN (part 4).
Element j Element k
13 14
1 -1.12245731810529000 0.67867713986347200
2 0.41929338131065000 -1.37665914977400000
3 0.58160889599262400 0.36777315706927400
4 -0.51666057998473900 -0.35135512626691600
5 3.27948738968729000 1.94926465685885000
6 -45.89506402313440000 70.49683570639200000
7 0.01612131389179630 -0.01152122049407600
8 3.77564707007114000 -4.91896963383303000
9 3.89920658003942000 -49.40155143998830000
10 2.24644797717875000 -0.11299018277251500
11 -9.63227261518900000 -119.1073499783990000
12 -41.84530118313840000 -35.82982088240670000
13 0.56754251531620400 -3.01209559093347000
14 2.43256581696669000 -1.47837832821775000

Table 67. Bj2 vector elements for VV ANN (transposed for convenience).

Element j B2
1 -12.23193846569030000
2 0.61294509854138200
3 -2.26121589380006000
4 1.99708243932415000
5 22.07400990717020000
6 -31.86954422722210000
7 -2.41399982513437000
8 -55.27590960198670000
9 -106.0101552356340000
10 -30.89403826224180000
11 -76.24782342311330000
12 69.28157710468700000
13 20.21945409941280000
14 6.12083493792229000

Table 68. Wj3 vector elements for VV ANN.

Element j W3
1 1.15373219918479000
2 -6.43559921490721000
3 -27.68360314597900000
4 -29.84574981371640000
5 -0.19407309170597600
6 0.11995708036519800
7 37.96893504107600000
8 34.00719477253400000
9 0.43014683810727000
10 58.47886817741680000
11 11.94908594315590000
12 -0.07969689689272150
13 1.28313108040340000
14 0.53296310828566400

Table 69. Normalization parameters for VV ANN.

Parameter Maximum Minimum
Frequency (Hz) 25 0.01
Viscosity (109 P) 1.99 x 10-6 27.00
VMA (percent) 34.64 9.51
VFA (percent) 95.07 32.82
|E*| (psi) 6.77 3.52

 

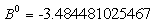Equation 117. The bias factor for the outer layer for viscosity based model in terms of coefficient value. B superscript 0 equals −3.484481025467. (117)

D.4 |G*|-BASED ANN (GV ANN)

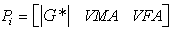Equation 118. Input variable vector for binder shear modulus based model in terms of binder and mixture properties. i, P subscript i equals to 1x3 vector, where the vector element is equal to parenthesis vertical line G superscript star vertical line, VMA, and VFA end parenthesis. (118)
Table 70. Wik1 matrix elements for GV ANN.
Element k Element i
1 2 3
1 -0.00024607061578008 0.39573112252617300 0.03137522820868100
2 0.06369415599503260 1.20396485280366000 -0.41366999743116300
3 0.12560166488947000 12.23092512080170000 -15.40428508265840000
4 144.78479285235900000 0.03602175009356860 -0.01486430375847190
5 -0.88590000706402800 -6.64620868848810000 6.76784019433308000
6 -0.24480066614146600 -175.126570586870000 110.38396928012700000
7 0.35658487276453800 -1.13633711409192000 -2.69698652853612000
8 0.05160380299493010 0.96914775793747200 -0.45058047297787600
9 -0.11763211836169300 -2.07308576925671000 0.85862809150608600
10 -0.10260986412141000 -1.89647330970902000 0.63576557888985500
11 0.83832125440623900 5.01864835388400000 -7.07830843630593000
12 -22.27016740128570000 2.82680472067850000 -1.10402495920697000

Table 71. Bk1 vector elements for GV ANN (transposed for convenience).

Element k B1
1 -13.23020275429390000
2 -1.15912963101547000
3 4.49668100338684000
4 144.90818089626700000
5 0.92374996199841500
6 187.12386013330800000
7 -0.64852041864182200
8 0.79297555520979200
9 1.27505357580263000
10 1.56260322810567000
11 -1.80964836750601000
12 -24.23180989095970000
Table 72. Wkj2 matrix elements for GV ANN (part 1).
 Element j Element k
1 2 3 4
1 1.68662477353906000 0.81911931325403900 -0.03005180291517210 0.00569345005879186
2 -4.86360723468991000 105.69622449695400000 -2.47849339660309000 0.18455777935409300
3 91.15855920616590000 92.66954611901590000 -40.91260113059330000 -1.67503899696897000
4 106.61660556715000000 22.90152433894880000 229.56133863086000000 -0.21741320127254800
5 0.73120568649091500 -2.04683544732935000 0.02907899740128110 -0.00680956721358145
6 20.01334655907270000 -124.1136850495880000 -12.93483076443820000 0.16320420801843400
7 11.03261781901980000 -55.35942281688430000 -0.25840813426995300 2.36249059396197000
8 6.30522135450740000 -72.37646707852670000 -2.13173103347156000 23.41004001398310000
9 -34.10766755925970000 26.04890333595410000 0.13622620891216500 -534.4781944799400000
10 -18.68321667137760000 103.90356571837300000 -2.46159833726818000 0.18433171253622200
11 19.14302423015890000 3.59998964741180000 0.25399603119775500 -44.54673896061580000
12 -0.33713658604817700 12.87184727785630000 0.13134300289504600 6.54659549746008000
Table 73. Wkj2 matrix elements for GV ANN (part 2).
Element j Element k
5 6 7 8
1 0.01859496903873790 7.79141326044631000 0.01459371336584290 -4.01406752777277000
2 30.71090633980400000 5.37671972945662000 3.18886351743859000 -2.85108340883822000
3 87.71359895456880000 -77.08967734352910000 22.84350940748950000 335.75204711704400000
4 68.74692689690920000 -45.87194063996940000 12.79313464511960000 -37.77625414085690000
5 -0.0094809359102436 -1.94014227142969000 -0.01256576806807960 4.16910051124176000
6 -37.35043967525970000 5.27365300784224000 1.31038988899583000 43.16167413535480000
7 91.10288269578740000 -29.48793850026970000 -0.04849305692638800 3.23868144074583000
8 3.53501265914675000 0.83322882269153700 1.62246929641914000 6.69105720723216000
9 -0.09814064912135180 -0.02099590067358970 -0.19796523923434900 17.65358100702660000
10 55.61599363732450000 -5.35164182127019000 3.15862176137102000 -2.82977620499617000
11 -0.30334853272738200 43.07269450273440000 -0.22059949976226000 1.05780537005262000
12 0.11377535318423100 0.11441693675638400 0.15289220845030100 -1.13970260089778000
Table 74. Wkj2 matrix elements for GV ANN (part 3).
Element j Element k
9 10 11 12
1 3.47596025162077000 -3.82827454649034000 0.01169888530415500 0.12954405222771200
2 94.55869709663890000 -7.34809568152935000 10.41344790169180000 21.32866301200200000
3 205.23211172111800000 -34.98627953103440000 76.29312010940660000 -30.59094661558560000
4 64.60376447639590000 -21.68091976305070000 66.41011966659030000 -26.22110679142560000
5 0.08966925765449130 -0.90205636358616400 -0.00585495017589258 0.00011267457317091
6 12.38797404837280000 -96.26501641581090000 -37.17032464251540000 0.12957951502862800
7 -50.14112337006290000 -8.38137267965061000 40.93959435883270000 -0.32474898284932000
8 -55.82517744922910000 -57.75954730123160000 2.17269724264550000 -54.42459642341290000
9 -1.13861767294711000 6.61476050123734000 0.25450956423993600 -1.38236982388117000
10 93.41332136138760000 -9.48311646261710000 49.01504550800940000 20.79054924536240000
11 2.55740586147654000 2.61695086136455000 -0.09940520779407240 3.00291187179692000
12 4.67064477635346000 8.20560279728423000 0.10724854309492400 3.33502620583327000

Table 75. Bj2 vector elements for GV ANN (transposed for convenience).

Element j B2
1 -3.02263601315923000
2 5.97704828771739000
3 -91.56648216379910000
4 -106.5989770883490000
5 -0.36740268358330700
6 -20.04954785032860000
7 -10.42449435680280000
8 -5.32258083806398000
9 32.81032420706510000
10 17.56993360741350000
11 -20.65675932973890000
12 2.35956011260892000

Table 76. Wj3 vector elements for GV ANN.

Element j W3
1 -134.7651195030360000
2 92.96416099463190000
3 0.07847134028534860
4 0.58725325729413100
5 -146.9138139427070000
6 -12.15444670634670000
7 34.34304769221520000
8 -63.09541362586340000
9 -76.62381419958460000
10 -93.21865080014820000
11 -29.95120632059920000
12 0.71757242259101300

Table 77. Normalization parameters for GV ANN.

Parameter Maximum Minimum
|G*| (psi) 676,000 0.0293
VMA (percent) 22.21 9.51
VFA (percent) 95.07 32.82
|E*| (psi) 6.81 3.52

 

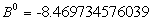Equation 119. The bias factor for the outer layer for binder shear modulus based model in terms of coefficient value. B superscript 0 equals −8.469734576039. (119)

 

 

 

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse | U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101