U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-11-045 Date: November 2012 |
Publication Number: FHWA-HRT-11-045 Date: November 2012 |
As identified in chapter 1, the primary motivation for this research was to identify candidate binder parameters to replace the current Superpave® PG specifications, with special emphasis on fatigue cracking. This chapter describes the development background of various parameters that were identified and gives examples and the quantitative ranking of the ALF binders included in the study.
ALF binder test results from the standard specification test (AASHTO T 315) using DSR to control fatigue cracking at the intermediate temperature range is provided in table 62.(5) Both the specification temperature and the loss modulus at the fixed ALF loading temperature of 66 °F (19 °C) are provided. The unmodified asphalt is the stiffest, and SBS 64-40 modified binder is the softest, with the SBS-LG, CR-TB, and terpolymer modified binders in between.
|
Binder |
|G*|sinδ Value at 19 °C, 10 radians/s, 0.4 Percent Strain, |
Temperature at |G*|sinδ = 5 MPa, |
|---|---|---|
|
PG70-22 |
12,100,000 |
26.0 |
|
Air blown |
6,810,000 |
22.6 |
|
SBS-LG |
4,060,000 |
18.1 |
|
CR-TB |
4,210,000 |
17.9 |
Terpolymer |
2,610,000 |
14.3 |
CR-AZ |
— |
11.9 |
|
SBS 64-40 |
1,761,800 |
8.6 |
1 Pa = 0.000145 psi
°F = 1.8(°C) + 32
— Indicates data were not measured.
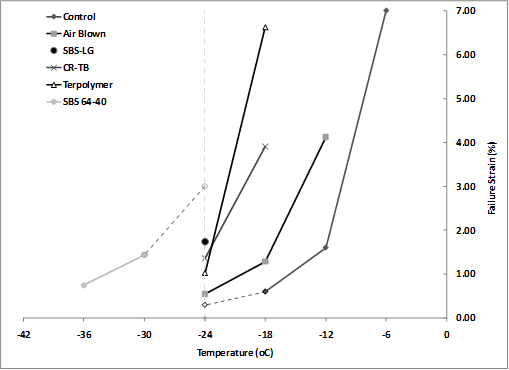
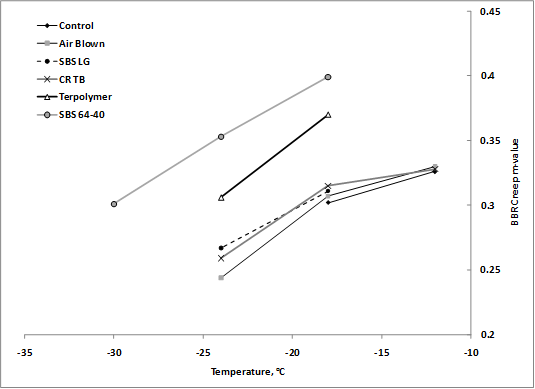
Low-temperature failure stress and strain (brittle fracture) from the ALF binders measured in the standard specification test (AASHTO T 314) using the DT test are provided in table 63 along with the BBR creep m-values (AASHTO T 313).(4,3) Failure stress has much less of a trend with temperature than failure strain, and thus failure strains are shown graphically in figure 106, where two of the binders’ failure strains were extrapolated to a common temperature of -11 °F (‑24 °C). The rankings of the binders’ failure strains from smallest to largest are PG70-22, air blown, terpolymer, CR-TB, SBS-LG, and SBS 64-40. The creep m-values show the PG70-22, air-blown, SBS-LG, and CR-TB binders have very similar response, while the terpolymer and SBS 64-40 binders have a notably larger, more compliant response (see figure 107).
|
Binder |
DT + BBR Critical Temp. (°C) |
Continuous Low Temp. Grade (°C) |
DT and BBR Test Results |
||||||
|---|---|---|---|---|---|---|---|---|---|
|
Category |
-6 °C |
-12 °C |
-18 °C |
-24 °C |
-30 °C |
-36 °C |
|||
|
PG70-22 |
-22.4 |
-23 |
Failure strain (%) |
7.00 |
1.61 |
0.60 |
0.30* |
— |
— |
|
Failure stress (MPa) |
6.35 |
5.00 |
4.38 |
— |
— |
— |
|||
|
m-value |
— |
0.326 |
0.302 |
— |
— |
— |
|||
|
Air blown |
-27.1 |
-28 |
Failure strain (%) |
— |
4.12 |
1.29 |
0.55 |
— |
— |
|
Failure stress (MPa) |
— |
4.43 |
4.89 |
4.76 |
— |
— |
|||
|
m-value |
— |
0.330 |
0.307 |
0.244 |
— |
— |
|||
|
SBS-LG |
-33.7 |
-28 |
Failure strain (%) |
— |
— |
— |
1.75 |
— |
— |
|
Failure stress (MPa) |
— |
— |
— |
6.99 |
— |
— |
|||
|
m-value |
— |
— |
0.311 |
0.267 |
— |
— |
|||
|
CR-TB |
-32.9 |
-28 |
Failure strain (%) |
— |
— |
3.91 |
1.36 |
— |
— |
|
Failure stress (MPa) |
— |
— |
4.88 |
5.74 |
— |
— |
|||
|
m-value |
— |
0.328 |
0.315 |
0.259 |
— |
— |
|||
|
Terpolymer |
-31.1 |
-31 |
Failure strain (%) |
— |
— |
6.63 |
1.03 |
— |
— |
|
Failure stress (MPa) |
— |
— |
5.42 |
5.88 |
— |
— |
|||
|
m-value |
— |
— |
0.370 |
0.306 |
— |
— |
|||
|
SBS 64-40 |
-36.0 |
-38 |
Failure strain (%) |
— |
— |
— |
3.00* |
1.44 |
0.75 |
|
Failure stress (MPa) |
— |
— |
— |
— |
6.56 |
6.17 |
|||
|
m-value |
— |
— |
0.399 |
0.353 |
0.301 |
— |
|||
°F = 1.8(°C) + 32
1 MPa = 145 psi
— Indicates data were not measured.
*Semilog extrapolation.
°F = 1.8(°C) + 32
Figure 106. Graph. Failure strain of ALF binders in the low-temperature DT test versus temperature.
°F = 1.8(°C) + 32
Figure 107. Graph. BBR creep m-value of ALF binders versus temperature.
Multiple cycle oscillatory fatigue tests are a classical technique. Such tests impose repeated stresses and strains below the material’s single-cycle strength limit, and the net effect is that damage accumulates, causing the modulus to decrease and the material to ultimately fail. This characterization technique in the DSR was identified in NCHRP 9-10 research for further exploration and implementation as an asphalt binder fatigue parameter.(20)
Martono and Bahia conducted stress sweep and time sweep fatigue testing on the ALF binders in the DSR.(65) Time sweeps are cyclic tests where the imposed oscillatory strain amplitude is fixed throughout the test and fatigue damage is exhibited as the resultant peak-to-peak stresses decrease and, thus, the modulus decreases. A drawback to the time sweep is that it can require many cycles and a significant amount of time before fatigue failure can be reached, which is not ideal for routine specification testing. As the name suggests, a stress sweep consists of multiple cycles of imposed stress magnitude causing the resultant cyclic strain to increase and the modulus to decrease. A special variation of stress sweep fatigue testing was developed by Martono and Bahia as a faster alternative to the time sweep.(65) Instead of fixing the stress amplitude during the test, the stress was exponentially increased to bring failure sooner. A schematic of the two tests is shown in figure 108.
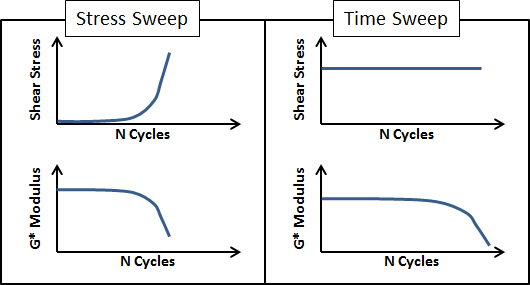
Figure 108. Graph. Typical observations during stress sweep and time sweep tests.
Martono and Bahia conducted time sweeps at three strain levels at 66 °F (19 °C) and 10 Hz.(65) The results are summarized in table 64. The binder was RTFO-aged only and was not PAV-aged because the ALF sections were trafficked at a relatively early age. Strain levels between 3 and 9 percent are relatively large and not within the linear viscoelastic range that was estimated to represent the magnitude of strain likely to be encountered at the micromechanical level. The point of failure was defined as when the modulus decreased to 50 percent of the initial (undamaged) modulus. The data indicated some strain sensitivity of fatigue ranking. The ranking of the unmodified binders does not change: air blown performs better than the PG70-22 binder. The CR-TB binder exhibits better performance than terpolymer at the 3 percent strain level, but terpolymer is better at larger strain levels. Also, SBS-LG exhibits superior performance above all binders at all strain levels.
|
Binder |
Percent Strain |
Beginning of Test |
Conditions at Failure |
Number of Cycles to Failure, NF |
||
|---|---|---|---|---|---|---|
|
|G*| (MPa) |
Phase Angle (degrees) |
|G*| (MPa) |
Phase Angle (degrees) |
|||
|
PG70-22 |
3 |
23.11 |
45.46 |
12.73 |
46.97 |
49.63 |
|
5 |
18.16 |
50.28 |
9.35 |
51.51 |
11.77 |
|
|
7 |
15.54 |
53.67 |
7.65 |
54.68 |
4.64 |
|
|
Air blown |
3 |
12.71 |
44.99 |
6.48 |
46.75 |
108.97 |
|
5 |
10.57 |
49.06 |
5.46 |
51.1 |
26.02 |
|
|
7 |
9.36 |
51.94 |
4.87 |
54.18 |
10.12 |
|
|
SBS LG |
5 |
6.05 |
49.41 |
3.02 |
57.05 |
1167.1 |
|
7 |
4.99 |
52.5 |
2.5 |
58.58 |
236.48 |
|
|
9 |
4.32 |
54.95 |
2.16 |
59.76 |
71.16 |
|
|
CR-TB |
3 |
5.35 |
54.21 |
2.85 |
55.45 |
845.43 |
|
5 |
4.37 |
57 |
2.24 |
58.03 |
51.73 |
|
|
7 |
3.66 |
59.1 |
2.11 |
60.13 |
12.63 |
|
|
Terpolymer |
3 |
6.25 |
50.5 |
3.29 |
53.62 |
532.63 |
|
5 |
5.82 |
52.74 |
3.47 |
55.74 |
158.67 |
|
|
7 |
5.17 |
55.46 |
3.16 |
57.79 |
45.68 |
|
1 MPa = 145 psi
The stress sweeps conducted by Martono and Bahia were also conducted at 66 °F (19 °C) and 10 Hz.(65) The imposed stress increased from 0.145 to 290 psi (1 to 2,000 kPa) in 8 percent increments. Failure was defined as the point where the maximum value calculated by the parameter in figure 109 was reached. Results are shown in table 65.
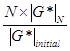
Figure 109. Equation. Stress sweep parameter.
|
Binder |
Beginning of Test |
Point of Failure |
|||||
|---|---|---|---|---|---|---|---|
|
|G*| (MPa) |
Phase Angle (degrees) |
Stress |
Strain |
|G*| (MPa) |
Phase Angle (degrees) |
Number of Cycles to Failure, NF |
|
|
Terpolymer |
6.92 |
47.3 |
0.33 |
10.14 |
3.46 |
58.87 |
6.35 |
|
CR-TB |
5.02 |
52.07 |
0.39 |
16.5 |
2.51 |
63.1 |
6.49 |
|
SBS LG |
8.9 |
40.64 |
0.39 |
9.17 |
4.45 |
54.15 |
6.5 |
|
Air blown |
15.22 |
41.65 |
0.68 |
9.11 |
7.64 |
54.2 |
7.09 |
|
PG70-22 |
25.3 |
41.41 |
1.05 |
8.5 |
12.65 |
55.63 |
7.57 |
1 MPa = 145 psi
Shenoy proposed the use of a strain sweep test in order to establish an intermediate-temperature specification parameter.(66) The procedure relied exclusively on the generation of strain sweep data on RTFO-aged binders. The following procedure was used for determining the intermediate-temperature specification parameter:(66)
1. Using a frequency of oscillations of 10 radians/s, strain sweeps were run at three of four temperatures chosen from 50, 66, 77, and 82 °F (10, 19, 25, and 28 °C), depending on the stiffness level of the binder. For softer binders, 50, 66, and 77 °F (10, 19, and 25 °C) were used, and for stiffer binders, 66, 77, and 82 °F (19, 25, and 28 °C) were used. For all ALF binders in the study, 66, 77, and 82 °F (19, 25, and 28 °C) were used. The percent strains were chosen from 0.01 to 100 percent, with 10 points per decade with log increase. The sampling time was 3 s for one data point per strain level.
2. The values of the complex modulus |G*| at the strain level of 25 percent at each of the three temperatures were used in order to calculate the temperature Te (°C) at which the complex modulus |G*s| would have a value of 145 psi (1 MPa), as shown figure 110.
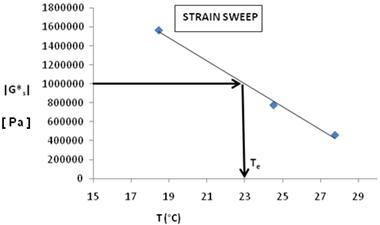
1 Pa = 0.000145 psi
°F = 1.8(°C) + 32
Figure 110. Graph. Complex shear modulus and temperature during 25 percent controlled strain test.
3. The values of the loss modulus G''s = |G*|sinδs at the strain level of 25 percent at each of the three temperatures were used in order to calculate the value of the loss modulus G''s at the temperature Te (°C), as shown in figure 111.
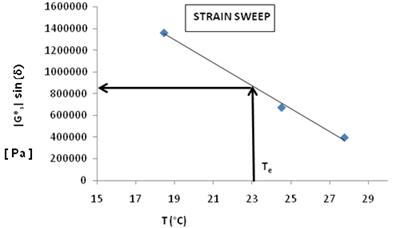
1 Pa = 0.000145 psi
°F = 1.8(°C) + 32
Figure 111. Graph. Loss modulus and temperature during 25 percent controlled strain test.
4. The intermediate-temperature specification TIS was then calculated as Te (G''s /|G*s|) or
Te sinδsand was used for ranking the binders in terms of their expected fatigue performance.
Test results on the ALF binders are provided in table 66.
|
Binder |
|G*|sin 19 °C, 10 radians/s, |
TEsin |
|---|---|---|
|
PG70-22 |
3,940,000 |
28.1 |
|
Air blown |
2,390,000 |
24.8 |
|
CR-TB |
1,280,000 |
19.1 |
|
SBS-LG |
1,360,000 |
19.2 |
|
Terpolymer |
910,000 |
16.8 |
|
SBS 64-40 |
489,000 |
11.3 |
1 Pa = 0.000145 psi
°F = 1.8(°C) + 32
Queen’s University researchers proposed evaluation of the energy needed for fracturing ductile materials to get a measure of the fatigue and crack resistance behavior of asphalt binders.(67) The essential work of fracture (EWF) approach has a history of application in the failure characterization of ductile materials such as plastics, certain metals, and composite materials.(68–70) Prior to the development of the EWF method, the fracture resistance of viscoplastic materials was largely evaluated by using laborious techniques requiring explicit measurements of a crack advancing through material. There had been many attempts to evaluate the work required to create new surfaces in intact material (i.e., cracking). The work necessary to pull apart a prenotched elastoplastic specimen is assumed to be divided in two parts: essential work performed in the local region of the advancing crack creating two surfaces and non-essential work away from the local region of cracking/tearing associated with ductility, plasticity, and yielding.(69)
The experimental determination of the essential and non-essential work of fracture involves the following steps. First, total work of fracture is determined in simple DT tests of similar specimens with different ligament lengths. Double edged notched tension (DENT) samples were used in the characterization of ALF following a protocol developed in Ontario Ministry of Transportation Test Method LS-299.(71) Figure 112 is a schematic of the sample in the DENT test defining ligament length, and figure 113 shows the test samples in a computer-controlled force-ductility instrument. Figure 114 provides an example of raw force versus displacement data after a DENT test using three ligament lengths and two replicates for each ligament. The ALF binders were PAV-aged instead of only RTFO-aged. The test temperature was 77 °F (25 °C), and the extension rate was 4 inches/min (100 mm/min). Ligament lengths were 0.2, 0.4, and 0.58 inches (5, 10, and 15 mm). The areas underneath the force versus displacement curves in figure 114 represent the total work of fracture. These values divided by the sectional area of each corresponding ligament (0.2, 0.4, and 0.58 inches (5, 10, and 15 mm) multiplied by 0.25 inches (6.5 mm) representing the sample thickness) represent the total specific work of fracture. Second, the values of the specific fracture energies are plotted on a graph versus the ligament lengths. A straight line results when total specific work of fracture, Wf, is plotted against ligament length, as shown in figure 115.
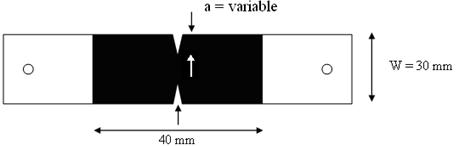
1 mm = 0.039 inches
Figure 112. Illustration. Plan view drawing of DENT test specimen design.

Figure 113. Photo. DENT test specimens loaded in ductilometer.
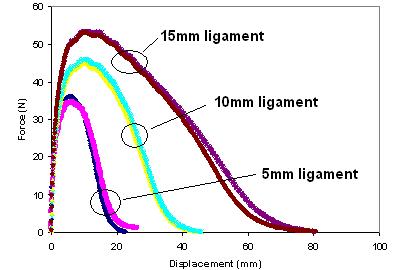
1 N = 0.225 lbf
1 mm = 0.039 inches
Figure 114. Graph. Typical raw data from DENT test.
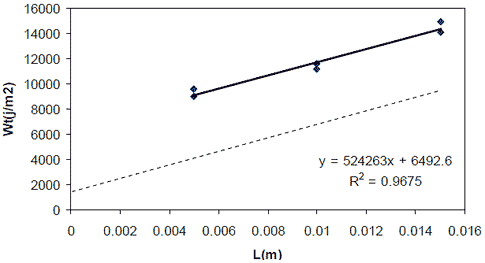
1 J/m2 = 0.0685 lb-ft/ft2
1 m = 3.28 ft
Figure 115. Graph. Total work of fracture versus ligament length.
Some background on the mathematics is provided for clarity. The EWF, We, is proportional to the fracture area (i.e., ligament length, l, multiplied by thickness, B), while the non-essential or plastic work, Wp, is proportional to the volume of the plastic zone. This is fracture area (l ×
B) multiplied by ligament length, multiplied with factor ![]() . The
. The ![]() factor depends on the shape of the plastic zone. Because the ligament length has major importance in determining the extent of plastic deformation, it is distinctly incorporated as l ×
factor depends on the shape of the plastic zone. Because the ligament length has major importance in determining the extent of plastic deformation, it is distinctly incorporated as l ×
![]() and multiplied with the surface area to express the volume dependence of the plastic work of fracture, Wp. The rather simple mathematical expression for the total work of fracture, Wf, is as shown in figure 116.
and multiplied with the surface area to express the volume dependence of the plastic work of fracture, Wp. The rather simple mathematical expression for the total work of fracture, Wf, is as shown in figure 116.
![]()
Figure 116. Equation. Total work of fracture.
Where:
Wf= Total work of fracture.
We = EWF.
Wp = Total plastic work of fracture.
l = Ligament length.
B = Thickness.
we = Specific essential work of fracture .
wp = Specific work of fracture.
The ![]() parameter is determined considering the degree to which the sample geometry follows plane-strain or plane-stress conditions. In this scenario,
parameter is determined considering the degree to which the sample geometry follows plane-strain or plane-stress conditions. In this scenario, ![]() is calculated as shown in figure 117.
is calculated as shown in figure 117.
![]()
Figure 117. Equation. DENT beta parameter.
Where:
h = Height of an assumed elliptic shape of the plastic zone.
L = Ligament length.
Using a linear fitting procedure similar to the one employed for the EWF analysis, the calculated critical tip opening displacement (CTOD), ![]() , is the ultimate elongation for a zero ligament length, which represents the strain tolerance in the vicinity of a crack. In this study, the tensile yield stress was approximated with the net section stress (peak load divided by the sectional area) for the smallest ligament length (0.2 inches (5 mm)). This allowed an approximate CTOD to be calculated from the ratio between the essential work and the net section stress, as shown in figure 118.
, is the ultimate elongation for a zero ligament length, which represents the strain tolerance in the vicinity of a crack. In this study, the tensile yield stress was approximated with the net section stress (peak load divided by the sectional area) for the smallest ligament length (0.2 inches (5 mm)). This allowed an approximate CTOD to be calculated from the ratio between the essential work and the net section stress, as shown in figure 118.
![]()
Figure 118. Equation. Approximate CTOD.
EWF and CTOD test results on the ALF binders are provided in table 67 along with the yield stress at the smallest ligament length (0.2 inches (5 mm)). The polymer modified binders have the largest CTOD, and the unmodified binders have the lowest. There is a general trend of rank in EWF, but this is not the case for the yield stress. The EWF and CTOD testing methodologies were carried out on mixtures under different conditions, as discussed in the next chapter. Furthermore, the results from an Ontario Ministry of Transportation field test will be discussed in light of the statistical comparison methodologies in chapter 7.
|
Binder |
EWF |
Yield Stress (kPa) |
Calculated CTOD (mm) |
|---|---|---|---|
|
SBS 64-40 |
4.4 |
102 |
43.1 |
|
CR-AZ |
10.6 |
249 |
42.6 |
|
SBS-LG |
1.02 |
43 |
24.0 |
|
Terpolymer |
0.85 |
54 |
15.7 |
|
CR-TB |
0.60 |
71 |
8.5 |
|
PG70-22 |
0.97 |
129 |
7.5 |
|
Air blown |
0.70 |
103 |
6.8 |
1 kJ = 23,730 lb-ft2/s2
1 kPa = 0.145 psi
1 mm = 0.039 inches
Johnson et al. suggested the use of the yield energy to identify the relative performance of asphalt binders.(72) The method involves the evaluation of the amount of energy to cause yielding in the asphalt binder. PAV-aged binder is tested in the DSR using the 0.3-inch (8-mm) parallel plate with a 0.08-inch (2-mm) gap. The sample is subjected to monotonic shear using a constant shear rate until peak strength is achieved and the sample yields. At the temperature of interest, a constant shear rate of 1 percent strain per second is used, and the test is continued until the material achieves 3,600 percent strain in 60 min. The shear stress and the shear strain percent are recorded at a sampling rate of one data point every 2 s. A typical plot of the shear stress versus shear strain is shown in figure 119. The ranked results are shown in table 68.
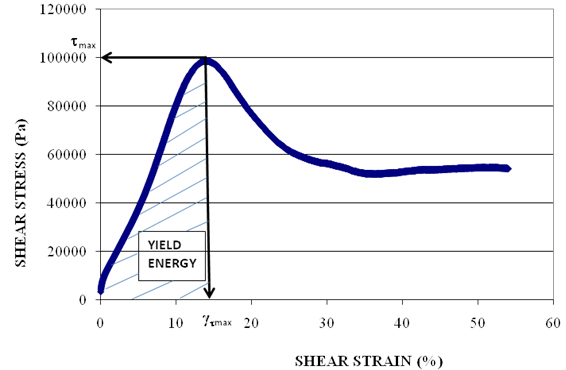
1 Pa = 0.000145 psi
Figure 119. Graph. Typical raw data measured during monotonic binder strength test for yield energy.
|
Binder |
Yield Energy, RTFO-Aged, |
|---|---|
|
Terpolymer* |
2.393 |
|
SBS-LG* |
1.921 |
|
CR-TB* |
1.759 |
|
PG70-22* |
0.342 |
|
Air blown* |
0.231 |
|
SBS 64-40** |
0.0157 |
1 MPa = 145 psi
*Reported by Johnson et al.(72)
**Tested at FHWA’s TFHRC.
As described in chapter 3, the rutting performance of the ALF lanes was not very diverse. Although there were quantifiable differences in the mean rutting, the variability reduced the significance of those differences to a point where many lanes were statistically equivalent despite different asphalt binders. This challenges the development of meaningful relationships and comparisons between binder properties. For completeness and clarity, descriptions and test results from high-temperature binder candidate specification tests are detailed in this report, including the MSCR method, which was recently implemented in AASHTO TP 70 and table 3 of AASHTO M 320, Standard Specification for Performance-Graded Asphalt Binder.(73,2)
ALF binder test results from the standard specification test (AASHTO T 315) using the DSR to control rutting at the high temperature range are provided in table 69.(5) Both the specification temperature and the stiffness at the fixed ALF loading temperature of 147 °F (64 °C) are provided. In addition, an alternative set of criteria with a frequency of oscillation at 0.25 radians/s rather than 10 radians/s and a stiffness of 0.0073 psi (50 Pa) instead of 0.31 psi (2.2 kPa) is provided to focus on softer ends of the stiffness spectrum and highlight binder modification benefits. The ranking is a bit different from parameters where the modified and unmodified binders are intermingled, and the ranking is different depending on the frequency of oscillation.
|
Binder |
|G*|/sinδ value 64 °C, 10 radians/s |
Temperature at |G*|/sinδ = 2.2 kPa, 10 radians/s (°C) |
|G*|/sinδ value 64 °C, 0.25 radians/s |
Temperature at |
|---|---|---|---|---|
|
CR-AZ |
— |
86.4 |
— |
— |
|
CR-TB |
12,846 |
82.2 |
952 |
89.8 |
|
Air blown |
10,851 |
76.9 |
412 |
79.2 |
|
PG70-22 |
6,903 |
73.6 |
233 |
75.5 |
|
SBS-LG |
6,321 |
74.7 |
367 |
80.8 |
|
Terpolymer |
5,359 |
74.6 |
388 |
85.6 |
|
SBS 64-40 |
5,192 |
73.9 |
454 |
84.6 |
1 Pa = 0.000145 psi
°F = 1.8(°C) + 32
— Indicates data were not collected.
D’Angelo and Dongré extended the NCHRP 9-10 binder creep and recovery characterization approach and suggested a further refined high-temperature binder specification through the use of an MSCR test.(20,74,75) The idea behind the approach suggested by D’Angelo and Dongré is to get the nonrecovered compliance as a measure for the high-temperature specification as it relates to the binder contributions in the roadway permanent deformation.(75) The test introduces stress sensitivity and a recoverable strain response along with the nonrecoverable response, that is, an alternative to elastic recovery specifications (ASTM D5976, AASHTO T 51).(76,77)
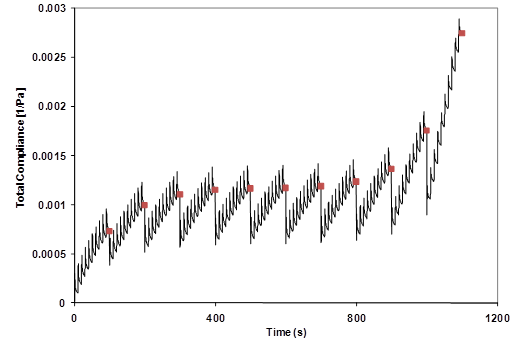
Before being refined and adopted by AASHTO, early versions of the protocol consisted of applying creep loads beginning with 0.0036 psi (0.025 kPa) for a 1-s duration followed by a 9-s recovery period for 10 cycles in the DSR. This was followed with doubling the creep load to 0.0073 psi (0.050 kPa) for a 1-s duration followed by a 9-s recovery period for 10 cycles, and continuing by doubling the load each time until 0.46 psi (3.2 kPa) and until much a higher load of 3.71 psi (25.6 kPa).(74,75) This process is shown graphically in figure 120 in semilog scale. Figure 121 and figure 122 illustrate how the strain grows with each cycle then recovers with some irrecoverable portion before the next cycle of stress is applied. The accumulated strain after each creep and recovery cycle for the 10 cycles is divided by the imposed stress (![]() 0) to produce compliance, as shown in figure 123. The nonrecovered compliance at the end of each group of stresses is then determined, as shown in filled circles in figure 123.
0) to produce compliance, as shown in figure 123. The nonrecovered compliance at the end of each group of stresses is then determined, as shown in filled circles in figure 123.
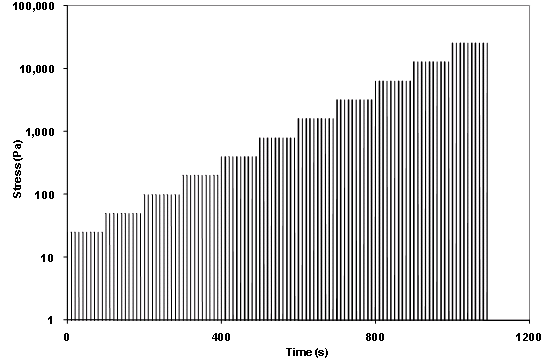
1 Pa = 0.000145 psi
Figure 120. Graph. Typical applied binder shear stresses during MSCR test.
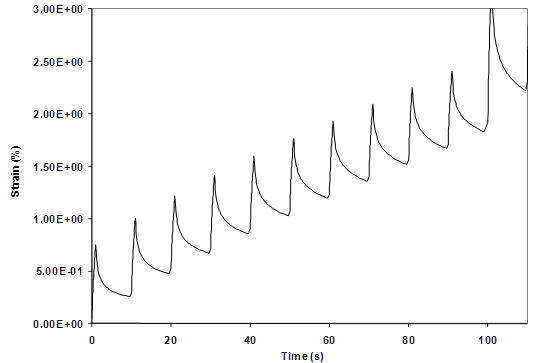
Figure 121. Graph. Measured raw strain data during MSCR test.
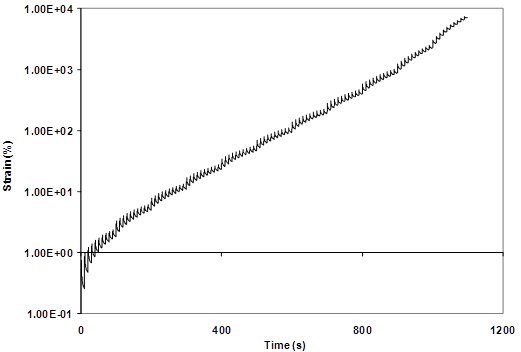
Figure 122. Graph. Measured raw strain data during entire MSCR test.
1 Pa = 0.000145 psi
Figure 123. Graph. Creep compliance variation during MSCR test where strain is normalized by applied stress.
The results for the ALF binders are provided in table 70 for creep stress levels of 0.0072, 0.058, and 0.46 psi (50, 400, and 3,200 Pa), although other stresses between and above these values were used in the test. Overall, the ranking of the materials’ response is the same for these stress levels. The polymer modified asphalts have the best performance, and the unmodified binders have the worst.
|
Binder |
Nonrecovered Compliance (1/MPa) |
||
|---|---|---|---|
|
50 Pa |
400 Pa |
3,200 Pa |
|
|
SBS 64-40 |
0.93 |
1.07 |
1.17 |
|
CR-TB |
1.12 |
1.20 |
1.40 |
|
SBS-LG |
1.65 |
1.76 |
2.33 |
|
Terpolymer |
2.99 |
3.40 |
3.98 |
|
Air blown |
4.99 |
5.73 |
6.38 |
|
PG70-22 |
9.47 |
11.30 |
12.33 |
1 Pa = 0.000145 psi
In 2001, Shenoy began developing a parameter |G*|/(1–(1/tanδsinδ)) that essentially provides the same measured nonrecoverable response as MSCR, since the parameter itself is, by definition, the inverse of the nonrecovered compliance. (See references 78–81.) The high specification temperature THS (°C) has been specified by Shenoy as the temperature at which the term |G*|/(1–(1/tandsind)) takes a value of 0.007 psi (50 Pa) for RTFO-aged binders at
![]() = 0.25 radians/s.(79) This is in contrast to the Superpave® high-temperature specification that is taken at a somewhat stiffer condition, faster frequency, and greater sensitivity to phase angle than sinδ.
= 0.25 radians/s.(79) This is in contrast to the Superpave® high-temperature specification that is taken at a somewhat stiffer condition, faster frequency, and greater sensitivity to phase angle than sinδ.
Shenoy showed that the unrecovered strain in a binder that is periodically subjected to an applied stress could be estimated directly from the DSR frequency sweep test data.(78) An expression for percent unrecovered strain was derived by Shenoy, as shown in figure 124.(78)
![]()
Figure 124. Equation. Derived estimate of percent unrecovered strain.
To minimize the unrecovered (or permanent) strain, the equation in figure 125, the inverse of the nonrecovered compliance, Percent![]() unr/100
unr/100 ![]() 0, needs to be maximized.
0, needs to be maximized.
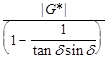
Figure 125. Equation. Derived estimate of unrecovered compliance.
The Shenoy parameter |G*|/(1–(1/tanδsinδ)) was thus suggested as a refinement to the Superpave® specification parameter for performance grading of asphalts.(78) This parameter is more sensitive to changes in δ than the parameter |G*|/sinδ. This is an important requirement conceptually because the refined parameter is sought for capturing the rutting behavior of polymer modified asphalts that are known to exhibit enhanced elasticity, which is illustrated in figure 126, comparing the behavior against the standard Superpave® high-temperature parameter. The two highlighted data points represent the values at 147 °F (64 °C), where there is less separation between the two binders than with the oscillatory-based nonrecovered compliance parameters shown in figure 127.
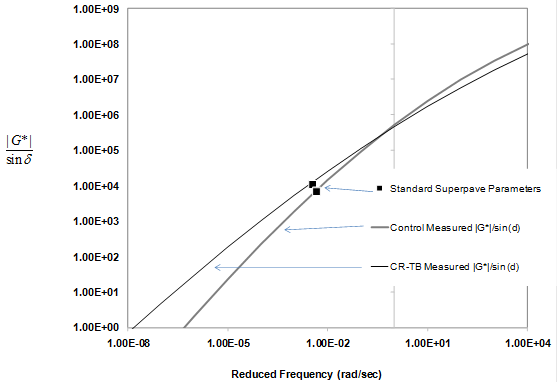
Figure 126. Graph. Standard high-temperature Superpave® rutting parameter in log scale versus reduced frequency in log scale.
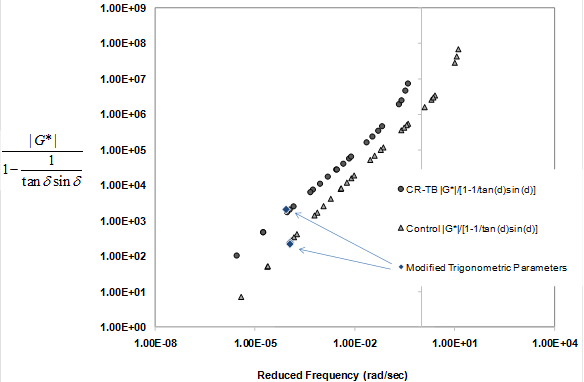
Figure 127. Graph. Oscillatory-based nonrecovered compliance rutting parameter in log scale versus reduced frequency in log scale.
It was shown during the derivation of the Shenoy parameter |G*|/(1–(1/tanδsinδ)) that the term (1 ‒ (1/tanδsinδ)) tends to be zero at δ equal to about 52 degrees.(78) Hence, the parameter is rendered invalid at values of δ less than 52 degrees. During the course of the development of this parameter and the further development of the new criterion, when a host of binders were considered, it was found that δ less than 52 degrees was encountered in less than 1 percent of the total number of data points analyzed.(78,79) Since the |G*|/(1 ‒ (1/tanδsinδ)) value is picked up at![]() = 0.25 radians/s, it is virtually impossible (or rather the chances are very remote) to encounter δ less than 52 degrees. Even so, if one has to safeguard against any adverse situation and be prepared for the 0.1 percent chance, then one can use the fact that |G*|/(sinδ)9 (i.e., sinδraised to the ninth power) is a close enough approximation, as proven earlier.(78) The parameter |G*|/(sinδ)9 can thus be used for δ less than 52 degrees. An if/then clause for the calculation using the formula "IF (δ>55, |G*|/(1 – (1/tanδsinδ)), |G*|/(sind)9)" in the Microsoft Excel® column does the job. Note that the cutoff value is taken to be 55 rather than 52 to be conservative. Using |G*|/(sinδ)9 as the refined parameter for all values of δ instead of |G*|/(1–(1/tanδsinδ)) is not appropriate because |G*|/(sinδ)9 does not have any fundamental basis, while the parameter |G*|/(1 – (1/tanδsinδ)) was derived using fundamental considerations. Figure 128 illustrates how a temperature grade in degrees Celsius can be determined using the Shenoy parameter with a recommended criterion of 0.0073 psi (50 Pa) in the same fashion as a temperature grade is determined with the current |G*|/sinδ parameter.
= 0.25 radians/s, it is virtually impossible (or rather the chances are very remote) to encounter δ less than 52 degrees. Even so, if one has to safeguard against any adverse situation and be prepared for the 0.1 percent chance, then one can use the fact that |G*|/(sinδ)9 (i.e., sinδraised to the ninth power) is a close enough approximation, as proven earlier.(78) The parameter |G*|/(sinδ)9 can thus be used for δ less than 52 degrees. An if/then clause for the calculation using the formula "IF (δ>55, |G*|/(1 – (1/tanδsinδ)), |G*|/(sind)9)" in the Microsoft Excel® column does the job. Note that the cutoff value is taken to be 55 rather than 52 to be conservative. Using |G*|/(sinδ)9 as the refined parameter for all values of δ instead of |G*|/(1–(1/tanδsinδ)) is not appropriate because |G*|/(sinδ)9 does not have any fundamental basis, while the parameter |G*|/(1 – (1/tanδsinδ)) was derived using fundamental considerations. Figure 128 illustrates how a temperature grade in degrees Celsius can be determined using the Shenoy parameter with a recommended criterion of 0.0073 psi (50 Pa) in the same fashion as a temperature grade is determined with the current |G*|/sinδ parameter.
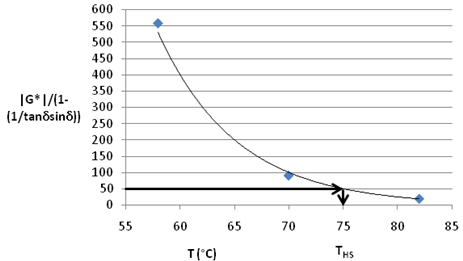
°F = 1.8(°C) + 32
Figure 128. Graph. Oscillatory-based nonrecovered compliance rutting parameter in arithmetic scale versus temperature in log scale.
An alternative criterion was also suggested by Shenoy.(79,80) First an equi-stiffness temperature TE (°C) was defined as the temperature when |G*| takes a value of 0.0073 psi (50 Pa) for the RTFO-aged binder at ![]() = 0.25 radians/s, thereby taking care of the rheological contribution coming from one portion of the term |G*|/(1–(1/tanδsinδ)). The contribution from the other portion was incorporated by dividing the equi-stiffness temperature TE (°C) by (1 – (1/tanδsinδ)) using δ values at TE (°C). This resulted in the high specification temperature THS (°C) being defined as TE/(1 – (1/tanδsinδ)). The sensitivity of the term 1/(1 – (1/tanδsinδ)) compared to 1/sinδ is shown in figure 129. The increased sensitivity of the term 1/(1 – (1/tanδsinδ)) to δ helps capture the elastic contribution of the modified asphalts in an enhanced manner compared to the term 1/sinδ.
= 0.25 radians/s, thereby taking care of the rheological contribution coming from one portion of the term |G*|/(1–(1/tanδsinδ)). The contribution from the other portion was incorporated by dividing the equi-stiffness temperature TE (°C) by (1 – (1/tanδsinδ)) using δ values at TE (°C). This resulted in the high specification temperature THS (°C) being defined as TE/(1 – (1/tanδsinδ)). The sensitivity of the term 1/(1 – (1/tanδsinδ)) compared to 1/sinδ is shown in figure 129. The increased sensitivity of the term 1/(1 – (1/tanδsinδ)) to δ helps capture the elastic contribution of the modified asphalts in an enhanced manner compared to the term 1/sinδ.
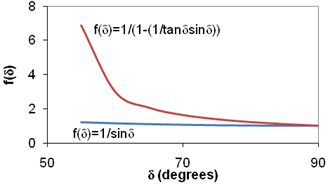
Figure 129. Graph. Trigonometric functions for the standard high-temperature Superpave® rutting parameters and oscillatory-based non-recovered compliance.
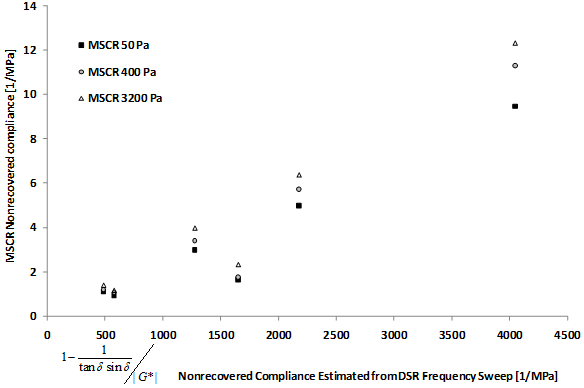
The ranked ALF binder properties from this technique are provided in table 71 for both the stiffness at the fixed temperature of 147 °F (64 °C) and the effective temperature. As previously described, the inverse of the modified trigonometric parameters is an estimate of the nonrecovered compliance derived from the theory. Figure 130 shows nonrecovered compliance from MSCR measurement with the nonrecovered compliance from the frequency sweep measurement. Although the two parameters are not numerically identical, they exhibit a very strong relationship.
|
Binder |
|G*|/(1-(1/tan |
TE/ (1–(1/tan |
|---|---|---|
|
CR-TB |
2,053 |
89.0 |
|
SBS 64-40 |
1,729 |
83.8 |
|
Terpolymer |
783 |
86.8 |
|
SBS-LG |
605 |
81.2 |
|
Air blown |
459 |
79.4 |
|
PG70-22 |
247 |
75.6 |
°F = 1.8(°C) + 32
1 Pa = 0.000145 psi
1 MPa = 145 psi
Figure 130. Graph. Measured nonrecovered compliance from MSCR test versus nonrecovered compliance estimated from shear modulus and phase angle from DSR frequency sweep.
Rowe et al. suggested the use of the ZSV ![]() 0 as the high-temperature specification parameter.(82) ZSV, by definition, is the viscosity at which there is no deformation. The method involves the determination of the relaxation spectra and using the asymptote to estimate the ZSV. ZSV or steady-state viscosity was defined as the loss modulus divided by the frequency as frequency approaches zero, as shown in figure 131 and figure 132.
0 as the high-temperature specification parameter.(82) ZSV, by definition, is the viscosity at which there is no deformation. The method involves the determination of the relaxation spectra and using the asymptote to estimate the ZSV. ZSV or steady-state viscosity was defined as the loss modulus divided by the frequency as frequency approaches zero, as shown in figure 131 and figure 132.
![]()
Figure 131. Equation. ZSV.
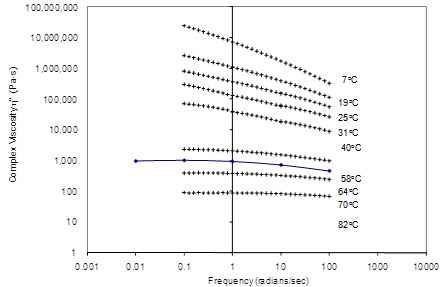
Figure 132. Graph. Complex viscosity in log scale versus frequency in log scale.
In the case of unmodified binder, a plateau develops when a master curve of dynamic viscosity versus reduced frequency is plotted, and ZSV is well defined by the asymptote. In the case of modified binders, no such plateau develops, as shown in figure 133, which compares the behavior measured from the unmodified PG70-22 binder and the modified CR-TB binder. When ZSV cannot be determined using the asymptote, RHEA ZSV™ software helps obtain a good approximation of ZSV.
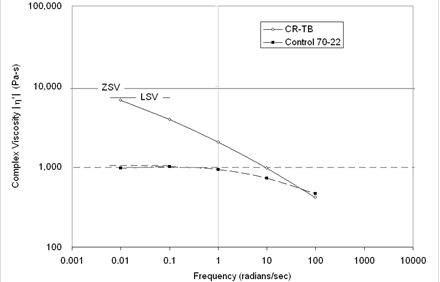
Figure 133. Graph. Complex viscosity in log scale versus frequency in log scale.
Dongré et al. suggested the use of low shear viscosity (LSV) at a fixed frequency of 0.01 radians/s as the high-temperature specification parameter, as shown in figure 133 for the unmodified binder.(83,84) This parameter could be obtained directly from the experiment and did not need separate software for calculation as in the case of ZSV. The ZSV and LSV test results on the ALF binders are provided in table 72.
|
Binder |
ZSV (Pa-s) |
LSV (Pa-s) |
|---|---|---|
|
CR-TB |
9,302 |
7,183 |
|
SBS 64-40 |
7,791 |
7,660 |
|
SBS-LG |
4,814 |
3,364 |
|
Terpolymer |
2,974 |
2,470 |
|
Air blown |
1,981 |
2,455 |
|
PG70-22 |
978 |
1,034 |
As a quick and easy method, Shenoy suggested the possibility of using the material’s volumetric-flow rate (MVR) as a high-temperature PG specification.(85,86) MVR is defined as the volume of the material (in milliliters or cubic centimeters) that is extruded in 10 min through a die of specific diameter and length by applying pressure through static weight load (L) under prescribed temperature conditions.
The MVR is determined through a closely defined flow measurement device (FMD) (see figure 134). This equipment is borrowed from the polymer industry, where it is routinely used to measure the melt flow index of polymers for purposes such as determining the suitability of polymer for blow injection molding. The equipment is less costly than by about a factor of 10 compared to dynamic shear rheometers. The cylinder of the FMD is made of hardened steel and is fitted with heaters, insulated, and controlled for operation at the required temperature. The heating device is capable of maintaining the temperature at 0.4 inches (10 mm) above the die to within 0.4 °F (0.2 °C) of the desired temperature during the test. The temperature of the barrel from 0.4 to 2.9 inches (10 to 75 mm) above the top of the die is maintained within ±1 percent of the set temperature (°C) in strict compliance with ASTM D1238.(87) The piston is made of steel, and the diameter of its head is 0.0029 ±0.00058 inches (0.075 ±0.015 mm) less than that of the internal diameter of the cylinder, which is 0.37 inches (9.5 mm). Extrusion of the material is done through a die made of hardened steel with an internal diameter of 0.0817 ±0.0002 inches (2.095 ±0.005 mm).
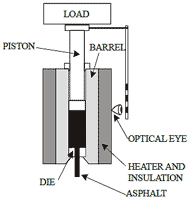
Figure 134. Illustration. Key components of an FMD for determination of MVR.
MVR can be effectively used in determining the PG high-temperature specification. The method is straightforward, fast, and accurate. The high specification temperature THS (°C) has been specified by Shenoy as the temperature at which MVR takes a value of 50 cc/10 min for unaged binders when the imposed load on the sample forced out of a capillary is 2.697 lb (1.225 kg), as shown in figure 135.(85)
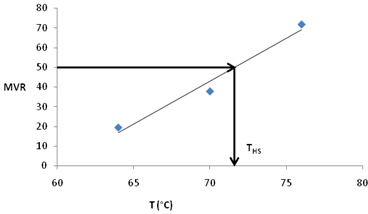
°F = 1.8(°C) + 32
Figure 135. Graph. MVR versus temperature.
MVR is easy to determine, and FMD that is used for the generation of MVR data is a relatively simple, inexpensive piece of equipment that can be carried from place to place because of its light weight. It neither needs arrangements for air pressure nor requires a circulating water bath to maintain a constant temperature environment. Since this equipment was originally built for taking polymer melt data at high temperatures (257–572 °F (125–300 °C)), it has an excellent temperature control system with variations of about 0.2 °F (0.1°C), especially in the temperature range applicable to paving asphalts. It was found that MVR data generated from the FMD were highly reproducible.
Because FMD is relatively inexpensive, the operational costs are low, the MVR data generation requires minimal training, the output has low level of variability, no calibration is needed, and the equipment is portable, it merits its use at paving sites or refineries. The actual time for data generation is also very low. All this makes MVR an attractive parameter to be used for routine quality control as well as for new product development of asphalt binders and would serve as an excellent purchase guide specification for the users and producers of paving asphalts.
MVR and corresponding temperature grading of the ALF binders is provided in table 73. The unmodified binders have a high flow rate, but the softest, SBS 64-40, has the highest rate. The other polymer modified binders have the lowest rates, with SBS-LG and CR-TB having the smallest.
|
Binder |
MVR at 64 °C, 1.225 kg |
Temperature at 50 cc/10 min, |
|---|---|---|
|
SBS-LG |
4.0 |
77.2 |
|
CR-TB |
4.4 |
80.6 |
|
Terpolymer |
6.1 |
81.2 |
|
PG70-22 |
11.7 |
73.5 |
|
Air blown |
14.6 |
74.8 |
|
SBS 64-40 |
19.1 |
77.0 |
°F = 1.8(°C) + 32
1 kg = 2.202 lb