Performance Testing for Superpave and Structural Validation

APPENDIX. DENT TEST METHOD SPECIFICATION

TITLE

The title of this document is "Standard Specification for Method of Test for the Determination of Asphalt Cement’s Resistance to Ductile Failure Using Double Edge Notched Tension Test (DENT)."

SCOPE

This test method covers the determination of asphalt cement’s resistance to ductile failure using a DENT test. The test is conducted after thermal conditioning to determine the EWF, the plastic work of fracture, and an approximate CTOD at a specified temperature and rate of loading. This method is provided as a provisional test method. The test is a working document; continuous refinement to the test method may be expected.

REFERENCED DOCUMENTS

The following documents are referenced in this specification:

• AASHTO R 28, Accelerated Aging of Asphalt Cement Using a Pressurized Aging Vessel (PAV).
• AASHTO T 240, Effect of Heat and Air on a Moving Film of Asphalt (Rolling Thin-Film Oven Test).
• AASHTO T 300, Force-Ductility Test of Bituminous Materials.
• AASHTO T 301, Elastic Recovery Test of Asphalt Materials by Means of a Ductilometer.
• AASHTO T 315, Determining the Rheological Properties of Asphalt Binder Using a Dynamic Shear Rheometer (DSR).
• ASTM D8, "Standard Definitions of Terms Relating to Materials for Roads and Pavements."
• ASTM D113, "Standard Test Method for Ductility of Bituminous Materials."
• MTO LS-299, Method of Test for Determining Asphalt Cement’s Resistance to Ductile Failure Using Double-Edge-Notched Tension Tests (Ministry of Transportation, Ontario).

TERMINOLOGY

The following terminology is used in this specification:

• W_t = Total work of fracture, area under the load versus load-line displacement curve, units J.
• w_t = Specific total work of fracture (W_t / Bℓ), units kJ/m².
• w_e = Specific EWF, the energy required to fracture or break the sample without plastic deformation away from the fracture zone, units kJ/m².
• w_p = Specific plastic work of fracture, the non-essential work dissipated during the deformation of a volume of asphalt around the fracture zone, units MJ/m³.
• β = Geometric constant describing the shape of the plastic zone.
• δ_t = CTOD, units mm.
• P = Load, units N.
• D = Displacement in test, units m.
• B = Sample thickness, units m.
• ℓ = Ligament length, the material between the notches, units m.
• σ_n = Net section stress of sample, units N/m².

APPARATUS

The following equipment is used in this specification:

• Mold: Consists of two end pieces and a pair of matching DENT inserts fitted together as shown in AASHTO T301.
• End pieces: Six end pieces from the elastic recovery specimen mold according to AASHTO T 301.
• DENT inserts: Six inserts made from type 360 brass, built to dimensions shown in figure 186. These inserts come in pairs, and each pair is manufactured to have a space between the matching pair of notches equal to the three different ligament lengths of 0.59, 0.39, and 0.2 inches (15, 10, and 5 mm) when fitted with the end pieces.

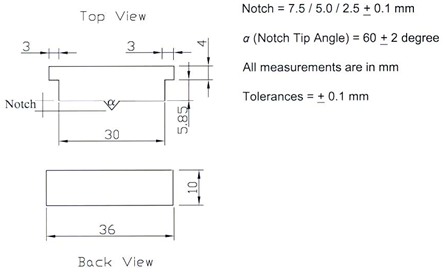
1 mm = 0.039 inches

Figure 186. Illustration. DENT inserts.

• Base plates: The base plates shall be made of non-absorbent material of sufficient thickness to prevent deformation and of a sufficient size to hold from one to three molds, but still able to fit in the temperature-controlled bath for conditioning. The plate shall be uniformly flat to ensure that the bottom surfaces of each mold will touch it throughout.
• Testing apparatus: A constant rate of displacement device capable of maintaining displacement at rates of 4 ±0.01 inches/min (100 ±2.5 mm/min). The maximum stroke for the instrument shall be 39.4 inches (1,000 mm) or greater. The apparatus should have a set of loading pins that ensure precise alignment of the sample during the test. The apparatus shall be able to determine displacement to an accuracy of 0.002 inches
  (±0.05 mm). (Note: DENT testing apparatus is commonly force-ductility apparatus installed in a ductilometer.)
• Load sensor: The sensitivity of the load sensor and recording electronics shall allow the load, P, to be measured every 0.3 s during the test with an accuracy of at least ±1 percent. The load sensor shall be capable of measuring a nominal maximum force of up to 29.9 lbf (133 N).
• Temperature-controlled bath for testing: The bath shall be large enough to contain the testing apparatus and samples in their molds prior to testing under a minimum of 1 inch (25 mm) of water. The equipment shall be capable of maintaining the water at the testing temperature to an accuracy of at least ±0.9 °F (±0.5 °C).
• Temperature-controlled bath for conditioning: The bath shall be capable of maintaining a minimum of 1 inch (25 mm) of water over the sample at the conditioning temperature requirements to within ±0.9 °F (±0.5 °C). Typically, the temperature-controlled bath for testing is utilized.
• Glass stir: Stick capable of stirring the hot asphalt cement vigorously.

PREPARATION OF SAMPLES

Prepare the DENT samples according to the Preparation of Apparatus and Molding of Test Specimens procedure in AASHTO T 300 with the following exceptions and additional requirements:

• Six samples shall be prepared using degassed PAV-aged asphalt cement, two for each ligament length of 0.59, 0.39, and 0.2 inches (15, 10, and 5 mm), by fitting each of the three matching pairs of inserts with three pairs of end pieces so the space between the matching pair of notches is equal to the three different ligament lengths to a tolerance of 0.001 inches (0.25 mm). Asphalt cement shall be aged according to AASHTO T 240 (RTFO) and AASHTO R 28 (PAV). The aged asphalt cement shall then be heated for 1 h at 320 ±9 °F(160 ±5 °C) to ensure that the asphalt cement readily flows when dispensed from the container into the prepared molds. (Note: The heating temperature may be raised to a maximum of 356 °F (180 °C) to provide a low enough viscosity, but the sample material should not be overheated.)
• Prior to pouring the asphalt cement into the mold, measure and record the actual ligament length, ℓ, to within 0.004 inches (0.1 mm).
• After any trimming, measure and record the sample thickness, B, in meters to four decimal places (to 0.1 mm). If trimmed flush with the mold, this will be the thickness of the mold.

TEST PROCEDURES

The following steps constitute the procedures for testing:

1.  Condition the samples on the base plates at 77 ±0.9 °F (25 ± 0.5 °C) for 3 h ±5 min in their molds in a temperature controlled bath under a minimum of 1 inch (25 mm) of water.

2.  Once conditioned, prepare the sample for testing by removing the sample from the base plate without causing excessive deformation or stress concentrations to the sample. Keep the sample always under the surface of the water, detach the DENT inserts, and load it through the holes in the end pieces onto the testing apparatus’ loading pins. The sample shall be loaded so there is a minimum of 1 inch (25 mm) of water below and above the sample. Allow the sample to sit and equilibrate for a minimum of 5 min before starting the test.

3.  Run the test according to AASHTO T 300 but at a displacement rate of 4 ±0.02 inches/min (100 ±2.5 mm/min) in a bath maintained at 77 ±0.9 °F (25 ± 0.5 °C) until ductile failure is reached or a stroke length of 39.4 inches (1,000 mm) is reached.

4.  If ductile failure is not achieved before the stroke length of 39.4 inches (1,000 mm) is reached, the test shall be stopped and retested at a lower displacement rate. Reheat the sample material in a manner that minimizes damage to the material (see Preparation of Sample section). Condition and retest according to steps 1–3 at a displacement rate of 2 ±0.01 inches/min (50 ±2.5 mm/min).

5.  Record actual sample ligament length, ℓ, displacement rate, water bath temperature, and load every 0.3 s for the entire test time.

6.  Repeat steps 1–5 on the duplicate and then on all the other ligament length samples.

CALCULATIONS

The following calculations should be performed following testing:

1.  Using numerical integration techniques, calculate the average W_t for each ligament length where W_tfor each sample is computed based on figure 187.

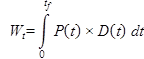
(units kJ)

Figure 187. Equation. Total work of fracture calculated from integration of load and displacement data.

Where t_f is the time when ductile failure or the maximum stroke length is reached, whichever comes first. (Note: Any negative load readings or negative W_t values and any W_t obtained after t_f are not to be included in the calculation. Although it is not always noticeable, additional data are often recorded for the run after failure. For example, when the load is very small and then increases slightly or the load is very small and remains constant, the data are a residual load on the device. Check each of the data records to ensure that these residual and any prestart values are zeroed so they are not included in the total W_t.)

2.  Calculate w_t for each ligament length for each average W_t where w_t is the (average W_t)/(Bℓ) (units J/m²).

3.  Plot w_t for the three ligamentlengths, ℓ and use the method of least squares to fit a regression line through the data. See figure 188 for an example.

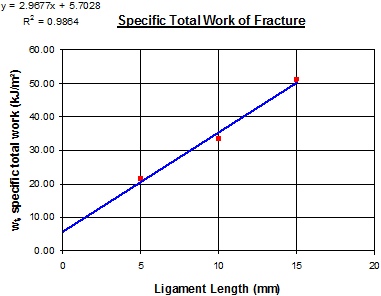
1 kJ = 23,730 lb-ft²/sec²
1 mm = 0.0309 inches

Figure 188. Graph. Example w_t versus ligament length plot for determining EWF.

Obtain values for w_e and the term , where w_e is the specific EWF (i.e., w_t for ℓ = 0.0) and is the slope of the best fit straight line, for . (Note: An individual value does not need to be calculated. As background for the user of this test, , where h is the height of an assumed elliptic shape of the plastic zone and L is the ligament length.)

4.  Determine , where = P_peak / (Bℓ) and P_peak is the average peak load obtained for the sample tested with the smallest ligament length (i.e., the average maximum load for the 0.2-inch (5-mm) ligament samples).

REPORTING RESULTS

Report the following on a form similar to figure 189: w_e, , , P_peak, best fit line for the w_t versus ligament lengths plot. For each ligament length, plot the average actual sample ligament length, the average actual sample thickness, average W_t, w_t, and load versus displacement curves, as in figure 190.

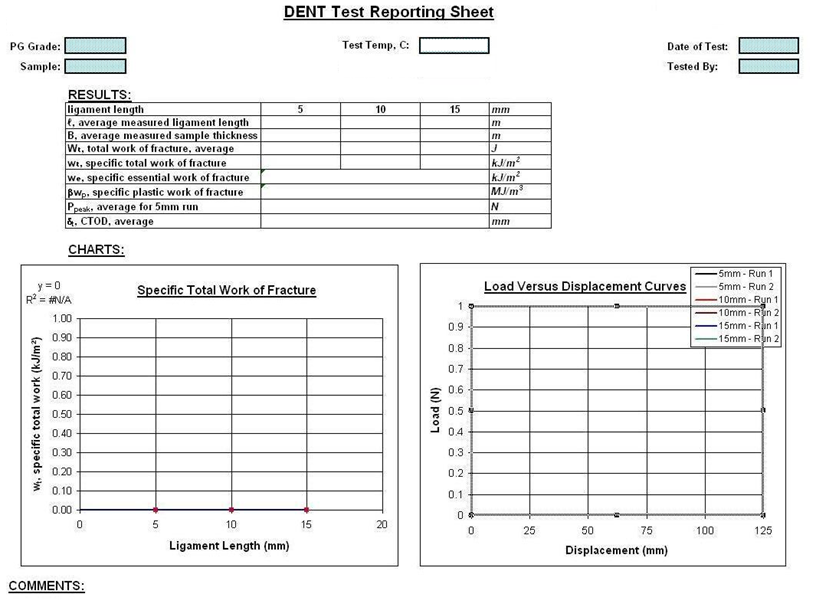
Figure 189. Chart. Example reporting sheet.

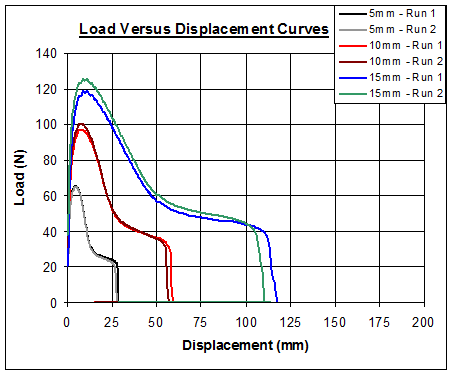
1 N = 0.225 lbf
1 mm = 0.0309 inches

Figure 190. Graph. Typical load-displacement curves for EWF test.