U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

 
REPORT
This report is an archived publication and may contain dated technical, contact, and link information
Back to Publication List        
Publication Number:  FHWA-HRT-13-090    Date:  April 2016
Publication Number: FHWA-HRT-13-090
Date: April 2016

 

MEPDG Traffic Loading Defaults Derived From Traffic Pooled Fund Study

CHAPTER 4-IMPORTANCE OF AXLE LOADS FOR PAVEMENT DESIGN USING THE MEPDG

PURPOSE OF INVESTIGATION

Understanding the sensitivity of MEPDG outputs to traffic loads is an important step in the development of procedures for computing axle loading inputs and defaults as well as axle loading data reliability procedures. The main reason is that the load level does not have a linear relationship with pavement performance-heavier loads have a greater impact on performance. Thus, accurate representation of heavier loads is more important than lighter load levels.

No universal damage factor is available that indicates how much more damaging heavy axles are in comparison to lighter axles in accordance with the MEPDG method. This is in part because the MEPDG method is complex, and the influence of traffic loads varies by site features, distresses, and pavement type. Nonetheless, the ability to quantify the relative importance of axle loads would be beneficial for comparing different axle load spectra.

In this study, the research team investigated the relative effect of different axle load levels on pavement performance using different pavement distress prediction models to develop RPPIFs (or importance factors), W, that would provide measure of relative importance of different axle loads for pavement design using MEPDG method.

RPPIF

A new parameter was developed for this study-RPPIF, or W factor. The intent of W factors is to provide a measure of the relative importance of one load level against another with regard to sensitivity of MEPDG outcomes to different loads. These factors are intended to be used as generalized weights of relative importance for different load magnitudes to aid in comparing different load spectra. They are not intended to be used in a direct correlation with a particular pavement deterioration model, as different pavement deterioration mechanisms and pavement design types are expected to have different sensitivities to various load levels.

To develop W factors, the research team conducted a series of MEPDG analyses by applying axle loads of different magnitudes-one axle load level and axle group type per MEPDG design scenario-to several typical pavement structures and evaluated the number of load applications of a given magnitude to cause the pavement structure to reach a terminal condition or failure in major load-associated distresses. Initially, the International Roughness Index (IRI) was considered as a pavement performance parameter, but it was dropped from further investigation as it became evident that IRI, in addition to load related distresses, was also affected by pavement material aging and environment.

The scope of MEPDG analysis was limited to eight flexible pavement scenarios and eight rigid pavement scenarios representing different classes of pavement structures located on road facilities with different functional use (rural interstates (RIs) and ROPA) and in different climatic zones. For flexible pavements, pavement design scenarios were developed based on a 15-year design life to achieve terminal values in one of the major distresses; a 20-year design period was used for rigid pavements. Design life values were selected based on average values observed for LTPP GPS sections. MEPDG default inputs, along with truck traffic classification (TTC) and average annual daily truck traffic (AADTT) levels typical for RI and ROPA roads were used to develop adequate pavement structures. Climatic conditions used in the MEPDG analyses included wet-freeze, wet-no freeze, dry-freeze, and dry-no freeze. Table 3 summarizes the pavement structures and climatic scenarios used in the sensitivity study.

Table 3. Pavement structures and climatic scenarios used in the sensitivity study.
Pavement and Climate Scenarios Highway Functional Class, AADTT, and TTC
Pavement Type Wet-Freeze Wet-No Freeze Dry-Freeze Dry-No Freeze
Flexible AC thickness:
6 inches		 AC thickness:
7 inches		 AC thickness:
7.8 inches		 AC thickness:
7 inches		 RI,
AADTT = 2,000, TTC 1
Base type/thickness: crushed stone/11-inch subbase base type/thickness: crushed stone/11-inch subbase base type/thickness: crushed stone/
11-inch subbase		 base type/thickness: crushed stone/
11-inch subbase
Type/thickness:
A-1-a/12 inches		 Type/thickness:
A-1-a/12 inches		 Type/thickness:
A-1-a, 12 inches 		Type/thickness:
A-1-a, 12 inches
Soil type: A-1-b Soil type: A-1-b Soil type: A-1-b Soil type: A-1-b
Flexible AC thickness:
4.2 inches		 AC thickness:
4 inches		 AC thickness:
5 inches		 AC thickness:
4 inches		 ROPA,AADTT = 500, TTC 6
Base type/thickness: crushed stone/
8 inches		 Base type/thickness: crushed stone/
8 inches		 Base type/thickness: crushed stone/
8 inches		 Base type/thickness: crushed stone/
8 inches
Soil type: A-1-b Soil type: A-1-b Soil type: A-1-b Soil type: A-1-b
Rigid PCC thickness:
10 inches		 PCC thickness:
11 inches		 PCC thickness:
11 inches		 PCC thickness:
11 inches		 RI,AADTT = 2,000, TTC 1
Dowel diameter/
spacing: 1.25 inches/
12 inches		 Dowel diameter/
spacing: 1.25 inches/
14 inches		 Dowel diameter/
spacing: 1.25 inches/
12 inches		 Dowel diameter/
spacing: 1.25 inches/
14 inches
Erodibility Index: 2 Erodibility Index: 2 Erodibility Index: 2 Erodibility Index: 2
Base type/
thickness: cement stabilized/6 inches		 Base type/
thickness: cement stabilized/6 inches		 Base type/
thickness: cement stabilized/6 inches		 Base type/
thickness: cement stabilized/6 inches
Subbase type/
thickness:
A-6/12 inches		 Subbase type/thickness:
A-6/12 inches		 Unknown Unknown
Soil type: A-6 Soil type: A-6 Soil type: A-6 Soil type: A-6
Rigid PCC thickness:
9 inches		 PCC thickness:
9 inches		 PCC thickness:
9 inches		 PCC thickness:
10 inches		 ROPA,AADTT = 700, TTC 2
Dowel diameter/
spacing: 1.25 inches/
12 inches		 Dowel diameter/
spacing: 1.25 inches/
14 inches		 Dowel diameter/
spacing: 1 inch/
10 inches		 Dowel diameter/
spacing: 1 inch/
12 inches
Erodibility index: 4 Erodibility index: 3 Erodibility index: 3 Erodibility index: 4
Base type/
thickness: soil cement/6 inches		 Base type/
thickness: A-6/
6 inches		 Base type/
thickness: cement stabilized/6 inches		 Base type/
thickness: soil cement/6 inches
Soil type: A-6 Soil type: A-6 Soil type: A-6 Soil type: A-6

AC = Asphalt concrete; PCC = Portland cement concrete.

In each MEPDG sensitivity run, one axle load level and axle group type was used to determine the number of load applications to failure in major load-associated distresses for a given pavement structure and climatic scenario. For flexible pavements, the following pavement performance parameters were considered: rutting and fatigue cracking or bottom-up alligator cracking. For rigid pavements, cracking and faulting were considered.

For each pavement type, climate zone, road type, axle group type, and load level, the number of load applications to failure was found for each pavement performance parameter from MEPDG runs, and the minimum number of loads to failure was determined among all pavement performance parameters at each load level. An example plot is shown in figure 5 for flexible and rigid pavements and for RI and ROPA design scenarios for the wet-freeze zone.

Figure 5. Graph. Example of MEPDG sensitivity results for different load levels. This graph shows an example of Mechanistic-Empirical Pavement Design Guide (MEPDG) sensitivity results for different load levels. The y-axis represents the number of axle applications to failure, and the x-axis represents the tandem axle load ranges in pounds. There are 12 series of points shown in the plot that correspond to distresses by functional class and pavement type. All 12 series of points resemble inverted J-shaped curves and show a steep decrease in the number of axle applications to failure with increase in tandem axle load ranges. There is a red vertical line representing the legal limit for tandem axles at 34,000 to 35,999 lb. Data points for the 12 series of points are represented as follows: blue triangular markers for flexible rural other principal arterial (ROPA) fatigue cracking, yellow triangular markers for flexible ROPA total cracking, continuous black line for flexible ROPA minimum, green square markers for flexible rural interstate (RI) fatigue cracking, burgundy square markers for flexible RI total cracking, continuous red line for flexible RI minimum, yellow diamond markers for rigid RI faulting, light purple diamond markers for rigid RI percent slabs cracked, dashed red line for rigid RI minimum, grey circular markers for rigid ROPA faulting, light blue circular markers for rigid ROPA percent slabs cracked, and dashed black line for rigid ROPA minimum. The maximum number of truck applications to failure for the various scenarios range from a little over 4.0E+07 to as high as 6.0E+07.

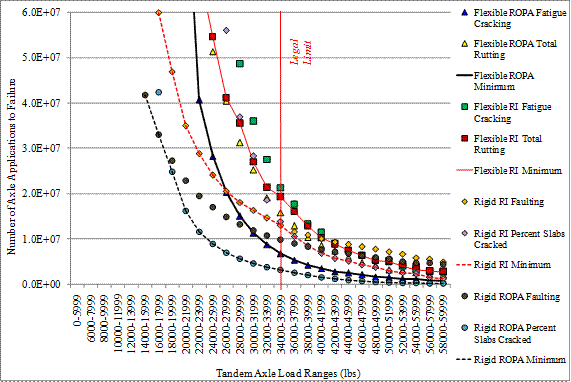
Figure 5. Graph. Example of MEPDG sensitivity results for different load levels.

For each pavement design scenario, the inverse of the minimum number of load application to failure was computed for each load level and normalized with respect to the inverse value computed at the legal load level (34,000 lb) for tandem axle loads. These values representW factors at individual load levels. Results of MEPDG analyses for each pavement design scenario were then used to compute single, tandem, tridem, and quad axle loads by averaging pavement performance impact factors, as shown in table 4. The decision to averageW factors over different pavement design types was based on the need to have a single set of W (importance) factors that would provide a means for evaluating the relative importance of different load levels and for comparing different axle load spectra, rather than to have a series of precise curves designed for different pavement scenarios or pavement types. Graphical representation of these factors is provided in figure 6.

Table 4. Pavement performance impact W factors.
Load Bin Single Tandem Tridem Quad
Load Range (lb) Weight Factor Load Range (lb) Weight Factor Load Range (lb) Weight Factor Load Range (lb) Weight Factor
BIN_01 0-999 0.00 0-1,999 0.00 0-2,999 0.00 0-2,999 0.00
BIN_02 1,000-1,999 0.00 2,000-3,999 0.00 3,000-5,999 0.00 3,000-5,999 0.00
BIN_03 2,000-2,999 0.00 4,000-5,999 0.00 6,000-8,999 0.00 6,000-8,999 0.00
BIN_04 3,000-3,999 0.00 6,000-7,999 0.00 9,000-11,999 0.00 9,000-11,999 0.00
BIN_05 4,000-4,999 0.00 8,000-9,999 0.00 12,000-14,999 0.00 12,000-14,999 0.00
BIN_06 5,000-5,999 0.00 10,000-11,999 0.00 15,000-17,999 0.04 15,000-17,999 0.00
BIN_07 6,000-6,999 0.00 12,000-13,999 0.01 18,000-20,999 0.09 18,000-20,999 0.02
BIN_08 7,000-7,999 0.00 14,000-15,999 0.04 21,000-23,999 0.15 21,000-23,999 0.05
BIN_09 8,000-8,999 0.02 16,000-17,999 0.08 24,000-26,999 0.21 24,000-26,999 0.09
BIN_10 9,000-9,999 0.04 18,000-19,999 0.14 27,000-29,999 0.28 27,000-29,999 0.14
BIN_11 10,000-10,999 0.08 20,000-21,999 0.22 30,000-32,999 0.35 30,000-32,999 0.20
BIN_12 11,000-11,999 0.12 22,000-23,999 0.30 33,000-35,999 0.43 33,000-35,999 0.27
BIN_13 12,000-12,999 0.18 24,000-25,999 0.40 36,000-38,999 0.53 36,000-38,999 0.34
BIN_14 13,000-13,999 0.24 26,000-27,999 0.51 39,000-41,999 0.64 39,000-41,999 0.42
BIN_15 14,000-14,999 0.31 28,000-29,999 0.62 42,000-44,999 0.76 42,000-44,999 0.52
BIN_16 15,000-15,999 0.40 30,000-31,999 0.75 45,000-47,999 0.92 45,000-47,999 0.62
BIN_17 16,000-16,999 0.49 32,000-33,999 0.89 48,000-50,999 1.10 48,000-50,999 0.73
BIN_18 17,000-17,999 0.59 34,000-35,999 1.04 51,000-53,999 1.32 51,000-53,999 0.85
BIN_19 18,000-18,999 0.71 36,000-37,999 1.21 54,000-56,999 1.58 54,000-56,999 0.99
BIN_20 19,000-19,999 0.85 38,000-39,999 1.40 57,000-59,999 1.90 57,000-59,999 1.14
BIN_21 20,000-20,999 1.01 40,000-41,999 1.63 60,000-62,999 2.27 60,000-62,999 1.30
BIN_22 21,000-21,999 1.19 42,000-43,999 1.90 63,000-65,999 2.71 63,000-65,999 1.47
BIN_23 22,000-22,999 1.41 44,000-45,999 2.23 66,000-68,999 3.22 66,000-68,999 1.66
BIN_24 23,000-23,999 1.67 46,000-47,999 2.63 69,000-71,999 3.82 69,000-71,999 1.87
BIN_25 24,000-24,999 1.99 48,000-49,999 3.13 72,000-74,999 4.51 72,000-74,999 2.10
BIN_26 25,000-25,999 2.38 50,000-51,999 3.74 75,000-77,999 5.30 75,000-77,999 2.35
BIN_27 26,000-26,999 2.85 52,000-53,999 4.49 78,000-80,999 6.20 78,000-80,999 2.63
BIN_28 27,000-27,999 3.43 54,000-55,999 5.42 81,000-83,999 7.22 81,000-83,999 2.93
BIN_29 28,000-28,999 4.12 56,000-57,999 6.56 84,000-86,999 8.37 84,000-86,999 3.26
BIN_30 29,000-29,999 4.96 58,000-59,999 7.95 87,000-89,999 9.66 87,000-89,999 3.62
BIN_31 30,000-30,999 5.97 60,000-61,999 9.64 90,000-92,999 11.09 90,000-92,999 4.02
BIN_32 31,000-31,999 7.18 62,000-63,999 11.67 93,000-95,999 12.68 93,000-95,999 4.46
BIN_33 32,000-32,999 8.62 64,000-65,999 14.11 96,000-98,999 14.44 96,000-98,999 4.94
BIN_34 33,000-33,999 10.33 66,000-67,999 17.00 99,000-101,999 16.37 99,000-101,999 5.47
BIN_35 34,000-34,999 12.35 68,000-69,999 20.43 102,000-104,999 18.48 102,000-104,999 6.06
BIN_36 35,000-35,999 14.72 70,000-71,999 24.47 105,000-107,999 20.78 105,000-107,999 6.71
BIN_37 36,000-36,999 17.48 72,000-73,999 29.19 108,000-110,999 23.28 108,000-110,999 7.42
BIN_38 37,000-37,999 20.70 74,000-75,999 34.68 111,000-113,999 25.98 111,000-113,999 8.20
BIN_39 38,000-38,999 24.41 76,000-77,999 41.04 114,000-116,999 28.90 114,000-116,999 9.06
BIN_40 ≥ 39,000 28.70 ≥ 78,000 48.37 ≥ 117,000 32.03 ≥ 117,000 10.01

Note: this table was developed to work with LTPP DD_AX tables. DARWin-METM has a different definition of the first load range. For DARWin-METM, the first load bin range is 0-2,999 lb for single axles, 0-5,999 lb for tandem axles, and 0-11,999 lb for tridem and quad axles. Impact factors for the first three or four bins depending on axle group type should be averaged. For single and tandem axles, value from BIN_04 corresponds to DARWin-METM BIN_02 and so on. For tridem and quad axles, value from BIN_05 corresponds to DARWin-METM BIN_02 and so on.

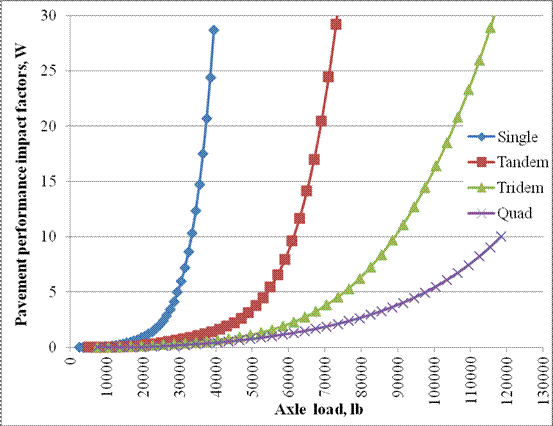
Figure 6. Graph. Pavement performance impact W factors. This graph shows pavement performance impact factors. The y-axis represents the number pavement performance impact factors, and the x-axis represents the axle load ranges in pounds. There are four series of points shown in the plot that correspond to single, tandem, tridem, and quad axles. All four series of points resemble J-shaped curves and show a steep increase in the pavement performance impact factors with increase in axle load ranges. Data points for the four series of points are represented as follows: blue diamond markers for single, red square markers for tandem, green triangular markers for tridem, and purple x-shaped markers for quad axles. The maximum pavement performance impact factors for the various axle types range from a little over 10 for quad axles, 28.7 for single axles, and over 30 for tridems and quads.

Figure 6. Graph. Pavement performance impact W factors.

CONCLUSIONS BASED ON MEPDG ANALYSIS OUTCOMES

Based on findings from MEPDG sensitivity analyses, the W factor is very low or zero for low load ranges, especially below 50 percent of the legal load limit, and it increases rapidly as load ranges go over the legal limit. This conclusion is valid for pavement structures designed for typical truck flows (vehicle class distributions (VCDs) and truck volumes) observed on RI and ROPA roads based on observation of MEPDG-predicted load-related distresses for typical flexible and rigid pavement structures.

EXAMPLE DEMONSTRATING IMPORTANCE OF HEAVY AXLE LOADS FOR PAVEMENT DESIGN

From the pavement design perspective, an evaluation of the entire NALS is not necessary since it is the higher load intervals of the NALS where the decisions need to be made in establishing default NALS for pavement design. The following example demonstrates this concept. Figure 7 shows four distinctly different NALS for class 9 tandem axles. Two of the sites are from the SPS TPF WIM study, and two are from the LTPP GPS. All data were obtained from LTPP MEPDG traffic tables for sites that passed minimum data availability requirements for research-quality data and LTPP traffic QC checks designed for SPS and GPS sites. Loading patterns at these four sites are summarized as follows:

Figure 7. Graph. Tandem NALS for class 9 vehicles for four LTPP sites. This graph shows tandem plot of tandem normalized axle load spectra (NALS) for class 9 vehicles for four Long-Term Pavement Performance (LTPP) sites. The x-axis shows the tandem axle load ranges in pounds, and the y-axis shows percentage of tandem axles. There are four series of lines shown in the figure that correspond to the various loading patterns. There is also a black vertical line at 34,000 to 35,999 lb that corresponds to the legal limit. The line for site #1: 35-0500 is represented by a continuous purple line and purple square markers and has a peak of a little over 7 percent at 20,000 to 21,999 lb and a second peak of 3.5 percent at 32,000 to 33,999 lb. The line for site #2: 12-0100 is represented by a continuous black line and black diamond markers and has a peak of 6.5 percent at 14,000 to 15,999 lb and a second peak of 9.5 percent at 30,000 to 31,999 lb. The line for site #3: 50-1004 is represented by a continuous green line and green circular markers and has a peak of 10 percent at 10,000 to 11,999 lb and a second peak of 3.5 percent at 32,000 to 33,999 lb. The line for site #4: 44-7401 is represented by a continuous blue line and blue triangular markers and has a peak of 13 percent at 12,000 to 13,999 lb and a second peak of 2.5 percent at 40,000 to 41,999 lb.

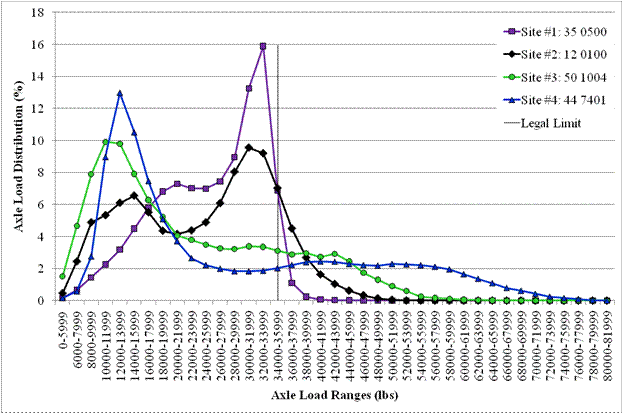
Figure 7. Graph. Tandem NALS for class 9 vehicles for four LTPP sites.

If one considers the portion of NALS distribution below the legal limit for tandem axle loads, then looking at load distribution, site 1 would be considered the heaviest, followed by sites 2, 3, and 4. However, if one considers the portion of NALS distribution above legal limit for tandem axle loads, then the opposite trend would be observed.

Another important observation is that GPS sites (sites 3 and 4) have the longer tail for the heavier load bins, which was noted as a reason why the MEPDG global NALS was questioned-MEPDG NALS are based on data from GPS sites. NALS for sites 3 and 4 result in higher levels of predicted distress and require thicker pavement layers than the MEPDG default NALS (discussed in the following paragraphs).

These four loading patterns were used in the MEPDG software to predict bottom-up alligator cracking, rutting, and IRI for a typical AC pavement section located in a southern climate (Alabama SPS-6). Figure 8 through figure 10 show the predicted load-related distresses and IRI against the number of tandem axle load applications. As can be seen in the plots, site 4 consistently performed the worst, followed by sites 3, 2, and 1. This would be opposite to the expected trend if load spectra characterizations would be based on the loading distributions observed below legal load limits but in line with the loading distributions above the legal limit. The sudden jumps in predicted distresses are caused by seasonal environmental effects and annual truck volume growth function.

This graph shows Mechanistic-Empirical Pavement Design Guide (MEPDG) alligator cracking prediction. The x-axis shows the number of truck applications for class 9, and the y axis shows percentage of alligator cracking from 0 to 35 percent. There are four series of lines shown in the figure that correspond to the various loading patterns. The line for SPS site 35-0500 is represented by a continuous purple line and purple square markers for data points and starts with an alligator cracking value of 1.56 percent at 150,000 truck applications and jumps to 1.71 percent at 1,050,000 truck applications, 2.56 percent at 1,500,000 truck applications, 2.89 percent at 1,956,000 truck applications, 4.06 percent at 2,892,000 truck applications, 12.51 percent at 3,360,000 truck applications, 13.97 percent at 3,834,240 truck applications, and 16.08 percent at 4,807,680 truck applications. The line for SPS site 12-0100 is represented by a continuous black line and black diamond markers for data points and starts with an alligator cracking value of 1.58 percent at 150,000 truck applications and jumps to 1.75 percent at 1,050,000 truck applications, 2.99 percent at 1,500,000 truck applications, 3.62 percent at 1,956,000 truck applications, 6.05 percent at 2,892,000 truck applications, 16.54 percent at 3,360,000 truck applications, 17.57 percent at 3,834,240 truck applications, and 18.96 percent at 4,807,680 truck applications. The line for GPS site 50-1004 is represented by a continuous green line and green circular markers for data points and starts with an alligator cracking value of 1.62 percent at 150,000 truck applications and jumps to 1.84 percent at 1,050,000 truck applications, 4.93 percent at 1,500,000 truck applications, 7.02 percent at 1,956,000 truck applications, 12.51 percent at 2,892,000 truck applications, 20.39 percent at 3,360,000 truck applications, 20.81 percent at 3,834,240 truck applications, and 21.38 percent at 4,807,680 truck applications. The line for GPS site 44-7401 is represented by a continuous blue line and blue triangular markers for data points sand tarts with an alligator cracking value of 2.06 percent at 150,000 truck applications and jumps to 3.77 percent at 1,050,000 truck applications, 22.89 percent at 1,500,000 truck applications, 23.59 percent at 1,956,000 truck applications, 25 percent at 2,892,000 truck applications, 28.21 percent at 3,360,000 truck applications, 28.71 percent at 3,834,240 truck applications, and 29.61 percent at 4,807,680 truck applications. A horizontal red line for the terminal condition is at 25 percent all the way across the plot.

Figure 8. Graph. MEPDG alligator cracking prediction.

Figure 9. Graph. MEPDG total rutting prediction. This graph shows the Mechanistic-Empirical Pavement Design Guide (MEPDG) total rutting prediction. The x-axis shows the number of truck applications for class 9, and the y-axis shows the total rutting from 0 to 0.9 inch. The lines are step-shaped, with alternating horizontal and vertical segments. There are four series of lines shown in the figure that correspond to the various loading patterns. The line for SPS site 44-7401 is represented by a continuous blue line and blue triangular markers for data points and starts with a rutting value of 0.39 inch at 150,000 truck applications and jumps to 0.42 inch at 1,050,000 truck applications, 0.67 inch at 1,500,000 truck applications, and 0.79 inch at 3,360,000 truck applications. The line for SPS site 12-0100 is represented by a continuous black line and black diamond markers for data points and starts with a rutting value of 0.27 inch at 150,000 truck applications and jumps to 0.29 inch at 1,050,000 truck applications, 0.48 inch at 1,500,000 truck applications, and 0.57 inch at 3,360,000 truck applications. The line for GPS site 50-1004 is represented by a continuous green line and green circular markers for data points and starts with a rutting value of 0.3 inch at 150,000 truck applications and jumps to 0.33 inch at 1,050,000 truck applications, 0.52 inch at 1,500,000 truck applications, and 0.61 inch at 3,360,000 truck applications. The line for GPS site 35-0500 is represented by a continuous purple line and purple square markers for data points and starts with a rutting value of 0.25 inch at 150,000 truck applications and jumps to 0.28 inch at 1,050,000 truck applications, 0.48 inch at 1,500,000 truck applications, and 0.54 inch at 3,360,000 truck applications. A horizontal red line for the terminal condition is at a rutting value of 0.75 inch all the way across the plot.

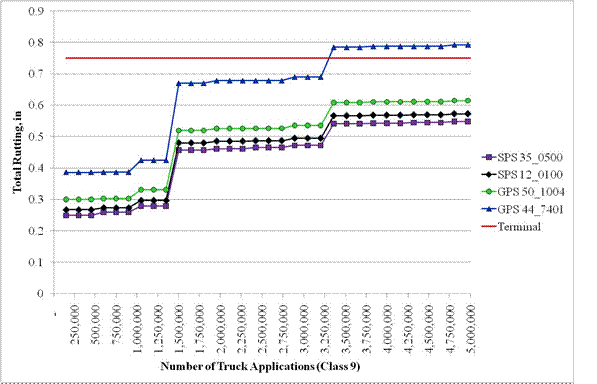
Figure 9. Graph. MEPDG total rutting prediction.

Figure 10. Graph. MEPDG IRI prediction. This graph shows the Mechanistic-Empirical Pavement Design Guide (MEPDG) International Roughness Index (IRI) prediction. The x-axis shows the number of truck applications for class 9, and the y-axis shows the IRI from 60 to 180 inches/mi. The lines are step-shaped, with alternating horizontal and vertical segments. There are four series of lines shown in the figure that correspond to the various loading patterns. The line for SPS site 44-7401 is represented by a continuous blue line and blue triangular markers for data points and starts with an IRI value of 102.89 inches/mi at 150,000 truck applications and jumps to 105.53 inches/mi at 1,050,000 truck applications, 120.56 inches/mi at 1,500,000 truck applications, and 130.25 inches/mi at 3,360,000 truck applications. The line for SPS site 12-0100 is represented by a continuous black line and black diamond markers for data points and starts with an IRI value of 96.74 inches/mi at 150,000 truck applications and jumps to 98.53 inches/mi at 1,050,000 truck applications, 107.91 inches/mi at 1,500,000 truck applications, and 114.11 inches/mi at 3,360,000 truck applications. The line for GPS site 50-1004 is represented by a continuous green line and green circular markers for data points and starts with an IRI value of 98.37 inches/mi at 150,000 truck applications and jumps to 100.26 inches/mi at 1,050,000 truck applications, 110.16 inches/mi at 1,500,000 truck applications, and 116.98 inches/mi at 3,360,000 truck applications. The line for GPS site 35-0500 is represented by a continuous purple line and purple square markers for data points and starts with an IRI value of 95.86 inches/mi at 150,000 truck applications and jumps to 97.63 inches/mi at 1,050,000 truck applications, 106.67 inches/mi at 1,500,000 truck applications, and 112.38 inches/mi at 3,360,000 truck applications. A horizontal red line for the terminal condition is at an IRI value of 172 inches/mi all the way across the plot.

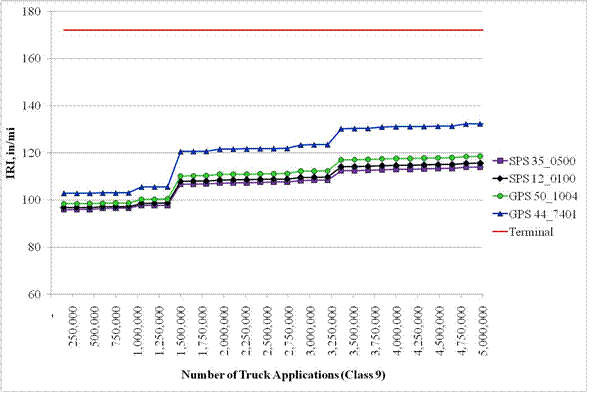
Figure 10. Graph. MEPDG IRI prediction.

These results clearly demonstrate the importance of heavy loads (or overloads, in this example) for pavement design and the relative unimportance of lighter loads. More importantly, the error within the heavier load intervals is what impacts pavement design and where the emphasis on accuracy needs to be focused. Large errors within the lighter load intervals are likely to have a negligible impact on pavement thickness design.

The key question is, what load level significantly impacts pavement thickness design? Based on limited sensitivity analysis, the 75th percentile level of the legal axle load and the number or percentage of axles exceeding the axle load limit can be used as a rule-of-thumb criterion. However, this load level or interval can depend on material, structure, climate, and MEPDG transfer function (the relationship between stress or strain and the resulting pavement damage).

It should be noted that this example is provided for illustrative purposes only. Traffic input data obtained for the GPS sites may be incorrect. For example, for site 1, (SPS site 1) there are few tandem axles exceeding 40,000 lb, the maximum allowable weight on split tandem axles. However, over 10 percent of tandem axles for site 4 exceed 50,000 lb. Such high occurrence of extreme overloads is very unusual, and the data may be suspect.

 

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse | U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101