MEPDG Traffic Loading Defaults Derived From Traffic Pooled Fund Study

CHAPTER 6-Analysis of Axle Load Spectra Variability USING SPS TPF WIM Data

OBJECTIVE AND SCOPE

The objective of the analyses presented in this chapter was to evaluate the effect of different data availability and data quality scenarios on load spectra reliability using LTPP SPS TPF data.⁽²⁾ The findings from these analyses are useful to support the definition of data quality (precision and bias) and availability criteria, as well as the procedures to minimize errors when determining the NALS for MEPDG use.

LTPP has developed and implemented procedures to mitigate some types of errors affecting WIM data reliability, such as WIM system performance requirements and minimum number of monitoring days. However, it is not possible to avoid some gaps in data coverage when equipment malfunctions and some days of the month have missing data. The following types of statistical analyses were conducted to help evaluate the impact of different sources of error on reliability of axle load spectra estimates:

• Evaluation of errors due to WIM equipment precision and bias.
  
  
• Evaluation of errors associated with different data availability scenarios.
  
  
• Evaluation of temporal consistency and reasonableness in traffic loading data.

EVALUATION OF ERRORS ASSOCIATED WITH WIM EQUIPMENT PRECISION AND BIAS

Consideration of WIM Precision and Bias for Pavement Design

SPS TPF WIM data must conform to the ASTM E1318-02 specification for type I WIM system accuracy detailed in table 2.⁽¹²⁾ Accuracy in axle weight measurements is evaluated by errors associated with WIM measurement precision and bias.

In the context of this study, WIM bias is the difference between the expected axle load value (average of all measurements) measured by the WIM equipment and the true axle load value (measured by static scale). Bias is determined as deviation of the mean axle weight error from zero. The WIM calibration process seeks to minimize bias in axle weight measurements. ASTM E1318-02 requires bias in all weight measurements to be approximately zero.⁽¹²⁾

Precision refers to the WIM equipment's ability to reproduce an axle load measurement consistently. Precision is defined by a maximum axle weight error expected for a specified CL. For a type I WIM system, the maximum allowable axle weight error is up to ±20 percent of the true value for single axles over 12,000 lb and up to ±15 percent for tandem, tridem, and quad axles over 25,000 lb for 95 percent conformance. WIM equipment precision is a function of WIM technology, maintenance, sensor array, and site conditions.

Precision or bias errors may have a potential impact on resulting axle load spectrum. However, the effects of bias and precision on the estimated load spectrum are different as follows:

• The accuracy level can theoretically cause a shift in the spectrum; however, the expected shift is relatively small if there is no bias because of the compensation of precision-related errors once different loads are combined in a single load bin. Some loads are measured higher, while some are measured lower than the true value. On average (i.e., when thousands of axle load applications collected over the year are combined), they are measured correctly if there is no bias. This is the principle behind the central limit theorem: the loads are measured with some error however the central tendency leads to correct average values, particularly when traffic volume is high. When the annualized NALS are built, the average number of axles in multiple load bin categories is used.
  
  
• Bias may result from calibration drift and equipment undercalibration (underestimation of weights) or overcalibration (overestimation of weights). If a WIM system has a significant calibration drift (over 5 percent error in heavy axle loads due to bias alone), the resulting load spectrum will be shifted and may have a significant impact on pavement performance predictions, as will be demonstrated in the ensuing sections.

Both precision and bias represent deviations from the true axle load value, and for the analyses conducted in this study, these differences are represented as percentage differences from the true static weight. For this study, a 95 percent CL was used to compute the representative bias and precision values based on data obtained from field validation and calibration reports for each SPS TPF site. This CL indicates that 95 percent of all observed precision and bias values were lower than the representative values selected for the analyses. Therefore, these values represent a conservative estimate of precision and bias. The reason for selecting the conservative estimate is to make sure that the conclusion obtained using these values would apply to a majority of observations based on LTPP WIM calibration data.

Analysis Purpose

Among the sources of variability of axle load spectra, WIM precision and bias have the potential to cause errors relative to the true distribution of axle loads for a highway section. In this study, researchers investigated the impact of precision and bias on MEPDG estimates to check if WIM measurements based on existing LTPP field calibration criteria may negatively influence predictions of pavement performance.

The starting point for the analyses was to define representative levels of precision and bias of WIM equipment using historical data from field calibrations for the 26 LTPP SPS TPF WIM sites.

Data Used

To estimate the representative values of WIM system precision and bias values and to investigate the effect of WIM system precision and bias associated with axle weight measurements, WIM data collected during routine WIM field calibrations for 26 LTPP SPS TPF WIM sites were obtained and analyzed. This included both pre- and post-calibration data collected during each field validation visit. Only periods (years and months) that had sufficient WIM data for developing MEPDG load spectra (based on data availability and data reasonableness criteria presented later in this report) were considered in this analysis. No pre-calibration data from the initial WIM installation were included in the analysis. The number of calibration visits for each site varied from two to eight.

During each calibration session, axle weight data from 40 passes of the calibration trucks (20 runs by each of 2 calibration trucks, primarily class 9 trucks) were collected as part of pre- and post-calibration axle weight measurement accuracy assessment.

Representative Bias

Historical WIM calibration data were used to calculate the differences between actual and measured axle loads and GVW for each calibration truck. These values were used to estimate the bias of WIM measurements for the 26 sites for each field calibration visit. In addition, changes in bias values between calibration visits were evaluated, and average bias values were computed for each site and each period between calibration visits. The distribution of average WIM system biases observed between calibration cycles among all SPS TPF sites is shown in figure 19. All distributions are centered close to zero and do not show any strong skewness.

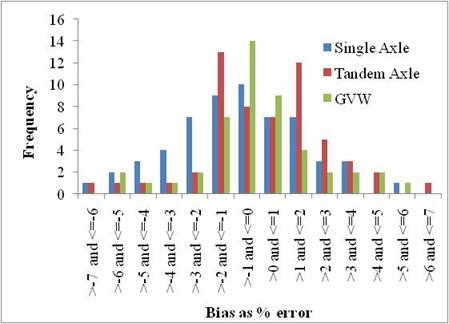
Figure 19. Graph. Distribution of average WIM system biases observed between calibration cycles among all SPS TPF sites.

The percentile differences between the actual and measured loads were averaged to estimate the bias for each site between two consecutive calibration visits. These values were then averaged over all calibrations for the site to estimate the average bias. Average bias values were computed separately for single and tandem axles for each site.

The probability distributions (characterized by the standard deviation and the average) of bias values for single and tandem axles computed for each site were used to estimate representative bias values with 95 percent confidence. The representative bias values computed for tandem axles also were used in the later analyses to represent bias of other multi-axle groups, like tridem and quads.

Once the average and standard deviation of bias for the 26 sites were established, a hypothesis test was performed to check if the overall bias was zero, considering all 26 WIM sites. This hypothesis was accepted. Assuming the overall bias representing all sites is zero, the 95 percent confidence interval was calculated, and the limits provided a conservative value for bias to use in Monte Carlo simulations and MEPDG analysis. The results indicate that, for 95 percent of all observations, the bias did not exceed approximately ±3.9 percent for single axle load measurements and ±3.5 percent for tandem axle load measurements.

Representative Precision

Precision is normally described as the largest error expected with a certain level of confidence, usually 95 percent. To estimate this value, it is necessary to use the standard deviation or variance associated with the measurement errors. The following procedure describes how the variances of the percentile differences between actual and measured axle loads obtained during WIM calibration sessions were used to estimate representative WIM precision values observed at SPS TPF sites.

The standard deviation for the percent differences between actual and measured axle loads obtained during each calibration session provided an estimate of precision achieved for the site. For an individual site, two values of standard deviations (one before and one after calibration) were computed based on 40 calibration truck measurements. Each of these values was squared to estimate the precision variances. Next, the pooled variance using all the variances obtained during individual calibration sessions was calculated to represent the typical precision variance for each site (based on two to eight variance values obtained from multiple calibration sessions), as follows:

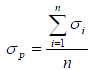
Figure 20. Equation. Pooled variance for a site.

Where:

σ_p = Pooled variance for a site.

σ_i = Precision variance obtained for each sample (in this case, for each pre- or post-calibration set of 40 test truck measurements).

n = Number of variance estimates used in the calculation (total number of pre- and post-calibration datasets for a given site, n varies from two to eight for different sites).

With 26 variance estimates (one for each site) the overall pooled variance was calculated using the same formula, with n representing the total number of sites (n = 26) and σ _i representing the precision variance calculated for each site. The overall pooled variance (16.2 for single axle and 12.1 for multiple axles) was calculated from a sample of WIM site calibrations, and it represents the sample variance.

To infer a representative variance for precision error, a CF was applied to the sample variance to ensure that in 95 percent of the cases, the population variance was below the assumed value based on the sample. To estimate the population variance with 95 percent confidence, it was assumed that the sample variance followed a chi-square probability distribution. With the sample size of 113 variance estimates, considering all pre- and post-calibration estimates for all sites used in this analysis, a chi-square test was conducted to estimate the one-sided 95 percent confidence interval for the variance. This limit (20.5 for a single axle and 15.3 for multiple axles) was assumed to represent a conservative value for the precision variance representing the 26 sites analyzed. Table 8 provides a summary of representative precision variance and bias values computed for individual SPS TPF sites.

The population variance with 95 percent confidence based on 26 sites was used to estimate the maximum precision error. To estimate this value, the standard deviation was computed as being the square root of the population variance and then multiplied by the standard deviate for 95 percent confidence.

Table 9 presents a summary of maximum percentile axle load errors associated with conservative estimates of SPS TPF WIM precision and bias. The expected maximum error due to precision alone is 8.9 percent for single axles and 7.7 percent for tandem axles. The expected total maximum error is obtained by summing both the precision and bias errors, each with 95 percent confidence. These values represent conservative values for precision and bias, as more than 95 percent of all observations are expected to be lower than these values. These values are 12.8 percent for single axles and 11.2 percent for tandem axles-well below the LTPP accuracy criteria of 20 and 15 percent for single and tandem axles, respectively.

Effect of WIM Precision and Bias on Load Spectra Accuracy

Data Selection

The effect of WIM precision and bias on reliability of monthly NALS estimates was evaluated for selected SPS WIM sites that exhibit different levels of data variability to investigate the significance of this effect. To cover the range of observed daily variability in percentages of heavy axles, a set of sites was selected for the analysis that correspond to 50th, 75th, 95th, and 99th percentiles of all other observations with respect to observed variability in daily percentages of heavy tandem axles. For example, 50 percent of all the observed variations in daily percentages of heavy tandem axle counts are lower than the variation observed at site 8-0200 for the month of April 2009. A summary of the selected sites is shown in table 10. These sites cover a range of geographical locations as well as daily volumes and axle load spectra distributions.

Analysis Process

To check the impact of precision and bias on the reliability of monthly NALS, the research team conducted a Monte Carlo simulation analysis using a sample of 31 days (1 month) of continuous WIM data for four different LTPP sites. The following three scenarios were evaluated:

• Precision and no bias.
  
  
• Precision and positive bias.
  
  
• Precision and negative bias.

The precision and bias levels used in this analysis are shown in table 8. These are conservative estimates based on SPS TPF sites. It was expected that more than 95 percent of all sites would have maximum axle weight errors due to WIM equipment precision and bias less than the percentages shown in table 8.

In addition, the researchers tested two data availability scenarios: 7 and 31 days. The reason for testing different data availability scenarios in combination with precision and bias is that the combined error is likely to increase due to permutation of individual errors.

The Monte Carlo simulation was used to simulate different data availability and precision and bias scenarios using procedures described in chapter 5. The results of analysis are summarized in table 11.

Analysis Findings

Using table 11, the effect of precision alone can be evaluated using the unbiased scenario for data available for all days of the month. It is noted that errors associated with both precision and bias can be more important than the number of days surveyed, if data for at least 7 days are available. The difference in PWLE between 7 and 31 days provides the basis for this conclusion because the levels of precision and bias are similar in both cases.

To evaluate the amount of error caused by WIM equipment precision and bias alone, the results for monthly data availability scenarios where all 31 days of data were available were used. It can be noted that when bias is introduced, PWLE increases no matter if the bias is positive or negative. Based on the results presented in table 11, the following conclusions can be made:

• As expected, PWLE decreased as the number of days surveyed increased. In general, a decrease lower than 1.5 percent in the total error was achieved when comparing 7 days surveyed to the full month. The small error difference between the full month and 7 days confirms that data collected during 1 week is representative of the spectrum for the month.
  
  
• The impact of precision can only be assessed by observing PWLE estimated for the case of no bias and 31 days of data available in a month. PWLE for the four sites investigated ranged from 0.7 to 3.4 percent, which is considered small. The precision values used in the analysis were representative of the upper end of all precision errors calculated from calibration reports for SPS TPF sites. Therefore, this conclusion could be considered representative for the precision levels observed in SPS TPF data. Because precision-related errors tend to compensate each other when all the available data are considered in calculation of representative annual axle load spectrum, the impact of these errors on estimated pavement performance is low.
  
  
• The impact of bias on PWLE ranged from 1.0 to 3.5 percent and is considered low for the typical bias values found in the LTPP sites (see table 8). The impact of bias alone can be evaluated by comparing the results for the 31 days surveyed. Because bias can cause greater differences in pavement performance estimates using the MEPDG, the impact of bias was further investigated in this study using the MEPDG analysis presented later in this chapter.
  
  
• The impact of negative and positive bias was similar among different sites; however, the values vary slightly due to differences in the NALS.
  
  
• PWLE proved to be useful to quantify the effect and relative importance of precision, bias, and sample size. The impact of these three effects would be very difficult to assess without a parameter like PWLE because it accounts for the load distribution as a whole, the performance weights for each load level, and the errors associated with the percentage for each load bin in the spectrum.

It is important to note that this analysis was conducted using conservative estimates of axle weight errors due to WIM equipment precision and bias values applied to LTPP sites. This was done to investigate the effect of precision and bias for sites with different data variability and different axle load spectra.

Effect of WIM Precision and Bias on MEPDG Outcomes

The research team investigated the effect of precision and bias on the NALS estimates and associated MEPDG outcomes. The goal of the analysis was to evaluate whether typical precision and bias values observed at LTPP SPS TPF WIM sites were likely to produce significant differences in MEPDG outcomes. The results of the analysis could be used to confirm current WIM accuracy requirements or to provide information for refinement.

Development of NALS for MEPDG Analysis

NALS obtained as the average of all SPS TPF sites (global default) was selected as the baseline (unbiased) load spectra for the analysis. Monte Carlo simulation was used to generate the load spectra for positive and negative bias. To do that, positive and negative bias percentages provided in table 9 (3.9 percent error due to bias for single axles and 3.5 percent error due to bias for multiple axles) were applied to each load bin value. In addition to bias, errors resulting from limited precision of WIM devices were also accounted for (8.9 percent precision error for single axle weight measurements and 7.7 percent error for multiple axle weight measurements). Examples of resulting single and tandem axle load spectra for class 9 vehicles are shown in figure 21 and figure 22. Similar adjustments were made to load spectra for all other vehicle classes and axle group types used in the analysis.

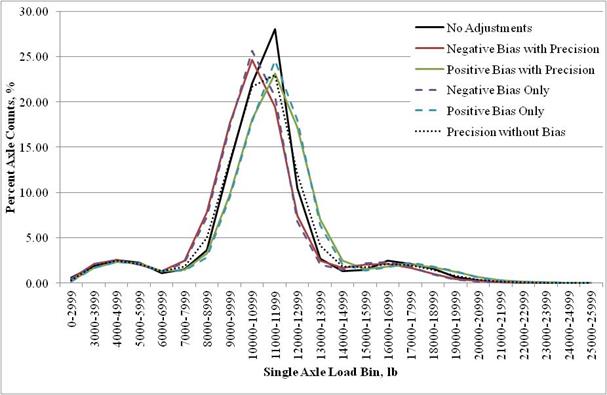
Figure 21. Graph. Example of biased single axle load spectra for class 9 vehicles.

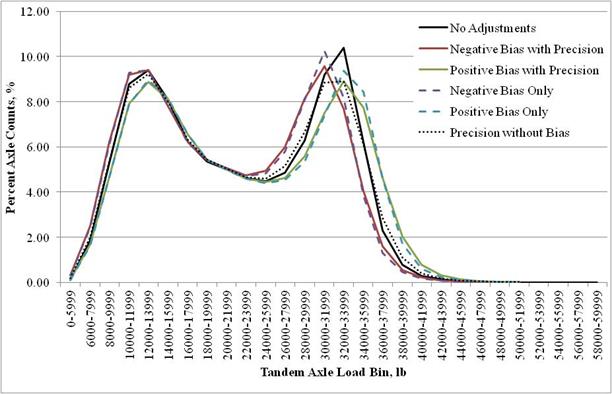
Figure 22. Graph. Example of biased tandem axle load spectra for class 9 vehicles.

MEPDG Designs

The research team developed a set of representative rigid and flexible pavement designs and analyzed the predicted pavement performance. Table 12 presents a summary of the pavement design structures used for this analysis. VCDs and AADTT values characteristic to RI and ROPA roads were used for the analyses and represent typical values observed in LTPP database for rigid and flexible pavements.

Note: Top-down cracking was used in the analysis. However, there is extensive debate in the pavement engineering community on the applicability of the mechanism included in the MEPDG for top-down cracking predictions. The Mechanistic-Empirical Pavement Design Guide, Interim Edition: A Manual of Practice, suggests using top-down cracking predictions for information purposes and not to make changes to the designs.⁽¹⁾

In the sensitivity analysis, a pavement was first designed using NALS without adjusting for precision and bias and then analyzed again using load spectra adjusted for negative and positive bias, as well as with and without precision adjustment to see the differences in pavement design life predictions. To analyze the difference in pavement thickness resulting from different load spectra, changes were made to the top structural layer (AC or PCC) only. For this analysis, MEPDG results computed for 90 percent design reliability and pavement performance criteria specified in the MEPDG version 1.1 software were used.

MEPDG Analysis Findings

To evaluate the results of the analysis, the following criteria were used: results were considered significantly different if pavement life was reduced by at least 20 percent (3 years for flexible pavements and 4 years for rigid pavements) or if the thickness difference in the AC or PCC structural (top) layer was more than 0.5 inch. Table 13 and table 14 show the results of MEPDG sensitivity analysis for the design life and layer thickness scenarios, respectively.

N = No adjustment.
P = Precision only.
NBP = Negative bias + precision.
PBP = Positive bias + precision.

The results show that when either negative or positive bias was introduced to axle load spectra, the resulting differences in pavement life were close but not over the selected threshold criterion of 20 percent difference in pavement design life, compared to results using axle load spectra with no bias. When pavement life predictions were compared for the cases with positive versus negative bias, half of design cases showed difference in pavement design life over the 20 percent criterion.

With respect to observed differences in pavement thickness, only one design case (rutting for flexible RI) showed significant difference when the no bias design case was compared with the positive bias design case. When pavement thickness predictions were compared for the cases with positive versus negative bias, again only the rutting case showed a difference in AC thickness over the 0.5-inch criterion. This was primarily due to rutting in unbound layers and subgrade, and this type of rutting is not expected to be mitigated by adjusting the thickness of the surface layer. It has been found that the MEPDG overpredicts the amount of rutting in the unbound layers and subgrade. Local calibration factors less than unity have been recommended to reduce the amount of rutting in those layers.

With respect to WIM measurement precision evaluation for the precision values tested, no MEPDG results indicated differences in pavement life or thickness that would be considered significant from a practical point of view.

Additional MEPDG Analysis of 5 Percent WIM Bias

Since bias potentially contributes to significantly different MEPDG outcomes, a decision was made to increase bias values to 5 percent to see if this would result in significantly different MEPDG outcomes. Bias values of 5 percent or more were observed in a few instances at SPS TPF sites before WIM calibration was conducted, indicating changes in axle weigh measurement accuracies between calibration visits. Table 15 and table 16 show a summary of MEPDG results considering 5 percent bias.

No = No bias.
NB = Negative bias.
PB = Positive bias.

The results from this analysis show that when a negative or positive bias of 5 percent is introduced to the axle load spectra, the resulting differences in estimated pavement life for all cases were different but not over the selected threshold criterion of 20 percent difference in pavement design life compared to results using axle load spectra with no bias. When pavement life predictions were compared for cases with positive and negative bias, all but one design case (joint faulting for rigid ROPA) showed a significant difference in pavement design life over the 20 percent criterion.

With respect to observed differences in pavement thickness, only one design case (rutting for flexible RI) showed a significant difference when the no-bias design case was compared with the positive and negative bias design cases. When pavement thickness predictions were compared for the cases with positive versus negative bias, three of five flexible pavement design cases showed a difference in AC thickness over the 0.5-inch criterion, while no rigid designs showed differences at or above 0.5 inch.

Conclusions from Analysis of WIM Precision and Bias

SPS TPF WIM data were assessed, and it was determined through statistical analysis that for 95 percent of the data, the average error in axle weight measurements due to WIM bias observed between calibration visits was 3.9 percent or less for single axles and 3.5 percent or less for tandem axles. The expected maximum error due to precision was found to be 8.9 percent for single axles and 7.7 percent for tandem axles using 95 percent confidence. These observations are based on the historical data collected during field calibration visits under the SPS TPF study (from 2003 to 2011).

These conservative estimates of expected errors due to WIM precision and bias were used to estimate PWLE for selected LTPP sites representing different axle load spectra. The observed errors in monthly axle load spectra estimates varied based on axle load spectra shapes and daily data variability. None of the estimates exceeded 7 percent in PWLE. MEPDG analysis of selected pavement designs did not show significant differences in MEPDG outcomes for these levels of error. Based on these findings, it is possible to infer that, using current ASTM and LTPP SPS TPF calibration procedures, the level of errors caused by WIM equipment precision and bias is likely to be insignificant for MEPDG applications.⁽¹²⁾

However, the statistical analysis and MEPDG sensitivity analyses presented in this section indicate that it is beneficial to develop and enforce acceptance criteria for maximum allowable weight measurement bias for individual axles to ensure that good quality data are used to define the load spectrum for MEPDG applications. MEPDG analysis indicates that bias exceeding 5 percent of mean error could lead to significant differences in MEPDG design outcomes. It is recommended that mean error in axle weight measurements of calibration trucks should stay below 5 percent to ensure good quality data for pavement design.

Through MEPDG analysis, it was also determined that different MEPDG outcomes could be observed for under- versus over-calibrated WIM systems. This case represents real-life situations when an under-calibrated WIM system is over-calibrated in subsequent visits. However, when load spectra from multiple calibration cycles are combined, the errors in the over- or under-calibrated load spectra will likely compensate each other.

Based on the analysis of data from WIM site calibration reports, it is evident that bias values change between calibration visits. LTPP recognizes this and mitigates it through cyclic annual calibrations. However, because it is cost prohibitive to calibrate more than once a year, some level of bias in the data is inevitable between calibrations. To mitigate the effect of bias in development of axle load spectra for MEPDG applications, it is beneficial to have the data collected for the period covering multiple calibration cycles. This way, the effect of the bias is minimized by averaging data from the months that had different biases within the year and between years.

EVALUATION OF ERRORS ASSOCIATED WITH DATA AVAILABILITY

Analysis Purpose

The extent of data coverage (number of days per year/month/DOW) and procedures used to derive axle loading estimates from the available data affect the reliability of NALS estimates. A considerable amount of work has been done in this area through previous studies that analyzed the effects of various traffic data collection scenarios on the accuracy of traffic estimates.^(6,13) For this study, a number of analyses were conducted to evaluate the impact of data availability on the expected error (represented by PWLE) in NALS estimates using SPS TPF WIM data. The purpose of the analysis was to obtain information that could be used to define data availability criteria and computational procedures for developing default NALS estimates.

Effect of Daily Data Availability on Monthly NALS Estimates

Data Used

The researchers developed a dataset to aid in the analysis of the impact of daily data availability on computed monthly NALS values. Specifically, the analysis focused on scenarios with high variability in heavy axle percentages in NALS, as accuracy in these values matters most for pavement design applications. The analysis focused on tandem axles, as these axles carry the majority of heavy axle loads observed at SPS TPF sites.

To select a representative dataset for analysis, variability in daily percentages of heavy tandem axle loads was evaluated for the 26 SPS TPF sites for all months and all years. All the months of data for all SPS TPF sites that had daily counts for every day of the month were included in this evaluation.

Heavy axle load percentages were computed using NALS by summing percentages of axles in load bins that represent heavy loads. Two different definitions of heavy loads were considered: one that includes all load bins at or above the legal load limit value for a given axle group type and one that includes all load bins above 75 percent of legal load limit value for a given axle group type. The initial analysis was based on an evaluation of consequences of variability in daily percentages of overloaded axles on monthly NALS estimates. However, the limitation of this analysis approach was a very low percentage of tandem axles with overloads typically observed at SPS TPF sites. Therefore, it was decided to expand the definition of heavy loads from legal limit to 75 percent or more of the legal limit in further analyses.

Analysis of Heavy Axle Loads Variability

Variability in daily percentages of heavy axle loads was evaluated by comparing standard deviations in daily percentages of heavy axles computed for each month for each SPS TPF site. The distribution of standard deviations in daily percentages of heavy axles with respect to daily axle counts is shown in figure 23.

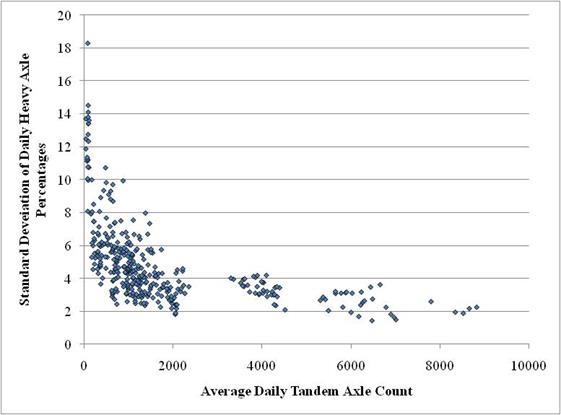
Figure 23. Graph. Distribution of standard deviations of daily heavy tandem axle percentages.

Based on analysis of SPS TPF data, it was found that sites with low daily axle counts generally had much higher variability in daily percentages of heavy axle counts. Two of the SPS TPF sites with consistently highest variability also had the lowest overall volume of tandem axle loads-sites 4-0100 and 12-0500.

Selection of Representative Sites for Analysis

To cover the range of observed daily variability in percentages of heavy axles, a set of sites was selected for a detailed analysis of different data availability scenarios. The selected sites and months of data correspond to 50th, 75th, 95th, and 99th percentiles of all other observations with respect to observed variability in daily percentages of heavy tandem axles. For example, 50 percent of all the observed variations in daily percentages of heavy tandem axle counts were less than variation observed at site 8-0200 for the month of April 2009. Table 17 summarizes the selected sites, which cover a wide spectrum of geographical locations and daily volumes.

For each of the four selected data samples, different data availability scenarios (from 2 to 31 days per month) were simulated using the Monte Carlo method and the procedure described in figure 14. Using the simulation results, PWLE values were computed for different data availability scenarios. A reliability level of 95 percent for PWLE was used in this analysis. In other words, the representative error was expected to be within ±PWLE in 95 percent of the cases. This analysis did not account for errors associated with precision and bias of WIM equipment.

Analysis Results

Results from the Monte Carlo simulations for different data availability scenarios are shown in table 18. As can be seen, the PWLE value decreased as the number of monitoring days increased. The decrease in PWLE was small for data availability over 7 days.

Conclusions

For all the cases evaluated, there was a significant drop in the error of monthly NALS estimate when 7 or more consecutive days of WIM data were available for each month. This trend is observed whether the variability of heavy loads was higher or lower. Therefore, availability of data for 7 days in a month was found to be a good conservative criterion to ensure the errors associated with daily data availability were small when estimating monthly axle load spectra.

Another conclusion is that the PWLE parameter is helpful to assess the variability associated with the whole load spectrum (all axle load levels and axle group types considered). For site 26-0100, PWLE for 7 days availability scenario was higher compared to the other sites despite the fact that for this site, the variability of heavy tandem axle loads was not the highest. This is the result of the combined effect of the full range of loads and axle group types on the PWLE value.

Effect of Seven Consecutive Versus Non-Consecutive DOW on Monthly NALS Estimates

Another analysis was carried out to evaluate the impact of using data from 7 consecutive or non-consecutive DOW. In this analysis, each DOW was randomly selected from the full month of data using Monte Carlo simulation until every DOW (Sunday through Saturday) was represented at least once in the 7-day sample. PWLE errors were computed separately for the consecutive and random 7 DOW samples.

The results of this analysis indicate that while the use of consecutive days resulted in slightly lower errors in NALS estimates, the differences in PWLE were relatively small and had little practical impact on the accuracy of monthly NALS estimates. For example, for site 27-500 that exhibited daily data variability typical for SPS TPF sites, the difference in PWLE error between consecutive and non-consecutive 7 DOW was less than 1 percent, as shown in figure 24.

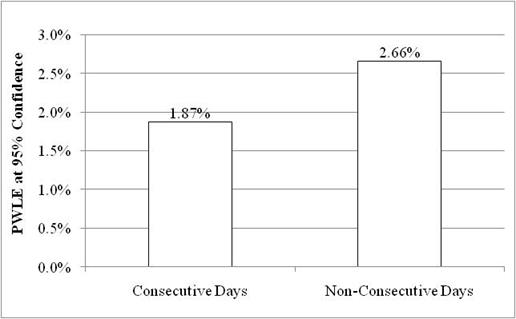
Figure 24. Graph. PWLE at 95 percent confidence for 7 consecutive and non-consecutive DOW for site 27-0500.

Effect of Monthly Data Availability on Annual NALS Estimates

Twelve Consecutive Versus Non-Consecutive Months

Despite the availability of SPS TPF WIM data over several years, there are some gaps in monthly data coverage, either due to equipment malfunction during certain periods or because data were filtered out during the data QC review process. Sometimes, a given month could be missing for 1 year but available for the next year. Therefore, it was necessary to evaluate the impact of using non-continuous monthly data in the development of RANALS (i.e., estimate of NALS based on all years and all months with available high quality SPS TPF WIM data). The data are averaged in several steps: first to develop a DOW estimate for each month, then to develop an estimate for each month, and finally to develop a representative annual estimate considering all available years and months.

In this case, the analysis was conducted using data from site 51-0100 as seed data for the simulation. This site was selected as an example based on the availability of 30 continuous months of data (one of the longest continuous monitored periods without gaps in monthly data summaries) and higher data variability due to relatively low truck volume.

Two types of simulation were performed to estimate the annual NALS based on data from 12 of the 30 months of data. In the first scenario, data for one January, one February, and so on were picked up at random from the 30 months until the data included each of the months in a year regardless if they were from the same year or not. This scenario was called "any random month." For the second scenario, the first month of data was randomized, and data for the 11 consecutive months from the starting month were used to estimate the load spectrum. This scenario was called "continuous months." The PWLE results for 95 percent confidence for both scenarios were comparable, and both PWLEs were lower than 0.8 percent, indicating that for practical purposes, the difference between having consecutive and non-consecutive months in a period of 2.5 years can be considered very low.

Traffic loading patterns may differ from year to year due to changes in national and local economic conditions. Therefore, for each site, it is beneficial to use all available years of data to develop RANALS to account for potential year-to-year variability. However, if multiple years of data are unavailable or if only several partial years are available, data still could be used for NALS generation if, as a minimum, representative loading estimates can be obtained for 12 calendar months from available acceptable quality data and any potential outliers are identified and removed based on temporal analysis of monthly NALS (see procedures provided later in this chapter).

These conclusions are based on the analysis of data collected over a period of 30 months. It is not possible to say for certain if these conclusions will hold for data collected many years ago due to the fact that traffic loading patterns may change over time.

Multiple Years Versus 12 Monthly Values

The benefit of using multiple years of data versus a sample of 12 months was evaluated using statistical analysis techniques. No site-specific data were used for this analysis because the goal was only to evaluate the trend in PWLE as the amount of available data increased. The scenario assumed a generic site having a PWLE value of 3 percent if data for more than 60 months were available to compute this parameter and low variability in monthly NALS estimates that typically is observed among SPS TPF WIM sites.

In this case, PWLE based on different monthly data availability scenarios can be estimated using the following equation in figure 25:

Figure 25. Equation. Actual PWLE for the site.

Where:

PWLE_n = Value estimated for n months of data.

t_{n - 1,p} = Student t-value for a sample size of n - 1 degrees of freedom and CL p.

PWLE_act = Actual PWLE for the site.

The results of the analysis for 95 percent confidence are shown in figure 26. It demonstrates that the error range for a selected level of confidence decreases when more months of data are available for the PWLE estimate. Assuming the actual PWLE with 95 percent for a site is 3 percent, after 12 months of data, the difference from the true PWLE is very small. Moreover, using at least 12 months of data will take into consideration any seasonality in the traffic pattern. Based on the trend shown in figure 26, use of less than 12 months is possible provided there is compelling evidence supporting an assumption of the low month-to-month variation in NALS; however, use of less than 4 months will lead to high PWLE values due to the small sample size.

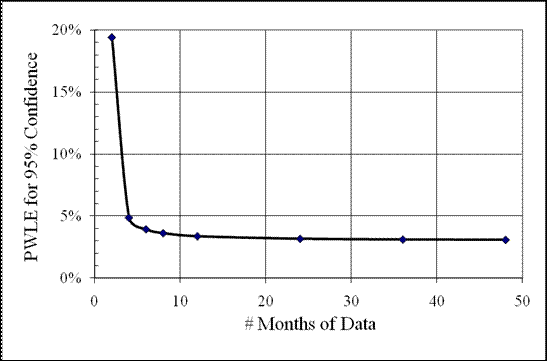
Figure 26. Graph. PWLE trend with data availability (in months of data).

Conclusions from Analysis of WIM Data Availability

The analysis of different data availability scenarios indicates that the following data availability criteria will minimize error due to limited data availability and assure high accuracy of monthly and annual NALS estimates based on SPS TPF WIM data:

• Availability of at least 1 of each 7 DOW per month to avoid potential DOW bias. Days do not need to be consecutive.
  
  
• Availability of at least 1 of each 12 calendar months to avoid potential seasonal bias. Months do not need to be consecutive or from the same calendar year. (Use of data collected more than 4 years apart was not investigated and is not recommended at this time.)

These criteria apply to the development of site-specific monthly and annual NALS estimates for individual sites and based on analysis of errors associated with the total axle load spectrum that considers all truck classes (FHWA classes 4 through 13) and all axle group types (single, tandem, tridem, and quad). However, for the individual vehicle classes and axle group types that have low percentages in a given VCD (such as vehicle classes 7, 11, 12, and 13), the errors in NALS may be higher than for well-represented classes and axles due to higher variability of axle loads and lower data availability.

These criteria may be considered too conservative for roads that do not exhibit high seasonality or high DOW variability in normalized axle load distributions. For such roads, analysis of temporal consistency could be used to determine lesser minimum data availability requirements on a case-by-case basis.

EVALUATION OF TEMPORAL CONSISTENCY AND REASONABLENESS IN TRAFFIC LOADING DATA

Analysis Purpose

The purpose of the analysis was to identify data that may represent accurate WIM counts but atypical loading condition for a given site. In addition, this analysis provided means of carrying out verification checks for the WIM data that already passed LTPP QC checks.

The analysis focused on evaluating the stability in monthly NALS over time for individual sites and identifying load distributions that differ significantly from other monthly load distributions for each site. Identified outliers were further investigated to identify potential reasons for atypical trends. The results were reported to LTPP using feedback reports. The researchers performed limited analysis of daily data for the cases where biases in monthly data summaries were found.

Analysis Scope

This analysis focused primarily on evaluating the differences in single and tandem monthly NALS for class 9 vehicles, which were found to be the dominant heavy vehicle class for all SPS TPF sites. The decision to use NALS for class 9 vehicles was based on the following reasons:

• Most of the heavy loads used in pavement design of interstate and principal arterial roads (road types associated with SPS TPF sites) come from class 9 vehicles.
  
  
• Characteristics of load distribution for class 9 vehicles, including peak loads and legal load limits, are well known, allowing for the development of QA checks to identify anomalies.
  
  
• Class 9 vehicles are used to calibrate WIM sites, so WIM sensors that are performing well should be able to capture class 9 loads accurately.

Single and tandem class 9 NALS were analyzed separately. Monthly NALS was considered an outlier if the spectrum was significantly different from other monthly NALS available for a given site. After outliers were identified using single and tandem class 9 load spectra, load spectra for all classes combined were additionally reviewed for single, tandem, tridem, and quad axle groups, and any additional anomalies were documented.

Analysis of outliers was performed in a two-step approach. First, several statistical parameters were computed and used to screen the data and flag potential outlier NALS using methods described in the next section. This step was automated. Second, a data analyst reviewed flagged load spectra using a systematic procedure to determine if the data represented true outliers. Based on the manual review, a decision was made to remove or to keep flagged load spectra from development of the defaults. If the load spectrum was removed, statistical parameters used in the outlier identification were then recomputed using the updated set of available monthly NALS, and the outlier identification process was repeated until no more outliers were identified.

Two automated procedures were used to flag potential outlier NALS based on the analysis of monthly NALS for class 9 single and tandem axles:

•  Analysis of cumulative absolute differences between individual monthly and average monthly NALS.
  
  
• Analysis of shift in individual monthly peak loads compared to average monthly peak.

Outliers based on the whole NALS distribution and outliers specific to distribution of heavy loads (over 75 percent of the legal limit) were identified and analyzed for each site. The following sections describe the procedures used to flag potential outliers.

Procedure to Analyze of Cumulative Absolute Difference between Individual and Average Monthly NALS

Cumulative absolute difference between individual and average monthly NALS is a statistic that allows for the identification of differences in monthly NALS distribution shapes. To compute this statistic, first, an average monthly NALS was computed by averaging all available monthly NALS for a given site, vehicle class, and axle group type. Then, the cumulative absolute difference between a given monthly NALS and the average monthly NALS was computed by summing the absolute differences computed for each load bin between a given month and the average monthly load frequencies. These cumulative absolute differences were computed for each month, separately for single and tandem class 9 NALS.

Figure 27. Equation. Cumulative absolute differences for month, m.

Where:

= Cumulative absolute differences for month m.

PctLoads_im = Load frequency for month m for bin i.

AvgPctLoads_im = Average load frequency for bin i.

i = Bin i.

m = Month.

n = Total number of bins in NALS.

Next, cumulative absolute differences computed for each month were used to compute the average and standard deviation of the cumulative absolute differences. This computation was carried out separately for single and tandem axle class 9 monthly NALS for each site.

Monthly NALS that had cumulative absolute differences that exceeded the value of the average cumulative NALS difference plus two standard deviations of cumulative absolute differences were flagged as potential outliers. Figure 28 presents this testing criterion mathematically.

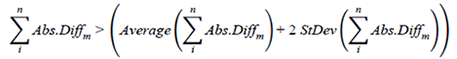
Figure 28. Equation. Cumulative absolute differences for m.

Where StDev = Standard deviation. All other variables have been previously defined.

This process was repeated iteratively by removing flagged months from the calculation of mean and standard deviation of the absolute cumulative differences, recomputing mean and standard deviation values, and identifying additional months that had absolute cumulative differences exceeding the recomputed mean plus two standard deviations. A data analyst reviewed the flagged months to make final outlier determination using a procedure described later in this chapter. An example of flagged outlier load spectra based on this procedure is shown in figure 29. In this example, NALS for October and December 2008 were flagged as outliers based on automated checks.

It should be noted that flagged data does not imply "bad" data. The default NALS should represent typical loading characteristics and not localized anomalies that occur for whatever reason. Thus, any outliers within the dataset should be removed. Potential outliers were not removed under NCHRP Project 1-37A, which probably caused some of the long tails in the NALS.⁽³⁾ Removal of the outliers is considered an improvement in simulating typical loading conditions at the regional or global levels.

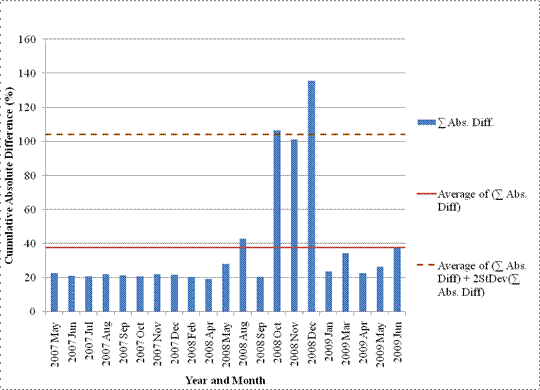
Figure 29. Graph. Comparison of absolute cumulative differences between average and monthly single axle NALS for site 05-0200 in Arkansas.

In addition to evaluating cumulative differences associated with the whole load spectrum, the same test was repeated using only the heavy loaded portion of the load spectrum. Heavy loads were defined as those that are 75 percent or more of the legal load limit for a given axle group type.

Analysis of Shift Between Individual Monthly and Average Peak Load

Peak load was identified separately for single and tandem axle group types for each monthly class 9 NALS for each site. Peak load corresponds to the load bin in which maximum load frequency is observed in the NALS. For consistency, the low value of the NALS load bin was used to identify the load bin. For example for a single axle load, if peak load was observed in a load bin defined as 11,000 to 11,999 lb, a value of 11,000 lb was used as the peak value. After peak load was computed for each month, the average peak load value was computed based on all available months.

Monthly NALS were flagged as a potential outlier if a peak load for a given month was outside of the range bound by the average peak load plus/minus two load bins. In LTPP tables, the load bin for single axle NALS is set to 1,000 lb, and the load bin for tandem axle NALS is set to 2,000 lb. An example of flagged outlier load spectra based on this procedure is shown in figure 30. Circled peak values represent outliers, as their values are below the average peak load minus two load bins (for November and December 2008).

Through analysis of peak load values for class 9 vehicles considering all SPS TPF sites, it was found that for single NALS, peak load corresponds to steering axle load for all SPS TPF sites, with an average value (rounded to the nearest 1,000 lb) of 11,000 lb. For tandem NALS, only loaded peaks were considered in the analysis, with an average value of 30,000 lb (corresponding to the beginning of the 2,000-lb load bin interval. Thus 30,000-lb value represents load bin from 30,000 to 32,000 lb).

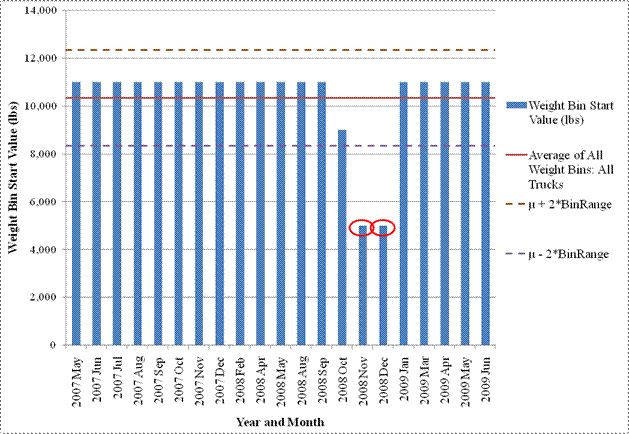
Figure 30. Graph. Comparison of monthly peak loads for single axles for site 05-0200 in Arkansas for class 9 vehicles.

Procedure for Manual Checks of Monthly NALS

The research team developed several manual checks to guide the data analyst in manual review of the potential monthly NALS outliers flagged through automated statistical outlier screening, as described in the following paragraphs.

Class 9 Single Axle NALS Manual Check

The class 9 single axle NALS manual check is as follows:

1. The peak load bin for the flagged months should be within the range defined by the peaks for all other months (excluding flagged months) for the same site. If peak loads for all available months cover a range of several bins, flagged spectra should have the peak within this range. In addition, sites that have monthly single axle load peaks range greater than four load bins should be flagged as sites with inconsistent single axle NALS. An example of outlier load spectra is shown in figure 31.
   
   
2. The peak load bin should be within a range bound by 11,000 lb ±2,000 lb. This range was established based on analysis of peak loads for all 26 SPS TPF sites. An example of typical peak range is shown in figure 31.
   
   
3. Cumulative percentage of overloaded axles (over 20,000 lb) should be within a range bound by the mean ±3 standard deviations of cumulative percentage of overloaded axles computed using data for all the months for a given site.
   
   
4. Cumulative percentage of overloaded single axles for class 9 should be below 1 percent, typically observed for SPS TPF sites class 9 single axles. This value was established based on analysis of class 9 single axle overloads for all 26 SPS TPF sites and is equal to the mean percentage of overloads plus two standard deviations computed based on 26 SPS TPF sites. If a high percentage of overloads is observed, the number of single and tandem axles per truck should be checked to see if the high number of single axles per class 9 trucks indicates the presence of split-tandem axles classified as singles.
   
   

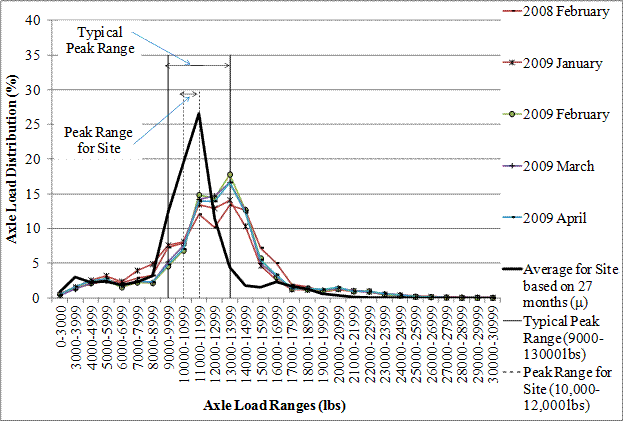
Figure 31. Graph. Monthly NALS for single axles for SPS site 26-0100 class 9 trucks.

Class 9 Tandem Axle NALS Manual Check

The class 9 tandem axle NALS manual check is as follows:

1. For a site with no defined seasonality in axle load distributions, load bins corresponding to the loaded peak should have a similar monthly value. For a site with seasonal variation in axle load distributions, peak loads for all available months cover a range of several bins; all spectra should have the peak within this range (spectra flagged during automated outlier screening are excluded from computation of the range). If a peak for flagged spectrum is outside of loaded peak bin or range of bins, it is considered an outlier. An example of outlier load spectra for several months in 2009 is shown in figure 32.
   
   
2. Sites that have a range of monthly loaded peaks greater than four load bins should be flagged as sites with inconsistent tandem axle NALS, unless they have a repeatable seasonal pattern for different loaded peak bins.
   
   
3. The peak load bin should be within a range bound by 30,000 lb ±4,000 lb. An example of outlier load spectra is shown in figure 32. This example demonstrates that for a period from January through April 2009, the majority of fully loaded class 9 tandem axles shifted into the illegal overloads category, which represents a very different load distribution compared to the 27 distributions available for the other months with data for this site. This is a possible but highly unlikely scenario. A more plausible explanation is WIM system malfunction. Analysis of single axle load spectra for this site presented in figure 31 indicated similar shifts in single axle load peak loads, supporting the conclusion regarding WIM system malfunction or calibration drift (since steering axle loads for class 9 vehicles are not likely to become heavier during 4 out of 27 monitoring months). The fact that both unloaded and loaded peaks in the tandem axle distribution shifted also is indicative of a likely calibration shift.
   
   
4. Cumulative percentage of overloaded axles should be within a range bound by mean ±3 standard deviations of cumulative percentage of overloaded axles computed using data for all the months for a given site.
   
   

Figure 32. Graph. Monthly NALS for tandem axles for site 26-0100 class 9 trucks.

Additional Manual Checks for All Classes Combined

In addition to class 9 single and tandem checks of monthly NALS, the following checks were conducted:

1. Review combined (classes 4 through 13) axle load distribution plots for each axle group (single, tandem, tridem, quad) and visually identify monthly NALS that have shape different from the other months and from the average NALS shape computed based on all the months. Note these atypical distributions in the outlier report table.
   
   
2. Review axle load distribution plots for each axle group and identify monthly NALS that have higher percentages of very low weight loads (the first two load bins in each distribution). Note these atypical distributions in the outlier report table.
   
   
3. For sites where class 9 is not a dominant truck class, review consistency in load spectra for the dominant heavy vehicle classes (classes 4 and 6 through 13).
   
   

Results of Traffic Loading Data Temporal Consistency and Outlier Analysis

Data available in LTPP SDR 24 LTAS database table MM_AX were used to construct monthly NALS and used in temporal consistency and outlier analysis. Detailed results of traffic loading data temporal consistency and outlier analysis outcomes are presented in appendix A for the automated and manual checks described in the preceding sections. Table 19 provides a summary of types of outliers observed and the amount of data flagged as a result of outlier analysis. As can be inferred, most outliers were identified as distributions that have excessive cumulative absolute difference in NALS (i.e., different shape of load distribution) and addition had load peaks (single and/or tandem class 9) outside typical range for a given site.

As a result of the outlier analysis, 12 percent of all months with WIM data included in the SDR 24 dataset for SPS TPF sites were removed from further data analysis. Sites that had large number of outliers include the following:

• OH 39-0100: Excluded 8 of 30 months, all 2004 (27 percent).
  
  
• FL 12-0500: Excluded 21 months of 53 months, all 2005 and 2006 (40 percent).
  
  
• MI 26-0100: Excluded 8 months of 35 months (23 percent).

Table 20 summarizes sites that have unusually high percentages of light loads for classes 4 and 6 through 13. Class 5 was excluded from this evaluation, as low loads were expected for this class. None of the class 9 vehicles had high percentages of light loads. Evaluating the high percentage of light loads can reveal vehicle classification problems whereby passenger vehicles or passenger vehicles pulling trailers are classified as truck.

Note: Blank cells indicate that no instances were recognized.

Procedures to Evaluate Axle Group Type and Number of Axles per Truck Reasonableness

Accurate axle group type and number of axles per truck are important input parameters for computing the total number of axle load applications for MEPDG analysis. These two parameters, in combination with vehicle class volumes and growth rates, are used to transform NALS into total axle loading input used in the MEPDG. The following sections describe reasonableness checks for these two parameters.

Axle Group Type Checks

Axle group types reported for individual vehicle classes were reviewed to identify atypical axle group types for each class using the LTPP vehicle classification scheme. Axle group type QC checks by class included the following:

• Class 4: Should have either two single axles or a single and a tandem axle.
  
  
• Class 5: Majority of class 5 vehicles should have two single axles, with the exception of lightweight single unit trucks pulling a trailer (note that the Traffic Monitoring Guide does not allow trailers on class 5, while the LTPP scheme does).⁽¹⁴⁾
  
  
• Class 6: Should have a single and a tandem axle.
  
  
• Class 7: Should have a single and a tridem or a quad axle. Tandems are possible per the LTPP classification scheme but atypical based on vehicles' physical configuration.
  Also, future data may have five or more axles per the updated 2012 LTPP classification scheme.
  
  
• Class 8: Should have single and tandem axles. Tridems are possible per the LTPP classification scheme but atypical based on vehicles' physical configuration.
  
  
• Class 9: Should have one single and two tandem axles, three single axles and one tandem axle, or two single and one tridem axle. Quads are possible per the LTPP classification scheme but atypical based on vehicles' physical configuration.
  
  
• Class 10: Could have single, tandem, tridem, and quad axles.
  
  
• Class 11: Should have single axles. Tandems are possible per the LTPP classification scheme but atypical based on vehicles' physical configuration.
  
  
• Class 12: Should have single and tandem axles.
  
  
• Class 13: Should have single, tandem, and can have triple and quad axles.

Atypical axle group types identified as a result of this review were reported to FHWA using feedback reports. A summary of the evaluation is presented in appendix B.

Number of Axles per Truck Checks

APC coefficients were computed for each site, vehicle class, and axle group type. These values depend on the vehicle classification algorithm, as well truck traffic composition at each site. Average number of axles per class computed based on the 26 SPS TPF sites (shown in table 21) were used as a basis for comparison with individual site values.

Summary of Results

The results of this evaluation are summarized as follows:

• Most unexpected APC values were observed for class 7 trucks (8 of 26 sites) due to higher-than-expected single and tandem values. However, there is some evidence that this is becoming a typical configuration for dump trucks transporting excavated material and gravel in many States. Therefore, these values were not flagged as atypical.
  
  
• About 50 percent of all APC flags were for SPS TPF sites in Ohio (39-0100 and 39-0200) and Washington (53-0200). This could be explained by the differences between the LTPP classification scheme and schemes utilized in the WIM systems installed by these States. In addition to unexpected APC values, these same States have the highest occurrences of very light axle weights for truck classes. This leads to a conclusion that these States implement the LTPP vehicle classification scheme with adjustments in the algorithm that allow different types of vehicles (mostly lightweight vehicles) to be classified as trucks.
  
  
• Site 39-0100 in Ohio is the only SPS TPF site with tridems reported for buses. This may be a case of misclassification, possibly because of aluminum dump trucks in Ohio having long axle spacing between the first and the second axles.