Long-Term Pavement Performance Program Determination of In-Place Elastic Layer Modulus: Backcalculation Methodology and Procedures

Chapter 3. Case Studies

The purpose of the case studies conducted in phase I of this project were twofold: (1) select the forward and/or backcalculation methods from the candidates identified in chapter 2 and (2) provide direction for automating the backcalculation process by establishing the decisionmaking criteria in evaluating the results. In addition, results from the case studies were used to confirm the rules of simulation in establishing the pavement structure on an automated basis.

LTPP Test Sections Selected for Case Studies

Test sections from the LTPP SPS and SMP experiments were selected because deflection basins for these experiments were measured at shorter time intervals than for the GPS experiments. Six case studies were used to compare and evaluate the candidate backcalculation and forward calculation programs and to demonstrate the different pre- and post-processing tools to be used for the production runs. The LTPP projects selected for the case studies are listed in table 2. The reasons for selecting these sites are as follows:

• Two of the case studies are LTPP SMP sites. The reason for selecting these seasonal sites was to estimate the variation in elastic modulus values over temperature and other seasonal changes as determined from deflection basins. One of the seasonal sites included in the demonstration is a rigid pavement (Utah 49-3011), and the other is a flexible pavement (Georgia 13-1005).
• Three case studies represent newly constructed pavements—two new construction flexible pavements from the SPS-1 experiment (Iowa and Wisconsin) and one new construction rigid pavement from the SPS-2 experiment (North Carolina). These projects were selected to include a wide range of layer thicknesses and materials for both pavement types.
• Two case studies represent rehabilitated or overlaid pavements—one from the SPS-5 experiment (rehabilitated flexible pavements) and one from the SPS-6 experiment (rehabilitated rigid pavements). The sections selected are from the Mississippi SPS-5 project to include varying HMA overlay mixtures (virgin and recycled asphalt pavement mixes) and layer thicknesses, while sections were selected from the Oklahoma SPS-6 project to include varying types of treatments to the existing PCC slabs.

Comparison of Results from Candidate Backcalculation Programs

This section provides a brief comparison of the results between the candidate backcalculation software packages in terms of the evaluation factors set forth in chapter 2. The BAKFAA and MICHBACK^© programs were dropped from further consideration because of issues encountered in executing large batch files for the first few case study sites.⁽¹⁰⁾ For the other four programs, three criteria were used in judging the acceptability of the results from the candidate forward and backcalculation methods: RMSE values, magnitude of the moduli, and comparison to laboratory-measured modulus values.

Deflection Basin Matching—RMSE

Figure 3 summarizes and compares the average RMSE values resulting from the backcalculation of layer moduli at each test section and day of testing. As shown, MODTAG^© consistently had lower RMSE values, while MODULUS consistently had higher RMSEs.^{1 (55)} Many of the MODTAG^© RMSE values were less than 1 percent. EVERCALC^© and MODTAG^© also had a higher percentage of stations with less than 2 percent RMSE. Based on the RMSE values, MODTAG^© and EVERCALC^© consistently resulted in a closer match between the measured and calculated deflection basins. The MODULUS program exhibited higher RMSE values in almost all cases for the two conditions: assuming the presence and absence of an apparent rigid layer or bedrock.

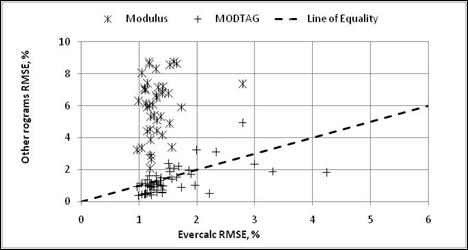
Figure 3. Graph. Comparison of RMSE values between backcalculation programs for flexible pavement sections comparing MODULUS, MODTAG^©, and EVERCALC^©.

Figure 4 summarizes and compares the average RMSEs from the best fit forward calculation method and EVERCALC^©. As shown, the RMSEs from the best fit method were significantly higher than from the EVERCALC^© program. This observation is in line with the authors’ experience from other projects with using the forward calculation equations based on the Hogg model for flexible pavements—the forward calculation program resulted in sets of layer moduli with significantly higher RMSE values than the backcalculation program.⁽²⁶⁾

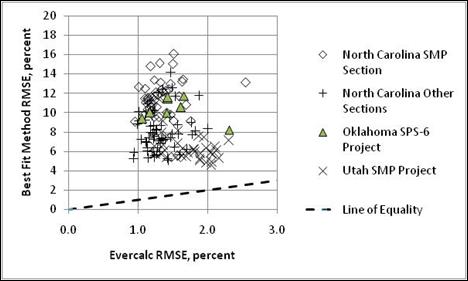
Figure 4. Graph. Comparison of RMSE values between backcalculation programs for rigid pavement sections comparing best fit method and EVERCALC^©.

Distribution of Elastic Moduli

The range of default elastic modulus values included in the MEPDG was used to define the initial acceptable range of elastic modulus values for comparing the results between different programs for different materials and soils.⁽¹⁾ The percentage of values within the acceptable range of moduli with RMSE less than 2 percent is summarized in the interim report for this project.⁽¹³⁾ EVERCALC^© exhibited a higher percentage of stations for which moduli were calculated within the typical range for the specific material in question. Backcalculated layer moduli for individual stations were outside the acceptable range of values, but the averages and majority of stations were within the range of typical values.

The distribution of resulting layer moduli for each layer during a day’s testing can be used to investigate the reasonableness of the results. Figure 5 shows the distribution of results for the crushed stone base material at the Georgia 13-1005 site, which exhibits a normal distribution. This type of distribution is typical of many pavement materials. In fact, many of the layers (bound and unbound) exhibit this type of distribution.

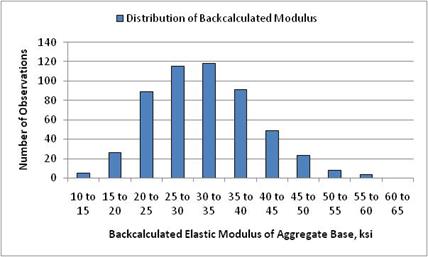
Figure 5. Graph. Normal distribution of calculated elastic modulus for a crushed stone base aggregate.

Conversely, figure 6 shows a bimodal distribution of results for the weathered soil layer at the Georgia 13-1005 site. A bimodal distribution can reflect a change in the results caused by changing material properties or thickness deviations along the section, compensating errors between two layers, and/or hitting a boundary condition or limit at multiple stations. Based on a review of previous backcalculated layer modulus values in the LTPP database, the results can also exhibit a uniform distribution.^(4,46) However, none of the test sections included in the case studies exhibited this type of distribution.

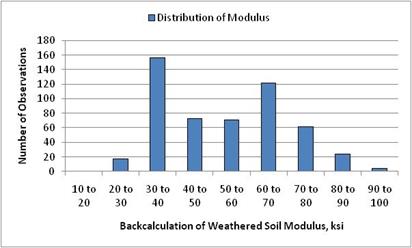
Figure 6. Graph. Bimodal distribution of calculated elastic modulus for the weathered soil layer.

Layer Stiffness Properties of Flexible Pavements

Figure 7 through figure 11 provide a comparison of the results from the candidate backcalculation methods in terms of elastic layer moduli for different layer or material types.

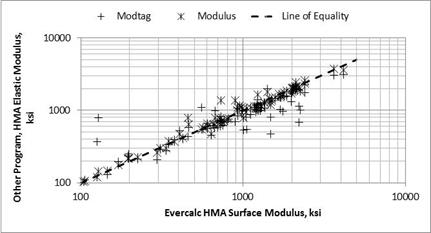
Figure 7. Graph. Comparison of backcalculated moduli from the candidate programs for the HMA layer.

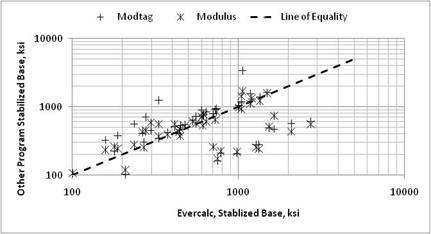
Figure 8. Graph. Comparison of backcalculated moduli from the candidate programs for the asphalt stabilized base layer.

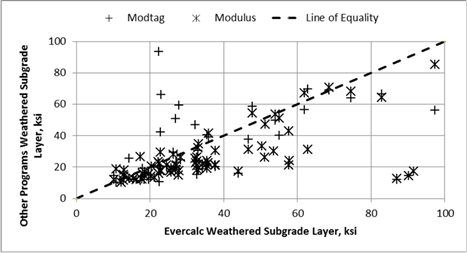
Figure 9. Graph. Comparison of backcalculated moduli from the candidate programs for the weathered soil layer modulus values.

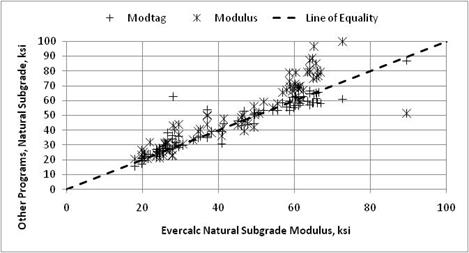
Figure 10. Graph. Comparison of backcalculated moduli from the candidate programs for the natural subgrade modulus values.

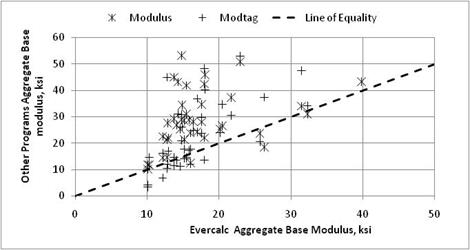
Figure 11. Graph. Comparison of backcalculated moduli from the candidate programs for aggregate base layers.

The following list summarizes the results related to selection of the backcalculation programs for flexible pavements:

• All three programs (EVERCALC^©, MODCOMP^©, and MODULUS) resulted in similar values with a lot less difference between the elastic layer moduli calculated by different procedures for the surface layer (figure 7) and subgrade (figure 10), regardless of the type of deflection basins.
• All three programs resulted in the same elastic layer moduli for the conditions when the deflection basins would be categorized as typical as defined by Von Quintus and Simpson and Von Quintus and Killingsworth.^(4,46) For the type II deflection basins, as defined by Von Quintus et al., the three programs resulted in different elastic layer moduli for the intermediate layers (i.e., the weathered soil layer and thinner aggregate base layers) (see figure 9 through figure 11).⁽⁴⁶⁾
• All three programs correctly identified some form of damage that was observed through forensic investigations or surface distress recorded in the LTPP database. Stripping, moisture damage, and debonding were identified as issues by all three programs.
• The MODULUS program consistently generated sets of layer moduli that exhibit much higher RMSE values than for EVERCALC^© and MODCOMP^©, while MODCOMP^© consistently resulted in slightly lower RMSEs than EVERCALC^© (see figure 3 and figure 4).

A t-test was used to determine if the average test day results from the two candidate programs with the lower RMSE values (EVERCALC^© and MODCOMP^©) were statistically indifferent. Table 3 provides a summary for a few of the test sections from three of the case studies. Both EVERCALC^© and MODCOMP^© resulted in indifferent elastic moduli for many of the test sections. About a fourth of the layers, however, resulted in statistically different datasets. The majority of the test sections with statistically different moduli were those for which the majority of the deflection basins are classified as type II.

Layer Stiffness Properties of Rigid Pavements

The primary material properties needed for completing a rigid pavement rehabilitation design or evaluation in accordance with the MEPDG are the k-value of the lower pavement layers and subgrade, the static elastic modulus for the PCC, and the resilient modulus of aggregate base layers.⁽¹⁾ The area and best fit closed form solution methods were used to estimate the elastic modulus of the PCC and aggregate base layers and the k-value for the combined lower pavement layers and subgrade.

Figure 12 includes a comparison of the elastic modulus calculated with EVERCALC^© and the moduli calculated using the area and best fit methods. As shown, the resulting elastic layer moduli from the EVERCALC^© program and the area method are variable but have minimal bias between the two. In addition, the unbonded condition of the best fit method has less bias than its bonded condition to EVERCALC^©. The bonded condition simply means the two layers are tied together, while the unbonded condition means the two layers are not tied together, and there is no shear transfer between the two layers. This brings up an issue of which method should be used in computing the elastic modulus of the PCC layer, the area or best fit method, as well as which condition should be simulated, bonded, or unbonded.

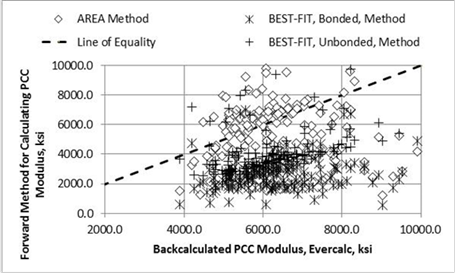
Figure 12. Graph. Backcalculated layer PCC modulus from EVERCALC^© compared to the elastic modulus calculated with the area and best fit methods.

The best fit method (unbonded condition) was selected for rigid pavements because it was used for global calibration for the MEPDG under NCHRP Project 1-37A.⁽⁵²⁾

Figure 13 and figure 14 show a comparison of results for the subgrade and aggregate base layers between EVERCALC^© and the best fit unbonded condition, while figure 15 shows a comparison of results for PCC layers. The best fit method resulted in significantly different or lower elastic layer moduli than EVERCALC^© for PCC (figure 12 and figure 15), while the bias was much less between the computed elastic layer moduli of the base layer between the best fit method and EVERCALC^© (figure 14).

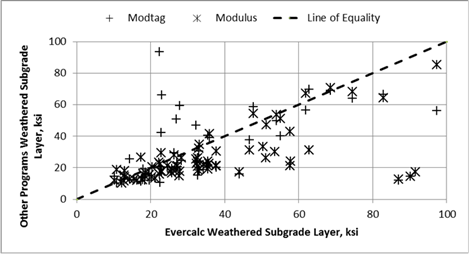
Figure 13. Graph. Comparison of forward and backcalculated moduli from the candidate programs for the subgrade layer.

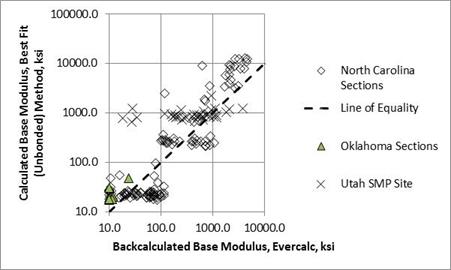
Figure 14. Graph. Comparison of forward and backcalculated moduli from the candidate programs for the aggregate base layer.

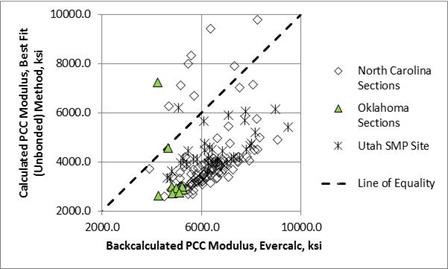
Figure 15. Graph. Comparison of forward and backcalculated moduli from the candidate programs for the PCC layer.

The t-test was used to determine if the average test day results from the forward and backcalculation programs were statistically indifferent. Table 4 provides a summary for a few of the test sections from three of the case studies for rigid pavements. As shown, the forward and backcalculation methods (best fit method and EVERCALC^©) resulted in significantly different PCC elastic moduli for most of the test sections, while about half of the test sections resulted in significantly indifferent elastic moduli for the base layer. This large bias between EVERCALC^© and the best fit method can have a critical impact in determining the PCC elastic modulus for input into the MEPDG.⁽¹⁾ This issue of bias is discussed further in the next section.

Field-Derived and Laboratory-Measured Layer Stiffness Properties

PCC Materials

Static elastic moduli for the PCC layers were extracted from the LTPP database. Figure 16 compares the laboratory-measured elastic moduli and backcalculated values for the PCC layers. As shown, the results from EVERCALC^© and the best fit method are highly variable in comparison to the measured PCC static modulus. The average elastic modulus ratio (i.e., E-ratio between the laboratory-measured and field-derived elastic moduli) for the PCC layer are as follows:

• EVERCALC^©: Mean E-ratio = 0.77; standard deviation = 0.176.
• Best fit method bonded: Mean E-ratio = 1.92; standard deviation = 1.254.
• Best fit method unbonded: Mean E-ratio = 1.00; standard deviation = 0.436.

Results from the EVERCALC^© program exhibited a coefficient of variation of 23 percent for the averages, which is much lower than the best fit method, which had a coefficient of variation of 65 percent for the bonded condition and 44 percent for the unbonded condition.

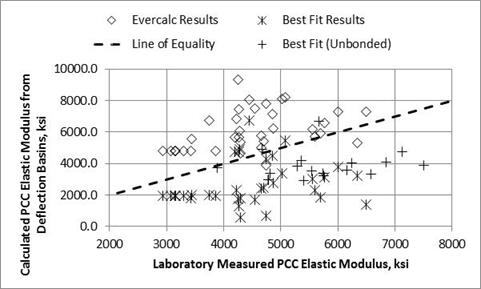
Figure 16. Graph. Comparison of backcalculated and laboratory-measured PCC moduli.²

The best fit bonded condition significantly underpredicted the measured values, while EVERCALC^© overpredicted the measured values. On average, the best fit unbonded condition resulted in no bias.

In summary, there is a significant difference between the resulting PCC elastic moduli from EVERCALC^© and the best fit method. The best fit unbonded condition resulted in an unbiased prediction of the laboratory-measured values. Assuming laboratory elastic moduli are used in the global or local calibration effort, an adjustment needs to be made to the EVERCALC^© dataset for use with the MEPDG software, similar to using the c-factor for unbound layers.^(45,46,1)

HMA and Bituminous Stabilized Materials

Backcalculated elastic layered moduli from deflection basins are used in the MEPDG for the rehabilitation and evaluation of flexible pavements.⁽¹⁾ Dynamic modulus values are estimated using the Witczak regression equation included in the MEPDG to represent the undamaged condition of HMA mixtures. These same values were calculated using the dynamic modulus regression equation from the MEPDG and included in the LTPP databases for the HMA and other bituminous layers.⁽¹⁾

Dynamic moduli for the HMA layers were extracted from the LTPP database. Figure 17 through figure 26 compare the laboratory estimated dynamic moduli and backcalculated values for the HMA layers. As shown, most of the backcalculation programs underpredict the laboratory-measured values for the loading frequency typically used for the FWD (25 Hz). All three backcalculation programs resulted in similar average values on a day of testing basis for many of the test sections, but not all.

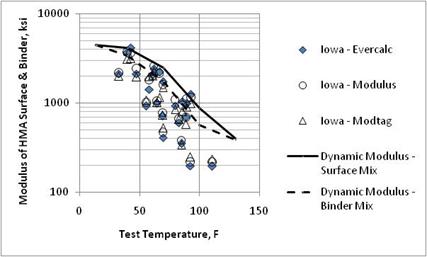
Figure 17. Graph. Comparison of backcalculated HMA surface and binder layer moduli and laboratory-measured moduli from the Iowa SPS-1 project.

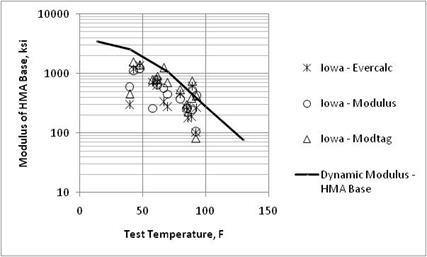
Figure 18. Graph. Comparison of backcalculated HMA base layer moduli and laboratory-measured moduli from the Iowa SPS-1 project.

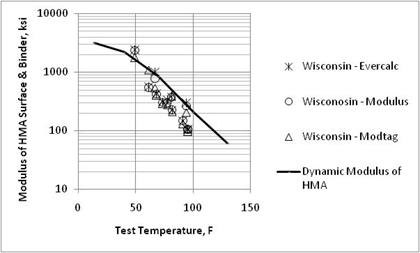
Figure 19. Graph. Comparison of backcalculated HMA surface and binder layer moduli and laboratory-measured moduli from the Wisconsin SPS-1 project.

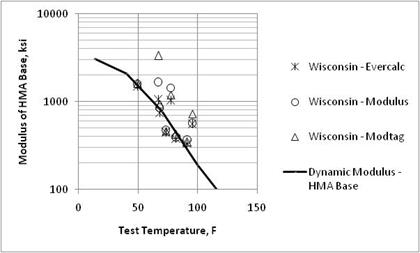
Figure 20. Graph. Comparison of backcalculated HMA base layer moduli and laboratory-measured moduli from the Wisconsin SPS-1 project.

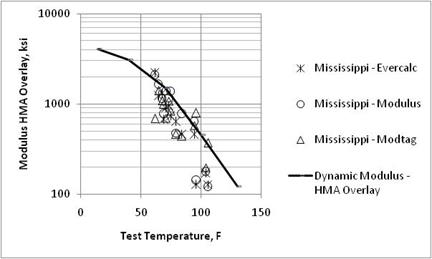
Figure 21. Graph. Comparison of backcalculated HMA overlay moduli and laboratory-measured moduli from the Mississippi SPS-5 project.

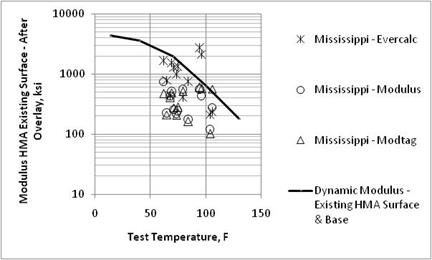
Figure 22. Graph. Comparison of backcalculated HMA surface layer moduli of the existing pavement after overlay placement and laboratory-measured moduli from the Mississippi SPS-5 project.

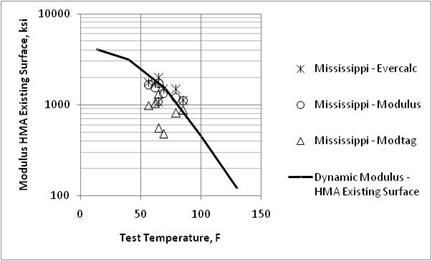
Figure 23. Graph. Comparison of backcalculated HMA surface layer moduli of the existing pavement prior to overlay placement and laboratory-measured moduli from the Mississippi SPS-5 project.

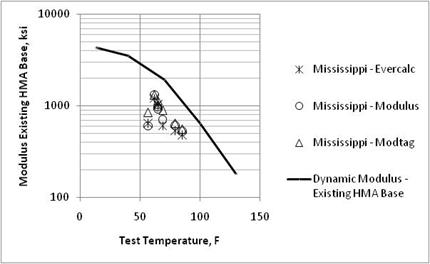
Figure 24. Graph. Comparison of backcalculated HMA base layer moduli of the existing pavement prior to overlay placement and laboratory-measured moduli from the Mississippi SPS-5 project.

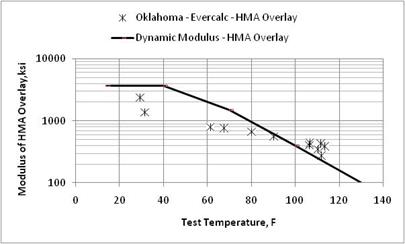
Figure 25. Graph. Comparison of backcalculated HMA moduli and laboratory-estimated dynamic modulus for the Oklahoma SPS-6 project.

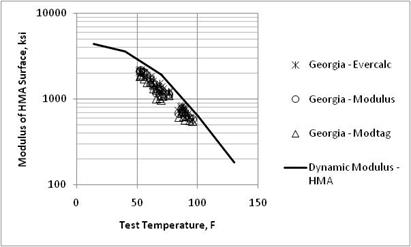
Figure 26. Graph. Comparison of backcalculated HMA moduli and laboratory-estimated dynamic modulus for the Georgia SMP project.

In summary, there is an insignificant difference between the resulting HMA elastic moduli from EVERCALC^©, MODULUS, and MODCOMP^©, but none of the programs resulted in unbiased predictions of the laboratory-measured values. This observation is important because it supports the MEPDG methodology for using FWD testing and backcalculated layer moduli of HMA layers for estimating the damage in those layers.⁽¹⁾ The sites that exhibited greater dispersion between the laboratory-estimated (undamaged dynamic moduli) and field-derived (damaged elastic moduli) moduli were found to have stripping or moisture damage and/or extensive cracking reported in the LTPP database.

Unbound Materials

Figure 27 through figure 29 compare the backcalculated elastic moduli from EVERCALC^©, MODULUS, and MODCOMP^©, respectively, and the laboratory-derived resilient moduli for each site for the weathered soil and subgrade layers. As shown, there is a lot of dispersion between the results, but the results are somewhat consistent with some of the earlier studies.^(45,46) The average c-factors calculated for the subgrade layers using the three candidate programs are as follows:

• EVERCALC^©: Average c-factor = 0.35; standard deviation = 0.136.
• MODCOMP^©: Average c-factor = 0.36; standard deviation = 0.146.
• MODULUS: Average c-factor = 0.41; standard deviation = 0.266.

Results from EVERCALC^© exhibited a coefficient of variation of 39 percent for the averages, which were about equal to the results from MODCOMP^© with a coefficient of 40 percent but much lower than the results from MODULUS, which had a coefficient of variation of 65 percent.

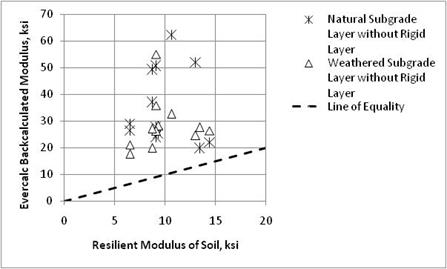
Figure 27. Graph. Comparison of backcalculated elastic moduli of unbound layers using EVERCALC^© and laboratory-derived resilient modulus.

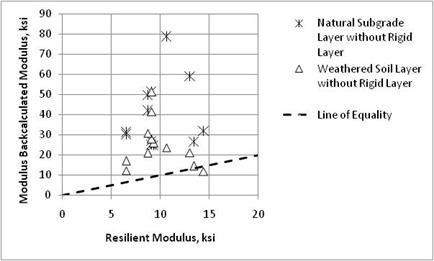
Figure 28. Graph. Comparison of backcalculated elastic moduli of unbound layers using MODULUS and laboratory-derived resilient modulus.

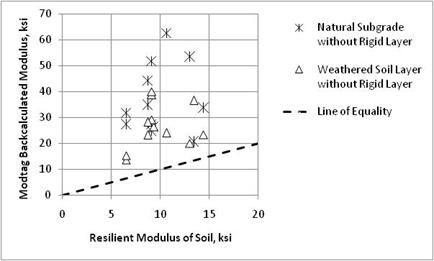
Figure 29. Graph. Comparison of backcalculated elastic moduli of unbound layers using MODTAG^© and laboratory-derived resilient modulus.

CASE STUDY Summary

Candidate programs were used to estimate elastic layer modulus values for the same deflection basins. Observations from the case studies were the same as those documented in the Smith study.⁽⁵³⁾ EVERCALC^© consistently resulted in lower error terms and a higher number of successful modulus determination when considering all deflection basins. When only considering those deflection basins that ran successfully, the MODCOMP^© program resulted in the lower RMSE values.

The results from the case studies suggest the use of multiple software packages for various pavement types. Thus, two software packages and one method were selected for use in the production runs for flexible and rigid pavements: EVERCALC^© and MODCOMP^© for flexible pavements and those two plus the best fit method for rigid pavements. EVERCALC^© was selected as the primary package, while MODCOMP^© was used to confirm discrepancies or anomalies identified by EVERCALC^©. Another reason for selecting MODCOMP^© is that EVERCALC^© is restricted to five layers, including a rigid layer if present, while MODCOMP^© can simulate up to seven layers.

¹ MODTAG^© includes various data subroutines for evaluating the deflection basin data and uses MODCOMP^© for the backcalculation process. MODTAG^© was used in the comparison of the programs within the first phase of the project. However, MODCOMP6^© was used for the production or batch runs under the second phase of the project.

² Some of the PCC elastic modulus values from the best fit unbonded condition exceeded 10 million psi, and these are not shown in the figure. These high elastic moduli resulted in a much higher standard deviation than for the EVERCALC^© method.