Long-Term Pavement Performance Program Determination of In-Place Elastic Layer Modulus: Backcalculation Methodology and Procedures

Chapter 4. Backcalculation Processs

One of the difficulties in backcalculation is that no unique solution or set of elastic layer moduli for a specific set of measured deflection basins is determined. More importantly, the quality of the results is heavily dependent on the knowledge and expertise of the user in setting up the problem. In other words, different users can obtain different results for the same set of deflection basins. This non-uniqueness of solutions has been a major deterrent for some agencies to take full advantage of backcalculation methods for routine rehabilitation design. Many agencies limit use of the deflection data to determine the subgrade elastic modulus. Thus, a key goal of this project was to automate the process and make it less dependent on the user so that others not directly involved in the development of the tools and procedures can recreate the results.

This chapter provides a general overview of the backcalculation process. In addition, it discusses the steps and decisions that were automated in setting up the problem and describes the tools written to simplify the backcalculation process while taking full advantage of the entire deflection basin data for rehabilitation design in accordance with the MEPDG.⁽¹⁾ The criteria used for determining whether the results are acceptable are also included in this chapter. The automated process is specific to LTPP and the data structure/tables included in the LTPP database. However, the steps and activities presented here can be used to improve the backcalculation of elastic layer moduli for individual rehabilitation projects.

Backcalculation Procedures and User Guide for Software Programs and Utility Tools includes a user’s guide for the automated backcalculation process as well as executing the utility and software tools for organizing the results included in the CPTs in the LTPP database.⁽⁵⁶⁾ This chapter summarizes the decisions for the pre-processing part as well as the generation the inputs for the backcalculation programs and a review of the results for acceptability.

Overview Of Process

Figure 30 shows a simplified flowchart of the major steps and decisions used in the backcalculation process.

Figure 30. Flowchart. Major steps and decisions in linear elastic backcalculation process.⁽⁴⁾

The following list explains the major steps and activities for each step:

1. Extract the following data needed for the backcalculation and interpretation of results:

• Deflection basin data and associated information (dates and times of testing, temperatures, etc.).
• Sensor location or offset distance.
• Pavement cross section (layer types and thicknesses).
• Maintenance and rehabilitation activities. The maintenance and rehabilitation history of the selected sections were used for establishing the layering of each section with time.
• Shoulder or boring information from the deeper samples. A macro was written to identify selected words on the boring logs to determine the depth to refusal or some hard layer as well as the depth to a saturated or wet layer.
• Information on the types and magnitudes of distress along the test section.
• Distress data measured over time, specifically, the distresses that affect the load-response behavior (cracking and distortion (rutting and faulting)).

2. Categorize test section and deflection basin data to identify anomalies and determine if there is an issue with the deflection basins. The important point of this step is to determine if the categories changed during different testing dates. If there appears to be a problem with the deflection basins within a specific date that is different from the others, these are marked and coded. Steps include the following:

• Execute the deflection basin and load-deflection response classification. All deflection basins were characterized by the same four categories established by Von Quintus and Simpson: type 1, type 2, type 3, and typical.⁽⁴⁾ The decision criteria for the categories are included in a flow chart in Backcalculation Procedures and User Guide for Software Programs and Utility Tools.⁽⁵⁶⁾
• Execute the Sensor Location Independent Check (SLIC) program within MODTAG^© to confirm or check any anomaly identified.

3. Determine structure or layering assumptions to be used as follows:

• Identify insensitive layers; assume the modulus of an insensitive layer or combine it with an adjacent layer.
• Combine similar and adjacent layers but separate significantly different and thick soil strata as well as thick aggregate layers.
• Identify layer anomalies and potential problem layers, such as sandwich sections, stiff soils above weaker or saturated soils, etc.
• Estimate depth to apparent rigid layer.
• Estimate depth to the water table.

4. Format deflection basin data into the requirements of the software package and set up preliminary trial runs. Most of the inputs are the same between the different programs, but the format for the deflection basin data is different. Steps are as follows:

• Execute trial computations.
• Compare the results with the allowable RMSE and acceptable modulus values for the layers and materials in question.
• Review adjacent layer modulus ratios between unbound layers to identify unrealistic or improbable conditions.
• Make any necessary adjustments to the layering assumptions.

5. Execute mass or batch backcalculation of deflection basin data for a specific site.

6. Extract and store results in summary tables from the backcalculation package (discussed further in chapter 5).

Backcalculation Programs

As discussed in chapter 3, two backcalculation programs and one method were used in step 5 and are described as follows:

• EVERCALC^© was the primary program used for the analyses and was used for all data and all pavement types in LTPP. The pre- and post-processing utility tools for the EVERCALC^© analyses were fully automated. The automation process included the generation of input files based on pavement simulation rules, the execution of EVERCALC^©, and post-processing the results.
• MODCOMP6.0^© was used as the auxiliary program to backcalculate results for those LTPP sections that did not yield acceptable results with EVERCALC^©. The MODCOMP^© analyses were semi-automated as an iterative approach, and the simulated backcalculation structure was selected on a case-by-case basis until the results converged within the selected criteria. A few test sections or portions of test sections did not converge to produce satisfactory results even after multiple efforts using EVERCALC^© and MODCOMP^©. Chapter 5 provides more information on the feedback reports and error flags to identify these sections as part of the post-processing process.
• The best fit method was used to analyze LTPP sections with a PCC surface to obtain the subgrade k-value and the elastic moduli of the PCC and base layers. The PCC and base modulus values were determined for two interface conditions—bonded and unbonded.

Prior to the execution of the backcalculation programs, the project team established the criteria for establishing a quantitative measure for categorizing the validity of the backcalculated modulus values. This was based on two parameters: the generated RMSE and the magnitude of the backcalculated modulus value for each layer depending on the layer type and layer category. The RMSE criterion was set at 3 percent (i.e., for the results to be valid, the RMSE needed to be at or below 3 percent). Also, the backcalculated modulus value for each layer had to fall within the acceptable or atypical range for each material type (see Backcalculation Procedures and User Guide for Software Programs and Utility Tools).⁽⁵⁶⁾ It was envisioned that all results would ultimately be categorized as follows and defined by the assigned ERROR_STATUS, which is a term used to identify the RMSE magnitude in a column within the LTPP backcalculated elastic layer moduli computed parameter table database:⁽⁵⁷⁾

• Accept: This includes basins for which the RMSE values were less than or equal to
  3 percent, and the backcalculated modulus results were within the specified acceptable range for each layer. The range specified for each layer depended on the layer type and layer category, which are discussed in Backcalculation Procedures and User Guide for Software Programs and Utility Tools.⁽⁵⁶⁾
• Atypical: This includes basins for which the RMSE values were less than 3 percent and the backcalculated modulus values exceeded the acceptable range but were within the atypical range as defined in Backcalculation Procedures and User Guide for Software Programs and Utility Tools.⁽⁵⁶⁾
• Error: This includes basins for which the RMSE values exceeded 3 percent and/or the backcalculated modulus values exceeded the atypical range defined in Backcalculation Procedures and User Guide for Software Programs and Utility Tools.⁽⁵⁶⁾

The error status for the best fit results was based on the modulus values of the PCC and the base layers for the bonded condition. Additionally, the RMSE4 value, which is the RMSE value determined from the measured and computed deflections for the four sensors used in the best fit analysis, was the basis for assigning the error status for the best fit method.

All programs were executed in a batch mode process on a state-by-state basis to handle the large volume of deflection basins in the LTPP database. Most of this chapter focuses on the decisions made in automating the process to determine inputs to the EVERCALC^© and MODCOMP^©programs. The best fit method provides unique solutions for PCC-surfaced pavement using a three-layered structure. Appendix A provides more detailed information on the computations and equations used to calculate the unique solutions from selected sensors within the deflection basin. Some revisions were made to the method that was originally developed during the first round of backcalculation sponsored by FHWA.⁽³⁾ Thus, appendix A focuses on describing the mathematics used to calculate the elastic modulus and k-value of the PCC-surfaced test sections.

The EVERCALC^© and MODCOMP^© analyses were performed in four main analysis phases. Each phase progressively identified and filtered out those cases with poor quality results and made appropriate adjustments to the analysis parameters to improve the convergence in the subsequent phase. The first phase included all LTPP data, while the second used a subset from the first phase. The third and fourth analysis phases, if required, used a subset from the second phase. The four phases include the following:

1. The first analysis phase included EVERCALC^© analysis for all LTPP sections using material parameters selected to represent typical ranges of inputs values for each material/layer type. Results from the first phase analyses were examined to classify them into the accept, atypical, or error categories described previously.
2. The second analysis phase included an expanded modulus range for the analyses of the LTPP test sections or test days with more than 25 percent atypical (i.e., invalid) results in the first phase analysis (converged to one of the boundary limits with RMSE values less than 3 percent) and RMSE values for the other stations being less than 5 percent. If the majority of the results converged to one of the boundary modulus values and resulted in high RMSE values (greater than 5 percent) defined as errors, the results and pavement simulation structure were manually reviewed based on compensating error effects (two layers resulted in hitting upper and lower modulus boundary limits) and the potential for layer anomalies.
3. The third analysis phase included test days with erroneous results at the end of the second phase and was performed using MODCOMP^©. Results from the second phase were evaluated between multiple test days for inconsistency in results. The focus of the third phase was performing a manual review of the results and making appropriate revisions of the simulated structure to obtain acceptable results. The pavement structure simulation was revised based on whether the second phase results showed an invalid layer modulus, whether there were compensating errors (defined in chapter 5), whether extensive distresses were present, and whether the potential for layer anomalies could exist.
4. In some cases, a fourth analysis phase analysis was performed using MODCOMP^© and a revised pavement simulation structure based on the results from the second and third analysis phases. If unacceptable results were obtained after the fourth phase, no additional analyses were completed.

LTPP Data

The deflection data were extracted from LTPP Standard Data Release (SDR) 27.0 (released in 2013) and included specific data from all LTPP test sections for all days of deflection basin testing. The data needed for the backcalculation of layer modulus values were grouped into
two categories: direct and indirect. Table 5 lists the LTPP data tables from which the direct and indirect data were extracted for the pre-processing tools to establish the inputs and the post-processing tools to evaluate the final results.

The direct data were from tables that needed to establish the inputs for the backcalculation and forward calculation of layer moduli, and the indirect data were from tables that needed to evaluate the results from the backcalculation process. The direct data elements were extracted from the LTPP database for all test sections on an experiment basis. The indirect data elements were extracted for those test sections that had an appreciable number of results that were considered unacceptable in order to identify potential reasons for the unacceptable or poor results.

Note: Other data elements were extracted and used indirectly from the LTPP database. The ones listed in this table are more commonly used.

Presence of Bedrock Layer

In the first and second phases of the analyses, all sections were analyzed using the following two assumptions:

• Without a rigid layer: All cases were analyzed using the EVERCALC^© program interface. The execution of EVERCALC^© using this assumption was automated, thereby eliminating the need for manual intervention to complete the analyses.
• With a rigid layer: All these cases were analyzed by running EVERCALC^© using the backcalculation.exe application from the MS-DOS prompt. In many cases, the depth to a rigid layer was calculated, but the RMSE was high, exceeding its upper limit.

The automation process compared the RMSE and range of backcalculated elastic moduli resulting from the pavement simulation with and without a rigid layer. Whichever simulation resulted in the lower RMSE was used for further analyses. In many cases, the RMSEs were significantly different.

The presence of a rigid layer was also verified independently in the second and third analysis phases. The depth to a hard layer was included in the automation process by identifying selected words on the deeper borings or shoulder probes. Some of the words included in the search were refusal, hard layer, hard pan, rock, and limestone.

The best fit procedure did not require a different treatment of the data for sections with or without a stiff layer. The k-value was assumed to reflect, or at least account for, the presence of a bedrock layer in the backcalculation structure.

Presence of Ground Water or Wet Layer

It has been the authors’ experience that separating dry and wet or saturated layers improves the accuracy of the solution. Thus, the same tool to determine the depth to a hard layer was used to search the shoulder probes for wet layers. The words used in the search were “water,” “wet,” “soft,” and “saturated.” This depth was used to initially separate the weathered subgrade layer from the natural subgrade.

Pre-Processing and Computational Tools

The analyses were performed in a systematic manner, as documented in Backcalculation Procedures and User Guide for Software Programs and Utility Tools.⁽⁵⁶⁾ In keeping with the requirements outlined by LTPP, the analyses were automated to minimize manual errors and to enable an independent user the ability to reproduce the results. In addition, the automation process was designed to enable users to generate results for additional data collected by LTPP in the future. The analyses utilized raw data in Microsoft Access^® format from the LTPP database as the starting point to generate the backcalculation results. The results were merged back into Microsoft Access^® tables with common reference fields with the original deflection tables, as explained in the description of the data schema provided in Schema for the Computed Parameters Table.⁽⁵⁷⁾ Therefore, Microsoft Access^®-based macros, Microsoft Windows^®-based utilities, and user interfaces were developed to do the following:

• Perform general data validity checks.
• Use the original LTPP tables to merge deflection, sensor spacing, and temperature data.
• Establish data flags to filter out problem basins (i.e., those with non-decreasing deflections, missing deflection data, or missing sensor spacing data). Missing temperature data were flagged but not discarded for backcalculation.
• Process pavement layer information from raw data in LTPP tables to develop backcalculation structure suitable for use in the EVERCALC^© program. This involved combining pavement layers so as to reduce the pavement structure to an equivalent backcalculation layer structure meeting EVERCALC^© requirements.
• Assign reasonable seed modulus values and range of modulus values for use in the backcalculation process.
• Generate the input files in the format necessary for use in the EVERCALC^© program.
• Generate input files in the format necessary for use in the MODCOMP^© analyses. Because the MODCOMP^© analyses followed EVERCALC^©, the input files for MODCOMP^© were created by modifying the EVERCALC^© input files.
• Generate the input files in the format necessary for the best fit analyses program. These files were created directly from the Microsoft Access^® data tables and were independent of the EVERCALC^© or MODCOMP^© analyses.
• Execute the EVERCALC^© analyses in a batch mode.
• Execute the MODCOMP^© analyses in a batch mode.
• Execute the best fit analyses in a batch mode.
• Calculate the load transfer efficiency (LTE) across the transverse and longitudinal joints in JPCP sections and across transverse cracks in CRCP sections.
• Read output data files, merge results, and compute summary tables for inclusion in LTPP results database.

The macros were developed in Microsoft Access^® primarily because the raw data resided in Microsoft Access^® tables. The macros were used to perform the preliminary data checks and to create supplementary data tables. Supplementary data are all data other than the raw FWD deflection data that are necessary to perform the backcalculation analyses, including sensor spacing, temperature data, backcalculation layer structure and layer thicknesses, layer material information including specified ranges for EVERCALC^© analysis, and beta factors for the best fit analysis methods.

A standalone software program, Back Calculator, was developed for this current study for bulk processing and filtering the deflection data, for executing the EVERCALC^© program and the best fit method, and for processing the backcalculation results. Back Calculator is discussed in Backcalculation Procedures and User Guide for Software Programs and Utility Tools.⁽⁵⁶⁾ MODCOMP^© analyses were not included in this program because only a limited number of sections were analyzed using MODCOMP^©. MODCOMP^© analyses were performed in a batch mode by executing the application file from an MS-DOS prompt.

Pre-Processing Deflection Data

The pre-processing tools for the deflection data were used to convert deflection basin data from the format in which they were collected to the format required for input to the backcalculation program as well as to identify deflection data anomalies that cause the program to generate unrealistic solutions and establish the pavement layering simulation.

Two parameters were checked in terms of pre-processing the deflection basin data: the type of deflection basins (typical and types I, II, or III) and type of structure (deflection softening, elastic, or deflection hardening). Von Quintus and Simpson and Von Quintus and Killingsworth defined and used these parameters during the first round of backcalculation of layer moduli as well as in other local calibration studies.^(4,45) Deflection basins identified along a test section inconsistent with elastic layer theory were flagged.

The deflection basin and load-response behavior categories can also be used to guide the initial pavement layering simulation. For example, sites with a high percentage of type II deflection basins usually indicate some stiff layer close to the surface but not at the surface or some discontinuity at the surface varying from cracks to debonding. Different pre-processing activities related to the deflection data include the following:

• Pre-processing of deflection data was performed to determine the deflection basin and load-response categories, as well as identify sensor data issues using SLIC (part of the MODTAG^© program for evaluating the deflection basin data). The decision criteria for categorizing each test section and deflection basin are documented in the Von Quintus and Simpson report.⁽⁴⁾
• An apparent rigid or stiff layer was estimated along each test section in accordance with the procedure identified by EVERCALC^© and MODCOMP^©. The depth to an apparent rigid layer can be highly variable along a test section as well as between test days.
• Deflection basin data were reviewed to identify changes in the categories over time, which could indicate a seasonal water table depth, increased damage, and/or occurrence of distress (cracking and distortion) or debonding between adjacent layers.

The representative thickness of the structural layers of an LTPP test section was determined to be the average thickness of that layer. For most of the LTPP test sections, layer thicknesses were only measured at the beginning and end of the section. In a few cases, the layer thickness and material types varied from one end of the section to the other. Thickness variations along a site can have a detrimental effect on trying to determine acceptable layer modulus values for that site.

The measured deflections were used to subdivide the sections into two parts when the layer thickness from the approach and leave ends of the section varied significantly. There were sites with an abrupt change in the measured deflections from one end to the other, and other sites where the measured deflections continually decreased or increased from one end to the other. LTPP sponsored a study using GPR data to estimate the variation of layer thickness throughout some of the test sections. These GPR data, when available, were used to make a decision on subdividing an individual section.

The process compared the layer thickness measured on the leave and approach ends of each test section. The initial criteria used for comparison was 0.5 inch for PCC and HMA layers and 1 inch for the unbound base and treated subgrade (TS) layers. If no significant difference in layer thickness was measured, LTPP materials data table TST_L05B within the LTPP materials database was used to determine the representative layer type and thickness at the site. For those sites with large deviations in layer thickness, the layer thicknesses determined from the GPR data were used to determine if the test section should be subdivided. If GPR data were unavailable, the deflection data were used to decide whether the test section should be subdivided into multiple test sections for backcalculating elastic modulus values.

Pavement Simulation Rules

The number of layers and individual layer thickness are critical parameters for backcalculating the elastic modulus of structural layers (i.e., layers that have a significant impact on the deflection basin with reasonable changes or variation in modulus). Getting a reasonable starting pavement simulation for the measured deflection basin is probably the most important activity in the backcalculation process, and as such, was included as an automated feature in the pre-processing tools to remove subjectivity.

Most backcalculation software packages limit the number of layers that can be backcalculated to a maximum of three and five, but that number depends on the number of sensors and their spacing. The first and second phases of the backcalculation process were limited to five layers to accommodate the features of the selected backcalculation program. The third and fourth analysis phases explored the option of using up to seven layers, including any known layer modulus or insensitive layer. However, the results that were acceptable included no more than five layers. Therefore, under this project no more than five layers were backcalculated.

The rules of simulation reported in the MEPDG were used to set up the pavement structure for each LTPP test section.⁽¹⁾ Setting up the initial pavement layering simulation is straightforward, but there are factors that complicate the process. For example, layer thicknesses are not known at every deflection point, and some subsurface layer conditions can be overlooked or not adequately identified throughout the test section. The following lists provide some general rules of simulation for creating the pavement structure used in backcalculating elastic layered modulus for each of the structural layers. Many of these rules are discussed in other areas of the report, but they are repeated here for the convenience of the reader.

General notes include the following:

• It is optimal to start with the fewest number of layers possible and estimate the depth to an apparent rigid or stiff layer for each drop height along the test section prior to program execution.
• Thin non-structural layers should be combined with adjacent like layers. Thin is defined as less than 2 inches or less than half the thickness of the layer above the layer in question. As an example, an HMA open-graded friction course should be combined with the supporting HMA layer. In many cases, thin layers are defined as insensitive layers.
• The moduli for the insensitive layers were assumed using typical values included and reported in the MEPDG, or the layer was combined with an adjacent “like” layer.⁽¹⁾ As noted above, an insensitive layer is defined as one that has little to no impact on the measured deflection basin.
• GPR data were used to estimate the change in thickness and subsurface conditions along the test section. Where available, GPR data were reviewed to estimate significant changes along the test section from what is recorded in the L05B table (layer thickness, subsurface feature, etc.). If the GPR data suggested variable layer thickness between the ends of the section, a decision was made on whether to subdivide the section into two parts. If a substantial difference in surface layer thickness was found between the leave and approach ends and GPR data were unavailable, deflection data were used to determine the location of the transition. If an abrupt change was identified via the deflection basin, the section was subdivided into two subsections.
• Similar or like materials of adjacent layers should be combined into one layer. Like is defined as materials or layers with the same AASHTO classification exhibiting similar laboratory-measured modulus values and the same stress-sensitivity and physical properties. Like layers were combined in setting up the structure at a particular site. This is one of the reasons for extracting the layer material properties for use in this study.
• The lower layers should be combined first, and the upper pavement layers should be treated in more detail, if possible. The discussion and guidance that follows, however, starts with the foundation layers and proceeds up to the surface layers.

Subgrade layer notes include the following

• Boring logs and shoulder probes should be reviewed to determine the foundation soils and the vertical strata and their condition.
• At the beginning, the subgrade or foundation soils should be divided into two layers, especially when bedrock and other hard soils are not encountered. The lower layer represents the natural soil, while the upper layer represents the compacted soils just beneath the pavement materials. This layer is considered to be the weathered soil layer.
• Bedrock and other hard soils (such as hard pan, shale, sandstone, etc.) believed to be more than about 20 ft below the surface usually have an insignificant effect on the calculated pavement responses for predicting various distresses. In some cases, however, better results were obtained if that hard layer was simulated within 600 inches to the surface.
• Depth to a water table or wet layer is important for both structural evaluation and backcalculation of layer modulus. It is optimal to stratify the subgrade at the depth of the water table because of the different layer response to load. The water table can vary by season, so the layering at a site can be different within different seasons.
• Geo-synthetic fabrics and other materials are not simulated by themselves in the structural response program. However, these types of reinforcing fabrics can result in a higher modulus of the layer in which they are placed. Filter fabrics used for drainage purposes between a fine-grained soil and aggregate base material are not simulated in the pavement structure and usually have no impact on the structural response of the pavement.

Unbound aggregate material notes include the following:

• In most cases, the number of unbound granular base (GB) and subbase layers should not exceed two, especially when one of those layers is thick (more than 18 inches in thickness). Sand and other soil-aggregate materials should be simulated separately from crushed stone or crushed aggregate base materials.
• If thick, unbound aggregate or select materials (i.e., exceeding 18 inches) are used, this layer can be treated as the upper subgrade layer. Thick granular layers are typically used in northern climates as non-frost susceptible materials. When these layers are treated as the upper subgrade, then only one subgrade layer is needed.
• If a thin aggregate base layer is used between two thick unbound materials, the thin layer should be combined with the weaker or lower layer. For example, a 6-inch sand subbase layer placed between an A-1-b AASHTO classified subgrade soil (SS) and crushed stone base can be combined with the upper subgrade layer.
• When similar aggregate base and subbase materials are used, those materials can be combined into one layer.

Treated and stabilized material notes include the following:

• ATB layers, sometimes referred to as “blackbase,” should be treated as separate layers and not combined with dense-graded HMA base mixtures. Typically, these are crushed stone base materials that have a small amount of asphalt and/or emulsion that can be produced at a plant or mixed in place. However, ATB materials that are designed using the gyratory compactor or other compaction device and produced through a production facility can be treated as an HMA base material and combined with other dense-graded HMA layers.
• Cement-treated and other pozzolanic stabilized materials that are used as a base layer for structural support should be treated as a separate layer. In some cases, a small portion of cement, lime, or fly ash may be added to GB materials to improve the strength or lower the plasticity index of those materials for constructability issues. These materials should still be considered as a separate layer.
• Lime and lime-fly ash stabilized SSs should be treated as a separate layer, if possible. In some cases, a small amount of lime or lime-fly ash is added to soils in the upper subgrade to lower the plasticity index and from a constructability standpoint. For these cases, the lime or lime-fly ash stabilized soil should be combined with the upper subgrade layer.

Drainage layers/material notes indicate that permeable ATB drainage layers should be treated as separate layers and not combined with dense-graded HMA layers or ATB layers, if possible.

HMA mixture notes include the following:

• Similar HMA materials should be combined into one layer. For example, an HMA wearing surface or mix and an HMA binder layer can be combined into one layer without affecting the accuracy of the predictions.
• Thin HMA layers can be combined with an adjacent HMA layer. As noted earlier, thin is defined as less than 2 inches in thickness. Thin HMA leveling courses, or for the condition when the thickness of the leveling course is highly variable along the roadway, can be combined with the other HMA layers or ignored without affecting the overall accuracy of the results.
• The number of HMA layers should not exceed two, if at all possible. All layers that are dense-graded HMA mixtures should initially be combined.

Defining Acceptable Elastic Layer Modulus Values

Two parameters were used to judge the acceptability of the backcalculated values: (1) the error or RMSE between the measured and calculated deflection basins and (2) a comparison of the backcalculated values to the range of typical material specific values. A third factor was used (normality test for the results for a day’s test) but only for evaluating the acceptability of the results.

Error Between Predicted and Measured Deflection Basins

All of the measurement points that have excessive error terms were flagged and not used in determining the statistics (means and standard deviation) for the test section and day of testing. Excessive is defined as an RMSE value greater than 3 percent. Deflection basins with RMSE values greater than 3 percent were included in the point-by-point CPTs (see Schema for the Computed Parameters Table) but excluded from the CPTs in determining the average of the in-place elastic moduli for each test section and test date.⁽⁵⁷⁾ Chapter 5 provides a summary of the CPTs for the backcalculation of elastic layer moduli.

Range of Calculated Modulus Values

The other criterion used in judging the acceptance of the results is the range of typical modulus values. The range of modulus values for typical materials and soils was determined to be consistent with values reported in the MEPDG.⁽¹⁾ Table 6 provides the range of typical modulus values included in the MEPDG.⁽¹⁾ The table also includes the range of values used for judging the reasonableness of the backcalculated layered elastic modulus values. Note that the table does not list all materials that are included in the LTPP program. It is a partial list to show examples of the typical range in material moduli.

N/A = Not applicable.
^aThe range of values for the backcalculation process are preliminary and depend on the physical properties and condition of the layers documented in the LTPP database or extracted from other reports and construction records.

During the first round of backcalculation values, some of the results were believed to be unacceptable because the backcalculated values fell outside the range of typical values. Although this factor was used to judge the results, the results are not necessarily unacceptable simply because the values fall outside a perceived range of values. Some of the results that were believed to be unacceptable from the first round have been found to be reasonable as a result of forensic and other investigations completed at specific LTPP test sections.

For example, some of the elastic modulus values for unbound aggregate base layers in Arizona were found to be greater than 100 ksi, which is extremely high. It was later found, however, that these unbound aggregate base layers had very low water content, and the fines were binding the base particles together so the aggregate layers were responding as bound layers. Some of the crushed limestone aggregates used in central Texas exhibited the same behavior when dry.

Normality Test Using Jarque-Bera Test Statistic

Another factor included in the automated process for evaluating the acceptability of the results was to determine if the calculated elastic layer moduli are characteristic of a normal distribution. Just about all volumetric and structural properties exhibit a normal distribution unless there is some type of bias that is created during construction or a boundary condition. Thus, results from a single test day were evaluated to determine if those results exhibited a normal distribution.

The verification for normal distribution was performed using the Jarque-Bera test statistic. For given data, x₁, x₂, …, x_n, the statistical terms shown in table 7 are calculated based on the normality test class.

Table 7. Statistical parameters calculated for normality check.

Statistic terms	Statistic Symbol	Functions from Code
Sample mean		Mean
Second central moment (variance)		Variance
Third central moment (skewness)	S	Skewness
Fourth central moment (kurtosis)	K	Kurtosis
Jarque-Bera test statistic	JB	JarqueBeraTestStatistic

Figure 31 shows the formula for the skewness factor, figure 32 shows the equation for kurtosis factor, and figure 33 shows the equation for the Jarque-Bera statistic.

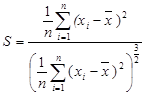
Figure 31. Equation. Skewness factor.

Where:

S = Skewness factor.

n = Number of data points in the sample.

i = Individual data point within the sample.

x_i = Data value within the sample.
= Sample mean.

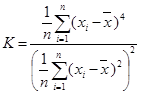
Figure 32. Equation. Kurtosis factor.

Where K = Kurtosis factor.

Figure 33. Equation. Jarque-Bera statistic used for verifying normality in data.

Where JB = Jarque-Bera statistic.

For a dataset that is normally distributed, it is expected that S and K both equal zero.

JB asymptotically has a chi-squared distribution with 2 degrees of freedom. The critical value is determined using table 8. Hence, at a significance level of 5 percent and 2 degrees of freedom, the critical value is 5.99 (shown in bold in the table). Therefore, if JB is greater than 5.99, S and excess K tend to deviate from zero, which does not imply a normal distribution. JB values less than 5.99 indicate a normal distribution.

Note: Bolding indicates the critical value.