Long-Term Pavement Performance Program Determination of In-Place Elastic Layer Modulus: Backcalculation Methodology and Procedures

Appendix A: Best Fit Method—Calculating PCC Elastic Layer Moduli

The best fit method proposed previously for the backcalculation of LTPP rigid pavement deflection data was adopted in this project.⁽³⁾ All concrete-surfaced LTPP sections were analyzed using the best fit procedure, which involves the backcalculation of a two-layered (PCC and base) slab-on-grade.^(28,58,59) The procedure was recommended after the completion of the case studies evaluation for the following reasons:

• The procedure is founded on sound mechanistic concepts. It is based on Westergaard’s solution for an interior loading condition of a plate resting on a dense-liquid foundation. The plate is assumed to behave as a linear elastic, homogeneous, and isotropic material.
• The results were found to be reasonable and generally producing reasonable RMSE values for sections included in the case studies to demonstrate and compare the use of the candidate programs.
• The procedure can be used for any sensor configuration and provides the best fit between the measured deflection and the calculated deflections.
• The procedure is consistent with the MEPDG rigid pavement analysis in aspects relating to the reduction of the pavement layer structure to a two-layered PCC slab-base structure.⁽¹⁾ Within the framework of the MEPDG analysis, the two-layered structure is subsequently simulated as an effective slab-on-grade problem, with the slab assigned an effective structural capacity determined by the thicknesses of the slab and base and the contact friction between them (see figure 81). The best fit method analyzes the structure as a slab-on-grade problem to determine the composite modulus of the effective slab. Further, depending on the slab-base bond condition assumption, appropriate methods are used to apportion the stiffness of the effective slab between the individual slab and base.
• The results are generated rapidly, making it suitable for processing the large datasets used in this project. Each deflection basin is analyzed in a fraction of a second.

The best fit approach may be considered as one that determines the stiffness of a fictitious effective slab which deforms in a manner identical to the actual pavement under the applied FWD loads. Therefore, the procedure attempts to match the deflection of the simulated effective slab with the measured deflection from the FWD testing. The simulation uses the same level of load as the FWD test and positions the load in the slab interior comparable to the J1 point location in the LTPP database.

E_PCC = Elastic modulus of the PCC layer.

E_base = Elastic modulus of the base layer.

h_PCC = Thickness of the PCC layer.

H_base = Thickness of the base layer.

H_eff = Effective thickness of the pavement.

Figure 81. Illustration. Transformation of design structure to effective structure used by the neural networks to compute mechanistic responses.

In the figure, the effective thickness parameter derived from section transformation in step 2 changes with the interface bond condition (i.e., h_eff) is smaller for the unbond condition. Additionally, the JPCP faulting model uses an unbonded interface for the calculation of corner deflections, while CRCP is always modeled as an unbonded section.

The optimization procedure solves for the specific combination of the coefficient of subgrade reaction and the radius of relative stiffness, which result in slab deflections closest to the measured deflections at each sensor. The procedure allows for the use of weighting factors for the error at each sensor, and the convergence criterion is the minimization of the sum of the mean squared errors from each sensor, with the error weighted by a pre-defined factor for each sensor. Therefore, the solution is determined by the minimization of the error function expressed as follows:

Figure 82. Equation. Error function definition for best fit procedure.

Where:

F = Error function dependent on the elastic modulus and coefficient of subgrade reaction.

E = Elastic modulus.

k = Coefficient of subgrade reaction.

n = Number of increments.

α_i = Weighting factor.

w(r_i) = Calculated deflection.

W_i = Measured deflection.

The deflection at any point at a radial distance measured from the center of a circular load plate distributing uniform pressure may be expressed as a function of r as follows:

Figure 83. Equation. Calculated deflection.

Where:

r = Radial distance.
p = Pressure.
f = Function.
l = Relative stiffness.

Where f(r) is a function of two dimensionless parameters, the radius of the load plate normalized to the radius of relative stiffness, and the radial distance of the sensor normalized to the radius of relative stiffness. The pressure p is the uniform pressure under the applied load P, calculated as P/πa², where a is the loaded area under the loading plate.

The radius of relative stiffness and the subgrade k-value define the flexural rigidity of the effective slab. Most commonly, the radius of relative stiffness is expressed as a function of the effective plate thickness, h, elastic modulus of the effective plate, E, Poisson’s ratio, μ, and the k-value as follows:

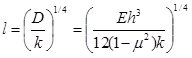
Figure 84. Equation. Radius of relative stiffness.

Where D = Stiffness of the PCC slab.

The error function in figure 82 can be rewritten using figure 83 as follows:

Figure 85. Equation. Error function in alternate form.

The best fit procedure satisfies the two conditions shown in figure 86 and figure 87 as follows:

Figure 86. Equation. Partial derivative of F with respect to k.

Figure 87. Equation. Partial derivative of F with respect to l.

The substitution of the error function in figure 85 in the conditions represented by figure 86 and figure 87 yields the equations to solve for k and l, as shown in figure 88 and figure 89.

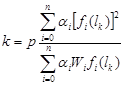
Figure 88. Equation. k-value.

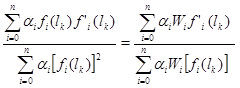
Figure 89. Equation. Radius of relative stiffness.

The computational effort involved in solving the equation in figure 89 forms the major component of the best fit procedure. The k and l values determined from the equations in figure 88 and figure 89 are substituted into the equation in figure 84 to determine the modulus of the plate or the effective slab.

Estimation of Base Layer Modulus in Best Fit Procedure

The modulus backcalculated for the effective slab using the best fit procedure is subdivided between the slab and the base, which are assumed to provide a composite section in the calculated deflections. The effective contribution of the base layer in the overall stiffness of the composite section depends on two factors: the relative stiffness of the materials itself and the bond condition at the slab base interface.

To estimate the relative stiffness of the slab and the base materials, an additional parameter is introduced to quantify the modular ratio of the slab and base. The modular ratio, β, is defined as follows (where the asterisk represents an adjustment to the modular ratio):

Figure 90. Equation. Modular ratio.

Where:

E_Base = Base modulus.

E_PCC = PCC modulus.

The β* values used in the analyses were based on the LTPP material codes for the base layer and were borrowed from Khazanovich et al. (see table 17).⁽³⁾ Some material codes were assigned β* values under the current study and have been identified in the table. The selected values are based on β* values previously assigned for similar materials. In addition, for PCC layers overlaid using an unbonded PCC overlay, assuming the layer has undergone a fair level of damage, the stiffness was considered to be lower than a concrete slab in good condition ( β* = 1) but higher than an AC layer ( β* = 10). Therefore, a β* value of 5 was assigned for PCC layers that have an unbonded overlay according to the TST_L05B layer structure. Also, a material code of 1000 was assigned within the best fit software code to identify PCC layers with unbonded overlay.

*Represents material codes for which the modular ratios were established under this study.

^#Represents a material code assigned in the software program for all PCC layers that have an unbonded overlay.

The best fit procedure considers two distinct cases for the bond condition at the interface between the upper (PCC) and lower (base) slabs: unbonded slab-base interface and fully bonded slab-base interface. Intermediate levels of interface bond are not analyzed.

In the case of unbonded PCC-base condition, flexural stiffness of the effective slab can be presented as follows:

Figure 91. Equation. Flexural stiffness.

Where:

D_e = Flexural stiffness of the effective slab.

D_PCC = Flexural stiffness of the PCC.

D_Base = Flexural stiffness of the base.

For the unbonded conditions, PCC and base moduli are defined as follows:

Figure 92. Equation. Slab modulus from effective modulus for unbonded condition.

Where:

E_PCC =Elastic modulus of the PCC slab.

h_PCC = PCC thickness.

h_Base = Base thickness.

E_e = Effective modulus from best fit backcalculation.

Figure 93. Equation. Base modulus from effective modulus for unbonded condition.

For the case of the bonded base condition, the flexural stiffness of the effective slabs is derived using the parallel axis theorem. The PCC and base moduli are defined as follows, where x is the depth of the parallel axis from the surface as defined in figure 96 :

Figure 94. Equation. Sab modulus from effective modulus for bonded condition.

Figure 95. Equation. Base modulus for bonded condition.

Figure 96. Equation. Depth of the parallel axis from the surface.

Defining the Base Layer in the Pavement Structure

The project team developed procedures to identify layers in the pavement structure that could be treated as the base layer in the best fit analysis. Table 18 lists the layers below the PCC slab that were included in the base layer for different layer structures. The selection of the base layer was based on the following general rules:

• If the layer immediately beneath the PCC layer was an unbound GB layer with all layers below the GB layer of lower stiffness based on material type, the GB layer beneath the PCC layer was considered as the base layer.
• If the layer immediately beneath the PCC layer was a stabilized base layer with all layers below the stabilized base layer of lower stiffness based on material type, the stabilized base layer beneath the PCC layer was considered as the base layer.
• If the layer structure presented a stiffer layer below the layer immediately underneath the PCC slab, appropriate layers were combined to represent the base layer based on engineering judgment and as shown in table 18.
• If a TS layer was present, it was not combined into the base layer. Rather, the effect of the TS layer was apparent in the computed k-value of the subgrade.
• For unbonded overlay sections, the layers between the overlay up to and including the existing slab were included in the base layer.
• For bonded overlays, the existing slab and the overlay were combined into the surface layer. The layer immediately underneath the existing slab was used as the base layer.

GS = granular subbase.

TB = Treated base.

In the case of more than one layer between the PCC and subgrade, all base layers were combined into one layer. Using parallel axis theorem and defining the equivalent base thickness, h_eq, as the sum of the base layers thicknesses, it was possible to calculate the equivalent base modular ratio, β_eq. β_eq calculations for a structure with up to five layers combined into the base layer is further described.

If h_i is the thickness of the i^th base layers and β_i is the modular ratio of the i^th layer (from table 17), then for the case of five base layers, the equivalent base modular ratio can be calculated as follows:

Figure 97. Equation. Equivalent beta when multiple layers are combined into the base.

Where:

Expri = A model parameter defined in figure 99 and figure 100.

The variables in figure 97 are defined as shown in figure 98 through figure 103.

Figure 98. Equation. Equivalent thickness.

Figure 99. Equation. Expr1.

Figure 100. Equation. Expr2.

Figure 101. Equation. Depth of parallel axis from the surface when multiple layers are combined into the base.

Figure 102. Equation. Expr3.

Figure 103. Equation. Expr4.

Note that in these equations, the β values are the inverse of the β* listed in table 17. The β_eqvalue calculated in figure 97 provides the combined effective multilayer β value used in figure 89 to calculate the modulus of the effective base layer.