Using Multi-Objective Optimization to Enhance Calibration of Performance Models in the Mechanistic-Empirical Pavement Design Guide

CHAPTER 2. REVIEW OF LITERATURE ON CALIBRATING THE MECHANISTIC–EMPIRICAL PAVEMENT PERFORMANCE MODELS

INTRODUCTION

The first step in the proposed research study was a comprehensive literature review regarding calibration of the pavement performance models in the AASHTOWare® Pavement ME Design software. The literature review also included multi-objective model calibration studies in research areas other than pavement engineering. The major objective of this literature review was to identify important sources of information for model calibration and to formulate corresponding objective functions. The review also enabled researchers to base their selection of range and precision of possible calibration factors on previous calibration studies.

Results of previous calibration efforts indicated little to no problem in calibration of thermal (transverse) cracking and smoothness prediction models. Therefore, the existing single-objective calibration procedure seems to be sufficient for these two models.⁽³⁾ There seem to be difficulties in calibration of the longitudinal cracking model associated with the lack of fit of the global model.⁽⁵⁾ These difficulties require reconsideration of the formulation for the longitudinal cracking model, and therefore, this model is not considered for this research project.

The permanent deformation model has been reported to consistently overpredict measured pavement rutting. On the other hand, the fatigue cracking model has been reported to underpredict actual pavement distress in most studies. A more sophisticated calibration procedure could address these consistent deviations of model predictions from measured pavement performance. This research project was therefore originally focused on local calibration of prediction models for rutting and fatigue cracking in flexible pavements. Hence, the following literature review includes information regarding both models. However, due to limitations in the resources and schedule of this project, only the permanent deformation models were considered to demonstrate the proof of concept for multi-objective calibration.

MECHANISTIC–EMPIRICAL PAVEMENT PERFORMANCE MODELS

The amount of total permanent deformation in flexible pavements is calculated as the sum of plastic deformations in each of the hot-mix asphalt (HMA), base, and subgrade layers. The model for predicting rutting (permanent deformation) in HMA layers (inches)^[1] of flexible pavements has the form of equation 1:⁽¹⁾

     (1)

Where:

Δ_p = predicted rutting (inches).
h_HMA= thickness of the HMA layer (inches).
ε_p= plastic strain in the layer (inch/inch).
ε_r= resilient (recoverable) strain in the layer (inch/inch).
T = layer temperature.
N = number of load repetitions.
k₁, k₂, k₃ = global field calibration parameters (from NCHRP 1-40D Recalibration, k₁ = –3.35412, k₂ = 1.5606, k₃ = 0.4791).
β_r1, β_r2, β_r3 = local or mixture field calibration factors; these factors were all set to 1.0 for the global calibration.
k_z= depth confinement factor, which is calculated through equation 2:

     (2)

Where:

D = depth below the surface
C₁ and C₂ = coefficients to calculate the depth confinement factor; these coefficients are calculated according to equations 3 and 4:

     (3)

     (4)

The model for predicting rutting in unbound (base, subbase, and subgrade soil) layers (inches) of flexible pavements has the form of equation 5:⁽¹⁾

     (5)

Where:

h_soil = thickness of the unbound layer/sublayer (inches).
k₁ = global calibration coefficient; k₁ = 2.03 for granular materials, and k₁ = 1.35 for fine-grained materials.
β_s1 = local calibration factor; this factor was set to 1.0 for the global calibration; it is also called β_GB for unbound base layers and β_SG for subgrade layers.
ε_v = average vertical resilient or elastic strain in the layer (inch/inch) calculated by the structural response model.
ε₀ = strain intercept (inch/inch) determined from laboratory repeated-load permanent deformation tests.
ε_r = resilient (recoverable) strain (inch/inch) imposed in laboratory test to obtain material properties.
= strain ratio that is calculated using equation 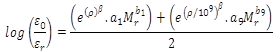6:

     (6)

β and ρ are material properties that are calculated according to equations 7 and 8:

     (7)

     (8)

Where W_c is water content (%) that is calculated using equation 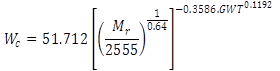9:

     (9)

Where:

GWT = depth of ground water table (ft).
C₀ = factor depending on the material resilient modulus and is calculated through equation 10:

     (10)

Where:

M_r = resilient modulus of the unbound layer/sublayer (psi).
a₁, a₉, b₁, b₉ = regression constants; a₁ = 0.15, a₉ = 20.0, b₁ = 0.0, and b₉ = 0.0.

The prediction model for fatigue (bottom–up or alligator) cracking (percent of total lane area) in flexible pavements has the form of equation 1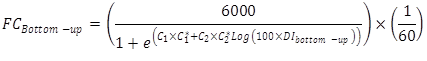1:⁽¹⁾

     (11)

Where:

FC_Bottom–up = bottom–up alligator cracking.
C^*₁ and C^*₂ are coefficients that can be calculated using equations 12 and 13:

     (12)

     (13)

Where

h_HMA = total HMA thickness.
DI_bottom–up = damage index that is calculated using equation 14:

     (14)

Where:

∆DI = incremental damage index.
N = actual number of axle load applications within a specific period.
j = axle load interval.
m = axle load type (single, tandem, tridem, quad, or special axle configuration).
l = truck type using the truck classification groups included in the MEPDG.
p = month.
T = median temperature for the five temperature intervals used to subdivide each month.
N_{f – HMA} = allowable number of axle load applications for a flexible pavement to fatigue cracking, and it is calculated using equation 15:

     (15)

Where:

ε_t = tensile strain at the critical location.
E = dynamic modulus measured in compression.
k_f1, k_f2, k_f3 = global field calibration parameters (from NCHRP 1-40D Recalibration,
k_{f1 =} 0.007566, k_f2 = –3.9492, k_f3 = –1.281).⁽⁶⁾
β_f1, β_f2, β_f3 = local or mixture field calibration factors; these factors were all set to 1.0 for the global calibration.
C = constant depending on mix properties and calculated using equations 16 and 17:

     (16)

     (17)

Where:

V_a = air voids at the time the roadway is opened to traffic (%).
V_be = effective asphalt content by volume of the mix placed on the roadway (%).
C_h = thickness correction term, and it is calculated using equation 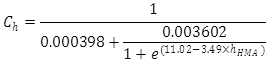18:

     (18)

The local calibration procedure is aimed at determining the calibration factors that minimize the difference between measured and predicted pavement performance. This process includes reducing bias through minimization of average prediction error and lessening error variation through reduction of the standard deviation of error. Table 1 lists the calibration factors or coefficients that need to be determined in the model calibration process for rutting and fatigue cracking in flexible pavements.

Table 1. Calibration factors in prediction models for rutting and fatigue cracking in flexible pavements.⁽³⁾

Based on the NCHRP Project 1-40B, the corresponding calibration factors in table 1 were found to be contributing to bias and standard error (STE).⁽⁴⁾ The current single-objective calibration procedure determines the calibration factors in two steps corresponding to “eliminating” bias and reducing STE, respectively.⁽³⁾ However, the multi-objective calibration approach in this research project will involve the determination of optimum values for all calibration factors to reduce bias and STE at the same time.

INPUT VARIABLES

A very important task in calibration and implementation of AASHTOWare® Pavement ME Design software is selection of accurate values for input variables. Three main categories of pavement structure, climate, and traffic variables require ample efforts to determine corresponding values for every design project. By the same token, many State agencies have sponsored research efforts to characterize local pavement materials, determine local climatic data, and classify local traffic patterns. In fact, several State agencies have developed databases or software that specify corresponding values for each input variable to be used in the implementation of AASHTOWare®.^(7,8)

The majority of the States have used LTPP data in combination with their State pavement management system (PMS) database to develop their MEPDG calibration database.^(9,10) Differences in distress identification protocols between LTPP and State PMS surveys are a source of concern regarding the combination of these data sources to be used in model calibration efforts. Some States have addressed this issue by interpreting their distress data according to the Distress Identification Manual for the Long-Term Pavement Performance Program and using the transformed data.⁽¹¹⁾

There are three levels of data precision (hierarchical input levels) for MEPDG input variables. Level 1 input values are site-specific data based on laboratory or field measurements that are the most accurate values. Level 2 values are derived based on correlations with other locally measured parameters or available historical data that were not necessarily measured at the specific site. Level 3 data are the default values that were established based on national averages, correlations, or both. Depending on the sensitivity of the predicted output to each input variable, it is important to use level 1 data when available.

Regarding asphalt material characterization in the MEPDG performance models, the most important (influential) input variable is the dynamic modulus of HMA. FHWA has developed software based on Artificial Neural Network (ANN) models to populate the LTPP database with dynamic modulus data.⁽¹²⁾ Several State departments of transportation (DOTs) have also conducted HMA material characterization studies to determine asphalt binder and mixture properties to be used as level 1 (agency-specific) input values in AASHTOWare® Pavement ME Design software.⁽¹³⁾ One of the key efforts in these studies was an evaluation of the Witczak model for calculation of dynamic modulus. Most of these studies found the Witczak model to produce reasonable predictions for dynamic modulus of HMA with conventional binders and mixtures. However, further modifications were required for binders with higher performance grades (PGs) and nonconventional mixtures, such as high recycled asphalt pavement (RAP) content, stone-matrix asphalt, cold-recycled asphalt, and warm-mix asphalt mixtures.

Most of the studies on characterization of unbound materials in flexible pavements have focused on determining resilient modulus values for typical granular aggregate base materials and local subgrade soils.⁽¹³⁾ Several studies have also developed a resilient modulus prediction model based on soil parameters. In addition, falling weight deflectometer (FWD) and other nondestructive test results have been implemented to determine the resilient modulus values. The LTPP database contains repeated load resilient modulus test results, and FWD measured deflections that could be utilized in this regard.

The LTPP database contains extensive climatic data either measured at LTPP sites or estimated from adjacent weather stations. The impact of climatic and environmental parameters on material properties of unbound pavement layers is captured using the Enhanced Integrated Climatic Model (EICM) in MEPDG. Several studies have evaluated the predictions of EICM with test data.⁽¹³⁾ Change in resilient modulus values due to seasonal variations and behavior of unsaturated soils is another topic currently under research in this area.

Traffic data inputs for the AASHTOWare® Pavement ME Design software have been calculated and are accessible for LTPP sites. LTPP data have been utilized to establish level 3 traffic inputs for the MEPDG. Several States have developed agency-specific traffic data and axle load spectra.⁽¹³⁾ Some have also developed customized software to calculate MEPDG traffic inputs from weigh-in-motion (WIM) data.

SENSITIVITY ANALYSIS OF MEPDG PERFORMANCE MODELS

Sensitivity analysis of performance prediction models is a qualitative assessment that can be implemented for multiple purposes, such as the following:

• For evaluation of the appropriate range of input variables and model parameters. The sensitive range is determined as the range within which a change in variables or parameters will result in a significant change in model output. Only the values within this sensitive range are used for model calibration and subsequent performance predictions.
  
  
• For a qualitative assessment of model function. The reasonableness of model behavior in terms of its response to increasing or decreasing input variables is evaluated against engineering principles. Model behavior can be used in the comparison of different prediction models.

This research project will include a sensitivity analysis on the final calibrated models for the second purpose. The majority of sensitivity analyses conducted on MEPDG performance models in the literature correspond to the first purpose and have been carried out before calibration. In this project, the results of the previous studies will be utilized to determine the suitable range of input variables and calibration factors. The following are two types of sensitivity analyses on MEPDG performance models in the literature:

• Sensitivity analysis of model predictions to changes in input variables.
• Sensitivity analysis of model output to variations in calibration factors.

Sensitivity to Input Variables

The most comprehensive sensitivity analysis of MEPDG performance models to changes in input variables was carried out in the NCHRP Project 01-47, and the results provide valuable information regarding range and precision of input values to be considered for calibration of each model.⁽¹⁴⁾ The adopted sensitivity metric was a Normalized Sensitivity Index (NSI), which represents percent change in predicted performance from its design limit value, normalized to a percentage change in an input variable.

This study comprised extensive one-at-a-time (OAT) sensitivity analyses in addition to comprehensive global sensitivity analysis (GSA). In contrast to the OAT analyses, the GSA varied all design inputs simultaneously across the entire problem domain. General agreements between OAT and GSA rankings of sensitivity to various input variables suggest that there were no significant interactions among design inputs. Therefore, the OAT analyses, which are computationally less demanding, could be adequate for sensitivity analysis of MEPDG performance models.

Multivariate linear regression and ANNs were utilized to fit response surface models (RSMs) to the GSA results, allowing for evaluation of sensitivities to design input variables. The ANN resulted in more accurate and robust representations of the compound relations between input design variables and output performance values. Based on frequency distributions and summary statistics generated using the ANN RSM, a “mean plus/minus two standard deviations” (m ± 2s) normalized sensitivity metric (NSI_μ±2σ) was derived, which incorporates the mean sensitivity and the variability of the sensitivity across the problem domain. This metric was used to develop the following sensitivity categories:

• Hypersensitive—NSI_μ±2σ > 5.
• Very Sensitive—1 < NSI_μ±2σ < 5.
• Sensitive—0.1 < NSI_μ±2σ < 1.
• Nonsensitive—NSI_μ±2σ < 0.1.

The hypersensitive, very sensitive, and sensitive design inputs for rutting and fatigue cracking models are listed in table 2. As indicated in this table, the performance predictions are most sensitive to the dynamic modulus (E*) of HMA layers. Poisson’s ratio and thickness of the HMA layer and the surface shortwave absorptivity are also important input variables to which these models have shown high sensitivity.

The extreme sensitivity of performance models to the lower and upper shelves of HMA dynamic modulus master curve (alpha and delta parameters) is a questionable behavior. Nevertheless, this calls for careful characterization of dynamic modulus using mix-specific laboratory measurements. In addition, accurate representation is required for thickness and Poisson’s ratio values. The most challenging insight from this sensitivity analysis is that the performance models are very sensitive to several uncertain variables, such as the surface shortwave absorptivity for HMA, thermal conductivity, and heat capacity of stabilized bases, that cannot be readily measured.

Table 2. Sensitive design inputs for rutting and fatigue cracking models.⁽¹⁴⁾ NSI_m±2s values are given in parentheses.

Sensitivity to Calibration Factors

Li et al. (2009) introduced another kind of sensitivity analysis, which is used to determine range and precision of calibration factors.⁽¹⁵⁾ This study on calibration of MEPDG flexible pavement models for Washington DOT examines sensitivity of distress output to the change in each calibration factor. This sensitivity is represented by a metric called elasticity, which was calculated as in equation 19:⁽¹⁵⁾

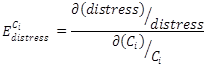     (19)

Where:

= the elasticity of calibration factor C_i for the associated distress condition.
∂ (distress) = change in distress.
distress = initial distress.

is calculated as the ratio of normalized change in predicted distress divided by the normalized change in calibration factor. A positive value means that the predicted distress increases as the calibration factor increases, and a negative value implies that the predicted distress decreases as the calibration factor increases. Based on typical pavement structure, traffic, and climatic data in the Washington DOT PMS database, table 3 indicates elasticity values for calibration factors in MEPDG rutting and fatigue cracking models.⁽¹⁵⁾

Table 3. Elasticity of MEPDG calibration factors in rutting and fatigue cracking models for Washington State DOT flexible pavements.⁽¹⁵⁾

The higher absolute values of elasticity for β_f2, β_f3, β_r2, and β_r3 indicate that model predictions are more sensitive to these calibration factors. As a result, successful calibration requires a higher degree of precision for these factors compared to the others in the optimization procedure. It should be noted that increasing the precision of calibration factors requires higher computational cost of the optimization procedure. Therefore, the selected precision for each factor should be commensurate with its corresponding elasticity.

It should also be noted that the elasticity metric needs to be identified according to the local pavement structure, climate, and traffic data. In another study on calibration of AASHTOWare® Pavement ME Design software for Iowa, Ceylan et al. used a similar sensitivity metric to calculate the change in performance prediction caused by change in calibration factors.⁽¹⁶⁾

STATE CALIBRATIONS OF MEPDG PERFORMANCE MODELS

Global calibration and validation of MEPDG performance models were completed using a subset of LTPP data based on national averages.⁽²⁾ Ever since, numerous State DOTs have been in the process of calibrating these models to their own regional materials–traffic–climate conditions. Two important studies of NCHRP 9-30 and NCHRP 1-40B have provided guidelines in this regard.^(17,4) The NCHRP Synthesis 457 provides a comprehensive report on the pavement design practices and MEPDG implementation status in various States across the country.⁽¹⁰⁾ This report also includes agency implementation challenges and details case examples of the MEPDG implementation process in three States.

NCHRP 1-40B provides the following 11-step procedure for verification, calibration, and validation of the MEPDG models for local conditions, which has been adopted by AASHTO:⁽³⁾

1. Select hierarchical input level.
2. Develop experimental plan and sampling template.
3. Estimate sample size.
4. Select roadway segments.
5. Evaluate project and distress data.
6. Conduct field testing and forensic investigation.
7. Assess local bias.
8. Eliminate local bias.
9. Assess STE of the estimate.
10. Reduce STE of the estimate.
11. Interpret the results.

Statistical significance testing is recommended at various steps to determine if the models need further calibration. At the seventh step, the significance of the bias (the average difference between predicted and measured performance) is tested. If there is a significant bias in prediction of pavement performance measures, the first round of calibration is conducted at the eighth step to eliminate bias. For example, during this step for the rutting models, the SSE is minimized by adjusting the β_r1, β_GB, and β_SG calibration factors.

At the ninth step, the STE (standard deviation of error among the calibration dataset) is evaluated by comparing it to the STE from the national global calibration. If there is a significant STE, the second round of calibration at the 10th step tries to reduce the STE by adjusting the β_r2 and β_r3 calibration factors. A final validation step checks for the reasonableness of performance predictions. The flowcharts depicted in figure 1 and figure 2 demonstrate this calibration process.⁽³⁾

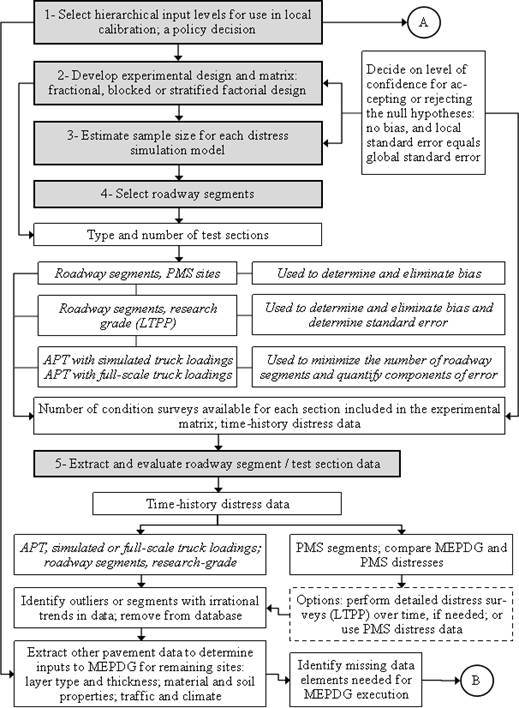
Reprinted from Guide for the Local Calibration of the Mechanistic–Empirical Pavement Design Guide, 2010, by the American Association of State Highway and Transportation Officials, Washington, DC. Used by permission.

Figure 1. Flowchart. The AASHTO recommended procedure for local calibration of MEPDG performance models, steps 1 through 5.⁽³⁾

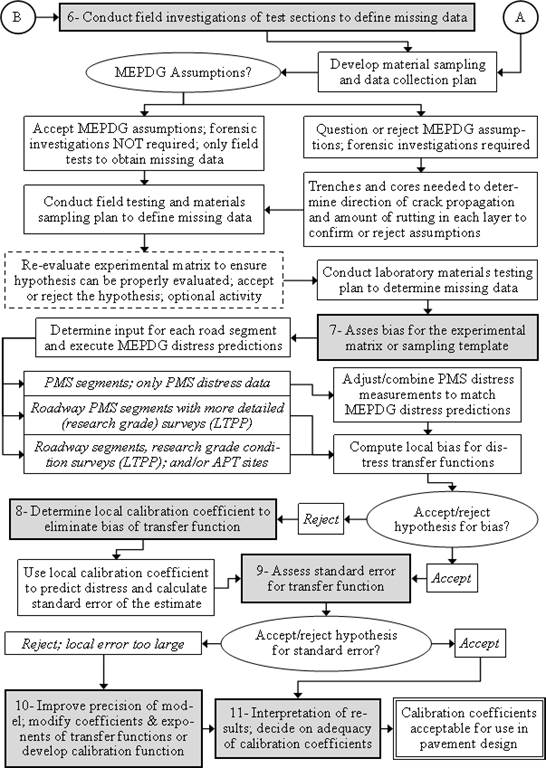
Reprinted from Guide for the Local Calibration of the Mechanistic–Empirical Pavement Design Guide, 2010, by the American Association of State Highway and Transportation Officials, Washington, DC. Used by permission.

Figure 2. Flowchart. The AASHTO recommended procedure for local calibration of MEPDG performance models, steps 6 through 11.⁽³⁾

The most recent literature review on calibration of MEPDG in different States was conducted as part of a study for Georgia DOT.⁽¹³⁾ Results of this literature review and other similar studies have been compiled to provide a summary of the State calibration efforts in table 4 and a list of reported calibration factors for flexible pavement fatigue cracking and rutting models in table 5.

Most of the past calibration studies suggest that the MEPDG rutting prediction models overpredict rutting in unbound pavement layers. However, the rutting predicted in asphalt concrete (AC) layers seems to be easily calibrated. The fatigue (alligator) cracking model seems to underpredict actual pavement distress and has high variation in the predicted values. There seems to be little to no problem in calibration of transverse cracking and smoothness prediction models. There seems to be no specific trend for the flexible pavement longitudinal cracking model, and none of the studies reported a successful calibration of it. The MEPDG longitudinal cracking model is not considered in the scope of this study because several past studies have expressed concern on the lack of fit of this model.⁽¹⁸⁾ Difficulty in differentiating longitudinal cracks in the wheelpath from alligator cracking patterns might have contributed to errors in measured longitudinal cracking values.

Differences among various distress identification protocols (e.g., LTPP versus State PMS) and the subjective nature of identifying distress type and severity have been noted as sources of measurement error that cause significant challenges in calibration of mechanistic models to field-measured performance data.^(19,20)

Table 4. Major State efforts for calibration of MEPDG performance models.

Table 5. Local calibration factors for MEPDG fatigue cracking and rutting prediction models.

Table 5 shows significant variance among the States in terms of the β_f1, β_f2, β_f3, β_r1, β_GB, and β_SG calibration factors as indicated by their corresponding high coefficients of variation. Therefore, it is important that the optimum coefficients be determined for these calibration factors to ensure compliance to local pavement performance. In addition, C₁ and C₂ also show some variation among different calibration efforts. The number of calibration factors determined to be equal to 1 (1.0), which are the global calibration values, are more for the fatigue cracking model compared to the permanent deformation model. This could be interpreted as a superior global model having been developed for fatigue cracking compared to rutting.

OTHER MEPDG CALIBRATION EFFORTS

The measurement error in the performance data records is known to be greatly undermining precision of calibrated MEPDG models.⁽¹⁸⁾ Therefore, Hall et al. suggested a new output format for the performance models to predict ranges of distress instead of an exact value.⁽²⁷⁾

To account for the effect of maintenance or rehabilitation activities, Li et al. suggested developing piecewise performance models for Washington State.⁽³⁰⁾ Pavement serviceable life was divided into three time periods of early age, rehabilitation, and overdistressed situations. They used regression to develop models for each time period.

In addition to the national research studies conducted to determine the global calibration factors for permanent deformation model, some States have conducted their own laboratory tests in this regard.⁽³¹⁾ For example, Jadoun and Kim used results of the triaxial repeated load permanent deformation test to determine the global k factors for 12 different HMA mixtures.⁽³²⁾

The majority of these studies used exhaustive search methods such as the generalized reduced gradient (GRG) method to minimize SSE between measured and predicted performance. These methods are local optimization techniques that are dependent on seed values and typically get stuck at a local minimum of error. Jadoun and Kim compared a genetic algorithm (GA) to the GRG method for calibration of rutting and fatigue cracking models for North Carolina.⁽³²⁾ They demonstrated that the GA method provides a more global minimum of SSE compared to the GRG method in predicting rutting. However, this superior optimization does not result in a reasonable match between predicted and measured fatigue cracking.

It should be noted that the applied GA code is highly sensitive to the control parameters used to manipulate the evolutionary process of optimization. Therefore, there might be variants of this GA code that perform better, and the best set of control parameters needs to be determined for each optimization problem. Several evolution strategies (ESs) have been developed in the evolutionary computation literature that evolve and adapt control parameters along with optimization solutions and with respect to the objective function space. Application of these ESs would result in a more robust optimization.

MULTI-OBJECTIVE CALIBRATION STUDIES

All of the MEPDG calibration studies focus on minimization of a single-objective function (SSE) for all distress severity levels and all pavement ages in the considered network. Incorporating multiple sources of information might reveal unknown aspects of this calibration problem and result in more reasonable calibration coefficients. Multi-objective evolutionary algorithms (MOEAs) are derivative-free, global optimization heuristics that provide a set of tradeoff solutions independent of seed values.⁽³³⁾

MOEAs have been used in pavement management studies to optimize the allocation of resources to various treatment alternatives considering multiple criteria.^(34–36) They have also been vastly implemented in water resources research to design long-term groundwater monitoring schemes and to calibrate hydrologic models.^(37,38) The multi-criteria framework provided by this kind of calibration has enabled recognition and handling of errors and uncertainties and detection of prominent behavioral solutions with acceptable tradeoffs in hydrologic modeling efforts within the past decade.⁽³⁹⁾

INSIGHTS AND OBSERVATIONS FROM THE LITERATURE REVIEW

The following are the key observations drawn from this literature review:

• Different data sources are being incorporated in the MEPDG calibration process, but attention should be paid to the differences in performance measurement protocols.
  
  
• The sensitivity of performance models to the HMA dynamic modulus, thickness, and Poisson’s ratio calls for careful characterization of these values. MEPDG performance models are very sensitive to several uncertain variables, such as the surface shortwave absorptivity for HMA, thermal conductivity, and heat capacity of stabilized bases, that cannot be readily measured.
  
  
• Model predictions are more sensitive to some local calibration factors compared to others. Therefore, the selected precision for each factor should be commensurate with its corresponding elasticity.
  
  
• MEPDG rutting and fatigue cracking models have been reported to overpredict and underpredict actual pavement distresses, respectively. The local values calculated for the calibration factors, β_f1, β_f2, and β_f3 for fatigue cracking model and β_r1, β_GB, and β_SG for rutting model, seem to be significantly different among various reviewed calibration efforts.
  
  
• Differences among various distress identification protocols (e.g., LTPP versus State PMS) and the subjective nature of identifying distress type and severity have been noted as sources of measurement error that cause significant challenges in calibration of mechanistic models to field-measured performance data.
  
  
• Due to the challenge posed by distress measurement errors, some researchers have proposed conducting model calibration using ranges of distress instead of exact values. Furthermore, to account for different pavement behavior during its various life stages, it has been suggested that model calibration be carried out separately across different periods of pavement service life.
  
  
• Global heuristic optimization methods, such as evolutionary algorithms (EAs), could possibly identify a more optimum set of calibration coefficients compared to the local exhaustive search methods.
  
  
• The multi-criteria calibration framework provided by MOEAs has enabled recognition and handling of errors and uncertainties and detection of prominent behavioral solutions with acceptable tradeoffs in hydrologic modeling efforts.

IMPACT ON RESEARCH APPROACH

Based on the findings of this literature review, the following considerations corresponding to the above observations were recommended for the research approach:

• This study should be performed using LTPP data for flexible pavements within a specific region comprising one or more States with similar climatic and subgrade conditions. In addition to LTPP data for the selected region, utilization of another source of data, such as State PMS or APT data, should be considered.
  
  
• Careful characterization of the HMA dynamic modulus, thickness, and Poisson’s ratio is necessary for the success of this project. In this regard, the results of ANNs for Asphalt Concrete Dynamic Modulus Prediction (ANNACAP) software for LTPP test sections should be implemented. This software could be used for non-LTPP data sources when applicable.
  
  
• The selected precision for each factor in the optimization procedure should be commensurate with the corresponding sensitivity of the performance model to that calibration factor. This is an important consideration because the precision of these unknown variables directly relates to the computational cost of the optimization problem.
  
  
• This research project will focus on local calibration of prediction models for rutting on new and overlaid flexible pavements.
  
  
• The multi-objective calibration approach could incorporate the different data characteristics (performance measurement protocols) of different data sources in an objective manner.
  
  
• Using a multi-objective calibration approach and by simultaneously minimizing the error in predicting pavement performance from disparate data sources, the calibration coefficients that provide a tradeoff among pavement behavior during different experiments will be determined.
  
  
• In this study, MOEAs will be implemented. These global optimization heuristics have good global search ability, are less dependent on seed values (techniques such as restarting have been shown to significantly decrease dependence on seed values), and do not require the mathematical formula (to find the derivative) of the objective functions.⁽³⁷⁾
  
  
• Using MOEA, multiple sources of information can be incorporated in an objective manner, resulting in a final set of tradeoff solutions. This way, none of the possible sets of calibration factors will be eliminated prematurely, and all of the nondominated solutions will be included in the final tradeoff front. Exploring the final front might reveal unknown aspects of this calibration problem and result in more reasonable calibration coefficients that could not be identified using single-objective approaches.

Several scenarios can be devised for multi-objective formulation of calibration, all of which could overcome cognitive challenges and add to the knowledge of this problem. More than one set of multiple objectives will be considered to explore new aspects of the calibration problem. The idea is to optimize multiple objectives simultaneously. The following are the proposed sets of objectives up to this stage of the study:

• Statistical outcomes (increasing accuracy and precision simultaneously).
  1. Minimize average error (bias).
  2. Minimize error standard deviation.
• Data sources (an objective approach to incorporate different sources of data).
  1. Minimize error on LTPP data.
  2. Minimize error on APT data.

In the primary multi-objective scenario, mean and standard deviation of prediction error are simultaneously minimized to reduce the bias and STE at the same time. In this manner, the information from a single calibration run is fully implemented, and an additional round of computationally intensive calibration is avoided.

In the second multi-objective scenario for calibration of MEPDG performance models, the error in predicting the performance of pavements within different performance data sources will be used as separate objective functions to be minimized simultaneously. In addition to LTPP test sections, data from State PMS or APT facilities in the same region can be considered for this scenario. This scenario comprises an objective approach to incorporate different sources of data. Finally, a combination of two or more of the above scenarios could also be considered for the multi-objective calibration approach.

^[1] For consistency with how measurements are recorded in the LTPP database, all layer thickness measurements are presented in inches in this report. These measurements can be converted to centimeters: 1 inch = 2.54 cm.