U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-104 Date: June 2018 |
Publication Number: FHWA-HRT-17-104 Date: June 2018 |
In the proposed approach for the execution of this research project, task 4 was anticipated for all the programming activities that were needed to implement a multi-objective calibration of the MEPDG performance models. An overview of the general programming activities is described in the following sections of this report. First, the approach to implement the AASHTO recommended calibration (single-objective) is presented. Second, the multi-objective evolutionary optimization framework is outlined. Third, the methodology for calculation of the predicted performance using MEPDG is explained. And finally, the multiple considered objective functions and their corresponding calculations are clarified.
The plan for task 3 of this research project was to use the available AASHTOWare® Pavement ME Design software to conduct a conventional single-objective calibration according to the AASHTO guidelines, the results of which would serve as a comparison baseline. In this manner, this study will compare the multi-objective approach against a single-objective approach currently being used by the State agencies.
NCHRP 1-40B provides an 11-step procedure for verification, calibration, and validation of the MEPDG models for local conditions, which has been adopted by AASHTO.(4,3) At the seventh step, the significance of the bias (the average difference between predicted and measured performance) is tested. If there is a significant bias in prediction of pavement performance measures, the first round of calibration is conducted at the eighth step to eliminate bias. During this step, the SSE is minimized by adjusting the βr1, βGB, and βSG calibration factors.
At the ninth step, the STE (standard deviation of error among the calibration dataset) is evaluated by comparing it to the STE from the national global calibration. If there is a significant STE, the second round of calibration at the 10th step tries to reduce the STE by adjusting the βr2 and βr3 calibration factors. A final validation step checks for the reasonableness of performance predictions.
The AASHTO guidelines provide regression equations for calculating the STE for each sublayer (AC, granular layers, and fine-grained layers). These equations were initially developed, not based on trenching data, but based on a “systematic approach” of assigning a fraction of the total measured rutting to each layer. During the NCHRP Project 09-30A, some trenching experiments were conducted.(31) However, the STE equations for each layer have not actually been updated accordingly. Only the STE regression equation for the total pavement rutting was updated following that study. In the absence of trenching data, only the STE in calculating the total pavement rutting is compared to the STE from the global calibration, which was about 0.1 inch.
Global heuristic optimization methods such as EAs could possibly identify a more optimum set of calibration coefficients compared to the local exhaustive search methods. That is why in this project an EA is used for each step of the required single-objective optimization to calibrate the rutting models for new and overlaid pavements.
The single-objective calibration process is used in calibrating rutting models for new AC pavements using LTPP SPS-1 Florida site data and overlaid AC pavements using LTPP SPS-5 Florida site data.
In this research project, MOEAs have been implemented to optimize the multiple objective functions involved. Using a multi-objective optimization approach allows escaping preconception, avoiding excessive concentration on only one aspect of the problem, and combining multiple sources of information in an objective manner.
MOEA Framework (moeaframework.org) is a free and open-source Java framework for multi-objective optimization using a variety of EAs, including GAs and ESs. In this object-oriented framework, an instance of the “abstract problem” class needs to be created, in which the calculation process for the multiple objective functions is implemented. Then an instance of the “problem execution” class is created, where the abstract multi-objective optimization problem is solved using a selected “algorithm.”
At the first round of programming for this project, a Java code was developed to integrate the performance model engine of the AASHTOWare® Pavement ME Design software and the multi-objective EA into a calibration software as indicated in figure 15. After creating all the input data files for all the calibration test sections, the ME Design software was executed once to generate the materials properties, climate, traffic, and pavement response files. The framework runs the Asphalt Pavement Analysis and Design System (APADS) software using these files and the updated calibration factors at each iteration to calculate the MEPDG rutting values.(1) A comparison of these calculated values to LTPP measured values is used to evaluate the multiple objective functions (error functions) for each of the calibration factor sets. The MOEA then updates the solution population members (calibration factor sets) according to the results of objective function evaluations.

Source: FHWA.
Figure 15. Flowchart. Multi-objective calibration framework.
If improving final optimization solutions in terms of one objective degrades them in terms of other objectives, there is a conflict between the objectives; a clear example is the cost–performance tradeoff. When there is no conflict between multiple objectives, they can be combined using an engineered weighing scheme, and the problem would change into a single-objective optimization. The general goal of any multi-objective optimization is to identify the Pareto-optimal tradeoffs between multiple objectives. It is called a Pareto-optimal tradeoff because the best compromise among the multiple conflicting objectives is sought, and it was defined by Vilfredo Pareto (1896).(55) A Pareto-optimal solution has at least one better objective value compared to any other feasible solution in the decision space, while performing as well or worse in all remaining objectives. A solution X1 is called dominated if and only if another feasible solution X2 performs better than X1 in terms of at least one objective and as well as X1 in terms of others. A set of Pareto-optimal solutions is called the nondominated or Pareto-optimal front.
EAs have good global search ability, are less dependent on seed values, and do not require the mathematical formula to take the derivative of the objective functions.(56) In addition, EAs seem more suitable for multi-objective optimization because they are population based (they find several members of the Pareto-optimal front in a single run of the algorithm instead of having to perform a series of separate runs) and are less sensitive to the shape and discontinuities in the Pareto-optimal front.(33) A multi-objective GA called epsilon-dominance nondominated sorted GA (NSGA)II (ε-NSGAII) is implemented for multi-objective calibration.(57) ε-NSGAII has performed better in terms of effectiveness, efficiency, and reliability compared to other evolutionary multi-objective algorithms on complicated water resources applications.(57,58) It is also demonstrated to be easier to implement than traditional multi-objective EAs due to its simplified parameterization, adaptive population sizing, and automatic termination.(57)
The ε-NSGAII was designed based on an earlier successful second-generation multi-objective GA, the NSGAII, while the first-generation algorithm was called NSGA.(59,60) NSGA implemented the nondomination sorting approach recommended by Goldberg.(61) Fitness is assigned based on the level of domination (number of solutions that dominate the solution being evaluated) and similarity of solutions (i.e., fitness sharing). NSGA’s front-based fitness assignment ensures that the solutions are found along the full extent of the Pareto front. NSGAII improved upon NSGA by implementing a more efficient nondomination sorting scheme, eliminating the need to specify the sharing parameter, and adding elitism and crowded tournament selection.(59) Following real-parameter simulated binary crossover (mating) and polynomial mutation, the N best individuals are selected from the combination pool of parent and child populations, preserving the elite population members. The two-step crowded tournament selection favors the individuals with lower rank (dominated by fewer other solutions), and if two solutions share the same rank, the solution with larger crowding distance is preferred (crowding distance is the largest cuboid surrounding the solution, in which no other solutions are present). NSGAII’s extensive problem-specific parameter calibration was minimized in ε-NSGAII using epsilon-dominance archiving, adaptive population sizing, and automatic termination.(57)
Taking advantage of the epsilon-dominance concept, the user can specify the precision to quantify each objective. In the first step, the search space of the problem is divided into grid blocks, each block having a width of epsilon based on the specified precision. According to the developers of the algorithm, “Larger ε values result in a coarser grid (and ultimately fewer solutions) while smaller values produce a finer grid.”(57) Epsilon can be viewed as publishable precision or error tolerance determined to avoid wasting computational resources on unjustifiably precise results.(62) If there are multiple solutions in a grid block, only the solution closest to the lower left-hand corner of the block is saved (assuming minimization of all objectives). Step 2 comprises nondomination sorting based on the grid blocks. In this step, each grid block is used as a reference, and any other solution grids to the top and right side of the reference grid will be eliminated.(57) Step 3 is called “thinning of solutions,” where dominated solutions are eliminated. As a result, a more even search of the objective space is encouraged.
The ε-NSGAII starts with exploiting small populations to “precondition” search, and then it automatically adapts population size according to problem difficulty and explores further areas of the solution space.(57) This is carried out through a series of “connected runs.” An offline archive is used to store epsilon-nondominated solutions found after each generation, which are subsequently used to direct the search in the next run. While the search is directed using previously evolved solutions (25 percent elitism among runs), adding new random solutions (75 percent) encourages the exploration of additional regions of the search space.(57) If the number and quality of nondominated solutions does not increase above a minimum threshold (delta parameter) between two successive runs, the algorithm is automatically terminated across all populations. The initial use of smaller population sizes, the elimination of random seed analysis, and the elimination of trial-and-error application runs to determine search parameters are all contributing to lower computational cost.
The probability of mating and mutation are assumed to be 1 and 1/n, respectively, with n being the number of unknown parameters to calculate (number of calibration factors in this case). The initial population size is assumed 10, and the maximum number of generations per run is 250. The search is terminated after 10,000 function evaluations unless terminated due to the delta parameter of 10 percent beforehand.(58)
After executing the preliminary runs of the developed program, it was found that each evaluation using the APADS software takes about 4 min to complete. This is because APADS conducts both the pavement analysis to calculate responses and then the calculation of pavement performance. However, pavement responses do not change by changing the calibration factors in consecutive iterations, and there is no need to conduct pavement analysis at every iteration. There was no option to calculate only the pavement performance using the responses. While the APADS software was launched simultaneously for all the LTPP test sections used in the calibration database, each optimization iteration was taking about 30 min to evaluate all the solution population members (calibration factor sets) on all the calibration data (using a computer with Intel Core i7-4600 2.1 GHz and 8 GB of RAM). Since the complete calibration could take hundreds of iterations, it was not feasible to continue using the APADS software in this framework. Therefore, it was decided to simulate the Pavement ME software to replace the APADS routine in this framework.
As explained above, due to the long computational time of the APADS analysis software, it was decided to use the MEPDG equations to calculate pavement performance based on the generated materials properties, climate, traffic, and pavement response data files. The calculation of total pavement deformation using these equations was embedded in the code for objective function evaluation, which involves calculation of the difference between measured and calculated rutting. The following sections explain how these calculations were conducted to simulate the performance predictions in the Pavement ME software.
The total rutting is the summation of each layer permanent deformation. Pavement ME software calculates the monthly incremental pavement total deformation for the design life. The expression to calculate total pavement deformation when the pavement structure is composed of HMA layer(s) and granular base (GB) layer(s), on top of a fine-grained subgrade, is in equation 34:
![]() (34)
(34)
Where:
RD = total pavement permanent deformation.
RDHMA= HMA layer permanent deformation.
RDGB= GB permanent deformation.
RDSG= fine-grained subgrade permanent deformation.
hHMA= thickness of the HMA (inches).
εp(HMA)= permanent strain of the HMA layer.
δa(GB)(N) = permanent or plastic deformation for granular material.
δa(SG)(N) = permanent or plastic deformation for fine-grained materials.
The initial round of rutting calculation with global calibration factors (local factors set to 1.0) was done using the Pavement ME software. Subsequent rutting calculation within the optimization framework was done using a simulated approach based on the MEPDG equations to save computational time. This process can be done efficiently, since pavement temperature, number of axle load repetitions, and elastic strain do not need to be recalculated for each new set of local calibration factors. The AASHTOWare® output files that provide the data for the global rutting calculation are described in table 25.
Table 25. AASHTOWare® Pavement ME Design software data files.
| Data Item | Software File | Data Field/Value |
|---|---|---|
| Layer thickness | input.tmp | Material thickness |
| Water content | input.tmp | Initial water content |
| Local and global calibration factors | calibrationfactor.dat | HMA rutting (columns 4, 5, 6), subgrade rutting (columns 1, 3) |
| Cumulative traffic per month | TruckGrowth.csv | Column 2 |
| Noncumulative number of trucks in each class per month | TruckGrowthByClass.csv | For each class |
| Hourly temperature | thermal.tmp | Column# = Round(0.3681hac + 2.2857, 0) |
| Vertical strain in each subseason under each axle type and at different horizontal locations under the load | _VertStrain.txt | Strain |
| Rutting per layer | rut.tmp | AC1, GB2, SG3, Total |
Most of the data files generated by the Pavement ME software include data at a monthly frequency, except for the thermal.tmp file, which includes hourly pavement layer temperature values. It appears that the APADS software is calculating rutting values on a submonthly basis. Each “subseason” is one-fifth of the month, which includes one-fifth of the total monthly traffic and an average temperature for a 20-percent percentile of a normal distribution generated based on hourly temperature data in that month. A normal distribution histogram is generated based on hourly temperature data in each month, and the area under the histogram is divided into five identical slices. Each slice indicates one subseason, and the centroid of each slice is used as the average temperature for that subseason. The software then cumulates the calculated rut depth values for the five subseasons in the month to calculate the monthly rutting. The _VertStrain file includes vertical strain in each subseason, under each axle type, and at different horizontal locations under the load. However, it is not clear which depth (layer) of the pavement structure these strain values are calculated for. Since the available data files do not contain adequate details on the intermediate pavement response data, it was decided to simulate the software output instead of using the documented process in the AASHTO Manual of Practice.(51)
Note: The simulation process explained here onward is not the same procedure that the AASHTOWare® Pavement ME Design software is using to calculate rut depth (according to the AASHTO Manual of Practice). The following sections explain the simulation methodology for calculating rutting in asphalt bound and unbound pavement layers.
For better accuracy in simulating the ME software calculations, the permanent deformation in the AC layers was assumed to be calculated on an hourly basis instead of a subseason basis. The general shape of the rutting prediction model was used to conduct this simulation, assuming rutting and traffic to be cumulative values (note that in the original MEPDG equation, this is only true if the temperature was constant in this period, as it is in laboratory tests). The hourly temperature in each pavement layer is available in the thermal.tmp file. The available cumulative monthly traffic and calculated global rutting prediction were transformed linearly to cumulative hourly values (which is again an assumption used for this simulation and not necessarily true). After this transformation, the hourly strain is backcalculated with equation 35 for the global model with local calibration factors equal to 1. This is because the available monthly maximum vertical strain data (_VertStrain.txt) for each axle type (single, tandem, tridem, quad) could not be attributed to a specific pavement layer and were not readily transformed to hourly values. As noted previously, an hourly period is used to achieve better accuracy in simulating the software results.
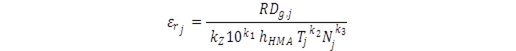 (35)
(35)
Where:
εrj = backcalculated resilient or elastic strain for hour j.
RDg,j = HMA permanent deformation calculated using MEPDG software for global calibration factors (g stands for global); the total amount of rutting accumulated up to hour j in each month i is calculated (assuming linear increase in rutting within each month) using equation 36:
![]() (36)
(36)
Where:
i = month.
j = hour.
di = total number of days in the month i.
Hj = number of hours from the beginning of each month up to hour j.
For D in equation 2, Dm is used, which is the depth below the surface for each HMA layer m calculated using equation 37:
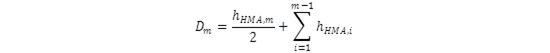 (37)
(37)
Where:
m = HMA layer number from top to bottom.
k1, k2, k3= global field calibration parameters.(6) k1 = –3.35412, k2 = 1.5606, k3 = 0.4791.
hHMA = thickness of the HMA sublayer/layer (inches).
Tj = layer temperature for hour j from thermal.tmp file.
Nj = number of axle load repetitions up to hour j (assuming linear increase in traffic within each month) calculated using equation 38:
![]() (38)
(38)
The subsequent monthly rutting calculations for each month i and any different set of calibration factors can be done using the above backcalculated hourly strain values in equation 39:
![]() (39)
(39)
Where:
RDHMA,i = total HMA permanent deformation accumulated up to month i.
βr1, βr2, βr3 = local or mixture field calibration factors.
This approach was tested through a comparison of the Pavement ME software results with various pavement structures and different local calibration factors. Examples for the comparison of this simulated calculation to the ME software can be found in appendix C. It should be noted that the same approach was used for ATB layers. Figure 16 shows an example comparison of the simulated total pavement rutting to the Pavement ME software output. As evident in this figure and similar figures in appendix C, the simulated calculation and the software output follow a similar trend. While there are some intermediate decrements in rutting values simulated within each month, the total accumulated rutting at the end of each month is very close to the software output. The reason for the intermediate decrements (which do not comply with the theory of rutting accumulation) is the assumptions made for the simulation, which may not be inherently correct. One of those assumptions is that traffic and rutting values are increasing linearly within each month, which might not be true. As explained before, the actual subseason pavement response data for each layer are not provided by the AASHTOWare® software, and therefore, an exact calculation (according to the MEPDG equations) could not be conducted for this project.
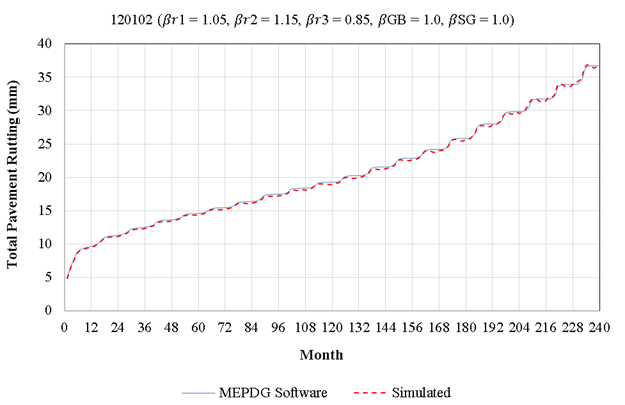
Source: FHWA.
Figure 16. Chart. Example comparison of the simulated calculation to Pavement ME software output (on SPS-1 test section 120102).
A similar approach was applied for the coarse- and fine-grained unbound layers. The relationship between the calculated elastic strain and the laboratory resilient strain is backcalculated for the global model using equation 40:
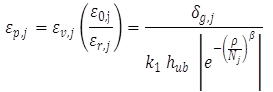 (40)
(40)
Where:
εp= permanent vertical strain.
εv = vertical resilient or elastic strain in the layer calculated by the structural response model.
δg,j= permanent or plastic deformation for granular and fine-grained materials calculated by the Pavement ME software for the global calibration factors; the total amount of rutting accumulated up to hour j in each month i is calculated using equation 41:
![]() (41)
(41)
Where:
k1 = global calibration coefficient.
k1 = 2.03 for granular materials.
k1 = 1.35 for fine-grained materials.
hub= thickness of the unbound layer/sublayer (inches).
Nj= number of axle load repetitions up to hour j.
Knowing the initial relationship among permanent and resilient strains and then rutting in each unbounded layer with any set of local calibration factors is calculated using equation 42:
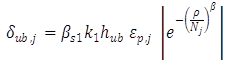 (42)
(42)
Where:
δub,,j= permanent or plastic deformation for granular and fine-grained materials accumulated up to hour j.
βs1 = local calibration factor.
In this section, the concept and equations for calculation of each objective function have been outlined. These objective functions quantify the multiple sources of information that could be combined to enhance model calibration. These multiple objective functions will be optimized simultaneously to determine the calibration coefficients that provide a tradeoff among the various objectives.
Several scenarios can be devised for multi-objective formulation of calibration, all of which could overcome cognitive challenges and add to our knowledge of this problem. More than one set of multiple objectives will be considered to explore new aspects of the calibration problem. The following are the identified approaches and the multiple objective functions that need to be simultaneously minimized for each scenario:
In the first alternative scenario, mean and standard deviation of prediction error are simultaneously minimized to reduce the bias and STE (increase model accuracy and precision) at the same time. In this manner, the information from a single calibration run is fully implemented, and an additional round of computationally intensive calibration is avoided. This two-objective optimization will be separately executed in calibrating rutting models for new AC pavements using LTPP SPS-1 Florida site data and overlaid AC pavements using LTPP SPS-5 Florida site data.
In the second scenario, the SSE and STE in predicting permanent deformation of pavements within different performance data sources will be used as separate objective functions to be minimized simultaneously. This four-objective optimization will be used in calibrating rutting models for new AC pavements using the LTPP SPS-1 Florida site data and the FDOT APT data at the same time. This scenario will comprise an objective approach to incorporate different sources of data. This scenario was not applied to overlaid pavements because the available APT data were only for new pavement structures.
As explained before, when there is no conflict between multiple objectives, they can be combined using an engineered weighing scheme, and the problem would change into a single-objective optimization. However, in the case of the selected objective functions in this study, the existence of a conflict cannot be proven theoretically. In the case of the second scenario, the sources of data for multiple objective functions are different, and the errors on LTPP and APT data may or may not be in conflict. In the case of the first scenario, equations 43 and 44 are the expanded expressions for calculating SSE and STE, which are to be minimized.
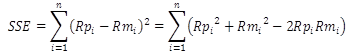 (43)
(43)
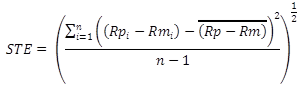 (44)
(44)
Where:
n = the number of rutting data records.
Rpi= the predicted (for a specific pavement structure at a specific time) rutting record i.
Rmi = the corresponding measured rutting record i.
Equation 45 is an expanded expression for STE from equation 44.
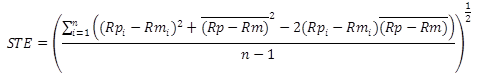 (45)
(45)
For different sets of calibration factors, the SSE and STE (from equations 43 and 45) could be increased or decreased either in the same or the opposite direction of each other. A set of calibration factors that results in the minimum SSE does not necessarily guarantee a minimum STE. This means that a calibrated model that exhibits higher accuracy (lower SSE) might not necessarily have higher precision (lower STE) as well. As it cannot be proven whether the selected objective functions are in conflict, they cannot be combined with the goal of simplifying the problem into a single-objective optimization. Therefore, a multi-objective optimization approach was used.