U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-064 Date: August 2014 |
Publication Number: FHWA-HRT-14-064 Date: August 2014 |
This application guide describes a simplified procedure for assessing fish passage at low flows, recognizing velocity variations in the flow field. The procedure employs existing tools, such as HY-8, for making many of the computations needed for the procedure, including computation of composite roughness, flow depth, and average velocity. FHWA anticipates further modifications to HY-8 that will completely automate the calculations needed for this procedure.
FHWA and others have provided comprehensive guidance for the use of stream simulation to design for fish passage, but as described previously, stream simulation may not be appropriate for all situations. This procedure employs the fish passage path width concept with the simplified design charts developed in this research report.
The first part of this guide describes the basic steps of the process, referring the reader to other standard references for computational details. The second part includes example computations for three embedded culvert design situations. The first two include circular culverts, and the third considers a box culvert.
The simplified design procedure for assessing fish passage in a culvert is composed of five steps. Most of the steps rely on well-established methodologies described in other references. The design charts provided in this report are used in step 5.
A culvert may be initially sized or assessed using a peak discharge developed using traditional methods. The design flows of interest for fish passage are those that are relevant to the periods when fish require passage through the culvert. As described in detail in HEC 26, this range is bounded by the low passage flow, QL, and the high passage flow, QH.(1) HEC 26 provides guidance on how those flows are determined, with the first priority being site-specific guidance provided by the appropriate Federal, State, or local regulatory authority.
HEC 26 goes on to explain that in the absence of site-specific guidelines, the QH should be defined as either the 10-percent exceedance quantile on the annual flow duration curve or 25 percent of the Q2, in that order of preference. Similarly, in the absence of site-specific guidance, QL should be defined as either the 90-percent exceedance quantile on the annual flow duration curve or the 7-day, 2-year low flow (7Q2), whichever is smaller. Regardless of the source of the estimate, QL should not be lower than 1 ft3/s. More detailed information is provided in HEC 26.
Step 2. Estimate Flow Depth and Composite Roughness
For an embedded culvert, the wetted perimeter of the flow includes two different materials, culvert and stream bed, and therefore two different roughness values. The values for the culvert material can be taken from standard hydraulic references, such as HDS 5, and the values for stream bed materials are available in a variety of references.(18)
HEC 26 provides a summary of several methods appropriate for estimating Manning's n value for bed materials. The method presented in the main report is the Blodgett equation, which performs well for the range of conditions encountered for fish passage design.(1) The Blodgett equation is shown in figure 108.
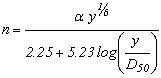
Figure 108. Equation. Blodgett's equation for bed roughness
Where:
n = Manning's roughness, dimensionless.
y = Flow depth, ft.
D50 = Median grain size, ft.
α = 0.262 in customary units and 0.319 in metric units.
Once the Manning's roughness values for the culvert wall and bed material are determined, a composite roughness value is needed. The equation recommended in this study is provided in figure 109.
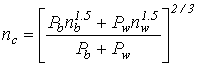
Figure 109. Equation. Composite roughness
Where:
nc = Composited n-value for the culvert.
Pb = Wetted perimeter of the bed material in the culvert.
nb= n-value of the bed material in the culvert.
Pw= Wetted perimeter of the culvert walls above the bed material.
nw= n-value of the culvert material.
This equation is also used in HDS 5 and recommended in the research work of Tullis.(29) It is also used in HY-8 so that a designer using this tool will only need to enter the individual roughness values, and HY-8 performs the compositing computation.
Step 3. Compute Water Surface Top Width and Average Velocity
The flow profile in the culvert is needed to determine the average velocities throughout the culvert length. The most conservative location to assess from a fish passage perspective is the location in the culvert with the lowest depth because this will be the location with the highest velocity. A computer program such as HY-8 or HEC-RAS may be used for this purpose.
The water surface top width is also required. For a circular conduit, the water surface top width, T, is a function of the culvert diameter, D, the depth of embedment, de, and the maximum flow depth, ymax, as shown in figure 110. It is calculated using the equation in figure 111.
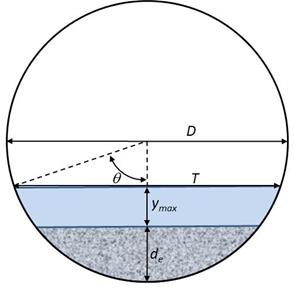
Figure 110. Illustration. Definition sketch for geometric parameters
![]()
Figure 111. Equation. Water surface top width
Where:
T = Top width of the water surface, ft.
D = Culvert diameter, ft.
θ = Angle between a line to the water surface at the edge of the pipe from the center of the pipe to the vertical.
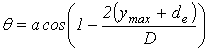
Figure 112. Equation. Angle to water surface
Where:
ymax = Maximum flow depth, ft.
de = Embedment depth, ft.
Step 4. Find Appropriate Fish Swimming Characteristics
Use of this simplified design procedure requires identification of the required depth and velocity limits for passage for target fish species. The species of interest will likely be specified by the appropriate regulator or by a design team member with expertise in fish biology. In many cases, written guidance may be found in State or local design manuals. HEC 26 provides a national overview of fish biology and swimming capabilities.
The parameters required for design are maximum allowable fish passage velocity, Vf, and minimum depth required for fish passage, yf, in the culvert for the range of conditions between the low and high passage flows. In some cases, the length of the culvert may also be relevant because fish can only swim against higher velocities for a limited duration before tiring. If the culvert is too long, the fish may not be able to pass the culvert. See HEC 26 for more information on this topic.
Step 5. Determine Fish Passage Path Width
Finally, the available fish passage width, if any, is determined using the method and design charts described in this research report. If the width is insufficient, changing the culvert size, shape, slope, or other options should be evaluated to determine whether a feasible strategy for satisfying the design criteria exists.
Four design curves are available for a range of conditions as follows:
These design curves are shown graphically in figure 113 and in a tabular format in table 23. They are presented in a dimensionless format where the variables are defined as follows:
The design curves are applicable to circular, elliptical, pipe arch, and box shapes. The curves were developed for conditions where the flow top width, T, stays the same or increases with increasing water surface elevation. For box culverts, the top width remains the same for all water surface elevations. For circular, elliptical, and pipe arch shapes, the top width increases with increasing water surface elevation until the water surface elevation reaches the spring line of the culvert. Further increases in water surface elevation result in a decrease in flow top width. The design curves may only be used for water surface elevations above the spring line when the water surface top width has decreased 2 percent or less from the maximum top width.
Curve 4 is used for all box shapes.
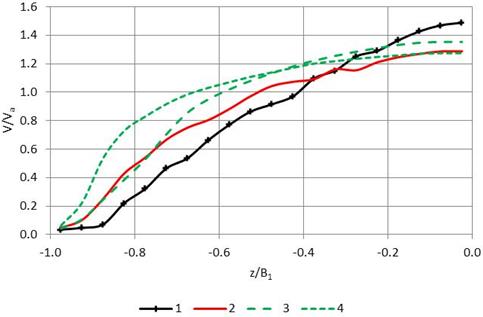
Figure 113. Graph. Vertical slice design curves
In addition to the limits on water surface elevation for circular, elliptical, and pipe arch culverts, these design curves are limited to the range of hydraulic conditions evaluated in the study. The Froude number, calculated based on the average depth and average velocity in the culvert, should be within the range of 0.1 to 0.5. It is also recommended that these curves only be applied to culverts with spans between 3 and 15 ft, inclusive.
Table 23. Tabular listing of vertical slice design curves.
Slice |
z/B1 |
V/Va |
V/Va |
V/Va |
V/Va |
|---|---|---|---|---|---|
1 |
-0.975 |
0.036 |
0.048 |
0.043 |
0.064 |
2 |
-0.925 |
0.047 |
0.103 |
0.108 |
0.225 |
3 |
-0.875 |
0.072 |
0.252 |
0.246 |
0.537 |
4 |
-0.825 |
0.221 |
0.430 |
0.386 |
0.729 |
5 |
-0.775 |
0.322 |
0.542 |
0.529 |
0.830 |
6 |
-0.725 |
0.465 |
0.667 |
0.705 |
0.917 |
7 |
-0.675 |
0.537 |
0.751 |
0.857 |
0.985 |
8 |
-0.625 |
0.666 |
0.806 |
0.951 |
1.032 |
9 |
-0.575 |
0.774 |
0.884 |
1.021 |
1.071 |
10 |
-0.525 |
0.865 |
0.974 |
1.081 |
1.108 |
11 |
-0.475 |
0.915 |
1.044 |
1.134 |
1.140 |
12 |
-0.425 |
0.972 |
1.073 |
1.182 |
1.172 |
13 |
-0.375 |
1.097 |
1.092 |
1.222 |
1.201 |
14 |
-0.325 |
1.153 |
1.160 |
1.256 |
1.218 |
15 |
-0.275 |
1.253 |
1.155 |
1.285 |
1.235 |
16 |
-0.225 |
1.291 |
1.211 |
1.310 |
1.248 |
17 |
-0.175 |
1.366 |
1.246 |
1.332 |
1.259 |
18 |
-0.125 |
1.428 |
1.269 |
1.348 |
1.270 |
19 |
-0.075 |
1.470 |
1.287 |
1.353 |
1.274 |
20 |
-0.025 |
1.488 |
1.287 |
1.353 |
1.274 |
Example computations for three situations are illustrated. The primary tools used in these examples are the design curves presented in this research report and HY-8 to calculate culvert characteristics.
Example 1. Embedded 6-ft Diameter CMP
For this example, a 6-ft diameter CMP with a length of 53 ft is considered. Using HEC 26 guidance, it is embedded 2 ft, the minimum recommended for a circular conduit. The stream bed material that will be placed in the culvert is a noncohesive material with a D50 of 0.944 inches and a D84 of 2.6 inches, which is the same material found in the stream. The tailwater channel is approximated by a trapezoidal channel with a bottom width of 5.5 ft and 1:1 side slopes. Both the culvert and the tailwater channel have a longitudinal slope of 0.15 percent.
Step 1. Estimate Design Flows
The high and low passage flows were determined to be 7.8 and 1.0 ft3/s, respectively, for this hypothetical location. See HEC 26 for more detailed discussion of the passage flows.
Step 2. Estimate Flow Depth and Composite Roughness
Manning's roughness for the culvert is obtained from HDS 5 for a CMP as 0.028. For the bed material, which is the same material in both the stream and within the culvert, Blodgett's equation is used. (See equation in figure 108.) Because the Manning's n for noncohesive bed materials is dependent on depth and depth is dependent on Manning's n, an iterative process is required. Considering the high passage discharge, a trial normal depth of 1 ft is assumed for the tailwater channel. Then, Manning's n is computed as follows (D50 is converted to units of feet):
n = 0.262y1/6/(2.25 + 5.23log(y/D50)) = 0.262(1)1/6/(2.25 + 5.23log(1/0.0786)) = 0.262/8.03 = 0.033
This n value is entered into HY-8 to represent both the tailwater and bed material Manning's n values. HY-8 is run, and the normal depth is given. This new normal depth is then entered into the Blodgett equation to compute a new Manning's n. This process is repeated until there are no further changes to Manning's n (within two significant figures). In this case, the normal depth was overestimated, but the Manning's n value does not change with the new depth. Therefore, a Manning's roughness value of 0.033 is used for the high passage flow.
The individual values for the culvert and bed material are entered into HY-8 for computation of composite roughness. For this case, the composite roughness is 0.032 for the high passage flow.
For the low passage flow, the same roughness value is used for the CMP, but the bed material value will increase because of the shallower depth. Using the same process, the Manning's roughness for the bed material is 0.041. Using HY-8, the composite value is 0.040.
Step 3. Compute Water Surface Top Width and Average Velocity
Using HY-8 for the high passage flow and the associated roughness value, the flow profile in the culvert is determined to vary from a depth of 0.88 ft at the culvert outlet to 0.89 ft at the culvert inlet. Therefore, the highest velocity in the culvert will occur at the outlet. From HY-8, that velocity is 1.51 ft/s.
The water surface top width is also needed and, for an embedded circular pipe, is computed from the equation in figure 111 with the support of the equation in figure 112. From the latter, the angle between a line to the water surface at the edge of the pipe from the center of the pipe to the vertical is calculated as:
θ = acos(1 - 2(ymax + de)/D) = acos(1 - 2(0.88 + 2.0)/6) = 87.7 degrees
The water surface top width T is calculated from:
T = D sing(θ) = 6 sin(87.7) = 5.995 ft
Because the total of the embedment and water surface depth brings the water surface close to the center of the culvert, the water surface top width is close to the culvert span for the high passage flow.
Using HY-8 for the low passage flow and the associated roughness value, the flow profile in the culvert is determined to be close to a constant 0.29 ft at the outlet and inlet. From HY-8, the velocity associated with that depth is 0.59 ft/s.
The water surface top width may be needed and is computed as before:
θ = acos(1 - 2(ymax + de)/D) = acos(1 - 2(0.29 + 2.0)/6) = 76.3 degrees
The water surface top width T is calculated from:
T = D sing(θ) = 6 sin(76.3) = 5.829 ft
Step 4. Find Appropriate Fish Swimming Characteristics
For the target fish species identified for this hypothetical case, the maximum velocity is 1.3 ft/s, and the minimum depth is 0.5 ft. At the low passage flow, the velocity meets the requirements for passage, but the depth of 0.29 ft does not. This is a common occurrence for the low passage flow. The recommended design approach to address this situation is to form a v-shaped channel within the culvert that provides the needed depth. See HEC 26 for more information.
Step 5. Determine Fish Passage Path Width
Given the average velocity of 1.51 ft/s under the high passage flow, it appears this culvert is a barrier to passage. The design charts of figure 113 and table 23 are used to determine whether a portion of the culvert includes velocities that are passable.
For the case of a circular culvert with an embedment of 33 percent (2 ft divided by 6 ft), design curve number 4 is appropriate. The ratio of the allowable fish velocity to the average velocity in the culvert is 1.3/1.51 = 0.86. For curve 4 in table 23, this value falls between the values for vertical slice 5 and vertical slice 6. Therefore, the leftmost five slices provide average velocities that are passable by the target fish.
Recall that each slice is one twentieth of one half of the water surface width (not the culvert span). As computed under step 3, the width, T, is 5.995 ft. Therefore, the fish passage width is 5 x (1/20) x (5.995/2) = 0.75 ft. Because this culvert is symmetrical, there is this same passage width on both the left and right edges of the culvert, with velocities sufficiently low that the target fish species can pass at the high passage flow.
The final check is whether there is sufficient depth for the target fish to pass. Inspection of the cross-section graphic in HY-8 shows that the depth is sufficient for passage throughout the estimated fish passage width. Therefore, the total fish passage width in the culvert for the target species is 1.5 ft, even though the average velocity in the culvert exceeds the allowable passage velocity.
Example 2. Embedded 8-ft Diameter CSP
For this example, an 8-ft diameter CSP with a length of 60 ft is considered. Using HEC 26 guidance, it is embedded 2.4 ft. (For circular culverts, 2 ft or 30 percent of the culvert diameter, whichever is larger, is recommended.) The stream bed material that will be placed in the culvert is a noncohesive material with a D50 of 2.36 inches and a D84 of 6.50 inches, which is the same material found in the stream. The tailwater channel is approximated by a trapezoidal channel with a bottom width of 7.5 ft and 1:1 side slopes. Both the culvert and the tailwater channel have a longitudinal slope of 0.5 percent.
Step 1. Estimate Design Flows
The high and low passage flows were determined to be 16.7 and 1.5 ft3/s, respectively, for this hypothetical location. See HEC 26 for more detailed discussion of the passage flows.
Step 2. Estimate Flow Depth and Composite Roughness
Manning's roughness for the culvert is obtained from HDS 5 for a CSP as 0.035. For the bed material, which is the same material in both the stream and within the culvert, Blodgett's equation is used. (See equation in figure 108.) Because the Manning's n for noncohesive bed materials is dependent on depth and depth is dependent on Manning's n, an iterative process is required. Considering the high passage discharge, a trial normal depth of 1 ft is assumed for the tailwater channel. Then, Manning's n is computed as follows (D50 is converted to units of feet):
n = 0.262y1/6/(2.25 + 5.23log(y/D50)) = 0.262(1)1/6/(2.25 + 5.23log(1/0.197)) = 0.262/5.94 = 0.044
This n value is entered into HY-8 to represent both the tailwater and bed material Manning's n values. HY-8 is run, and the normal depth is given. This new normal depth is then entered into the Blodgett equation to compute a new Manning's n. This process is repeated until there are no further changes to Manning's n (within two significant figures). In this case, the normal depth was slightly overestimated, but the Manning's n value does not change with the new depth. Therefore, a Manning's roughness value of 0.044 is used for the high passage flow.
The individual values for the culvert and bed material are entered into HY-8 for computation of composite roughness. For this case, the composite roughness is 0.042 for the high passage flow.
For the low passage flow, the same roughness value is used for the CMP, but the bed material value will increase because of the shallower depth. Using the same process, the Manning's roughness for the bed material is 0.067. Using HY-8, the composite value is 0.064.
Step 3. Compute Water Surface Top Width and Average Velocity
Using HY-8 for the high passage flow and the associated roughness value, the flow profile in the culvert is determined to vary from a depth of 0.96 ft at the culvert outlet to 0.99 ft at the culvert inlet. Therefore, the highest velocity in the culvert will occur at the culvert outlet. From HY-8, that velocity is 2.29 ft/s.
The water surface top width is also needed and, for an embedded circular pipe, is computed from the equation in figure 111 with the support of the equation in figure 112. From the latter, the angle between a line to the water surface at the edge of the pipe from the center of the pipe to the vertical is calculated as:
θ = acos(1 - 2(ymax + de)/D) = acos(1 - 2(0.29 + 2.4)/8) = 70.9 degrees
The water surface top width T is calculated from:
T = D sing(θ) = 8 sin(70.9) = 7.56 ft
Step 4. Find Appropriate Fish Swimming Characteristics
For the target fish species identified for this hypothetical case, the maximum velocity is 1.3 ft/s, and the minimum depth is 0.5 ft. At the low passage flow, the velocity meets the requirements for passage, but the depth of 0.29 ft does not. This is a common occurrence for the low passage flow. The recommended design approach to address this situation is to form a v-shaped channel within the culvert that provides the needed depth. See HEC 26 for more information.
Step 5. Determine Fish Passage Path Width
Given the average velocity of 2.29 ft/s under the high passage flow, it appears this culvert is a barrier to passage. The design charts of figure 113 and table 23 are used to determine whether a portion of the culvert includes velocities that are passable.
For the case of a circular culvert with an embedment of 30 percent (2.4 ft divided by 8 ft) design curve number 4 is appropriate. The ratio of the allowable fish velocity to the average velocity in the culvert is 1.3/2.29 = 0.57. For curve 4 in table 23, this value falls between the values for vertical slice 3 and vertical slice 4. Therefore, the leftmost three slices provide average velocities that are passable by the target fish.
Recall that each slice is one twentieth of one half of the water surface width (not the culvert span). As computed under step 3, the width, T, is 7.90 ft. Therefore, the fish passage width is 3 x (1/20) x (7.90/2) = 0.59 ft. Because this culvert is symmetrical, there is this same passage width on both the left and right edges of the culvert, with velocities sufficiently low that the target fish species can pass at the high passage flow.
The final check is whether there is sufficient depth for the target fish to pass. Inspection of the cross-section graphic in HY-8 shows that the depth is sufficient for passage throughout the estimated fish passage width. Therefore, the total fish passage width in the culvert for the target species is 1.18 ft, even though the average velocity in the culvert exceeds the allowable passage velocity.
Example 3. Embedded 8 ft x 8 ft Concrete Box Culvert
For this example, an 8- x 8-ft concrete box culvert (CBC) with a length of 60 ft is considered. Using HEC 26 guidance, it is embedded 2 ft, the minimum recommended for a box culvert. The stream bed material that will be placed in the culvert is a noncohesive material with a D50 of 2.36 inches and a D84 of 6.50 inches, which is the same material found in the stream. The tailwater channel is approximated by a trapezoidal channel with a bottom width of 7.5 ft and 1:1 side slopes. Both the culvert and the tailwater channel have a longitudinal slope of 0.5 percent.
Step 1. Estimate Design Flows
The high and low passage flows were determined to be 16.7 and 1.5 ft3/s, respectively, for this hypothetical location. See HEC 26 for more detailed discussion of the passage flows.
Step 2. Estimate Flow Depth and Composite Roughness
Manning's roughness for the culvert is obtained from HDS 5 for a CBC as 0.014. For the bed material, which is the same material in both the stream and within the culvert, Blodgett's equation is used. (See equation in figure 108.) Because the Manning's n for noncohesive bed materials is dependent on depth and depth is dependent on Manning's n, an iterative process is required. Considering the high passage discharge, a trial normal depth of 1 ft is assumed for the tailwater channel. Then Manning's n is computed as follows (D50 is converted to units of feet):
n = 0.262y1/6/(2.25 + 5.23log(y/D50)) = 0.262(1)1/6/(2.25 + 5.23log(1/0.197)) = 0.262/5.94 = 0.044
This n value is entered into HY-8 to represent both the tailwater and bed material Manning's n values. HY-8 is run, and the normal depth is given. This new normal depth is then entered into the Blodgett equation to compute a new Manning's n. This process is repeated until there are no further changes to Manning's n (within two significant figures). In this case, the normal depth was overestimated, but the Manning's n value does not change with the new depth. Therefore, a Manning's roughness value of 0.044 is used for the high passage flow.
The individual values for the culvert and bed material are entered into HY-8 for computation of composite roughness. For this case, the composite roughness is 0.039 for the high passage flow.
For the low passage flow, the same roughness value is used for the CMP, but the bed material value will increase because of the shallower depth. Using the same process, the Manning's roughness for the bed material is 0.067. Using HY-8, the composite value is 0.064.
Step 3. Compute Water Surface Top Width and Average Velocity
Using HY-8 for the high passage flow and the associated roughness value, the flow profile in the culvert is determined to vary from a depth of 0.96 ft at the outlet to 0.94 ft at the inlet. Therefore, the highest velocity in the culvert will occur at the inlet. From HY-8, that velocity is 2.21 ft/s.
The water surface top width for a box culvert is always the span of the culvert, which in this case is 8 ft.
Using HY-8 for the low passage flow and the associated roughness value, the flow profile in the culvert is determined to be 0.29 ft at the outlet and 0.28 ft at the inlet. From HY-8, the velocity associated with that depth is 0.67 ft/s.
The water surface top width may be needed and is 8 ft, as it was for the high passage flow.
Step 4. Find Appropriate Fish Swimming Characteristics
For the target fish species identified for this hypothetical case, the maximum velocity is 1.3 ft/s, and the minimum depth is 0.5 ft. At the low passage flow, the velocity meets the requirements for passage, but the depth of 0.28 ft does not. This is a common occurrence for the low passage flow. The recommended design approach to address this situation is to form a v-shaped channel within the culvert that provides the needed depth. See HEC 26 for more information.
Step 5. Determine Fish Passage Path Width
Given the average velocity of 2.21 ft/s under the high passage flow, it appears this culvert is a barrier to passage. For all box culverts, design curve 4 from figure 113 and table 23 is used to determine whether a portion of the culvert includes velocities that are passable.
The ratio of the allowable fish velocity to the average velocity in the culvert is 1.3/2.21 = 0.59. For curve 4 in table 23, this value falls between the values for vertical slice 3 and vertical slice 4. Therefore, the leftmost three slices provide average velocities that are passable by the target fish.
Recall that each slice is one twentieth of one half of the water surface width. As computed under step 3, the width, T, is 8.0 ft. Therefore, the fish passage width is 3 x (1/20) x (8/2) = 0.60 ft. Because this culvert is symmetrical, there is this same passage width on both the left and right edges of the culvert, with velocities sufficiently low that the target fish species can pass at the high passage flow.
The final check is whether there is sufficient depth for the target fish to pass. Because the depth is constant across the entire span, the depth is sufficient for passage throughout the estimated fish passage width. Therefore, the total fish passage width in the culvert for the target species is 1.2 ft, even though the average velocity in the culvert exceeds the allowable passage velocity.