U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-013 Date: February 2017 |
Publication Number: FHWA-HRT-17-013 Date: February 2017 |
One objective of this research study was to provide guidance for riprap apron design for vertical-wall abutments on shallow foundations. The resulting guidance covers several topics: (1)flush riprap aprons, (2) buried riprap aprons, (3)geometric parameters for irregular channel shapes, and (4)implications of contraction ratio. This guidance applies to all vertical-wall abutment designs with shallow foundations, including GRS bridge abutments.
Under existing HEC-23 DG14 guidance, riprap aprons installed flush with the streambed to protect against abutment scour should extend out from the abutment a distance of two times the pre-scour depth of flow in the contraction or 25 ft (7.6 m), whichever is smaller.(3) This extension may leave a gap in protection across the channel that may result in contraction scour deeper than anticipated, which may ultimately increase the movement of rocks at the edges of the riprap apron (edge failure).
A buried full-width apron was proposed to address the concern regarding edge failure. Physical modeling of various apron configurations was conducted to evaluate a buried full-width apron. A buried partial-width installation was also evaluated with CFD modeling runs. In the following sections, the recommended applicability and limits for riprap aprons are provided.
Based on the conceptual analysis and experimental tests of riprap aprons installed flush with the original bed surface conducted for this study, the shear ratio, τR / τB, decreased as the relative width of the contraction increased. This conceptual relation is shown by the curve in figure 95. One would expect that in the extreme, (i.e., is when the opening is very wide), a limited width riprap apron would have little influence on the flow condition in the contraction and the shear ratio would approach 1.0. However, when the opening is narrow, the riprap would have an effect on the flow distribution and would cause the shear ratio to increase. A higher shear ratio indicated deeper contraction scour in the gap between the abutment aprons than would otherwise be expected. Therefore, as indicated by the question mark on the figure, “narrow” must be quantified for this application.
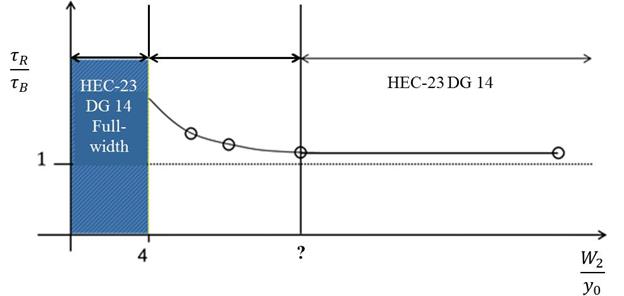 |
| Figure 95. Graph. Conceptual definition of a narrow opening for flush apron installation. |
Because HEC-23 DG14 recommends aprons equal to two times the pre-scour flow depth, y0, contractions with an opening ratio, W2/y0, less than or equal to 4 (considering the apron from both abutments) are essentially full-width aprons.(3) Above a certain opening ratio, indicated in figure 95, HEC-23 DG14 may also be applied because the channel is sufficiently wide so that the localized effect of the riprap on the contraction scour and apron edges is negligible. This corresponds to where the shear ratio, τR / τB, is close to 1. One of the objectives of this study was to address guidance for the region between the two extremes.
As reported in the discussion of the CFD modeling results in chapter 5, shear ratios ranging from 1.03 up to 2.56 were computed over the 30 flush installation cases analyzed. These cases used different riprap and bed material sizes over a range of opening ratios from 6.2 to 16. However, it was noted that other variables also influenced the shear ratio.
A strategy for identifying an appropriate threshold was adapted from a procedure used for the seismic design of bridges. The California Department of Transportation proposed that a realistic moment-curvature curve could be approximated by considering idealized plastic behavior to estimate the plastic moment capacity of a ductile concrete structural section, as shown in figure 96.(24) The actual elastic structural behavior was approximated, identifying the intersection point between the idealized plastic behavior and a secant line representing the elastic modulus.
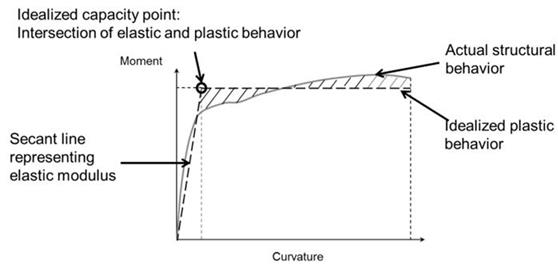 |
| Figure 96. Graph. Idealized elastic perfectly plastic moment curvature. |
Similarly, if a secant line can be identified that intersects the ideal bed shear ratio of 1.0 at a consistent ratio of W2/y0, this may be an appropriate technique for defining a threshold for a narrow opening. A secant line was defined by the two points at which it intersected the curve; therefore, each curve had many secant lines. For this analysis, one secant definition point was taken where W2/y0 was equal to 4 because this was the point at which the aprons would be full width by HEC-23 DG 14 as was shown in figure 95.(3) Ideally, the second point should be chosen so that the intersection of the secant line and the ideal shear ratio of 1.0 occurred at a consistent W2/y0 ratio for a family of curves. One option was to take the second point where W2/y0 was equal to 6 because this value would work reasonably well for the CFD data.
Figure 97 shows the result of applying secant definition points of 4 and 6 for three groups of experiments included in table 4. Using the secant method for these curves yielded a threshold value of approximately 8. However, at this opening ratio, the shear ratio ranged from 1.4 to 1.8. These shear ratios were not approaching 1.0 at this opening ratio. It should be noted that the shear ratio corresponding to an opening ratio of 4.0 was extrapolated using the fitted curves beyond the CFD experimental range, which had a lower limit of 6.2.
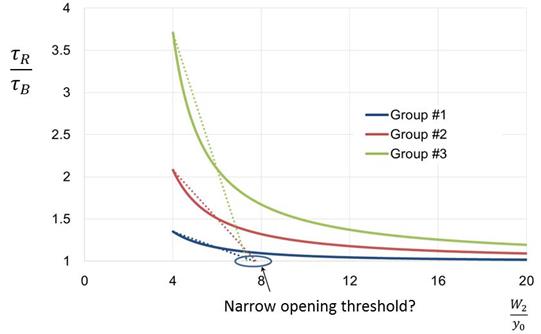 |
| Figure 97. Graph. Secant approach applied to selected CFD modeling cases. |
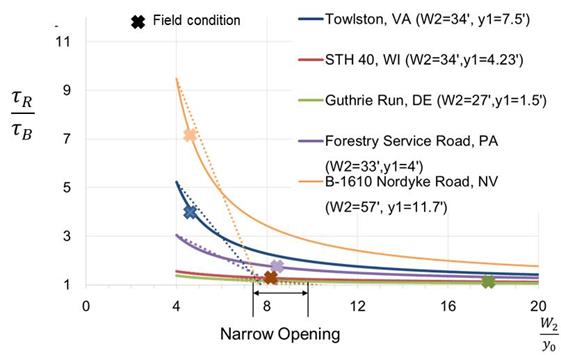
Data from five field sites were also examined using the secant method, as summarized in figure 98. The geometric and hydraulic characteristics of each site were entered into the equation in figure 55 to compute the shear ratio. These points are shown in the figure as the field condition. Then, the value of W2/y0 was varied to develop the curves for each site. The result when applying the secant approach suggests a threshold value between 7.5 and 8.0. As with the CFD results, the shear ratios for some of these sites at these opening ratios were well above 1.0.
 1 ft = 0.305 m. |
| Figure 98. Graph. Secant approach applied to field installation cases. |
The results of the secant approach depended on the points used to define the secant. Selecting 4 and 6 appeared to result in a reasonably consistent intersection with the shear ratio of 1.0 at W2/y0 equal to approximately 8. Choosing 4 and a higher value than 6 for the second secant definition point would result in a higher, but less consistent, ratio of W2/y0, where the secant lines intersected the shear ratio of 1.0. However, it is important that although the intersection point was consistent with secant definition points of 4 and 6, the shear ratios where W2/y0 equals 8were not close to 1.0.
Another approach for defining when full-width protection is recommended for flush installations of riprap aprons would be to use the equation in figure 55. If the result of the computation were greater than some value, say 1.3, then full-width protection would be recommended. However, this equation is not operational for design because it had not been comprehensively evaluated at the time of this study. In addition, methods for estimating some of the parameters, such as the channel shape factors, βB and βe, were not yet available. However, the potential for this approach is that it explicitly includes all input variables believed to be contributing to the increase in shear stress in the middle of the channel.
Based on inspection of the laboratory and field results as partially summarized in figure 97 and figure 98, respectively, partial-width riprap aprons installed flush with the bed surface would not be recommended because the shear ratio does not approach 1 except for larger ratios of W2/y0. Full-width installations might be acceptable from a scour perspective, but unacceptable for environmental or other reasons. If a full-width riprap apron installed flush with the bed is considered, other aspects of the apron design, including rock size, use of geotextile, and upstream and downstream extent, should be taken from HEC-23 DG14.(3) As much as possible, the riprap apron should conform to the stream channel and bank geometry.
Physical experimental runs 6, 8, 9, and 11 described in chapter 4 explored the performance of full-width riprap aprons buried so that the top of the apron layer matched the estimated contraction scour depth for the bridge opening. In each of these runs, the rock size was selected based on HEC-23 DG 14 for abutment aprons flush with the original bed elevation.(3) In none of these runs was any failure of the buried full-width apron observed.
In all of these runs, some of the bed material above the buried apron was removed before any part of the apron was exposed to shear stresses or potential undermining at the upstream and downstream apron edges. This expansion of the bridge opening cross section increased the conveyance through the opening and decreased the shear stresses on the riprap compared with what would have been experienced if the apron had been installed at a higher elevation.
Therefore, it is anticipated that burying the apron would allow for a reduction in the apron extent and rock sizing. For example, apron extent for HEC-23 DG 14 is 2y0, which potentially might be reduced with a buried apron.(3)
The CFD results from group 7 (cases 31–35) suggested that burying the riprap apron reduced the shear ratio because the apron itself no longer prevented the contraction scour from occurring, which in turn allowed the conveyance to increase and the bed shear to decrease. Review of the shear summaries for these cases in figure 114 (see appendix C), shows that the shear stresses in the unprotected part of the channel in the cases with riprap were equivalent to or lower than the stresses in the same area for the cases without riprap. In addition, the riprap apron protected the areas showing elevated shear stresses that would cause the local abutment scour. These cases included evaluations for the ratio of W2/y0 from 6.2 to 16. Therefore, a buried installation with a riprap apron extent of at least 2y0 from the abutment face toward the channel thalweg could be protective of the abutment foundation for W2/y0 greater than 6.2. Such an installation might also be protective for narrower channel constrictions, but no data to support this conclusion was developed as part of this study.
The physical and numerical modeling for this study, as well as the conceptual framework, primarily applied to rectangular and trapezoidal channels. Because designers and engineers must apply these concepts to irregularly shaped natural channels, clarity regarding the definition of the hydraulic and channel parameters is essential.
First, all analyses assumed that all flow approaching a bridge opening passed through the opening; there was no overtopping or bypass. For situations where overtopping and bypass would occur, the upstream flow, velocity, depth, and width should be estimated considering only that portion of the flow field that was directed through the bridge opening.
In the analyses for this study, the widths of the upstream and contracted section, W1 and W2, respectively, were defined as the bottom width of the section. Because bottom width is difficult to define in an irregular channel, and the bottom width and average width are were the same in the rectangular channel used in the physical experiments, the recommendation is to use average width for characterizing contraction ratio and other width-related parameters for irregular channels. Average width is defined in figure 99 for the upstream section. The analogous relation is used for the contracted section.
![]()
Figure 99. Equation. Average width in the approach section.
Where:
![]() 1 = Average width in upstream section, ft (m).
1 = Average width in upstream section, ft (m).
A1 = Cross-sectional area of upstream section, ft2 (m2).
y1M = Maximum flow depth in the upstream section, ft (m).
For depth, the average flow depths in the upstream and contracted sections (before and after contraction scour), y1, y0, and y2, respectively, were defined for these analyses. For a rectangular channel, the average and maximum depths were the same. For irregular channels, it is recommended that the average depth is appropriate for estimating full-width apron design parameters. The exception is that the depth at the abutment, as defined in HEC-23 DG14, should be used for rock sizing.(3)
Velocity and cross-sectional area parameters should be defined based on the entire upstream and contracted section. The exception would be when flow overtops or bypasses the bridge opening.
Channel contraction at bridge openings may create hydraulic and scour challenges as well as environmental and ecosystem effects. With respect to the shear stress ratio described in this study, greater contraction resulted in greater flow acceleration through the bridge opening. Greater contraction (lower contraction ratio) also led to higher estimates of contraction scour and larger rock riprap sizes to protect abutments from abutment scour. For partial-width aprons, these effects would likely result in higher stresses in the gap between the aprons.
The physical modeling in this study tested two contraction ratios (W2/W1): 0.65 and 0.25. For the more severe 0.25 contraction ratio, the observed contraction scour depths for the two runs without riprap protection were twice the estimated values. While these estimates should not be directly compared for the reasons discussed in chapter 4, they are indicative of a severe environment.
The numerical CFD modeling tested less severe contraction ratios ranging from 0.72 to 0.90. As discussed in chapter 5, the shear ratios exceeded 2.0 in some cases depending on riprap size, opening ratio, and other factors.
The equation in figure 55 implicitly includes contraction to estimate shear ratio. Until more experience is gained with this equation and with vertical-wall abutments with shallow foundations, it is recommended to carefully consider contraction ratio in the design. More severe contractions contribute to a more challenging hydraulic and scour environment. Lower contraction ratios (more contraction) increase contraction scour estimates, which lead to deeper riprap aprons when buried to the contraction scour depth.