U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-11-056 Date: October 2012 |
Publication Number: FHWA-HRT-11-056 Date: October 2012 |
This section provides a brief review of the computer vision technologies that were used in this project, and it discusses recent work in vision-based pedestrian detection.
The key vision technologies used as background technology in this project include the following:
Stereo vision is a process of triangulation that determines range from two images taken from two different positions. These two images are taken simultaneously from a pair of cameras with a known baseline (i.e., separation distance between the cameras). In this implementation, the research team designed the camera setup so that the optical axes of the two cameras were almost parallel. The objective of a stereo vision system is to find correspondences in the images captured by the two cameras. This is usually done by some manner of image correlation and peak finding. The image correlation function is a local correlation-based method that provides a dense disparity map of the image, which can then be converted to a range map. The correlation function implemented is the sum of absolute differences (SAD). The equation for SAD for each pixel in an image when computed over a 7 × 7 pixel local region is found in figure 1.
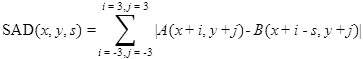
Figure 1. Equation. SAD.
Where:
A = Left image of the stereo pair.
B = Right image of the stereo pair.
x and y = Image pixel locations.
s = Number of horizontal shifts that are searched to find an image correlation.
There are other functions that could be used for local image correlation, including the sum of squared differences and normalized correlation. After the correlation was computed, 32 horizontal shifts in this case, the minimum value was detected and interpolated for an accurate disparity estimate. In this implementation, the SAD correlation was applied to multiple resolutions of the image pair, extending the search range by a factor of two for every coarser resolution image. The disparity estimates obtained at coarser resolutions are generally less prone to false matches that can occur in regions of low texture, but they are commensurately less accurate.
The computed disparity maps based on these methods are often noisy because the range of data depends on accurately correlating each point in the image to a corresponding point in the other image. To increase the reliability of the range data, the image can be prefiltered (with boxcar or Gaussian filters), and the summing window for SAD can be changed from 7 × 7 pixels to 13 × 7 pixels. Additionally, the researchers masked out potentially unreliable data by computing a local texture measure and comparing it to a threshold. Researchers also compared the disparity estimates between the right image referenced to the left and the left image referenced to the right, checking for consistency between the two results. This checking method masks inconsistent or ambiguous disparity data such as areas that are occluded by one of the two cameras. Disparity maps computed at multiple resolutions are combined before range (depth) is computed.
Given the horizontal coordinates of corresponding pixels, xl and xr, in the left and right image, the range, z,can be expressed as follows:
![]()
Figure 2. Equation. The range estimate of an image pixel.
Where:
b = The stereo camera baseline.
f = The focal length of the camera in pixels.
d = The image disparity value.
HOG is a method of encoding and matching image patches under varying image orientation and scale changes. It is defined as the HOG directions of image pixels within a rectangular sampling window on an image. The gradient direction of each pixel in an image can be computed by convolving it with the Sobel mask (or differential kernels) in the X and Y directions. The ratio of convolution along two directions gives the underlying image feature direction. The gradient direction of each pixel is then binned in nine directions covering 180 degrees. HOG is then computed by gathering the directions of pixels inside a sampling window and weighting each response by the edge strength. This results in an 8 × 1 vector that is then normalized to be bound in a [0, 1] range. Figure 3 shows an illustration of how a HOG is computed. The image location is shown in blue in the photo of the pedestrian.
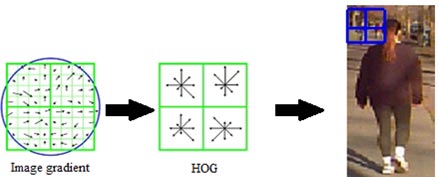
Figure 3. Illustration. HOG computed at an image location.
Within small regions, HOG encodes dominant shapes, which are computed by a voting scheme applied to the region’s edge segments (see figure 4). Specifically, an image patch or region is first subdivided into multiple image cell regions. Each cell region is further divided into 2 × 2-pixel or 3 × 3-pixel local grids. The HOG feature is computed for each local grid region. For pedestrian recognition, candidate image patches are typically resized to a nominal size of 64 × 128 pixels, and HOG is computed. To handle image noise and exploit pedestrian shape, the algorithm applies a four-tap Gaussian filter to smooth the image and enhances it using histogram stretching.
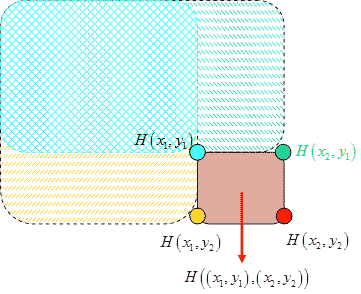
Figure 4. Illustration. HOG computation using integral images.
To efficiently compute HOG for use in a real-time system, an integral image is pre-computed so that HOG can be retrieved by look-up operations that consist of simple arithmetic summations. The integral image denotes a stack of image encoding where cumulative histogram of orientation for each pixel is computed by a fast scanning method. The integral histogram is computed as follows:
![]()
Figure 5. Equation. Computation of integral histogram.
Given a candidate pedestrian region of interest (ROI), the corresponding HOG for each ROI is computed by sampling integral histogram as follows:
![]()
Figure 6. Equation. Computation of HOG for a specific image patch.
This project uses the AdaBoost classifier algorithm for multi-object recognition. The AdaBoost algorithm was introduced in 1995 by Freund and Schapire, and a tutorial is provided by Friedman et al.(3,4) Classifiers are supervised machine-learning procedures in which input test data are assigned to one of N labels based on a model that was learned from a representative training dataset. AdaBoost uses a training set (x1, y1)… … …(xm, ym) where xi belongs to a domain X and yi is a label in some label set Y. For simplicity, assume the labels are -1 or +1. AdaBoost calls a given weak learning algorithm repeatedly. It maintains a distribution or set of weights over the training set. Initially, all weights are set equally, but on each round, the weights of incorrectly classified examples are increased so that the weak learner is forced to focus on harder examples in the training set. The goodness of a weak hypothesis is measured by its error; this error is measured with respect to the distribution on which the weak learner was trained. The following information provides the pseudo-code for the algorithm:
Given (x1, y1)… … …(xm, ym) where xi ∈ X, yi ∈ Y = {-1, +1}:
Initialize D1(i) = 1/m
For t = 1, … …, T, use the following:
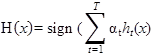
One of the key contributions from this project was the development of a principled method to label scene structure into buildings, trees, other tall vertical structures (e.g., poles), and objects of interest (e.g., pedestrians and vehicles). This approach relied on posing the labeling problem as Bayesian labeling in which the solution is defined as the maximum a posteriori (MAP) probability estimate of the true labeling. This posterior is usually derived from a prior model and a likelihood model, which, in turn, depends on how prior constraints are expressed. The MRF theory encodes contextual constraints into the prior probability. MRF modeling can be performed in a systematic way as follows:
A more detailed treatment of MRF models in computer vision is provided in Markov Random Fields and Their Applications.(5)
One of the most popular recent pedestrian detection algorithms is the HOG method created by Dalal and Triggs.(6) They characterized pedestrian regions in an image using HOG descriptors, which are a variant of the well-known scale invariant feature transform (SIFT) descriptor.(7) Unlike SIFT, which is sparse, the HOG descriptor offers a denser representation of an image region by tessellating it into cells which are further grouped into overlapping blocks. At each cell, a HOG at pixels belonging to the cell is computed. Within each block, a HOG descriptor is calculated by concatenating individual cell histograms belonging to that block and normalizing the resulting feature vector to give some degree of illumination invariance. A two-class support vector machine (SVM) classifier was trained using the HOG features and used for final pedestrian detection.
Dalal and Triggs reported significantly better results compared to previous approaches based on wavelets and a principle component analysis SIFT of around 90 percent correct pedestrian detection at 10-4 FPs per number of windows (FPPW) evaluated.(6, 8, 9) Note that based on the image size and the number of scales used to detect pedestrians, a FP rate of 10-4 FPPW corresponds to about 0.4 FPs per frame (FPPF).
Tuzel et al. proposed the covariance descriptor to characterize global image regions and used a Riemannian manifold for pedestrian detection.(10) They reported improved results of about 93.2 percent correct detection compared to the HOG descriptor at the same rate of 10-4 FPPW. Tran and Forsyth used geometric features describing the spatial layout of parts with appearance features characterizing individual parts.(11) They employed structured learning to determine the discriminative configuration of parts and reported excellent detection rates exceeding 95 percent with 0.1 FPPF (10-4 FPPW naive Bayes weight) less number of window needed to be evaluated since the approach is robust to centering of the pedestrian ROI) on the INRIA Person Dataset, though no time performance was discussed.(12) Wu and Nevatia used a cluster boosted tree classifier for pedestrian detection and also showed a performance of 95 percent at 10-4 FPPW.(13)
Leibe et al. described a stereo-based system for three-dimensional (3D) dynamic scene analysis from a moving platform, which integrates a sparse 3D structure estimation with multicue image-based descriptors (shape context) computed using Harris-Laplace and HOG features to detect pedestrians.(14, 15) The authors showed that the use of sparse 3D structure significantly improved the performance of pedestrian detection. The best performance cited was 40 percent probability of detection at 1.65 FPPF. While the structure estimation was performed in real time, the pedestrian detection was significantly slower.
Gavrila and Munder proposed Preventive Safety for Unprotected Road User (PROTECTOR), a real-time stereo system for pedestrian detection and tracking.(16) PROTECTOR employs sparse stereo and temporal consistency to increase the reliability and mitigate misses. Gavrila and Munder reported 71 percent pedestrian detection performance at 0.1 FPPF without using a temporal constraint with pedestrians located less than 82 ft (25 m) from the cameras. However, the datasets used were from relatively sparse, uncluttered environments. Recently, Doll´ar et al. introduced a new pedestrian dataset and benchmarked a number of existing approaches.(17)
Another leading real-time monocular vision system for pedestrian detection was proposed by Shashua et al.(18) A focus of attention mechanism was used to rapidly detect candidates. The window candidates (approximately 70 per frame) were classified as pedestrians or nonpedestrians using a two-stage classifier. Each input window was divided in 13 image subregions. At each region, a histogram of image gradients was computed and used to train an SVM classifier. The training data were divided into nine mutually exclusive clusters to account for pose changes in the human body. The 13 × 9 vector containing the response of the SVM classifiers for each of the nine training clusters were used to train, as well as AdaBoost second-stage classifier. A practical pedestrian awareness system requires few FPs per hour of driving. As a result, the authors employed temporal information to improve the per-frame pedestrian detection performance and to separate in-path and out-of-path pedestrian detections, which increased the latent period in the system.
Hoeim et al. presented a method for learning 3D context from a single image by using appearance cues to infer simple geometric labelings.(19) Hoiem et al. also presented a probabilistic detection framework which exploits the overall 3D context extracted using Geometric Context from a Single Image.(19) The authors argued that object recognition could not be solved locally but required statistical reasoning over the whole image.(20)
Wojek and Schiele proposed a probabilistically sound combination of scene labeling and object detection using a conditional random field, but their method relied on appearance rather than 3D.(21) Brostow et al. investigated the use of 3D features from structure-from-motion to classify patches in the scene.(22)