U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
| Publication Number: FHWA-HRT-12-030 Date: August 2012 |
Publication Number: FHWA-HRT-12-030 Date: August 2012 |
PDF Version (4.44 MB)
PDF files can be viewed with the Acrobat® Reader®
A key requirement in conducting M-E design or analysis of pavements is to estimate stresses, strains, and deflections within unbound base, subbase, embankment, and subgrade layers. The critical stresses, strains, and deflections are then used in empirical models to forecast future pavement conditions. Mostly, critical stresses, strains, and deflections within all pavement layers (including unbound base, subbase, embankment, and subgrade layers) are determined using finite element analysis (FEA) or layered elastic analysis (LEA). A key input required for determining critical stresses, strains, and deflections using LEA or FEA techniques is unbound layer material resilient modulus.
Resilient modulus is a dynamic response of
unbound layer materials to continuous dynamic loading of a pavement
by vehicles. It is defined as the ratio of the repeated axial
deviator stress to the recoverable axial strain and is determined
in the laboratory by means of a triaxial testing. Because resilient
modulus is sensitive to the stress state the unbound material is
subjected to (combination of confining stress (![]() ) and deviator stress (
) and deviator stress (![]() )), testing typically is done over a range of
confining and deviator stresses. A mathematical model is then
fitted to the resilient modulus and confining and deviator stress
data for use in estimating resilient modulus for any reasonable
combination of confining and deviator stresses.
)), testing typically is done over a range of
confining and deviator stresses. A mathematical model is then
fitted to the resilient modulus and confining and deviator stress
data for use in estimating resilient modulus for any reasonable
combination of confining and deviator stresses.
Developing correlations between resilient modulus and basic unbound granular/coarse-grained and fine-grained materials for use in pavement analysis and design was one of the objectives of this study. As with the other models described in this report, the LTPP database contained adequate data to develop a resilient modulus model for unbound materials.
The literature review included several models developed for the use in predicting resilient modulus using unbound material index properties. From this literature review, a list was developed of all unbound material properties that impact resilient modulus and thus could potentially be included in a resilient modulus prediction model.
Unbound material properties of interest, along with resilient modulus data required for model development as determined through the literature review, were obtained from the LTPP database and assembled in a model development database. Also included in this database were actual resilient modulus test results and the range of confining and deviator stresses at which resilient modulus was determined.
Individual LTPP material database tables were merged to develop the resilient modulus model development database. Because the LTPP database is a relational database (i.e., it is composed of separate but related data tables), data assembly was performed by linking data stored in a simple row/column format in tables using unique primary keys to identify LTPP test sections or projects. For many of the data tables, the primary keys were the combination of STATE_CODE, SHRP_ID, and CONSTRUCTION_NO.
The next step was to determine the AASHTO soil classification for each unbound material of the database. The gradation and Atterberg limits were used to determine the soil classification.
The assembled data were reviewed thoroughly to identify anomalies and missing data elements, as well as to assess the reasonableness of the data. While this review was performed for all models developed, the review was more in-depth for the resilient modulus data because of the sheer size of the database and because of the potential for large model errors for relatively small data discrepancies.
Examples of plots summarizing the assembled data used to assess data reasonableness are presented in figure 235 through figure 247. The data were assembled and reviewed by each AASHTO soil class to assess if the trends in the data were reasonable.
The following conclusions were made based on the review of assembled data:
The following anomalies were identified when matching material properties data elements to Mr data for subgrade soils:
Over half the test sections did not have all the data elements (e.g., hydraulic conductivity) required to fully characterize the pavement subgrade. However, sufficient data were available for key subgrade material properties (e.g., gradation and Atterberg limits). Data elements for which little data were available were not used in model development.
A significant anomaly was differences in subgrade soil materials used for different types of testing due to sampling location. This anomaly was resolved by matching resilient modulus data to other soil test data only when the sample location could be certified as being as close as possible (i.e., same depth/strata, same test pit, etc.).
A second anomaly was the lack of a single representative resilient modulus value for a given unbound material sample (i.e., series of resilient modulus values corresponding to a combination of deviator and confining stresses used during testing process). This situation has been resolved in the past by fitting the series of resilient modulus values corresponding to a combination of deviator and confining stresses used during testing process with a constitutive equation that models resilient modulus behavior for both granular and fine-grained materials.
As defined in chapter 3, the AASHTO Mechanistic-Empirical Pavement Design Guide, Interim Edition: A Manual of Practice proposes the constitutive equation for modeling resilient modulus behavior when subjected to various stress states the following:(1)
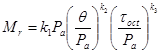
Where:
![]() = Bulk stress =
= Bulk stress = ![]() .
.
![]() = Principal stress.
= Principal stress.
![]() = Confining
pressure.
= Confining
pressure.
Pa = Atmospheric pressure.
![]() = Octahedral
normal stress = 1/3 (
= Octahedral
normal stress = 1/3 (![]() ).
).
k1, k2, k3 = Regression constants that are a function of soil properties, as defined in figure 75, through figure 77.
This model can be used for various soil types, and the model attributes (k1, k2, and k3) for a given soil type remain the same regardless of stress state. Developing models to predict constitutive model attributes for a given set of soil properties is thus an effective approach to modeling resilient modulus behavior, rather than developing models individually for each possible combination of expected stress states.
Figure 33 presents the constitutive equation that models resilient modulus behavior for both granular and fine-grained materials recommended by the AASHTO Mechanistic-Empirical Pavement Design Guide, Interim Edition: A Manual of Practice.(1) The parameters k1, k2, and k3 were calculated for all datasets based on the soil properties. Histograms showing the distribution of k1, k2, and k3 values by soil class are shown in figure 249 through figure 251, respectively.
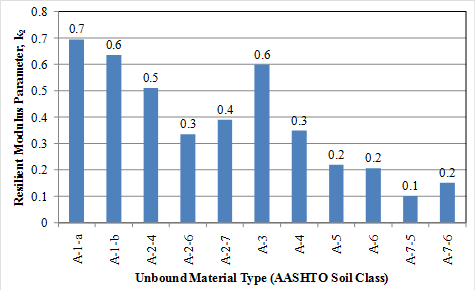
This model was fitted to all soil samples with resilient modulus available for a range of confining and deviator stresses. Model fitting was done individually for each unbound material sample in the LTPP database. For each of the soil samples, calculated k1, k2, and k3 and the constitutive equation were used to predict resilient modulus at the lab test confining and deviator stresses for comparison. The results of the comparison showed a good fit of predicted and measured resilient modulus with a high R2 value and low standard error of estimate (SEE), as presented in figure 252.
The following five-step procedure using regression analysis was used to develop multiple linear regression models relating resilient modulus to unbound material properties:
Details of the procedure are explained in the following sections.
Various forms of mathematical relationships have been used for relating constitutive model parameters k1, k2, and k3 to simple material properties. The two most commonly applied, and hence most promising, model forms are as follows:
Where ki is k1, k2, and k3. Because both of these mathematical equations have been used successfully, they were both deemed appropriate and were adopted for model fitting in this project.
The data assembled contained all inputs required for model development. Details are as previously described.
Numerous preliminary multivariable regression runs were performed to produce the “best” model. The goal was to determine the optimal set of independent variables (material properties) that, when included in the model, will maximize adjusted R2 values and minimize errors (SEE). Other diagnostic statistics, such as the level of significance of the regression coefficient of each independent variable, COLLIN (used to check for multicollinearity) in SAS®, and VIF were made to determine the goodness of fit for the model.
Independent variables with regression coefficients significant at the 0.05 significance level (determined through performing t-tests) were retained in the models developed. The t-test threshold was set at this level so that only variables that impacted k1, k2, and k3 were significantly included in the models. The resulting models developed through regression analysis for constitutive model parameters k1, k2, and k3 are described below.
Constitutive Model Parameter k1:
Model statistics for k1 are as follows:
Constitutive Model Parameter k2:
Model statistics for k2 are as follows:
Constitutive Model Parameter k3:
Where:
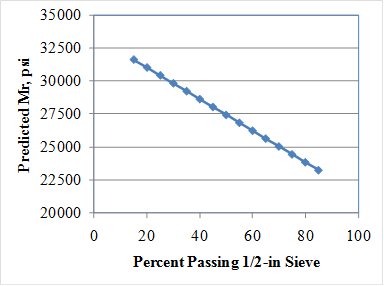
PCTHALF = Percent passing 1/2-inch sieve.
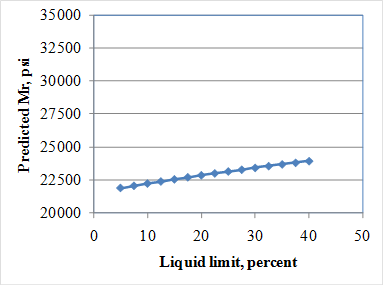
LL = Liquid limit, percent.
OPTMOIST = Optimum moisture content, percent.
PCTNO80 = Percent passing No. 80 sieve.
PCTGRVL = Percent gravel fraction (0.078- to 2.36-inch size).
D10 = Maximum particle size of the smallest 10 percent of soil sample.
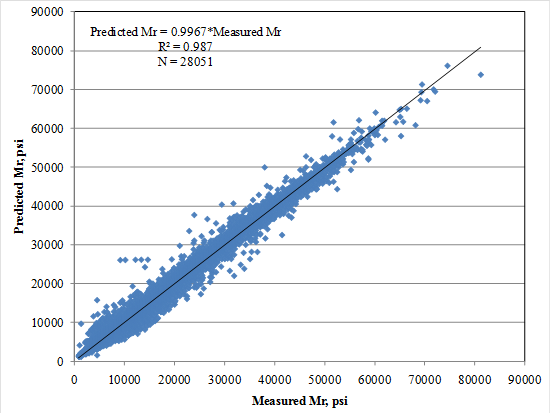
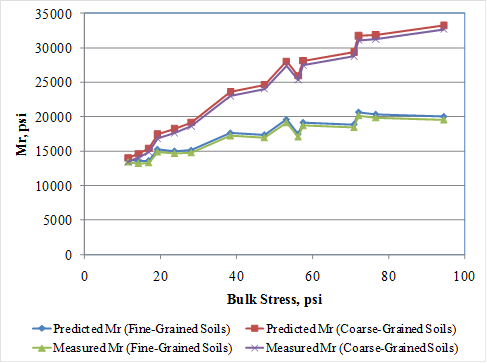
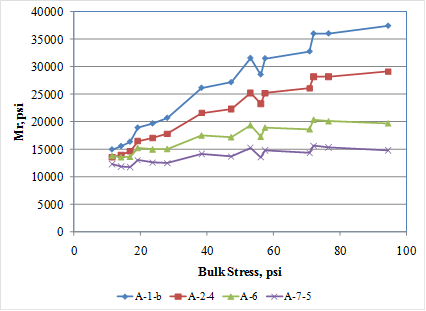
Model prediction accuracy and reasonableness were evaluated by reviewing the plot of predicted and measured resilient modulus for all individual resilient modulus test values used in model development as presented in figure 256. Note that the plot presents actual measured resilient modulus for each individual sample and stress state and resilient modulus computed using predicted k1, k2, and k3 based on actual material properties for each individual sample and the resilient modulus constitutive model and stress state. Figure 257 presents a plot of measured and predicted resilient modulus versus bulk stress for all fine- and coarse-grained materials included in model development database. Note that mean measured k1, k2, and k3 for coarse- and fine-grained materials and predicted k1, k2, and k3 using the equations in figure 70 through figure 72 and mean input values for fine- and coarse-grained materials were used for developing this plot. A review of the plots presented in figure 256 and figure 257 shows a reasonable prediction of resilient modulus.
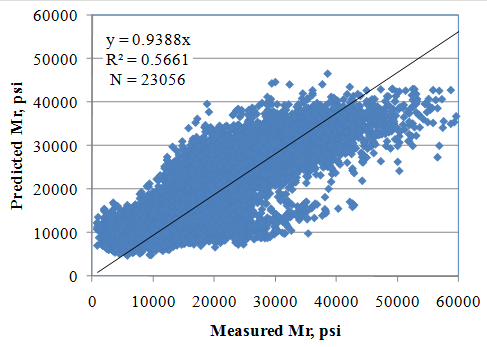
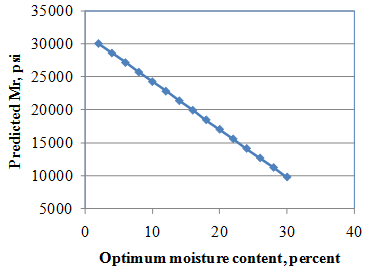
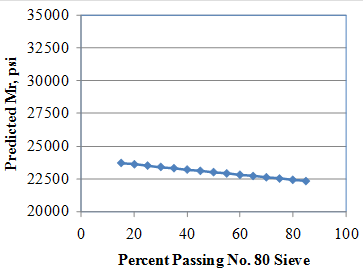
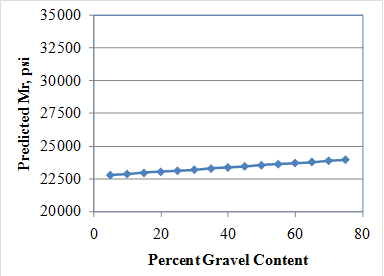
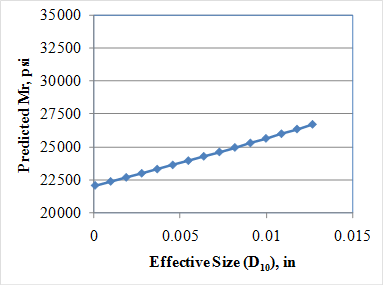
The tentative models were further evaluated by conducting a comprehensive sensitivity analysis. The goal was to determine if the model behaves as expected based on engineering principles. Sensitivity analysis results are presented in figure 258 through figure 264. The results of the sensitivity analysis are summarized as follows:
Overall, the trends observed were deemed reasonable, and the proposed model was established as the recommended model for resilient modulus prediction.
The models developed under this study have been incorporated into a user-friendly software program, Correlations, which can be used independently from the MEPDG. The software, developed under this study, was developed on the Microsoft.NET platform to be compatible with the latest versions of the Microsoft Windows® operating systems. It is programmed in the C# language and uses a modern user interface library to provide a familiar look and feel. It features multiple windows on the user interface that are initially docked inside the main window. These windows can be moved separately from the main window for better viewing of the inputs or results.
The program interface features tabs for PCC, design features, stabilized materials, and unbound materials. Models that belong to each of these categories are made available through a series of radio button selections placed in an accordion control. This placement not only provides the ability to make multiple selections, but it also conserves screen space so that the results of the calculations can be placed for easy viewing. Once a model is selected, the entry area adds controls for the available inputs of the model.
Throughout the software, tooltips are used to provide feedback for each of the areas where data can be entered. Calculations occur after all necessary values have been input. Information about each of the models is available in an information window initially located at the bottom of the screen. This information is context-sensitive to the specific selections that the software user has made. Results of each calculation are displayed prominently in the results area window, initially placed on the right side of the main window.
The software program may be requested from the LTPP Customer Support Service Center at ltppinfo@dot.gov.