Risk analysis is used in the development of a P3 project for a number of reasons:
For major projects in the United States, a series of risk workshops is generally conducted to develop a project risk register, also known as a risk matrix, which is used to manage risks throughout all phases of the project. An example of a risk register is presented in table 3. The risk register will usually comprise the following components:
The risk matrix may also include the results of risk valuation, that is, either a qualitative priority ranking or a quantitative estimate of the potential financial cost or "risk premium" based on the consequence and likelihood of a risk occurrence. This chapter focuses on risk valuation methods.
| Example 1 | |
|---|---|
| Risk category | Right of way (ROW)/Utilities |
| Risk topic | ROW acquisition |
| Impact phase | Construction |
| Risk description | The project is to be constructed in an area that is developing rapidly, so land prices are highly volatile. As a result, the cost of ROW acquisition could be significantly higher than in the current estimate. |
| Consequence of risk | Higher prices in the future would result in an increase in project costs. |
| Ability to transfer risk | It may be possible to transfer this risk in a PPTA contract, but a high-risk premium may be included by offerors if they feel unable to control or influence the underlying economic drivers. It may be more cost-effective for the agency to accept this risk and try to mitigate it. |
Note: PPTA = Public-Private Transportation Act.
Source: From PPTA Risk Analysis Guidance (p. 46), by the Virginia Office of Transportation Public-Private Partnerships, September 2011, Richmond, VA. Copyright
2011 by the Virginia Office of Transportation Public-Private Partnerships. Adapted with permission.
Detailed description of Table 3
Example of a risk register. In P3 (public-private partnerships) projects, a risk register is often prepared in advance to manage risks throughout all phases of the project. In this example, various components of a risk register are presented along with examples of each component. The six typical components of risk register are listed on the table: (1) risk category, (2) risk topic, (3) impact phase, (4) risk description, (5) consequence of risk, and (6) ability to transfer risk. For the risk category, the example provided is right of way (ROW)/Utilities. The example for a risk topic is ROW acquisition. The example listed for the impact phase is construction. For risk description, the project is to be constructed in an area that is developing rapidly, so land prices are highly volatile. As a result, the cost of ROW acquisition could be significantly higher than the current estimate. The consequence of risk is that higher prices in the future would result in an increase in project costs. Finally, in regards to the ability to transfer risk, it may be possible to transfer this risk in a PPTA (Public-Private Transportation Act) contract, but a high-risk premium may be included by offerors if they feel unable to control or influence the underlying economic drivers. It may be more cost-effective for the agency to accept this risk and try to mitigate it.
Qualitative risk analysis includes methods for prioritizing the identified risks for further action. It assesses the priority of identified risks by using their probability of occurrence, the corresponding effect on project objectives if the risks do occur, and the role of other factors, such as the time frame and risk tolerance of the project.
A typical qualitative assessment based on the process used by the Virginia DOT is discussed in this section. Workshop participants are asked to conduct a qualitative risk valuation for each risk by using their professional judgment and experience from previous projects. If available, historic data from similar previous projects and details of specific risk events are used to inform the risk assessment. The valuation is conducted by categorizing risks based on their probability of occurring and cost and schedule impact, as noted in the following paragraphs.
Probability Range - Any risk event that has a probability of occurring of 90 percent or above would be included in the cost estimate and not on the risk register. One of the following options is selected to define the probability of the risk occurring:
Cost Impact - One of the following options is selected to define the cost impact as a percentage of the baseline project cost estimate:
Schedule Impact - One of the following options is selected to define the schedule impact in terms of the period of time that the project would be delayed (or expedited) if a particular risk event were to occur:
Expected risk impact for cost and schedule are automatically categorized based on the rating scales detailed in tables 4 and 5. At this stage of assessment, the impact is classified as very high, high, medium, low, or very low.
The appropriate impact and the color code associated with the risk impact are automatically populated in the risk register once the probability and consequence are selected.
| Probability | Cost Consequence | |||||
|---|---|---|---|---|---|---|
| Greater than 25% | 10%- 25% | 3%-10% | 1%-3% | Less than 1% | ||
| Scale | 5 | 4 | 3 | 2 | 1 | |
| Greater than 70% | 5 | Very High | High | High | Medium | Low |
| 40%-70% | 4 | High | High | Medium | Medium | Low |
| 20%-40% | 3 | High | Medium | Medium | Low | Low |
| 5%-20% | 2 | Medium | Medium | Low | Low | Low |
| 0%-5% | 1 | Low | Low | Low | Low | Very Low |
Note: Yellow = very high to high risk. Light Yellow = medium risk. Green = low to very low risk.
Source: From PPTA Risk Analysis Guidance, by the Virginia Office of Transportation Public-Private Partnerships, September 2011, Richmond, VA. Copyright 2011 by
the Virginia Office of Transportation Public-Private Partnerships. Adapted with permission.
Detailed description of Table 4
Qualitative assessment of cost impact of risk. This table describes the expected risk impact for cost when doing a qualitative risk assessment; at this stage of assessment, the risk impact is classified as Very High, High, Medium, Low, or Very Low. These impacts are color-coded on the table: Very High and High are colored dark yellow; Medium is colored light yellow; Low and Very Low are colored green. On the table there is a column labeled Probability (this stands for the probability range of risk); Probability is classified as Greater than 70 percent; 40 to 70 percent; 20 to 40 percent; 5 to 20 percent; and zero to 5 percent. There is a general column heading labeled Cost Consequence; under this heading are five column sub-headings: Greater than 25 percent; 10 to 25 percent; 3 to 10 percent; 1 to 3 percent; and less than 1 percent. There is a column and a row both labeled Scale; the Scale row classifies Cost Consequence and the Scale column classifies Probability. For both Cost Consequence and Probability, the Scale goes from 1 to 5, 5 being associated with the highest Probability of risk and Cost Consequence and 1 being associated with the lowest Probability of risk and Cost Consequence. For a risk event with a Probability of risk Greater than 70 percent, the Cost Consequence is classified as being Greater than 25 percent; this would be considered a Very High (dark yellow) risk. For the same risk probability category (greater than 70 percent), the cost consequences are as follows: 10 to 25 percent (High risk; dark yellow); 3 to 10 percent (High risk; dark yellow); 1 to 3 percent (Medium risk; light yellow); and less than 1 percent (Low risk; green). For a risk probability of 40 to 70 percent, the cost consequences are as follows: Greater than 25 percent (High risk; dark yellow); 10 to 25 percent (High risk; dark yellow); 3 to 10 percent (Medium risk; light yellow); 1 to 3 percent (Medium risk; light yellow) and less than one percent (Low risk; green). For a risk probability of 20 to 40 percent, the cost consequences are as follows: Greater than 25 percent (High risk; dark yellow); 10 to 25 percent (Medium risk; light yellow); 3 to 10 percent (Medium risk; light yellow); 1 to 3 percent (Low risk; green) and less than one percent (Low risk; green). For a risk probability of 5 to 20 percent, the cost consequences are as follows: Greater than 25 percent (Medium risk; light yellow); 10 to 25 percent (Medium risk; light yellow); 3 to 10 percent (Low risk; green); 1 to 3 percent (Low risk; green) and less than one percent (Low risk; green). Finally, for a risk probability of zero to 5 percent, the cost consequences are as follows: Greater than 25 percent (Low risk; green); 10 to 25 percent (Low risk; green); 3 to 10 percent (Low risk; green); 1 to 3 percent (Low risk; green) and less than one percent (Very low risk; green).
| Probability | Schedule Consequence | |||||
|---|---|---|---|---|---|---|
| Greater than 52 weeks | 16-52 weeks | 4-16 weeks | 1-4 weeks | 0-1 week | ||
| Scale | 5 | 4 | 3 | 2 | 1 | |
| Greater than 70% | 5 | Very High | High | High | Medium | Low |
| 40%-70% | 4 | High | High | Medium | Medium | Low |
| 20%-40% | 3 | High | Medium | Medium | Low | Low |
| 5%-20% | 2 | Medium | Medium | Low | Low | Low |
| 0%-5% | 1 | Low | Low | Low | Low | Very Low |
Note: Yellow = very high to high risk. Light Yellow = medium risk. Green = low to very low risk.
Source: From PPTA Risk Analysis Guidance, by the Virginia Office of Transportation Public-Private Partnerships, September 2011, Richmond, VA. Copyright 2011 by
the Virginia Office of Transportation Public-Private Partnerships. Adapted with permission.
Detailed description of Table 5
Qualitative assessment of schedule impact of risk. This table describes the expected risk when doing a qualitative risk assessment of the impact on a project's schedule in terms of whether the project would be delayed; at this stage of assessment, the schedule impact is classified as Very High, High, Medium, Low, or Very Low. These impacts on this table are color-coded: Very High and High are colored dark yellow; Medium is colored light yellow; Low and Very Low are colored green. On the table there is a column labeled Probability (this stands for the probability range of risk); Probability is classified as Greater than 70 percent; 40 to 70 percent; 20 to 40 percent; 5 to 20 percent; and zero to 5 percent. There is a general column heading labeled Schedule Consequence; under this heading are five column sub-headings: Greater than 52 weeks; 16 to 52 weeks; 4 to 16 weeks; 1 to 4 weeks; and zero to 1 week. There is a column and a row labeled Scale; the Scale row classifies Schedule Consequence and the Scale column classifies Probability. For both Schedule Consequence and Probability, the Scale goes from 1 to 5, 5 being associated with the highest Probability of risk and Schedule Consequence and 1 being associated with the lowest Probability of risk and Schedule Consequence. For a risk event with a Probability of risk Greater than 70 percent, the Schedule Consequence is classified as being Greater than 52 weeks; this would be considered a Very High (dark yellow) risk. For the same risk probability category (greater than 70 percent), the schedule consequences are as follows: 16 to 52 weeks (High risk; dark yellow); 4 to 16 weeks (High risk; dark yellow); 1 to 4 weeks (Medium risk; light yellow); and zero to 1 week (Low risk; green). For a risk probability of 40 to 70 percent, the schedule consequences are as follows: Greater than 52 weeks (High risk; dark yellow); 16 to 52 weeks (High risk; dark yellow); 4 to 16 weeks (Medium risk; light yellow); 1 to 4 weeks (Medium risk; light yellow) and zero to 1 week (Low risk; green). For a risk probability of 20 to 40 percent, the schedule consequences are as follows: Greater than 52 weeks (High risk; dark yellow); 16 to 52 weeks (Medium risk; light yellow); 4 to 16 weeks (Medium risk; light yellow); 1 to 4 weeks (Low risk; green) and zero to 1 week (Low risk; green). For a risk probability of 5 to 20 percent, the schedule consequences are as follows: Â Greater than 52 weeks (Medium risk; light yellow); 16 to 52 weeks (Medium risk; light yellow); 4 to 16 weeks (Low risk; green); 1 to 4 weeks (Low risk; green) and zero to 1 week (Low risk; green). Finally, for a risk probability of zero to 5 percent, the schedule consequences are as follows: Greater than 52 weeks (Low risk; green); 16 to 52 weeks (Low risk, green); 4 to 16 weeks (Low risk; green); 1 to weeks (Low risk; green) and zero to 1 week (Very low risk; green).
Quantitative risk analysis is performed on risks that have been prioritized by the qualitative risk analysis process as potentially and substantially impacting the project. Quantitative risk analysis is conducted to quantify risks in terms of both cost and time impact. Two alternative levels of quantitative risk analysis may be undertaken:
A risk workshop is an effective tool for gaining expert insight into the quantification of risk probability and potential impact. Quantitative risk analysis allows an agency to conduct a VfM assessment during the preprocurement phase, as well as after bids are received. A quantitative risk analysis may also be helpful in developing key contract terms. The approaches used by Virginia DOT for quantitative analysis are discussed in the following sections.
With this risk assessment approach used by Virginia DOT, workshop attendees determine specific values for:
The following formula is then used to calculate the risk value of each individual risk:
Risk Value = Probability of Occurrence × (Min + Max + 4 × ML)â„6
The formula presumably attempts to replicate very simply the result that might be obtained with a more sophisticated analysis that uses simulation (discussed in the next section). A contingency amount may be added to account for unknown risks.
Many risk events are likely to have an impact on both cost and schedule. Schedule impact is quantified in units of time, but delays also have a cost associated with them. The direct cost impacts of risk events are accounted for under the analysis of cost risk, but indirect costs from delays are not. Indirect costs from delays include the added interest costs of financing and the cost of running site offices, utilities, and the time cost of engineers, inspectors, and administration staff. Indirect costs include agency indirect costs (including independent oversight/construction management) and the contractor's indirect costs. The total cost of delay is the sum of the agency indirect costs and the contractor's indirect costs. In addition, in the case of a tolled facility, there will be a loss of revenue that will also need to be accounted for.
To get a complete picture of total potential project cost, the agency can calculate the dollar value of schedule impacts by calculating a "per week" value for indirect costs and by multiplying this unit rate by the expected schedule impact/delay associated with the risk event. An average rate may be used for risk events during construction, and a second value may be used for risk events during operations. Historic data may be used to verify the amounts.
Sensitivity analysis may be used to evaluate financial outcomes when critical assumptions are changed. This can help decisionmakers to better understand how assumptions shape the expected outcomes of a project and to anticipate the types of conditions that might trigger remedial actions. Sensitivities on key financial and operating conditions may be undertaken through a number of likely scenarios, such as low-, middle-, and high-risk cases. This will provide a more accurate reflection of the potential spread of the total cost to the public agency.
A Monte Carlo simulation (named after the Monte Carlo casino where the uncle of one of the creators of the technique gambled away his money) produces a deterministic sample set of likely project outcomes and the probabilities of their occurrence. The sample set is then used to develop distributions and ranges for aggregate cost and schedule impacts. The simulation provides a range of aggregate risk values that the agency may choose from, depending on what confidence threshold is required. This is not possible with a formula-based analysis.
Monte Carlo methods, however, require knowledge and training for their successful implementation. Input to Monte Carlo methods also requires the user to know and to specify exact probability distribution information, including mean, standard deviation, and distribution shape. The process is as follows:
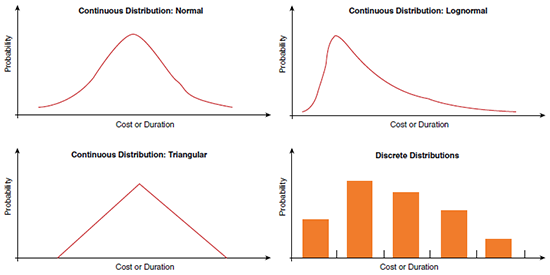
Figure 2. Distributions for risk analysis. From Guidebook on Risk Analysis Tools and Management Practices to Control Transportation Project Costs (NCHRP Report 658), by Molenaar, A., Anderson, S., & Schexnayder, C., 2010, Washington, DC: Transportation Research Board. Copyright 2010 by the Transportation Research Board. Adapted with permission.
Detailed description of Figure 2
Distributions for risk analysis. This figure is made up of four graphs (three line graphs and one bar graph); each graph is an example of assumption curves of a Monte Carlo simulation. On each graph the x-axis is labeled Cost or Duration and the y-axis is labeled Probability. The first graph is labeled Continuous Distribution: Normal; on this graph Cost or Duration goes up as Probability increases and then goes down again, forming an evenly spaced parabola. The second graph is labeled Continuous Distribution: Lognormal; on this graph Cost or Duration goes up sharply as Probability increases and then goes down sharply. The third graph is labeled Continuous Distribution: Triangular; on this graph cost or duration rises steadily as probability increases, then drops just as steadily as probability decreases, forming a right triangle. Finally, the fourth graph is labeled Discrete Distributions. This is a bar graph showing five orange-colored bars. The first bar from the left is relatively short and the second bar is the tallest; the third through fifth bars then get gradually shorter (representing a decrease in cost or duration) as probability goes down.
Examples of assumption curves are shown in figure 2. The curves are probability distributions with different mean values and different standard deviation values. All four distributions have a single high point (the mode), and all have a mean value that may or may not equal the mode. Some of the distributions are symmetrical about the mean, whereas others are not. Selecting an appropriate probability distribution is a matter of which distribution is most like the distribution of actual data. For transportation projects, this is a difficult choice, because historical data on unit prices, activity durations, and quantity variations are often difficult to obtain. In cases in which data are insufficient to completely define a probability distribution, one must rely on a subjective assessment of the needed input variables.
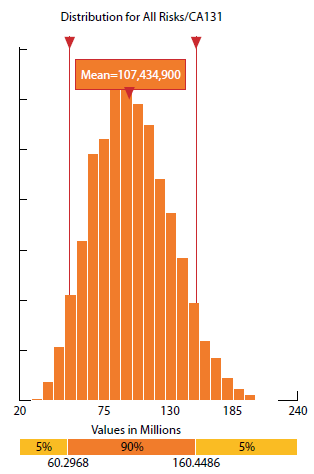
Figure 3. Risk distribution histogram. CA131 = California State Highway 131. From PPTA Risk Analysis Guidance (p. 23, figure 6) by the Virginia Office of Transportation Public-Private Partnerships, September 2011, Richmond, VA. Copyright 2011 by the Virginia Office of Transportation Public-Private Partnerships. Adapted with permission.
Detailed description of Figure 3
Risk distribution histogram. This bar graph depicts is an example of one of the types of impact distribution graphs that may be generated by Monte Carlo simulation software; this particular graph uses data from a simulation done on California State Highway 131 (CA 131). The y-axis shows increasing risk. The x-axis measures Values in Millions (dollars) from 20 to 240 in increments of 55 (20, 75, 130, 185, 240). Â The x-axis also shows the lowest 5 percent of risk in millions of dollars (approximately 57 million), the middle 90 percent (between 57 and 67 million, approximately), and the highest five percent (approximately 67 to 200 million). The mean value is $107,434,900.
The main output of the simulation is total values for retained, transferred, and shared risks. Several types of charts may be generated automatically by the Monte Carlo simulation software. Examples of impact distribution graphs are presented in figures 3 and 4. Aggregated risks through the use of a histogram are displayed in figure 3, and an alternative method of displaying cumulative risks with an S-curve is shown in figure 4.
The S-curve allows values to be used based on the confidence level required for the project. In figure 4, the 50th percentile (also known as the P50), mean, and 80th percentile (P80) are shown because these are the most commonly reported statistics. The mean represents the average of all generated outputs, which is not the same as the P50 unless the distribution is symmetrical. The confidence level selected will depend on the stage of assessment, confidence in cost estimates, and complexity of the project. The P80 is widely used by public agencies in risk analysis at earlier stages, when project information is less well-developed, to show a confidence level of 80 percent that risk costs will not exceed the estimated value. It should be noted that the public and private sectors have different preferences with regard to the confidence level. For example, a risk-averse public agency may use P90 as its confidence level preference, whereas private entities may be more comfortable using a P50 confidence level.
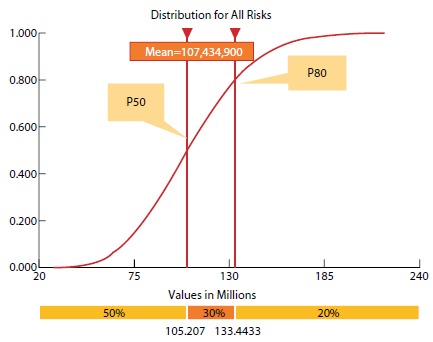
Figure 4. Risk distribution S-curve showing confidence levels. P50 = 50th percentile, P80 = 80th percentile. From PPTA Risk Analysis Guidance (p. 23, figure 7), by the Virginia Office of Transportation Public-Private Partnerships, September 2011, Richmond, VA. Copyright 2011 by the Virginia Office of Transportation Public-Private Partnerships. Adapted with permission.
Detailed description of Figure 4
Risk distribution S-curve showing confidence levels. This S-curve depicts is an example of one of the types of impact distribution graphs that may be generated by Monte Carlo simulation software. The y-axis depicts increasing levels of risk (zero to 1.000 in increments of .200). The x-axis shows Values in Millions (dollars); it also shows the 50th percentile (P50, or $105,207,000), the mean ($107,434,900), and the 80th percentile (P80, or $133,443,300). The S-curve starts out low and flat; gradually rising past the 50th percentile, the mean, and the 80th percentile; plateauing around $157,000,000 (approximately 1.000 risk).
