U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-049 Date: August 2014 |
Publication Number: FHWA-HRT-14-049 Date: August 2014 |
The governing equation for the free transverse vibration of a taut string is as follows:(4)
![]()
Figure 1 . Equation. Equation of motion (EOM) for a taut string.
Where:
H = Axial tension force in a string or cable.
y = Transverse in-plane displacement due to vibration.
ρ = Mass density per unit volume.
A = Cross-sectional area of the string, beam, or cable.
t = Time.
x = Distance.
The equation in figure 1 may be rewritten as follows:
![]()
Figure 2 . Equation. One-dimensional wave propagation.
Where c is the phase velocity, which is defined as follows:
![]()
Figure 3 . Equation. Phase velocity.
Applying the method of separation of variables, a general solution to the equation from figure 1 with a fixed-fixed end condition may readily be derived as follows:
![]()
Figure 4 . Equation. General solution of EOM of a taut string.
Where:
ωn = Natural angular frequency of the nth mode of vibration.
kn = Wave number of the nth mode of vibration.
Cn = Amplitude of in-plane displacement due to vibration.
αn = Phase angle of time-dependent part of transverse in-plane displacement due to vibration.
n = Mode number.
The angular frequencies and wave numbers are not independent of each other but are interrelated as follows:
![]()
Figure 5 . Equation. Relationship between angular frequency and wave number.
Where:
L = Length of the string.
The equation in figure 4 indicates that the motion of the string is represented by a superposition of standing waves with mode shapes of sin knx and time-varying amplitudes of Cncos(ωnt - αn).
The natural frequencies, ωn, are the eigenvalues representing the discrete frequencies at which the system is capable of undergoing harmonic motion.
The equation in figure 1 is a linearized EOM in which nonlinearities arising from finite sag are ignored. Note that the only significant parameters in figure 1 through figure 5 are L, H, and ρA. Also note that from the equation in figure 5, ωn is proportional to the mode number, n.
From the equations in figure 3 and figure 5, the cable tension H can be determined from the fundamental natural frequency, f, as follows:
![]()
Figure 6 . Equation. Cable tension.
f, in Hz is related to the angular frequency ω such that f = ω/2π.
The governing equation for the free transverse vibration of a Bernoulli-Euler beam is given by the following:(4)
![]()
Figure 7 . Equation. EOM for a classical beam.
Where:
E = Young's modulus.
I = Moment of inertia.
The equation in figure 7 may be rewritten as follows:
![]()
Figure 8 . Equation. EOM for a classical beam, rewritten with vibration parameter.
Where a is defined as the vibration parameter for classical beam, which can be solved as follows:
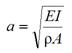
Figure 9. Equation. Vibration parameter for a classical beam.
Note that the equation in figure 8 is not of the wave equation form and that a does not have the dimension of velocity. Applying the method of separation of variables, a general solution to the equation in figure 8 with a pinned-pinned end condition can be derived and takes the form of the equation in figure 4, with ωn and kn being interrelated as follows:
![]()
Figure 10 . Equation. Relationship between angular frequency and wave number.
The significant parameters in this formulation are L, EI, and ρA. Note that ωn ∝ n2.
VIBRATION OF TAUT STRINGS WITH FLEXURAL STIFFNESS
The governing equation for the free transverse vibration of a taut string with flexural rigidity or, equivalently, a classical beam with axial tension, is given by the following equation:
![]()
Figure 11 . Equation. EOM for a taut string with flexural stiffness.
A general solution to the equation in figure 11 with a pinned-pinned end condition can be derived and again takes the form of the equation in figure 4, with ωn and kn being interrelated as follows:
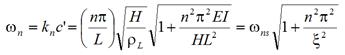
Figure 12 . Equation. Relationship between angular frequency and wave number for a string.
Or equivalently as follows:
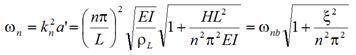
Figure 13 . Equation. Relationship between angular frequency and wave number for a beam.
Where:
ρL = Cable mass per unit length.
ξ = Flexural stiffness parameter.
ωnb = Natural angular frequency of a classical beam in the nth mode of vibration.
ωns = Natural angular frequency of the taut string in the nth mode of vibration.
The parameter ξ in figure 12 and figure 13 is defined as follows:(5)
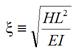
Figure 14 . Equation. Flexural stiffness parameter.
For the equation in figure 11, the first term, accounting for the effect of flexural stiffness, is added to the taut-string equation presented in figure 1. The equation in figure 12 indicates that the natural vibration frequencies of a taut string with flexural rigidity can be expressed in terms of those of the simple taut string when appropriate factors are multiplied. The same case may be viewed as a beam with axial tension, and the natural frequencies can be expressed in terms of those of the beam with appropriate factors multiplied as shown in figure 13. The flexural stiffness parameter defined by the equation in figure 14 represents the relative influence of the axial tension over the flexural stiffness in cable vibration.
The solutions presented in figure 12 and figure 13 are for cables with pinned-pinned end conditions. Analysis of cables with fixed-fixed end conditions is more complex and requires the solution of transcendental equations.
VIBRATION OF TAUT STRINGS WITH FLEXURAL STIFFNESS AND SAG-EXTENSIBILITY
The governing equation for the free transverse vibration of a taut string with transverse flexural rigidity and sag-extensibility is as follows:(6,7)
![]()
Figure 15 . Equation. EOM for a taut string with flexural stiffness and sag-extensibility.
Where:
h = Horizontal component of tension force due to vibration.
ys = Transverse in-plane displacement due to weight.
No closed-form solution to the equation in figure 15 is available; however, approximate solutions for certain boundary conditions are available. The vibration frequencies of a cable with fixed-fixed end condition can be expressed in terms of those of the taut string as follows:
![]()
Figure 16 . Equation. Approximate solution to the EOM for a taut string with flexural stiffness and sag-extensibility.
Where:
α = Correction factor for sag-extensibility effects, which is defined in figure 17.
βn = Bending stiffness correction factor for nth mode of vibration.
μ = Mass parameter.
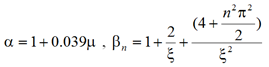
Figure 17 . Equation. Correction factor for sag-extensibility and bending stiffness.
The sag-extensibility parameter, λ2, is defined as follows:
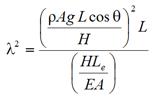
Figure 18. Equation. Sag-extensibility parameter.
Where:
θ = Inclination angle of the cable.
g = Gravitational constant.
Le = Effective length of the cable, which is defined as follows:
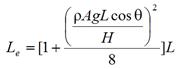
Figure 19. Equation. Effective length of cable.
The additional tension h due to cable vibration adds nonlinearity to the formulation and is determined by the equation in figure 20.

Figure 20 . Equation. Additional tension force due to cable vibration.
The parameter α in figure 16 is given by the following:
![]()
Figure 21. Equation. Correction factor for sag-extensibility.
The parameter μ in figure 16 is given by the following:
![]()
Figure 22. Equation. Mass parameter.
The two parameters λ2 and ξ a major role in the formulation in figure 14 and figure 15. The relationship of the equation in figure 16 is known to provide a good approximation when λ2 < 3 and ξ > 50, and many stay cables in cable-stayed bridges fall within this range.