U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-049 Date: August 2014 |
Publication Number: FHWA-HRT-14-049 Date: August 2014 |
This chapter illustrates some common issues on finite element analysis of stay cables using examples. First, single cables with varying degrees of complexity were treated. Then, systems with two stay cables interconnected with a transverse crosstie were analyzed. Finally, a stay cable system in an actual cable-stayed bridge that was previously analyzed by other investigators using a non-FEM was analyzed using FEM, and the results were compared.
For analysis, finite element analysis software SAP2000® was used.(8) Beam elements with appropriate properties were used to model the stay cables and crossties, and the P-delta analysis technique was used to account for the effects of pre-tensioned forces in the stay cables and crossties.
NUMERICAL MODELING AND ANALYSIS OF STAY CABLES
In the first example, the transverse vibration of a stay cable, modeled as a taut string with fixed ends, was analyzed using FEM and compared with the theoretical solution. The cable had the following fictitious properties:
A beam element with zero flexural stiffness and subjected to axial tension was used to model a taut string. (In practice, a negligibly small number is used for flexural stiffness to avoid numerical instability.)
An illustration of the cable along with the input data and sample results is presented in figure 23. The results from finite element analysis are shown to match theoretical solutions. T1 and T2 denote the period of the first and second mode, respectively. The first 4 vibration mode shapes calculated are shown in figure 24, and the natural vibration frequencies for the first 10 modes are shown in figure 25. The natural frequency is a linear function of the mode number.

Figure 23 . Illustration. Analysis of a simple taut string.
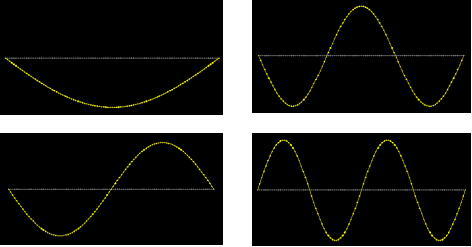
Figure 24 . Image. The first four mode shapes for the vibration of a taut string.
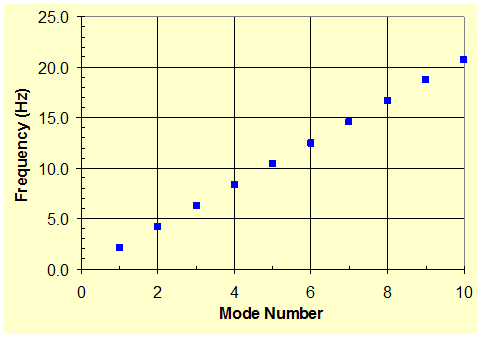
Figure 25 . Graph. Natural vibration frequencies of a taut string.
The vibration of an Euler-Bernoulli (or classical) beam with hinge-hinge end conditions was analyzed using FEM and compared with theoretical solutions. The beam has the same length and density as the string model discussed previously. The beam is assumed to have a circular cross section with a diameter of 1 inch (25.4 mm) and is made of steel with a Young's modulus of 2.9E+7 psi (200 GPa).
An illustrative problem with sample input and output data is presented in figure 26. The results from the numerical analysis match the theory. The first 10 natural frequencies are presented in figure 27. The natural frequency of a classical beam is a quadratic function of the mode number, as predicted by the equation in figure 10.

Figure 26 . Illustration. Analysis of a classical beam.
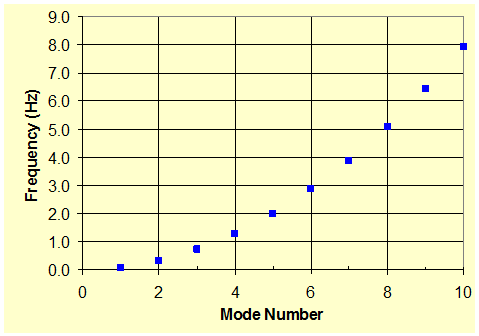
Figure 27 . Graph. Natural vibration frequencies of a classical beam.
Taut String with Flexural Stiffness
The vibration of a taut string with finite flexural stiffness (or a beam-column) was analyzed. A flexural stiffness parameter (ξ) of 82.4 was computed according to the equation in figure 14, and hinge-hinge end conditions were used. The problem is described schematically in figure 28. Results from numerical analysis match the analytical solutions discussed in the section, "Vibration of Taut Strings with Flexural Stiffness" in chapter 2.

Figure 28 . Illustration. Analysis of a taut string with finite flexural stiffness and pinned-pinned ends.
The natural frequencies of the taut string with flexural stiffness and those of the taut string without flexural stiffness are shown in figure 29. It can be seen that taking into account the flexural stiffness generally increases the natural frequencies of its transverse vibration. The significance of flexural stiffness, however, is very limited for lower-order vibration modes but picks up noticeably with increasing mode number.
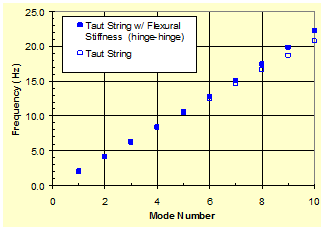
Figure 29 . Graph. Natural vibration frequencies of a taut string with finite flexural stiffness and hinge-hinge supports.
A similar problem with fixed-end conditions was also analyzed. The finite element solutions match those predicted by an approximate formula by Mehrabi and Tabatabai, as seen in figure 30.(6) No closed form solution is known to exist for this problem.

Figure 30 . Illustration. Analysis of a taut string with finite flexural stiffness and fixed-fixed ends.
In figure 31, the influence of cable end conditions, whether fixed or hinged, on natural frequencies is compared. Relatively small differences are observed between the two cases. However, the differences increase with increasing mode number.
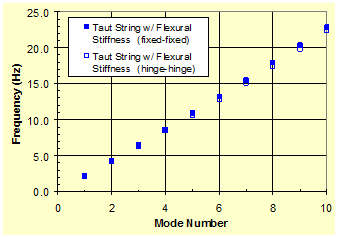
Figure 31 . Graph. Natural vibration frequencies of a taut string with finite flexural stiffness and two different support conditions.
TWO-CABLE SYSTEM WITH CROSSTIE
A simple system of two twin cables interconnected by a cross tie was analyzed (see figure 32). An optional tie to the ground was also considered. Each cable has the same dimensions and properties as the single cable introduced in the previous example (L = 1,000 inches (25.4 m), H = 10 kip (44.5 kN), ρL = 0.222 lbm/inch (3.96 kg/m), D = 1 inch (25.4 mm), fixed-fixed ends). The ties are modeled as an elastic spring, and a number of combinations of stiffness values (K and KG) are considered, where K is the stiffness between two cables, and KG is the stiffness between the cable and the ground or bridge deck.
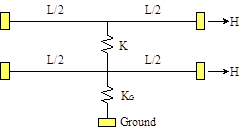
Figure 32 . Illustration. Two-cable system with crossties.
First, the in-plane free vibration of this system was analyzed. Figure 33 shows the evolution of the natural frequency of a system when K = 0 and KG = 0 (i.e., when there are no crosstie or anchorage connecting the two cables). Figure 34 shows results when K is finite (K = 0.1 kip/inch (7.5 kN/m)) and KG = 0. It can be seen from figure 34 that the frequencies for n = 2, 6, 10, ... are increased by the presence of a crosstie (spring) between the cables. Figure 35 shows the evolution of mode-frequencies when both K and KG have finite spring constants.
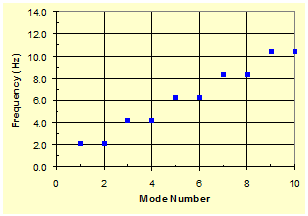
Figure 33 . Graph. Mode-frequency evolution for a two-cable system with K = 0 and KG = 0.
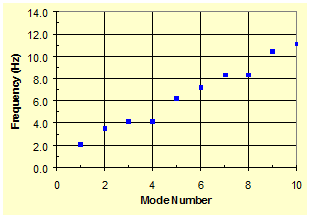
Figure 34 . Graph. Mode-frequency evolution for a two-cable system with K = finite and KG = 0.
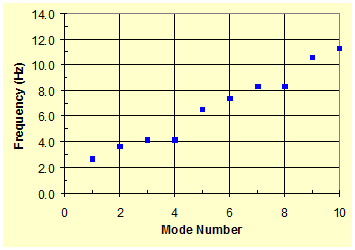
Figure 35 . Graph. Mode-frequency evolution for a two-cable system with K = finite and KG = finite.
From figure 35, it is apparent that anchoring the crosstie to the ground increases the frequencies (for n = 1, 2, 5, 6, ...) of the two-cable system. Figure 36 shows the evolution of natural frequency of a system when both springs are rigid (K → infinite, KG → infinite). Due to the rigid support of the cables at their midpoints, the first two vibration modes of the unrestrained free cables were suppressed, and thus the first four consecutive modes have the same frequencies, etc.
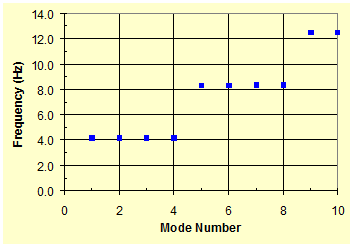
Figure 36 . Graph. Mode-frequency evolution for a two-cable system with K → infinite and KG → infinite.
Two selected mode shapes from the finite element analysis in comparison with those presented by Caracoglia and Jones are shown in figure 37.(9) The crosstie deforms only for modes n = 2, 6, 10, etc. For all other modes, the crosstie moves as a rigid body. The same parameters (K = 0.1 kip/inch (7.5 kN/m) and KG = 0) as in the case of figure 34 were used. An analytically based and numerically implemented method, which does not involve any finite element procedure, was developed by Caracoglia and Jones and used for the analysis of the in-plane free-vibration of a set of interconnected taut cable elements.(9) The results from the two different approaches are the same.
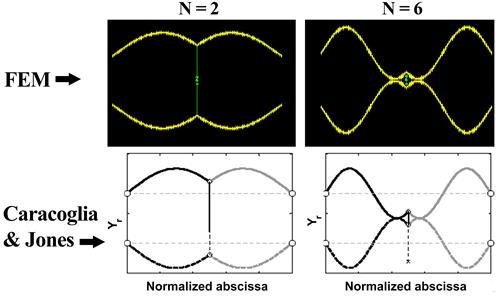
Reprinted with permission from Elsevier
Figure 37 . Image. Comparison of mode shapes from finite element analysis (top) and from Caracoglia and Jones (bottom).(9)
The mode-frequency evolution of a two-cable system with various combinations of crosstie stiffnesses was analyzed and is presented in figure 38. The top enveloping curve corresponds to the case with a rigid crosstie and a rigid ground tie. The bottom enveloping curve corresponds to the case with no crosstie and no ground tie. The two other cases fall in between these two extreme cases, and the corresponding mode-frequency evolution curves stay within the top and bottom enveloping curves of these two extreme cases. The curves clearly show the stiffening effect of the crosstie and anchorage, resulting in increased natural frequencies of the system.
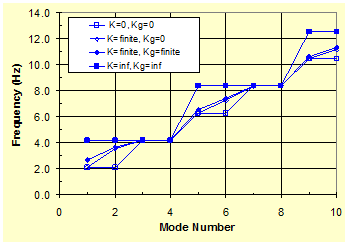
Figure 38 . Graph. Mode-frequency evolution for a two-cable system with various combinations of crosstie stiffnesses.
Analysis was extended to a real full-scale cable network. The Fred Hartman Bridge in Houston, TX, was selected for illustration and comparison purposes. Photos of the bridge and cable network are presented in figure 39 and figure 40, respectively. The results from finite element analysis are compared with those from the analytical method by Caracoglia and Jones wherever possible.(10)

Figure 39 . Photo. Fred Hartman Bridge in Houston, TX.

Figure 40 . Photo. The cable network of the Fred Hartman Bridge in Houston, TX.
Finite element discretization of a network of main-span stay cables (A-line) of the Fred Hartman Bridge is shown in figure 41. The stay cables are interconnected with three lines of crossties. The configuration shown represents an equivalent two-dimensional (2D) network reduced by Caracoglia and Jones from the original three-dimensional (3D) network.(10) The analytical method developed by Caracoglia and Jones is designed for 2D networks, whereas finite element analysis simulates up to 3D configurations. For comparison purposes, however, the 2D equivalent network generated by Caracoglia and Jones is used here. Analysis is confined to the in-plane free vibration of the network.
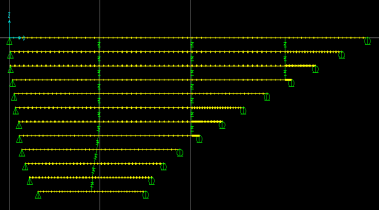
Figure 41 . Image. Finite element model for the stay cable system of the Fred Hartman Bridge in Houston, TX.
The first four in-plane vibration mode shapes of the cable network from the finite element analysis and from Caracoglia and Jones are shown in figure 42. The mode shapes from these two different calculations are the same. Some minute discrepancies are attributed to intrinsic differences in the analysis procedure of the two approaches. The modes shown in figure 42 are global in nature in that the majority of the cable segments participate in the oscillation. For n = 1 and 2, modes are clearly global. However, for n = 3 and 4, some local behaviors are superimposed on global behaviors.
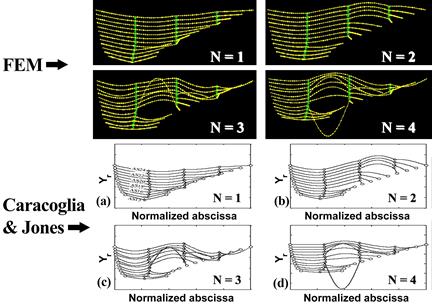
Reprinted with permission from Elsevier
Figure 42 . Image. First four vibration mode shapes of the Fred Hartman Bridge stay cable system from finite element analysis (top) and from Caracoglia and Jones (bottom).(10)
As the mode number increases, local modes, in which the response of the network is limited to some intermediate segments of cables, become evident. Figure 43 shows mode shapes for n = 5–8. The wavelengths in these vibration modes are dictated by the distances between two adjacent crossties. Subsequent vibration modes, densely populated in frequency, are seen to be a permutation of a similar pattern dominated by a few cables. Local modes are found to dominate for up to n = 28.
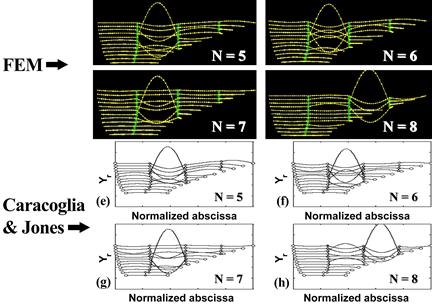
Reprinted with permission from Elsevier
Figure 43 . Image. Vibration mode shapes 5–8 of the Fred Hartman Bridge stay cable system from finite element analysis (top) and from Caracoglia and Jones (bottom).(10)
However, a second set of global network modes occurred at n = 29 and continued for a few modes and then local modes resumed. This global-local pattern repeats thereafter. Figure 44 shows mode shapes for n = 29–32. Global modes of vibration are noticeable for n = 29–31, and thereafter, local modes resumed.
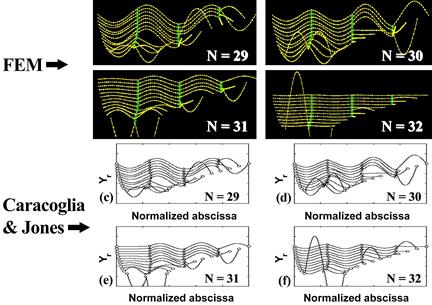
Reprinted with permission from Elsevier
Figure 44 . Image. Vibration mode shapes 29–32 of the Fred Hartman Bridge stay cable system from finite element analysis (top) and from Caracoglia and Jones (bottom).(10)
The modal characteristics of the network are illustrated in figure 45 in the mode-frequency evolution chart where the natural frequency of the network is plotted as a function of the mode number.
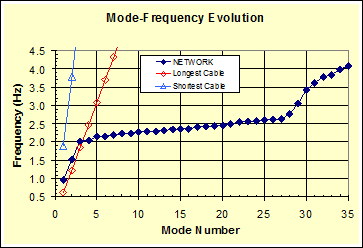
Figure 45 . Graph. Mode-frequency evolution for the Fred Hartman Bridge stay cable system from finite element analysis.
The figure shows that a sequence of global modes are followed by a plateau of densely populated local modes, which is then followed by a second set of global modes, etc. This pattern of consecutive steps is typical of the modal behavior of a cable network. Figure 45 shows that the fundamental frequency (n = 1) of the network is bracketed between the fundamental frequencies of the longest and shortest cables. The presence of crossties is seen to enhance the overall performance of the network by increasing their natural frequencies, especially those of global modes. However, analysis also suggests that the presence of crossties may not necessarily be beneficial at plateau frequencies due to potentially undesirable effects associated with densely populated local modes.
The mode-frequency evolution chart generated by Caracoglia and Jones is presented in figure 46 for comparison.(10) The finite element results presented in figure 45 correspond to their analysis case, "NET_3C." Overall, the results from both approaches are the same.
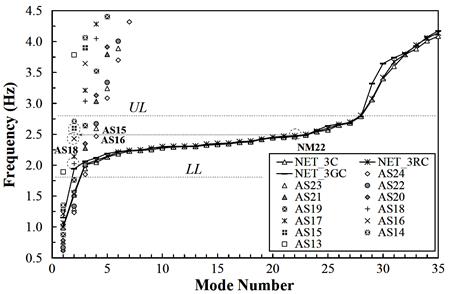
Reprinted with permission from Elsevier
Figure 46 . Graph. Mode-frequency evolution for the Fred Hartman Bridge stay cable system.(10)
Variations in Crosstie Configuration
As a modification to the original configuration, two shorter crossties were tied to the ground (i.e., the deck), as shown in figure 47. The resulting mode shapes (for n = 1 and 2) are presented in figure 48. The first mode is quite similar to that of the previous (reference) network. However, the second mode is rather different from the case of the reference network due to anchoring of the middle line of crosstie.
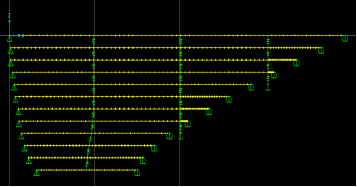
Figure 47 . Image. Finite element model for the stay cable system with some crossties anchored to the deck.
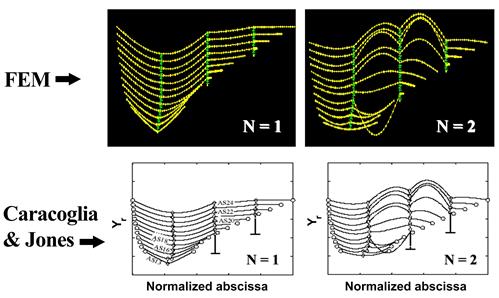
Reprinted with permission from Elsevier
Figure 48 . Image. First two vibration mode shapes for the model shown in figure 47 from finite element analysis (top) and from Caracoglia and Jones (bottom).(10)
The effect of crosstie anchoring was examined in terms of the mode-frequency evolution behavior, which is shown in figure 49. The addition of grounding ties significantly increased the frequencies of global modes but did not increase the frequencies of local modes by a significant amount. Grounding of crossties apparently made the network stiffer with respect to its global behavior, but it practically did not affect the local vibration responses of individual cables.
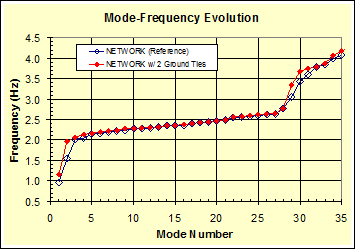
Figure 49 . Graph. Comparison of mode-frequency evolution for models shown in figure 41 (reference) and figure 47.
As another fictitious variation to the original configuration, the geometry of the two shorter restrainers was modified, as shown in figure 50. This modification helps avoid excessive stretch of the segments of some cables due to the grounding of crossties. This modification would avoid undesirable stress concentrations in these cable segments.
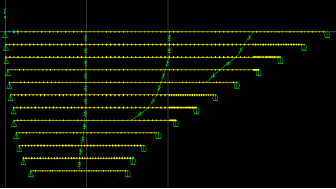
Figure 50 . Image. Finite element model for the stay cable system with a varied crosstie configuration (variation 1).
The first four vibration mode shapes for this variation are shown in figure 51, and the mode-frequency evolution is shown in figure 52. This variation renders slightly lower frequencies of global modes and yet somewhat higher frequencies of local modes. The step behavior of the original configuration is slightly rounded. Comparing figure 51 with figure 42 suggests an improvement of this variation over the original configuration by avoiding the presence of very short segments of cables.
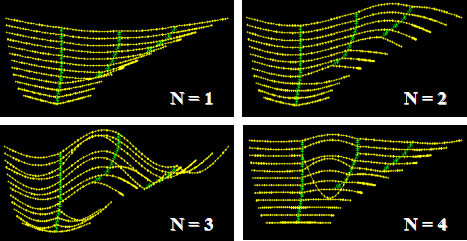
Figure 51 . Image. Vibration mode shapes 1–4 for the model shown in figure 50.
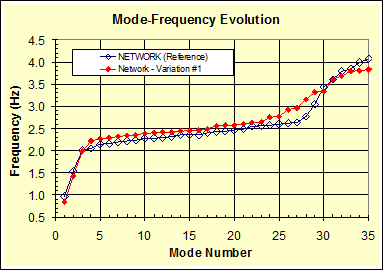
Figure 52 . Graph. Comparison of mode-frequency evolution for models shown in figure 41 (reference) and figure 50.
The third variation to the original crosstie configuration involves only a single line of crossties as shown in figure 53. Figure 54 shows the first four mode shapes of this variation, and figure 55 shows the corresponding mode-frequency evolution (in solid diamonds) in contrast to that of the reference configuration. Clearly, it can be seen that the single line of crossties provides less reinforcement to the cable system. More frequent global-local steps occur as the quantity of crossties is reduced.
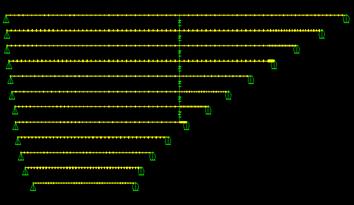
Figure 53 . Image. Finite element model for the stay cable system with a single crosstie line (variation 2).
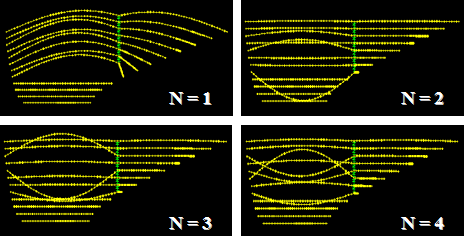
Figure 54 . Image. Vibration mode shapes 1–4 for the model shown in figure 53.
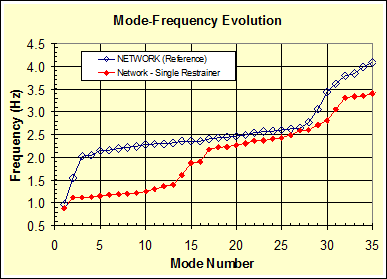
Figure 55 . Graph. Comparison of mode-frequency evolution for models shown in figure 41 (reference) and figure 53.
Finally, the mode-frequency evolution behavior of the original network over extended mode numbers (up to n = 100) is shown in figure 56. Multiple repeated global-local behaviors can be seen.
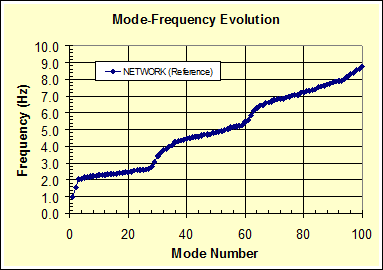
Figure 56 . Graph. Mode-frequency evolution for higher mode numbers.