U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-049 Date: August 2014 |
Publication Number: FHWA-HRT-14-049 Date: August 2014 |
In chapter 4, free-vibration analysis of stay cable systems networked with diverse configurations of crossties was discussed, and the mode-frequency evolution of each case was investigated. Although the mode-frequency information sheds light on some important dynamic properties of a cable system, the actual performance of the system under different wind events is difficult to assess solely based on such information. A time-history analysis under realistic wind loading allows more explicit and detailed information to be obtained about the system's dynamic structural performance.
To date, the effectiveness of crossties in mitigation of stay cable vibrations was solely assessed indirectly in terms of the modal properties of the system. Increases in natural frequencies of a cable system have been interpreted as enhancement in mitigation, which is based on the idea that the threshold wind speeds triggering certain aerodynamic instabilities (e.g., vortex shedding) are proportional to the fundamental natural frequency of the system. However, the performance of a cable system under a variety of wind events cannot be deduced from changes in modal properties of the system. An explicit time-history analysis of a cable system subjected to time-varying wind forces should be conducted to understand the performance of the system and assess the effectiveness of a mitigation measure implemented.
A set of wind profiles was selected and used in the time-history analysis. These profiles are based on anemometer data retrieved at the Bill Emerson Memorial Bridge in Cape Girardeau, MO. Some profiles were artificially transformed in order to simulate certain wind conditions.
Figure 97 shows the reference wind speed profile, which will be referred to as "wind-1" throughout the current study. The profile represents a 5-min wind speed record measured at the Cape Girardeau bridge site, except that the profile is scaled up such that the peak 3-s gust speed reaches 98 ft/s (30 m/s). In order to prevent an erroneous oscillation due to suddenly applied loading at the beginning (t = 0 s) of the analysis, an artificial ramp of wind loading was added between t = 0 and 10 s. The initial velocity of the wind was fully recovered at t = 10 s.
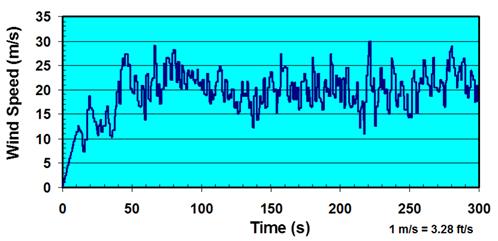
Figure 97 . Graph. Reference wind speed profile.
The frequency-amplitude spectrum for this reference profile is shown in figure 98. The profile contains large amplitude low-frequency components with a significant static value, which is related to a large nonzero mean speed in the time profile. The amplitude gradually decreases with increasing frequency, especially for f > 1 Hz.
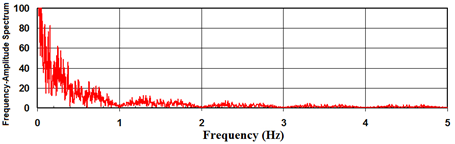
Figure 98 . Graph. Frequency-amplitude spectrum for the wind speed profile shown in figure 97.
Figure 99 shows the wind force profile computed from the wind speed profile shown in figure 97. For simplicity, only wind-induced drag force was taken into account in converting the wind speed into the wind force. There are a number of mechanisms and conditions that contribute to wind pressures on stay cables. It is not always feasible to predict wind pressure on stay cables from a given wind speed profile without detailed knowledge of the structural and aerodynamic conditions of the cables and wind involved. As a first step, a simplified situation in which the drag force is a dominant wind-induced pressure on the stay cables was considered. Pressures from other sources, when justified to be present and quantifiable, may be added. The wind force (per unit length) profile was applied in the direction of the bridge longitudinal axis, inducing in-plane vibration of the cable network (see figure 99).
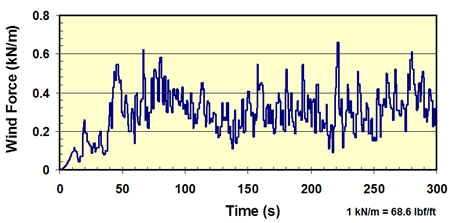
Figure 99 . Graph. Wind force based on wind speed profile shown in figure 97.
To simulate the moving wind, a sequential loading scheme was used (see figure 100). The cable network was divided into five zones, and each zone was sequentially exposed to the moving wind with a time interval, T. For example, zone II was exposed to the same wind force profile that zone I was exposed to T-second ago. The time interval is estimated by dividing the horizontal transverse distance (x) by the average horizontal wind speed (Vavg) of the wind profile. For example, T = 1.4 s for x = 90.97 ft (27.734 m) and Vavg = 65.6 ft/s (20 m/s).
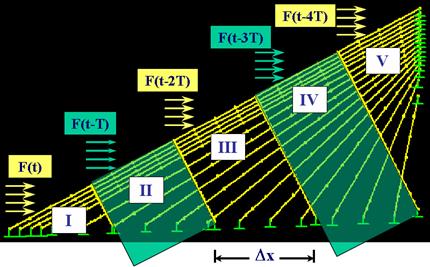
Figure 100 . Illustration. Sequential wind loading scheme.
PERFORMANCE UNDER REFERENCE WIND LOAD
In order to assess the performance of stay cable systems under applied wind loads, displacements computed at selected locations were retrieved and compared. Figure 101 shows displacement profiles computed at the mid-span of the longest cable of the stay systems under the reference wind load (wind-1). Four different crosstie designs (no crossties, one line of crossties, two lines of crossties, and four lines of crossties) were considered. The displacements, Ux, are the horizontal components parallel to the bridge axis.
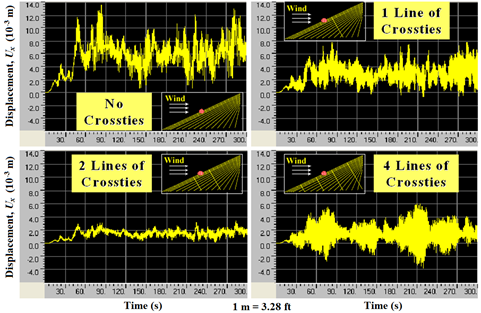
Figure 101 . Graph. Displacement computed at the mid-span of cable 1 with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
Among the four cases considered, the system with two lines of crossties produced the least displacement. However, the behavior may depend on the location where displacements were retrieved. Figure 102 through figure 104 show the displacement profiles computed at other locations within the system: at a quarter-span of the longest cable (figure 102), at the network center (figure 103), and at the mid-span of the shortest cable (figure 104). At a quarter-span, the system with four lines of crossties had the least displacement, while at the network center, the system with two lines of crossties had the least displacement. It is difficult to judge the mitigation effectiveness of a crosstied cable network simply by looking at displacements at some selected locations. Instead, mechanical energies of a system can be used as a global indicator of the performance, as will be discussed later.
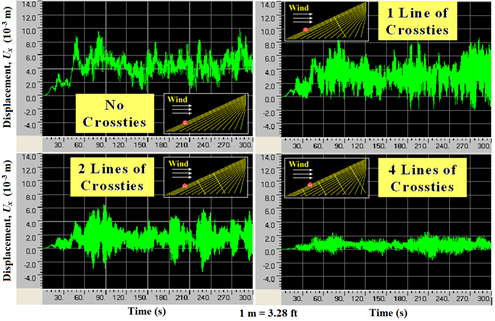
Figure 102 . Graph. Displacement computed at the quarter-span of cable 1 with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
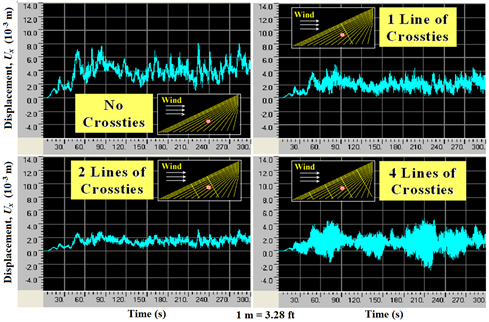
Figure 103 . Graph. Displacement computed at the center of the network with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
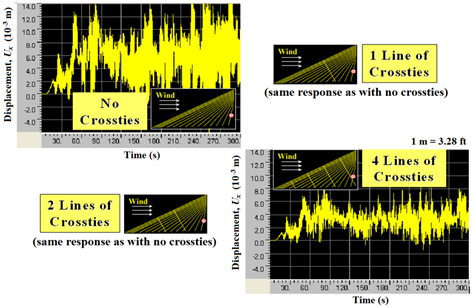
Figure 104 . Graph. Displacement computed at the mid-span of cable 16 (the shortest cable) with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
Displacement profiles in figure 101 and figure 102 were transformed into power spectral density (PSD) distributions in the frequency domain. Figure 105 shows the PSD distributions of the displacements at the mid-span of cable 1 (the longest cable) for the four different crosstying schemes considered. The graphs indicate that at the mid-span of the cable, displacement primarily takes place in the first mode of vibration of the networked cable system. The frequencies corresponding to maximum displacement PSDs coincide with the fundamental natural frequencies of the system, which indicates that a stay system responds in the first few fundamental modes to a normal wind loading.
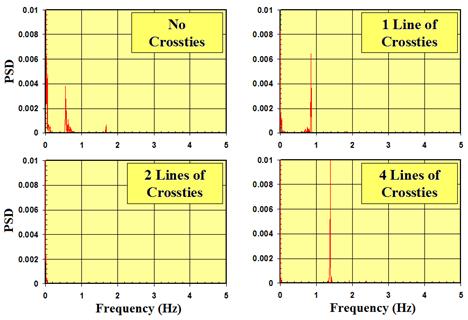
Figure 105 . Graph. PSD of the displacement at the mid-span of cable 1 with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
The fundamental (i.e., first mode) natural frequency of the system with no crossties, one line of crossties, two lines of crossties, and four lines of crossties are 0.56, 0.87, 1.18, and 1.38 Hz, respectively. For the system without crossties, the first-mode frequency of the system coincides with the first mode frequency of the longest cable. The system with two lines of crossties exhibited small displacement (figure 101), and the corresponding PSD was negligibly small compared to other three cases considered (figure 105). Note the large static value (f = 0 Hz) registered for the case of no crossties and very limited static component for the system with four lines of crossties.
Figure 106 show PSD distributions of the displacements at the quarter-span of cable 1 for the same four crosstying schemes considered. Again, the largest PSD occurred at the first mode of each system; however, additional peaks appeared at the second and third mode frequencies. A large-value PSD was registered at the fundamental mode for the two-line system.
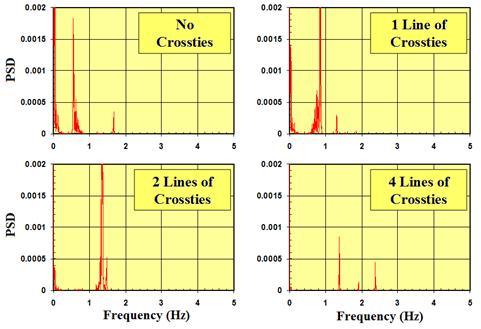
Figure 106 . Graph. PSD of the displacement at the quarter-span of cable 1 with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
Displacement responses retrieved at selected locations within a cable system were observed in an effort to assess the effectiveness of crossties in mitigating stay cable vibrations. However, it is difficult to view displacements as representing the overall structural performance of a stay system. A displacement profile gives information about the structural performance at a particular point in a system rather than the whole system. The level of a mechanical energy is often used to indicate the mechanical state of a system. Therefore, the evolution of mechanical energies of an entire cable system, not just of a single cable, is traced to assess the performance of the system. Figure 107 indicates the evolution of potential and kinetic energies of stay systems with different crosstying schemes.
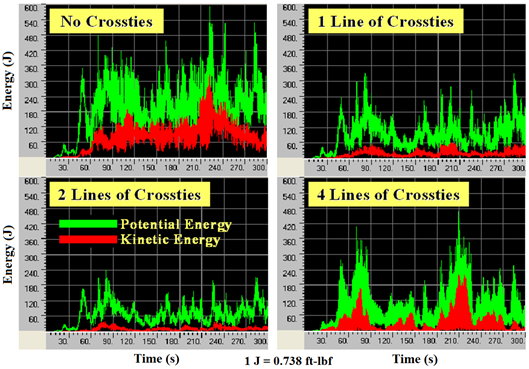
Figure 107 . Graph. Energy evolution of the cable system with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
In general, crossties are shown to effectively reduce both the potential and kinetic energies of a system, which can be interpreted as a reduced vibration. The potential energy is an indicator of the mean square of displacement amplitudes, and the kinetic energy is an indicator of the mean square of velocity amplitudes. A system with two lines of crossties renders the least energies of all. In this particular example, a system with four lines of crossties induces more energy than the two-line system and even than the one-line system. The performance of a crosstied system depends on the nature of the input wind profile used. Heavily crosstied systems tend to induce large vibrations when subjected to wind forces that contain appreciable high-frequency components.
PERFORMANCE UNDER OTHER WIND LOADS
In the previous section, the performance of a stay cable system with different crosstying schemes was examined by subjecting the system to the reference wind profile. The findings thus obtained may well depend on the type of input wind profiles. For this reason, a number of wind profiles, different from the reference, were considered. Relative performance of crosstied cable networks under these additional wind profiles were investigated and discussed.
In addition to the reference wind profile (wind-1), four other profiles, as shown in figure 108, were used in subsequent analysis. Two of the profiles, wind-2 and wind-3, are based on wind data recorded on the site. These profiles represent a 5-min wind speed record measured at the Bill Emerson Memorial Bridge in Cape Girardeau, MO. The profile is scaled up such that the peak 3-s gust speed reached 98 ft/s (30 m/s). In order to prevent an erroneous oscillation due to sudden impact loading at the beginning of an analysis, an artificial ramp was added for t = 0 to 10 s as for the wind-1 profile. The frequency-amplitude spectrum of wind-2 and wind-3 are shown in figure 109. Wind-3 has a quite different spectrum from those of wind-1 and wind-2 and contains large near-static low-frequency components.
The other two profiles, high frequency (wind-hf) and resonance (wind-res), are based on wind-1 with some modifications applied. In the frequency domain, wind-hf is the same as wind-1 except that the amplitudes for f = 1 Hz and above are doubled. Again, in the frequency domain, wind-res is the same as wind-1 except that an artificial amplitude spike of 50 is added at the fundamental natural frequency (1.38 Hz) of the cable network. These are clearly reflected in the frequency-amplitude spectrum shown in figure 109 for wind-hf and wind-res.
The purpose of using the wind-hf profile was to test the vulnerability of a crosstied cable network to wind loading containing enhanced high-frequency components. Use of crossties increases the natural frequencies of a cable system, which allows the system to effectively filter the low-frequency components of the wind. However, the performance of the same system under high-frequency (more turbulent) wind should be checked for design purposes. The wind-res profile is designed to test the vulnerability of the system to resonant vibrations with the input wind.
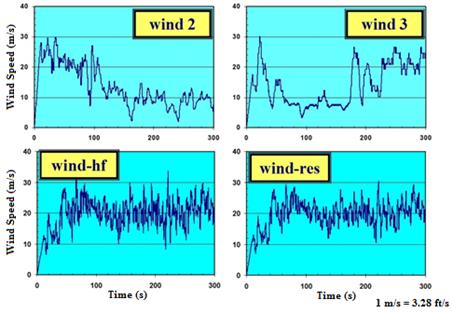
Figure 108 . Graph. Other wind speed profiles used-wind-2, wind-3, wind-hf, and wind-res.
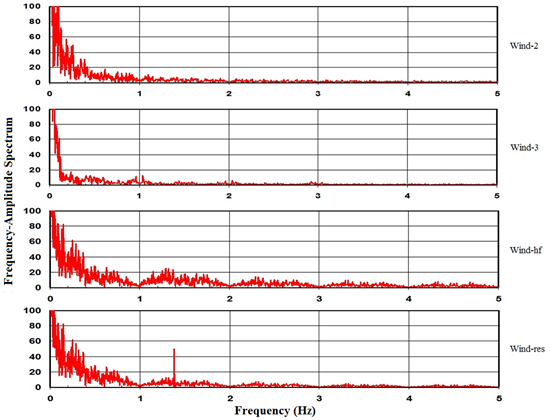
Figure 109 . Graph. Frequency-amplitude spectra of the wind profiles used-wind-2, wind-3, wind-hf, and wind-res.
Displacement time-histories at the mid-span of cable 1 when the cable system was subjected to wind-2 are presented in figure 110 for the four different crosstying schemes. It can be seen that the use of crossties greatly reduced cable vibrations. Energy evolution under wind-2 is shown in figure 111. Both displacement and energy evolution data indicate that a system with two lines of crossties best mitigates cable vibrations induced by wind-2. The four-line system appears to be effective in controlling static displacements but not quite in controlling vibration amplitudes.
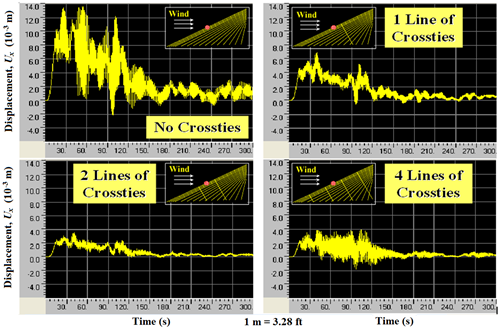
Figure 110 . Graph. Displacement computed at the mid-span of cable 1 when the cable network is subjected to wind-2 with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
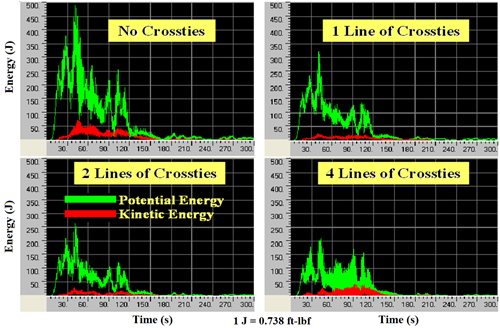
Figure 111. Graph. Energy evolution of the cable system subjected to wind-2 with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
Responses of the cable systems to wind-3 are presented in figure 112 for mid-span displacements and in figure 113 for energy evolutions. Both sets of figures indicate that the influence of crossties on reducing cable vibrations is significant. Displacement as well as potential and kinetic energy levels decreased dramatically. The four-line crosstie system exhibits the lowest energy levels among the four cases considered. The wind-3 profile is characterized by large low-frequency components. The four-line system, with its highest natural frequencies, is most effective to deal with low-frequency dominant winds.
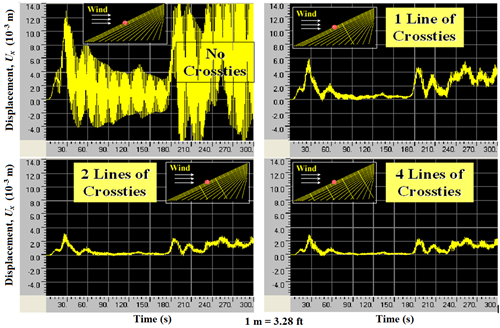
Figure 112 . Graph. Displacement computed at the mid-span of cable 1 when the cable network is subjected to wind-3 with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
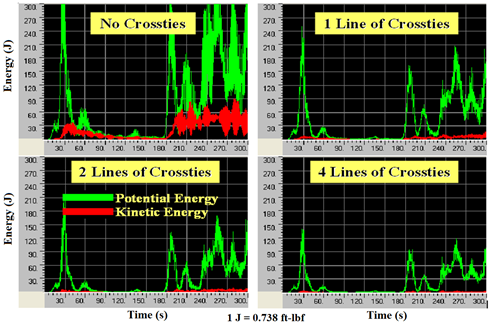
Figure 113 . Graph. Energy evolution of the cable system subjected to wind-3 with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
Displacements under wind-hf are shown in figure 114, and energy evolutions under wind-hf are shown in figure 115. It is clear that the mitigation effectiveness of crossties significantly decreased when the system was subjected to high-frequency enhanced wind. Benefits of the use of crossties appear to be proportional to the quantity of crossties to a certain degree. However, further increases in crosstie quantity resulted in increased magnitudes of cable vibration. Under an artificial profile, wind-hf, the performance of a cable system gradually improved up until the two-line system. However, for the four-line system, the performance became worse. The four-line system clearly shows its response sensitivity to high-frequency wind components.
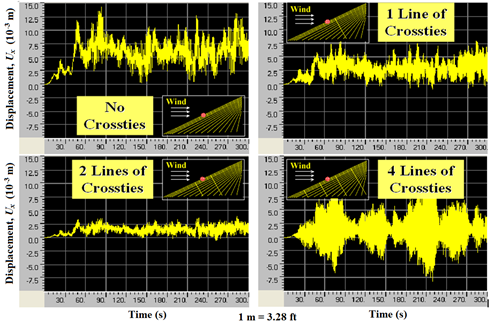
Figure 114 . Graph. Displacement computed at the mid-span of cable 1 when the cable network is subjected to wind-hf with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
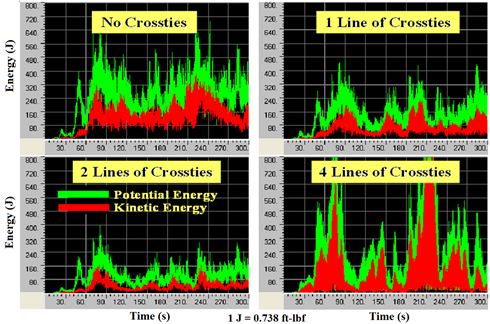
Figure 115 . Graph. Energy evolution of the cable system subjected to wind-hf with no crossties, one line of crossties, two lines of crossties, and four lines of crossties.
In general, the results suggest that the use of crossties helps mitigate wind-induced stay cable vibrations. However, as the quantity of crossties increases beyond a certain threshold, the system becomes more vulnerable to high-frequency components of winds. Therefore, the performance of a crosstied network is sensitive to the frequency content of wind loading. Crossties are particularly effective in reducing low-frequency components of cable vibrations. Performance of a crosstied network is not necessarily proportional to its quantity (or number of lines) of crossties. An excessive provision of crossties may result in an adverse effect under highly turbulent winds (if present).
The displacement of a cable system with four lines of crossties subjected to wind-1 and wind-res at the mid-span of cable 1 are shown in figure 116. Figure 117 shows the PSD distributions of the displacement profiles shown in figure 116. A noticeable peak is present at the resonant frequency (f = 1.38 Hz) of the system when the system is subjected to wind-res. Energy evolution, which is presented in figure 118, confirms the fact that a system responds sensitively to a wind load containing a finite amplitude at the system's resonant frequency.
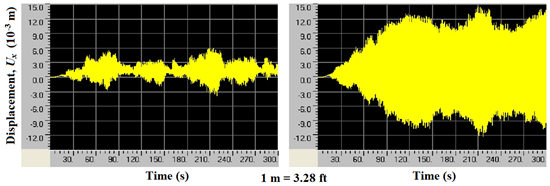
Figure 116 . Graph. Displacement at the mid-span of cable 1 when the cable network with four lines of crossties is subjected to wind-1 (left) and wind-res (right).
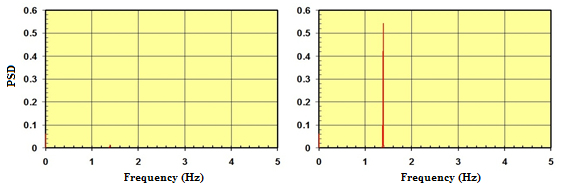
Figure 117 . Graph. PSD of the displacement at the mid-span of cable 1 when the cable network with four lines of crossties is subjected to wind-1 (left) and wind-res (right).
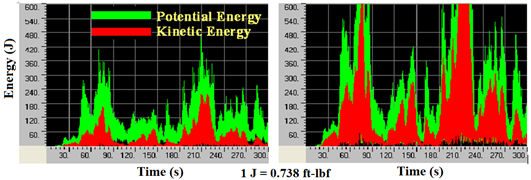
Figure 118 . Graph. Energy evolution of the cable network with four lines of crossties subjected to wind-1 (left) and wind-res (right).
It can be seen that a slight magnification of the wind component at the resonant frequency of the input wind load results in a dramatically magnified response of the system, which indicates the vulnerability of a cable system to resonant wind loading. The system quickly builds up a resonant vibration with its limited inherent damping. The addition of dampers may effectively lower the potential of such occurrence.
Peak axial force distribution in cables and crossties is presented in figure 119. Particular attention was given to the compressive forces in the crossties to see if they were within the pre-tension levels. The axial forces shown do not include pre-tensions applied to the cables and crossties during construction. The maximum peak compressive force in the crossties was 5.2 kip (23 kN), which is within the applied pre-tension level of 7.9 kip (35 kN). This insures that the crossties remain taut throughout the event. The pre-tension level required to prevent the slack of the crossties depends on the severity of the design wind event.
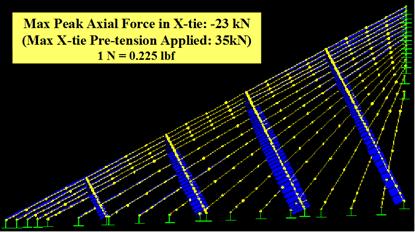
Figure 119 . Image. Peak axial force distribution under wind-1.
Peak shear force distribution in cables and crossties is shown in figure 120. Since cables and crossties are modeled as beams with transverse stiffnesses, they carry shear forces. Largest shear forces are experienced at the cable supports and at the cable/crosstie junctions, which must be taken into account in design of a crosstying system.
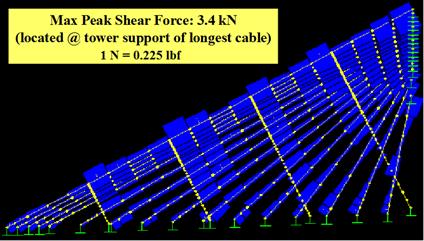
Figure 120 . Image. Peak shear force distribution under wind-1.