U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-14-049 Date: August 2014 |
Publication Number: FHWA-HRT-14-049 Date: August 2014 |
The in-plane stiffness of stay cables increases when they are connected by means of a set of transverse cables referred to as "crossties." Crossties have been introduced over the past several decades as a means of counteracting large-amplitude vibrations of the stays in cable-stayed bridges. Crossties are also known to reduce the cable sag variations among stay cables of various lengths.(11) From the dynamics point of view, the presence of lateral constraints modifies the oscillation characteristics of the stay group. Also, the interconnection of individual stay cables results in a complex cable network. As a result, a closed-form solution to a structural analysis problem of such network is elusive.
A number of studies on crossties for stay cables have been conducted. (See references 9, 10, 12, and 13). However, the dynamic behavior of a stay cable system networked with crossties is still not clearly understood, and the effectiveness of crossties is not well established. In this study, the effectiveness of crossties in mitigation of stay cable vibrations was numerically investigated. Both modal analyses and time-history analyses were conducted on a set of stay cables from the recently completed Bill Emerson Memorial Bridge in Cape Girardeau, MO. The modal (i.e., free-vibration) analysis is discussed later in this chapter. The time-history (i.e., forced-vibration) analysis under transient wind loads is discussed in chapter 5.
Numerical analysis was conducted using the general purpose finite element code SAP2000®.(8) An elevation view of the subject bridge is shown in figure 57 with the cables under study circled in blue. The bridge has two H-shaped towers supporting 128 stays. The main span of the bridge is 1,148 ft (350 m) long, and two side spans are each 468 ft (143 m) long. The finite element discretization of a side section of stay cables is shown in figure 58. Four parallel lines of crossties perpendicular to the longest cable and equally dividing this cable into five segments are considered as the reference configuration. A few other configurations of crossties are also considered later for comparison purposes. The basic information on the bridge, as provided by the designer, is presented in table 1. Data on cable-end coordinates and cable properties are presented in table 2 and table 3.
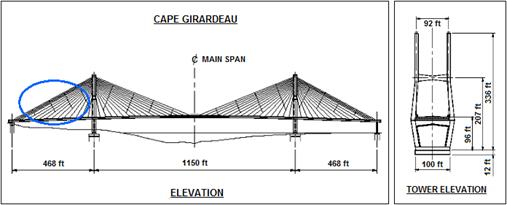
Figure 57 . Illustration. Bill Emerson Memorial Bridge in Cape Girardeau, MO.
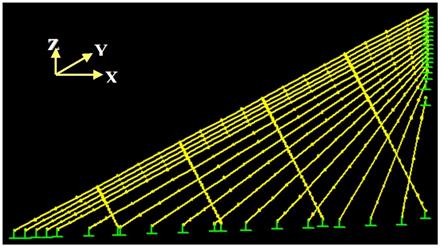
Figure 58 . Image. Finite element discretization of a cable system with four lines of crossties.
Table 1 . Basic information on the Bill Emerson Memorial Bridge.
Bridge Name |
Cape Girardeau/Bill Emerson Memorial |
Owner |
State of Missouri |
Designer |
HNTB |
Year Design Completed |
1996 |
Year Construction Completed |
2003 |
Superstructure Type |
Steel composite |
Superstructure Width |
96 ft (29.26 m) |
Tower Type |
H-shaped |
Main Span Length |
1,150 ft (350.52 m) |
Side Span Length |
468 ft (142.65 m) |
Number of Stays |
128 |
Number of Stay Planes |
2 |
Cable Type |
Seven-wire strand |
Strand Diameter |
0.62 inch (1.52 cm) |
Grout |
Cement |
Outer Sheathing |
High-density polyethylene |
Supplemental UV Protection |
None |
Number of Cross Tie Lines-Side Span |
4 |
Number of Cross Tie Lines-Main Span |
4 |
Crosstie Diameter |
0.81 inch (2.06 cm) |
Supplemental Damper |
Neoprene |
Damper Location |
Both ends |
Table 2 . Coordinates of cable ends on the Bill Emerson Memorial Bridge.
Cable Number |
Tower-End |
Tower-End |
Deck-End |
Deck-End |
|---|---|---|---|---|
1 |
-5.77 |
310.3 |
-460.6 |
66.0 |
2 |
-5.77 |
305.3 |
-448.6 |
66.5 |
3 |
-5.77 |
300.3 |
-436.6 |
66.9 |
4 |
-5.77 |
295.3 |
-424.7 |
67.3 |
5 |
-5.77 |
290.2 |
-413.1 |
67.6 |
6 |
-5.74 |
285.3 |
-378.4 |
68.8 |
7 |
-5.67 |
280.4 |
-343.8 |
70.0 |
8 |
-5.64 |
275.4 |
-309.2 |
71.3 |
9 |
-5.67 |
270.5 |
-274.8 |
72.5 |
10 |
-5.61 |
265.6 |
-240.3 |
73.7 |
11 |
-5.61 |
260.7 |
-205.8 |
75.0 |
12 |
-5.97 |
255.4 |
-171.3 |
76.3 |
13 |
-6.04 |
249.4 |
-137.1 |
77.4 |
14 |
-6.04 |
242.7 |
-102.7 |
78.7 |
15 |
-7.71 |
230.8 |
-68.4 |
79.9 |
16 |
-7.77 |
213.5 |
-34.1 |
81.4 |
1 ft = 0.305 m
Table 3 . Cable properties on the Bill Emerson Memorial Bridge.
Cable |
Chord |
Outer |
Young's |
Cable |
Mass |
Unit |
Unit Weight |
Frequency |
|---|---|---|---|---|---|---|---|---|
1 |
516.3 |
10.75 |
2.261 |
1019.6 |
162.1 |
162.1 |
102.1 |
0.549 |
2 |
503.1 |
10.75 |
2.261 |
1069.4 |
162.1 |
162.1 |
102.1 |
0.577 |
3 |
490.0 |
10.75 |
2.180 |
1019.6 |
159.0 |
159.0 |
100.1 |
0.584 |
4 |
476.9 |
8.62 |
2.768 |
979.6 |
172.7 |
172.7 |
70.0 |
0.703 |
5 |
464.2 |
8.62 |
2.621 |
935.5 |
170.5 |
170.5 |
69.1 |
0.711 |
6 |
431.0 |
8.62 |
2.523 |
901.3 |
168.0 |
168.0 |
68.1 |
0.758 |
7 |
398.2 |
8.62 |
2.425 |
855.5 |
168.0 |
168.0 |
68.1 |
0.799 |
8 |
365.8 |
8.62 |
2.425 |
827.4 |
168.0 |
168.0 |
68.1 |
0.855 |
9 |
334.1 |
7.12 |
3.564 |
735.3 |
180.6 |
180.6 |
50.0 |
1.029 |
10 |
303.1 |
7.12 |
3.444 |
672.4 |
177.0 |
177.0 |
49.0 |
1.095 |
11 |
273.1 |
7.12 |
3.324 |
636.4 |
173.4 |
173.4 |
48.0 |
1.196 |
12 |
243.7 |
7.12 |
3.204 |
591.2 |
169.8 |
169.8 |
47.0 |
1.305 |
13 |
216.3 |
6.61 |
2.789 |
561.3 |
171.9 |
171.9 |
41.0 |
1.534 |
14 |
190.3 |
6.61 |
2.468 |
463.1 |
167.7 |
167.7 |
40.0 |
1.603 |
15 |
169.1 |
6.61 |
2.307 |
409.2 |
163.5 |
163.5 |
39.0 |
1.718 |
16 |
147.7 |
6.61 |
2.227 |
380.2 |
163.5 |
163.5 |
39.0 |
1.894 |
1 ft = 0.305 m
1 inch = 25.4 mm
1 psi = 6.89 kPa
1 kip = 4.45 kN
1 lbm/ft3 = 16.0 kg/m3
1 lbf/ft3 = 0.157 kN/m3
1 lbf/ft = 0.0146 kN/m
The stay cables and crossties are modeled using the beam elements with their flexural stiffness. The pre-tension forces in stay cables and crossties are modeled using P-delta forces. The cable ends are assumed to be fixed to the deck and to the tower. Both the deck and the tower are assumed to be immobile relative to the stays for simplicity, and no parametric motion between the stays and the deck or tower is considered. Analysis is also focused on the in-plane motion of the stay system, with the out-of-plane motion being treated as an exception.
NATURAL FREQUENCIES AND MODE SHAPES
Free-vibration analysis of a structural system provides information on the system's intrinsic vibration characteristics commonly expressed in terms of natural frequencies and the corresponding mode shapes. A set of homogeneous dynamic equilibrium equations for a system leads to an eigenvalue problem in which the eigenvalues are identified as the system's natural vibration frequencies and the corresponding eigenvectors as the mode shapes. A change in structural condition causes changes in the natural frequencies and mode shapes. Therefore, the influence of crossties on the vibration characteristics of a stay cable system may be explored by observing the mode-frequency evolution of the system.
Figure 59 shows the first four in-plane vibration mode shapes and the corresponding natural frequencies, Fi, for a stay cable system with four lines of crossties. The first three modes are global in nature in that the large portion of the cable system participates in the motion. Local modes set in at the fourth mode and prevailed in subsequent modes. The next four modes, which are highly local in nature, are shown in figure 60. Some sample higher modes for n = 20–23 are presented in figure 61. These higher modes are characterized by localized vibration of cable segments divided by crossties. A local mode is governed by the geometry of internal elements of the system and is characterized by wavelengths corresponding to the distances between neighboring crossties.
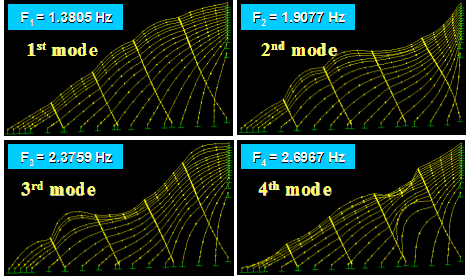
Figure 59 . Image. In-plane vibration mode shapes 1–4 of a stay cable system with four lines of crossties.
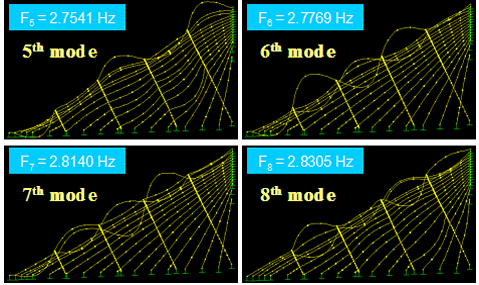
Figure 60 . Image. Vibration mode shapes 5–8 of a stay cable system with four lines of crossties.
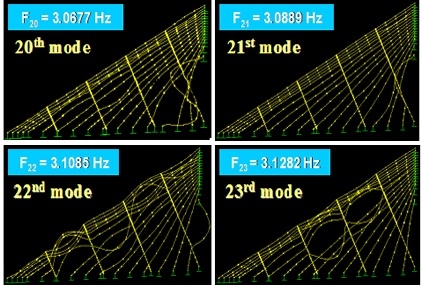
Figure 61 . Image. Vibration mode shapes 20–23 of a stay cable system with four lines of crossties.
The so-called "mode-frequency evolution" chart for a crosstied cable network (see figure 58) is presented in figure 62. The abscissa denotes the mode numbers and the ordinate the system's natural frequencies. A similar approach was used by Abdel-Ghaffar and Khalifa and Caracoglia and Jones.(10,14) It is clear that incorporation of crossties into a stay system increases its natural frequencies for all modes. The first few modes, which are global in nature, are followed by a long series of local modes whose natural frequencies are densely populated over a narrow band of frequency. The solid triangle in figure 62 denotes the fundamental (n = 1) natural frequency of the longest cable, and the diamond that of the shortest cable. Note that the fundamental natural frequency of the crosstied system is bracketed between those of the longest and shortest cables.
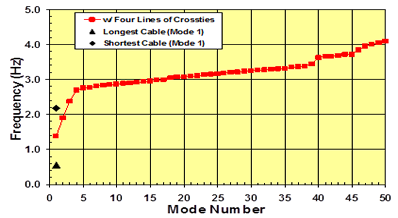
Figure 62 . Graph. Mode-frequency evolution for a stay cable system with four lines of crossties.
Different design parameters that influence the mitigation effectiveness of a crosstied cable system was tested through finite element simulations. Specifically, the mode-frequency evolution characteristics are examined in detail.
INFLUENCE OF CROSSTIE QUANTITY
First, the influence of crosstie quantity (or the influence of the number of lines of crossties) on the system's mode-frequency evolution behavior was studied. Figure 63 shows the finite element discretization of a cable system with two lines of crossties. Figure 64 and figure 65 show the first four and some intermediate (n = 20–23) mode shapes and the corresponding natural frequencies for this system. In figure 66, the mode-frequency evolution for this system is presented in comparison with that of the reference system with four lines of crossties. It can be seen that the two line-system exhibits lower natural frequencies than the four-line system especially for n = 4–23. It is to be noted that local vibration modes set in right after the fundamental mode (i.e., n = 2) for the two-line system.
Figure 63 . Image. Finite element discretization of a cable system with two lines of crossties.
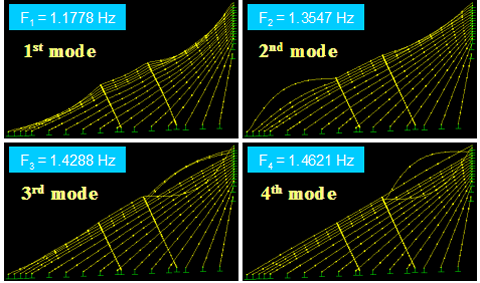
Figure 64 . Image. Vibration mode shapes 1–4 of a stay cable system with two lines of crossties.
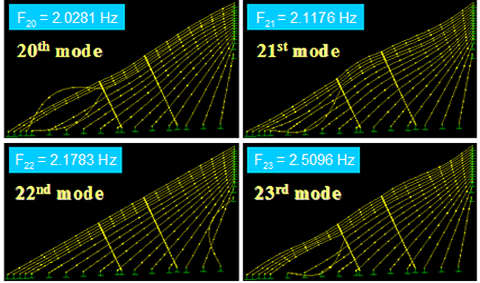
Figure 65 . Image. Vibration mode shapes 20–23 of a stay cable system with two lines of crossties.
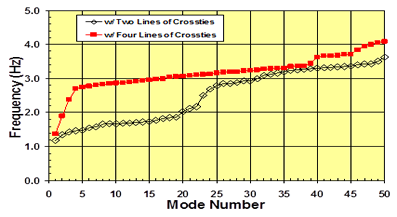
Figure 66 . Graph. Mode-frequency evolution for a stay cable system with two lines of crossties.
Figure 67 shows the finite element discretization of a cable system with a single line of crossties. Figure 68 and figure 69 show the first four and some intermediate mode shapes (n = 20–23) and the corresponding natural frequencies for this system. The system's mode-frequency evolution behavior is shown in figure 70. Again, the behavior of the reference (four-line) system is presented for comparison. The one-line system exhibits much lower natural frequencies than the reference system. It is difficult to distinguish global modes from local modes, and local modes appear to set in at the very first mode.
Figure 67 . Image. Finite element discretization of a cable system with one line of crossties.
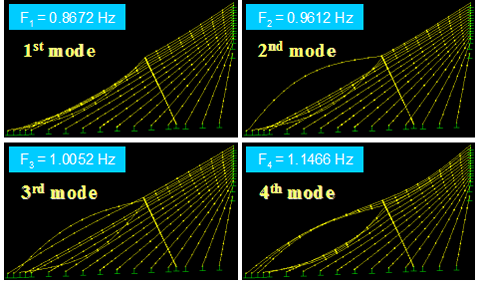
Figure 68 . Image. Vibration mode shapes 1–4 of a stay cable system with one line of crossties.
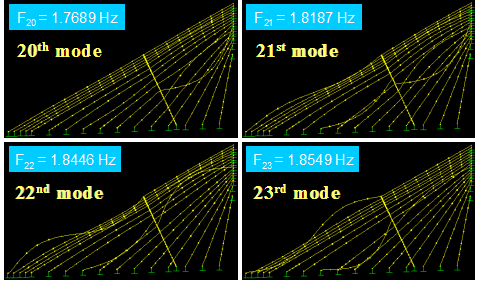
Figure 69 . Image. Vibration mode shapes 20–23 of a stay cable system with one line of crossties.
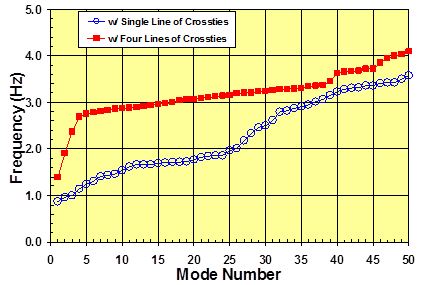
Figure 70 . Graph. Mode-frequency evolution for a stay cable system with one line of crossties.
A cable system without any crossties was also considered, and its finite element discretization is shown in figure 71. The first four mode shapes and some intermediate mode shapes (n = 20–23) for this system are shown in figure 72 and figure 73. For a cable system without crossties, the natural modes of the system consist of the natural modes of the individual cables. The first few system modes correspond to the fundamental modes of individual cables. However, at some point, higher modes of long cables begin to interlace with lower modes of short cables. The mode-frequency evolution behavior is shown in figure 74 along with that of the reference four-line system. Again, the efficiency of crossties in terms of enhancing the system's natural frequencies is evident. The presence of step jumps in mode-frequency chart, which is characteristics of crosstied cable systems, is not seen in the case of the non-crosstied system.
Figure 71 . Image. Finite element discretization of a cable system with no crossties.
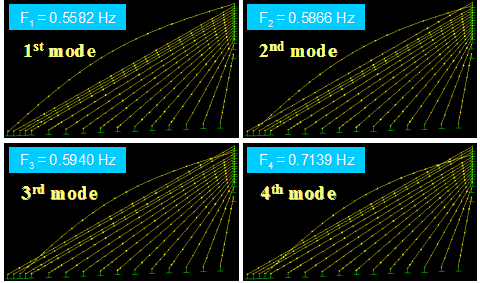
Figure 72 . Image. Vibration mode shapes 1–4 of a stay cable system with no crossties.
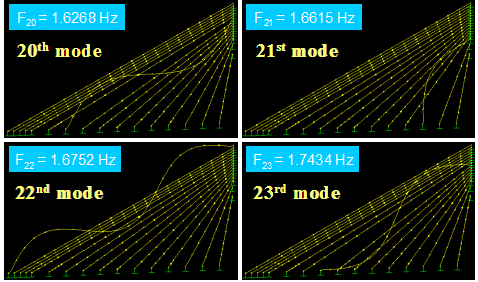
Figure 73 . Image. Vibration mode shapes 20–23 of a stay cable system with no crossties.
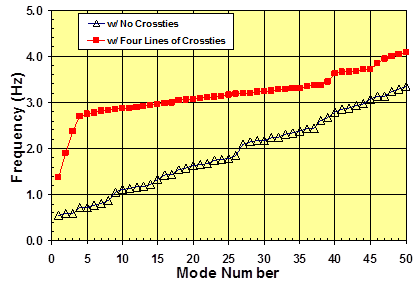
Figure 74 . Graph. Mode-frequency evolution for a stay cable system with no crossties.
Another simulation was conducted with nine lines of crossties. Figure 75 shows the finite element discretization of a cable system with nine parallel lines of crossties. Figure 76 and figure 77 show the mode shapes for this system, n = 1–4 and n = 20–23. The mode-frequency evolution is presented in figure 78 as a comparison to the reference system. Distinction between global and local modes is clear; however, modes up to n = 25 generally engage a large portion of the segments and thus may be global in nature. A plateau of densely populated local modes appears at a much higher mode compared to the reference four-line system.
Figure 75 . Image. Finite element discretization of a cable system with nine lines of crossties.
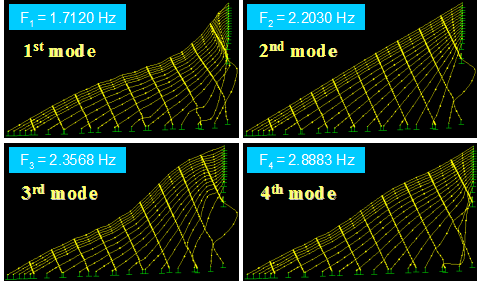
Figure 76 . Image. Vibration mode shapes 1–4 of a stay cable system with nine lines of crossties.
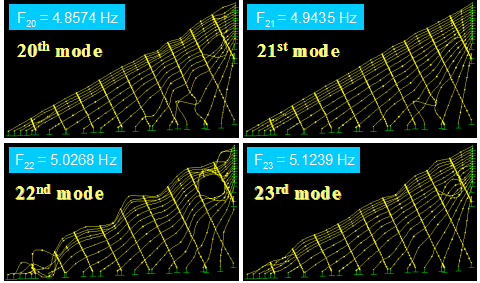
Figure 77 . Image. Vibration mode shapes 20–23 of a stay cable system with nine lines of crossties.
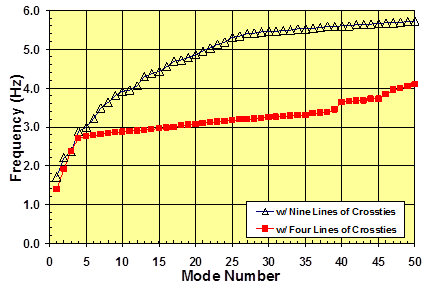
Figure 78 . Graph. Mode-frequency evolution for a stay cable system with nine lines of crossties.
A comparison summary is presented in figure 79. Systems with zero, one, two, four, and nine lines of crossties are compared with respect to their mode-frequency evolution characteristics. Clearly, increasing the amount of crossties increases the natural vibration frequencies of the system, although the details of the increase pattern depend on the geometry of the crossties.
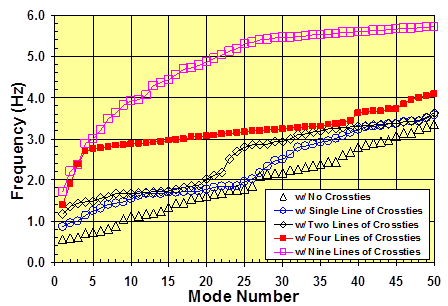
Figure 79 . Graph. Comparison of the mode-frequency evolutions of a stay cable system with differing quantities of crossties.
INFLUENCE OF CROSSTIE GEOMETRY
The mitigation effectiveness of crossties should depend on the way the crossties are arranged for a given quantity. For example, figure 80 shows a cable system with eight zigzag lines of crossties, and figure 81 and figure 82 show selected mode shapes and the corresponding natural frequencies for this system. The first three modes are global in nature. The quantity of crossties of this system is comparable to that of the nine-line system shown in figure 75. The total cumulative length of crossties in the two cases in figure 75 and figure 80 are 994 and 1,063 ft (303 and 324 m), respectively. The quantity of the eight zigzag lines of crossties is slightly greater than that of the nine-line crossties.
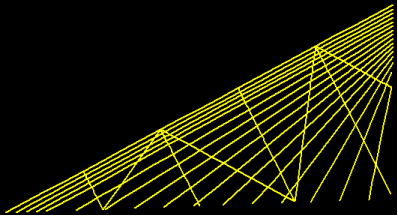
Figure 80 . Image. Finite element discretization of a cable system with eight zigzag lines of crossties.
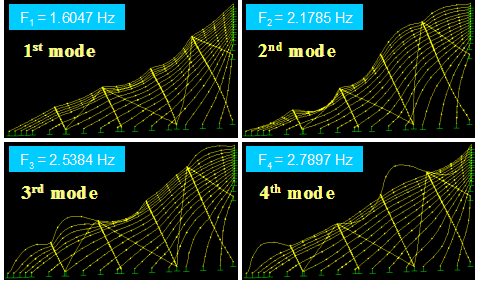
Figure 81 . Image. Vibration mode shapes 1–4 of a stay cable system with eight zigzag lines of crossties.
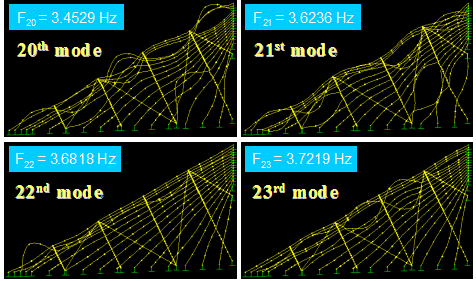
Figure 82 . Image. Vibration mode shapes 20–23 of a stay cable system with eight zigzag lines of crossties.
The mode-frequency evolution for this system is presented in figure 83. Also presented for comparison are those for the four-line and the eight-line systems. For comparable crosstie quantities, the straight-line (nine lines) system yields much higher natural frequencies than the zigzag (eight lines) system, especially at higher modes (i.e., n > 5). Note that the zigzag arrangement constitutes a larger quantity than the straight-line arrangement. It can also be seen that the straight line arrangement shifts the band of densely populated local modes to a much higher mode.
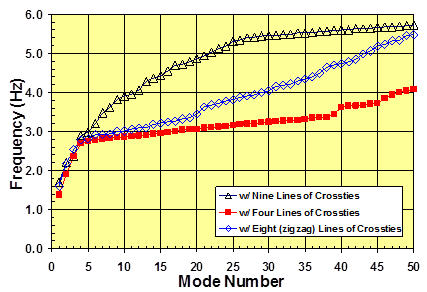
Figure 83 . Graph. Mode-frequency evolution for a stay cable system with crossties of differing geometry.
A system with a single crosstie line intersecting the stay cables at their mid-span was also considered (see figure 84) for comparison with a single straight-line system (see figure 67). Selected mode shapes and frequencies are shown in figure 85 and figure 86. The mode-frequency evolution for this system is compared with those for the straight single-line crosstie and reference four-line crossties, as shown in figure 87. The straight single-line crosstie has a fundamental natural frequency (n = 1) slightly higher than that of the curved crosstie; however, overall, no appreciable difference can be observed between the two systems.
Figure 84 . Image. Finite element discretization of a cable system with one line of crossties interconnecting the midpoints of the cables.
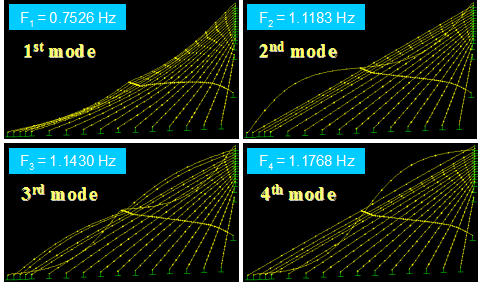
Figure 85 . Image. Vibration mode shapes 1–4 of a stay cable system with one line of crossties interconnecting the cable midpoints.
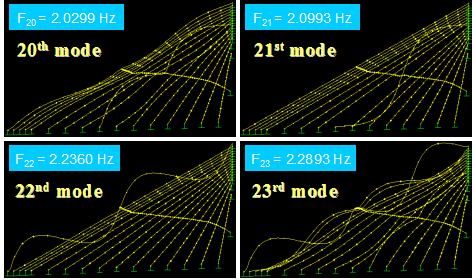
Figure 86 . Image. Vibration mode shapes 20–23 of a stay cable system with one line of crossties interconnecting the cable midpoints.
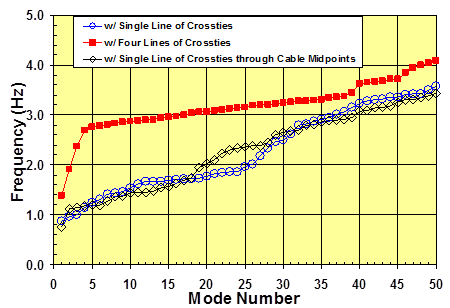
Figure 87 . Graph. Mode-frequency evolution for a stay cable system with one line of crossties of differing geometry.
INFLUENCE OF CROSSTIE DIAMETER
The influence of crosstie size (or diameter) on the in-plane vibration behavior of a crosstied stay system was investigated. Figure 88 shows fundamental vibration modes (n = 1) for a four-line system with different crosstie diameters that are 0.5, 1.0, 2.0, and 10.0 times the diameter of the reference crosstie. The mode-frequency evolutions for these four different cases are presented in figure 89.
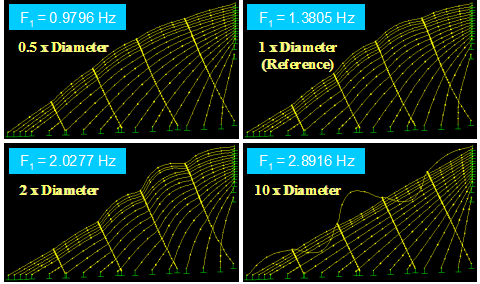
Figure 88 . Image. Fundamental vibration mode of a stay cable system with four lines of crossties of differing diameter.
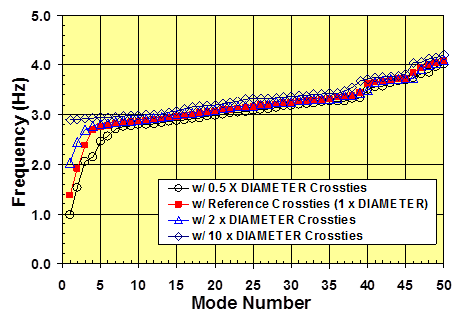
Figure 89 . Graph. Mode-frequency evolution for a stay cable system with four lines of crossties of differing diameter.
Increasing the diameter of the crosstie increased the natural frequencies of the system up to a certain limit beyond which no appreciable increases take place. It can be seen that oversized crossties tend to render the system to be overly rigid and susceptible to local mode vibrations, which are potentially undesirable. The case with 10 times the reference diameter approximates a case of perfectly rigid crossties, and only localized vibration modes are allowed to take place in this extreme case.
Influences of other design parameters, such as crosstie anchorage conditions, stay cable end conditions, and crosstie pretension level, on the mode-frequency behavior of a stay cable system were also investigated.
Figure 90 shows a cable network with crossties not anchored to the deck, and the mode-frequency behavior of this system is shown in figure 91. For comparison, the mode-frequency evolution of the reference system in which the crossties are anchored is also shown in figure 91. It can be seen that anchoring (or grounding) the crossties to the deck increases the overall stiffness of the system, thus increasing the natural frequencies of the system. The increase is most pronounced for the first few modes which are global in nature. The impact of crosstie anchorage on the localized vibration modes is minimal. Grounded crossties enhance the frequencies of global modes by more than 30 percent in the case shown.
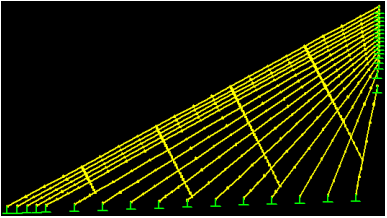
Figure 90 . Image. Finite element discretization of a cable system with four lines of crossties not anchored to the deck.
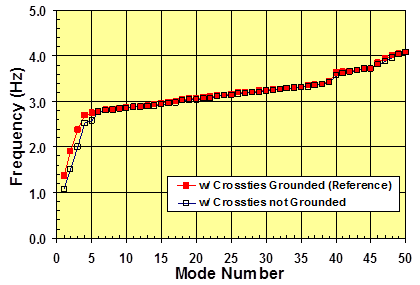
Figure 91 . Graph. Effect of crosstie anchorage (to the deck) on the mode-frequency evolution of a stay cable system with four lines of crossties.
Figure 92 shows the influence of stay cable end conditions on the modal characteristics of a cable network. The figure shows that end conditions, whether fixed or hinged, do not affect the system's modal behavior that much, except for very high vibration modes. As the mode number increases, the vibration wavelength becomes shorter, and the cable support conditions become increasingly significant.
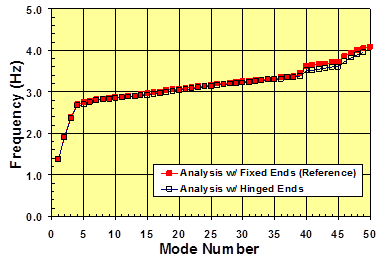
Figure 92 . Graph. Effect of cable end conditions on the mode-frequency evolution of a stay cable system with four lines of crossties.
Figure 93 shows the sensitivity of the mode-frequency behavior of a system to pre-tension level in the crossties. The open circles denote the case of reference tension level, while the small closed circles denote the case of 10 times the reference pre-tension level. The two lines shown practically overlap entirely, and virtually no influence of pre-tension level can be observed. Pre-tension affects the transverse (or flexural) stiffness of crossties and the in-plane vibration of a cable network is not much sensitive to the transverse stiffness of crossties. However, crossties must be provided with appropriate levels of pre-tension to prevent slack of the crossties during design wind events. The analysis showed that as long as adequate levels of pre-tension are maintained, the pre-tension does not affect the system's in-plane vibration behavior. Conversely, the transverse (i.e., out-of-plane) vibration is affected significantly by the pre-tension level, as is discussed in the following section.
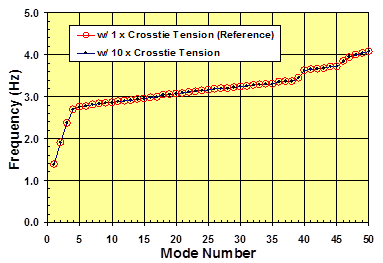
Figure 93 . Graph. Effect of crosstie tension on the mode-frequency evolution of a stay cable system with four lines of crossties.
It is well known that crossties are not effective in mitigation of out-of-plane vibration of stay cables due to their limited flexural stiffnesses. This fact and other related issues were verified through finite element analysis. The first four transverse vibration mode shapes and natural frequencies are presented in figure 94. Although crossties are not primarily designed to counteract the transverse vibrations of stay cables, they still provide some limited constraints to transverse vibrations.
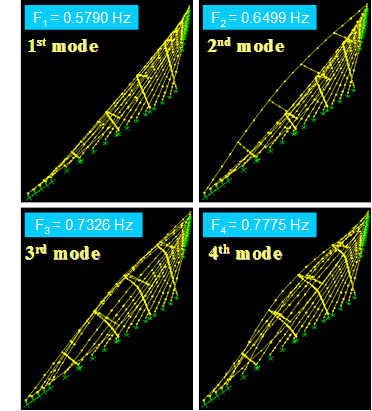
Figure 94 . Image. Transverse vibration mode shapes 1–4 of a stay cable system with four lines of crossties.
Figure 95 compares the transverse mode-frequency behavior of stay systems with and without crossties. It confirms the notion that crossties are ineffective in providing transverse constraints to a crosstied cable network. Very limited increases in natural frequency were observed. Figure 96 shows the influence of pre-tension level in crossties on the transverse vibration of stays. While the pre-tension level practically does not affect the in-plane behavior, it affects the out-of-plane behavior. Increased pre-tension leads to increased system frequency, which can be understood from the fact that increased pre-tension increases the flexural stiffness of the system.
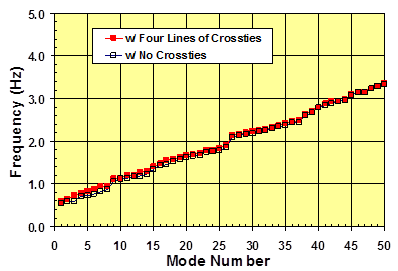
Figure 95 . Graph. Transverse mode-frequency evolution for a stay cable system with and without crossties.
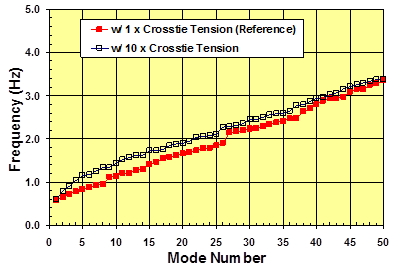
Figure 96 . Graph. Effect of cable tension on the transverse mode-frequency evolution for a stay cable system with four lines of crossties.