U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000

Skip to content
Facebook iconYouTube iconTwitter iconFlickr iconLinkedInInstagram

Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations

 
REPORT
This report is an archived publication and may contain dated technical, contact, and link information
Back to Publication List        
Publication Number:  FHWA-HRT-14-049    Date:  August 2014
Publication Number: FHWA-HRT-14-049
Date: August 2014

 

Mitigation of Wind-Induced Vibration of Stay Cables: Numerical Simulations and Evaluations

CHAPTER 6: TIME-HISTORY ANALYSIS OF STAY CABLES WITH EXTERNAL DAMPERS

INTRODUCTION

Dampers are frequently used to suppress excessive vibration of stay cables which have limited intrinsic damping. These dampers, due to practical limitations of installation, are usually attached to the stay cables near the anchorages. Although theories behind the observed behavior of stays with attached dampers are not completely developed, dampers have been widely used, and their effectiveness has been demonstrated by many examples. Application of dampers for cable vibration mitigation is anticipated to be more widespread, and the need for improved understanding of the resulting dynamic system is increasing. The effectiveness of different strategies involving external dampers and crossties for mitigation of stay cable vibrations is investigated via finite element simulations.

CONFIGURATION AND DAMPER COEFFICIENT

Figure 121 shows a single stay with a viscous damper attached near the anchorage. The distance of the damper from the deck anchorage is 2 percent of the chord length of the cable (d = 0.02 L). The stay simulates Cable SWC-01 of the Cape Girardeau Bridge, whose properties are presented in table 2 and table 3 (see cable 1). A sequential wind loading on the cable is shown in figure 122, in which F(t) denotes the horizontal wind force history shown in figure 99.

This image shows a schematic representation of a stay cable with a viscous damper attached to it. The length of the cable is denoted as L, and the offset distance of the damper from the deck is denoted as d. Also included in the figure is a note saying that the offset distance of the damper is 0.02 times the cable length.
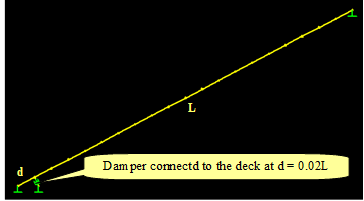
Figure 121 . Image. Stay cable with a viscous damper attached to it.

This image shows sequential wind loading on a stay cable used in the current study. The cable is divided into five zones, and each zone is exposed to wind loading in a sequential manner with finite time intervals. The time interval, denoted as T, is estimated by dividing the horizontal traverse distance of the wind by the average wind speed.
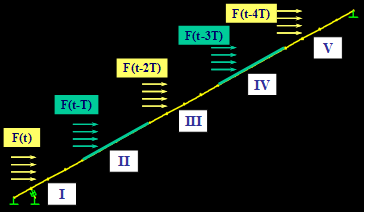
Figure 122 . Image. Sequential wind loading on the cable.

The optimal damping coefficient (Copt) for the cable is determined from the universal damping curve shown in figure 123. This asymptotic analytical curve proposed by Krenk is valid when d/L, the relative damper distance from the support, is very small.(15)

This graph shows the universal damping curve used in determining the coefficients of external viscous dampers. The x-axis shows the normalized damping coefficient, denoted by kappa, ranging from 0 to 1.0. The y-axis shows the normalized damping ratio denoted by xi subscript i divided by open parenthesis d divided by L closed parenthesis, ranging from 0 to 0.6. The curve starts at the origin and rapidly rises and peaks at a value of 0.5 where kappa is 0.1, and then it continuously decreases with increasing kappa down to an approximate value of 0.1 where kappa approaches 1.0.
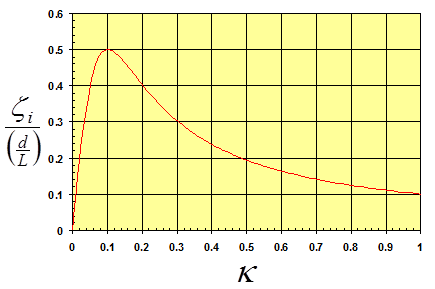
Figure 123 . Graph. Universal damping curve.

The curve relates the normalized damping ratio ζi/(d/L) to the normalized damping coefficient (κ) defined as follows:

Kappa is defined as C divided by m times L times omega subscript 1 times i times open parenthesis d divided by L closed parenthesis.
Figure 124 . Equation. Normalized damping coefficient.

Where:

C = Damper coefficient.
m = Cable mass per unit length.
ω1 = First mode natural frequency.
ζi = Damping ratio of the ith mode of vibration.
i = Mode number.

At optimal damping, the normalized damping ratio reaches 0.5 and κ approaches 0.1, from which C-values are determined for different modes. The achievable modal damping ratios are limited by this relationship. For example, for d/L of 2 percent, the achievable maximum damping ratio for the first mode is 1 percent.

RESPONSE TO REFERENCE WIND LOAD

Figure 125 and figure 126 show the horizontal components of the displacement histories computed at the mid- and quarter-span of the stay without and with a damper, respectively. It can be seen that the use of a damper reduces the vibration amplitudes of the stay. Figure 127 shows the energy evolution of the stay without and with a damper, respectively. Both the potential and kinetic energies are reduced due to the incorporation of a damper; however, the reduction of kinetic energy is more pronounced than that of potential energy. When damper is not used, the energy of the cable is dissipated entirely by intrinsic modal damping. A uniform modal damping of 0.3 percent is assumed. When a damper is used, the majority of the energy is dissipated via the damper, and only a small fraction of the energy is dissipated via intrinsic damping of the cable.

This graph shows displacement computed at the mid-span of a stay cable without a damper (left) and with damper (right). The x-axis shows time ranging from 0 to 300 s, and the y-axis shows displacement ranging from 0 to 4.92×10-2 ft (0 to 15.0×10-3 m). The displacement shown is the horizontal component parallel to the bridge axis, and the cable is subjected to the reference wind profile. A cable with an external damper shows slightly reduced displacement response compared to that with no damper.
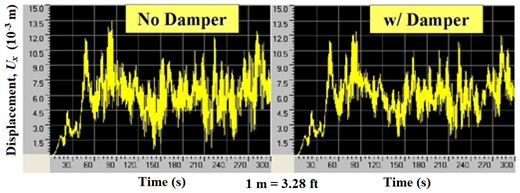
Figure 125 . Graph. Displacement computed at mid-span of the cable without damper (left) and with damper (right).

This graph shows displacement computed at the quarter-span of a stay cable without a damper (left) and with a damper (right). The x-axis shows time ranging from 0 to 300 s, and the y-axis shows displacement ranging from 0 to 4.92×10-2 ft (0 to 15.0×10-3 m). The displacement shown is the horizontal component parallel to the bridge axis, and the cable is subjected to the reference wind profile. A cable with an external damper shows reduced displacement response compared to that with no damper.
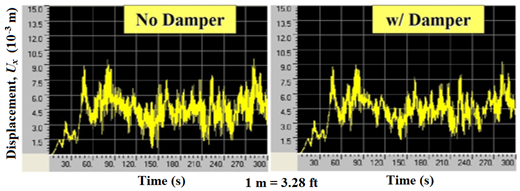
Figure 126 . Graph. Displacement computed at quarter-span of the cable without damper (left) and with damper (right).

This graph shows the evolution of mechanical energies of a stay cable without a damper (left) and with a damper (right) subject to the reference wind profile. The x-axis shows time ranging from 0 to 300 s, and the y-axis shows energy ranging from 0 to 36.9 ft-lbf (0 to 50 J). The potential energy is represented by a green line, the kinetic energy by a red line, the energy dissipation via cable's inherent damping by a blue line, and the energy dissipation via external damper by a yellow line. The potential energy is an indicator of the mean square of displacement amplitudes, and kinetic energy is an indicator of the mean square of velocity amplitudes in a vibration. For both plots, the potential and kinetic energy fluctuate rapidly with time, and energy dissipation gradually accumulates with time. For the cable without a damper, the amount of energy dissipated over 300 s via cable's inherent damping is about 16.6 ft-lbf (22.5 J). For the cable with a damper, the amount of energy dissipated over 300 s via cable's inherent damping is about 6.3 ft-lbf (8.5 J), and that via the external damper is about 17.0 ft-lbf (23 J).
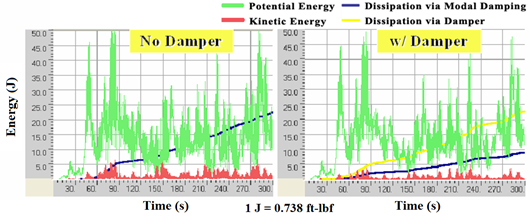
Figure 127 . Graph. Energy evolution of the cable without damper (left) and with damper (right).

Figure 128 and figure 129 show the PSD distributions for the displacement profiles computed at the mid- and quarter-span of the stay, respectively. Without damper, vibration took place primarily in the first and third modes, whereas when a damper was installed, the vibration was mostly in the first mode, and only a small trace in the third mode was observed. According to the theory, the use of a damper shifts the natural vibration frequencies of the stay; however, in this particular example, the amount of shift appears to be very limited.

This graph compares power spectral density (PSD) distributions for displacements computed at the mid-span of a stay cable without a damper (left) to that with a damper (right) subject to the reference wind profile, wind-1. The x-axis shows frequency ranging from 0 to 5 Hz, and the y-axis shows PSD ranging from 0 to 0.007. Distinctive peaks are seen at the first and third natural frequencies of the cable (0.55 and 1.67 Hz, respectively) without a damper. A reduced peak was observed at the first natural frequency of the cable, and negligibly small value is registered at the third natural frequency for the cable with a damper. Overall, the cable with a damper exhibits reduced PSD compared to that without a damper.
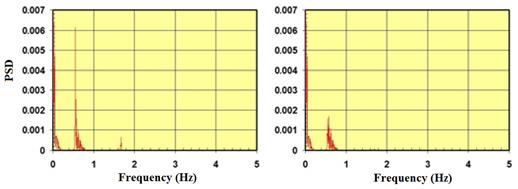
Figure 128 . Graph. PSD for displacement at mid-span of the cable without damper (left) and with damper (right).

This graph shows power spectral density (PSD) distributions for displacement computed at the quarter-span of a stay cable without a damper (left) compared to a stay cable with a damper (right) subject to the reference wind profile. The x-axis shows frequency ranging from 0 to 5 Hz, and the y-axis shows PSD ranging from 0 to 0.003. For the cable without a damper, distinctive peaks are seen at the first and third natural frequencies of the cable (0.55 and 1.67 Hz, respectively). A reduced peak was observed at the first natural frequency of the cable with a damper, and negligibly small value is registered at the third natural frequency. Overall, the cable with a damper exhibits reduced spectral density compared to that without a damper.
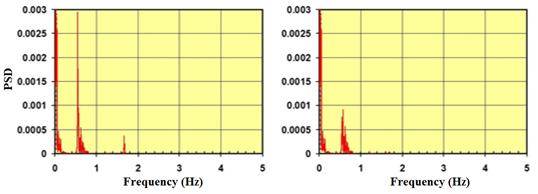
Figure 129 . Graph. PSD for displacement at quarter-span of the cable without damper (left) and with damper (right).

Figure 130 shows the energy evolution of a single cable without and with a damper subjected to wind-hf. The effectiveness of the use of a damper is more pronounced when a stay is subjected to a wind event that contains enriched high-frequency components. In other words, dampers are more efficient in mitigating stay vibrations containing appreciable high-frequency components. The major portion of the vibration energy is dissipated via the damper. It is to be noted that dampers are effective in mitigating transverse and in-plane vibrations when separate dampers are installed in the respective directions of motion.

This graph shows the evolution of mechanical energies of a stay cable without a damper (left) compared to a stay cable with a damper (right) subject to wind-high frequency (hf). The x-axis shows time ranging from 0 to 300 s, and the y-axis shows energy ranging from 0 to 36.9 ft-lbf (0 to 50 J). The potential energy is represented by a green line, the kinetic energy by a red line, the energy dissipation via cable's inherent damping by a blue line, and the energy dissipation via external damper by a yellow line. For both plots, the potential and kinetic energy fluctuate rapidly with time, and energy dissipation gradually accumulates over time. For a cable without a damper, the amount of energy dissipated over 210 s via the cable's inherent damping is about 31.0 ft-lbf (42 J). For a cable with a damper, the amount of energy dissipated over 300 s via the cable's inherent damping is about 14.8 ft-lbf (20 J), and that via the external damper is about 35.4 ft-lbf (48 J).
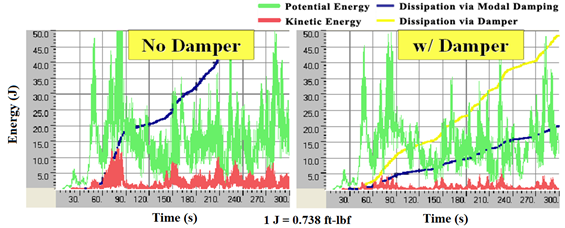
Figure 130 . Graph. Energy evolution of the cable under wind-hf without damper (left) and with damper (right).

INFLUENCE OF DAMPER PARAMETERS

The efficiency of a damper depends primarily on its damping coefficient and its location on the stay, among other factors. In order to test the influence of damping coefficient (or damper coefficient), four different levels of damping were considered: C = 0 (no damper), C = Copt, C = 0.1 Copt, and C = 10 Copt. Results are shown in figure 131, which highlights the evolution of the potential and kinetic energy of a cable/damper system subjected to wind-1. Also shown are energies dissipated through intrinsic modal damping and through the damper.

This graph shows the evolution of mechanical energies of a stay cable with zero damping, optimal damping (Copt), 0.1 times Copt, and 10 times Copt. The cable is subject to the reference wind profile, wind-1. The x-axis shows time ranging from 0 to 300 s, and the y-axis shows energy ranging from 0 to 36.9 ft-lbf (0 to 50 J). The potential energy is represented by a green line, the kinetic energy by a red line, the energy dissipation via cable's inherent damping by a blue line, and the energy dissipation via external damper by a yellow line. For all plots, the potential and kinetic energy fluctuate rapidly with time, and energy dissipation gradually accumulates over time. Among the four cases studied, the case of Copt (case b) mitigates the cable vibration most effectively, which is manifested by the largest energy dissipation via damper. In the case of Copt, the amount of energy dissipated over 300 s via cable's inherent damping is about 6.6 ft-lbf (9 J), and that via the external damper is about 17 ft-lbf (23 J).
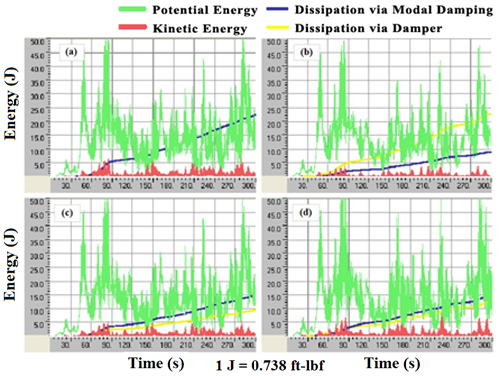
Figure 131 . Graph. Energy evolution of the cable when different levels of damper coefficient are used—(a) C = 0 (no damper), (b) C = Copt, (c) C = 0.1 Copt, and (d) C = 10 Copt.

As can be expected, the cable performed best when the damper had its optimal coefficient, C = Copt. Energy levels, especially kinetic energy, are lowest when the optimal value is used. It can be seen that with the optimal damper coefficient (see graph b in figure 131), the amount of energy dissipated through the damper is greatest, and the demand of energy dissipation through the cable's intrinsic modal damping is minimal. Dissipation by modal damping is proportional to kinetic energy due to their dependence on velocity. Therefore, less dissipation by modal damping signifies a lower level of kinetic energy, meaning lesser cable vibrations.

To test the influence of damper location, four different cases were considered. Figure 132 shows results for C = 0 (no damper), d/L = 0.02, d/L = 0.05, and d/L = 0.10, where d is the offset distance of the damper from anchorage, and L is the chord length of the stay cable. The case of d/L = 0.10 gives the largest energy dissipation through the damper, and the achieved kinetic energy level is lowest among the four cases considered, signifying its being the most effective in vibration mitigation. However, due to practical limitations associated with installation, dampers are usually attached to stays near the anchorages.

This graph shows the evolution of mechanical energies of a stay cable with zero damping, with a damper offset 0.02 times the cable length, 0.05 times the cable length, and 0.10 times the cable length, where d is the offset distance of the damper from the anchorage, and L is the chord length of the stay cable. The cable is subject to the reference wind profile, wind-1. The x-axis shows time ranging from 0 to 300 s, and the y-axis shows energy ranging from 0 to 36.9 ft-lbf (0 to 50 J). The potential energy is represented by a green line, the kinetic energy by a red line, the energy dissipation via cable's inherent damping by a blue line, and the energy dissipation via external damper by a yellow line. For all plots, the potential and kinetic energy fluctuate rapidly with time, and energy dissipation gradually accumulates over time. Among the four cases studied, an offset distance of 0.1 times d/L mitigates the cable vibration most effectively, which is manifested by the largest energy dissipation via damper and lowest dissipation via cable damping. In the case of an offset distance of 0.1 times d/L, the amount of energy dissipated over 228 s via cable's inherent damping is about 36.9 ft-lbf (50 J), and that via the external damper over 300 s is about 4.4 ft-lbf (6 J).
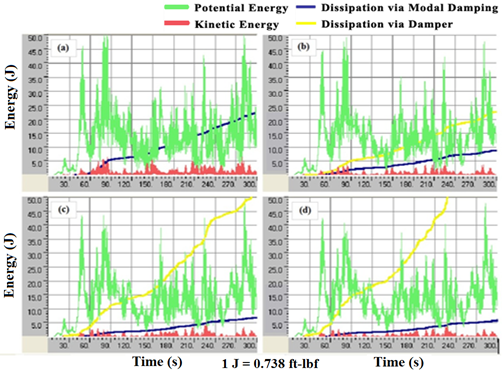
Figure 132 . Graph. Energy evolution of the cable when different damper locations are used—(a) C = 0 (no damper), (b) d/L = 0.02, (c) d/L = 0.05, and (d) d/L = 0.10.

 

Return to top

Privacy Policy | Freedom of Information Act (FOIA) | Accessibility | Web Policies & Notices | No Fear Act | Report Waste, Fraud and Abuse | U.S. DOT Home | USA.gov | WhiteHouse.gov

Federal Highway Administration | 1200 New Jersey Avenue, SE | Washington, DC 20590 | 202-366-4000
Turner-Fairbank Highway Research Center | 6300 Georgetown Pike | McLean, VA | 22101