U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-15-033 Date: May 2015 |
Publication Number: FHWA-HRT-15-033 Date: May 2015 |
The literature relevant to this research was reviewed and divided into three main categories: critical shear stress, erosion rates, and erosion testing devices. Design guidance has typically related to critical velocity, critical shear stress, and/or erosion rate. Critical velocity is defined as the velocity at which soil erosion is initiated. Similarly, critical shear stress is the shear stress at which the soil erosion is initiated. For cohesive soils, the ability to determine these values, and the erosion rates once they are exceeded, has been largely accomplished by various erosion testing devices.
Before 1955, critical velocity was used to determine whether cohesive soils would erode. During the 1950s, researchers moved to the critical shear stress of soils as a more direct indication of the erodibility of a particular soil because critical velocity depended on other hydraulic parameters.
A critical shear stress may be assigned to a specific cohesive soil. It was assumed that if the eroding shear stress exceeds the critical shear stress, then a soil will experience erosion. In this framework, critical shear stress is considered a soil property. Researchers attempted to correlate it to other soil properties as a means of predicting its value for a given soil. Dunn correlated the critical shear stress to soil vane shear strength, PI, and clay fraction (particles less than 0.0024 inches (0.060 mm)).(3) Smerdon and Beasley related critical shear stress to the PI, dispersion ratio, mean particle size of clay, and percentage of clay.(4,5) Several investigators proposed using a power law of bulk density to reflect the critical shear stress of a soil.(6,7)
Straub and Over found a linear relationship between soil critical shear stress and the logarithm of the unconfined compressive strength in undisturbed cohesive soils in Illinois.(8) In that work, the critical shear stresses of undisturbed field soils were extrapolated from erosion testing using the erosion function apparatus (EFA).
However, other researchers have stated that erosion in cohesive soils is essentially a surface phenomenon and should not be related to a bulk engineering properties such as unconfined compressive strength.(9) Previous studies have explored relations between erosion characteristics and properties such as vane shear strength, unconfined compressive strength, and dry unit weight but have not found useful relations. (See references 10 through 13.)
Some researchers argued that the critical shear stress definition is arbitrary because different observers would interpret different thresholds for critical shear stress. In addition, it was thought that the critical shear stress would also be affected by the flow condition. For example, identical soils experiencing open channel flow versus periodic flow like ocean waves would have different critical shear stresses.
In addition to these challenges, determining the critical shear stress for a particular soil does not equip a design engineer with information about erosion rates once the critical shear stress is exceeded. Knowing the critical shear stress also does not provide information on the spatial extent of erosion. Erosion rates and erosion spatial properties also vary based on the flow conditions.
The erosion rate is defined by both the flow condition and the soil properties. Most research concerning erosion rates to date has focused on surficial marine sediments or soft muds that have a wet bulk density between 31 to 81 lb/ft3 (500 to 1,300 kg/m3).(14,15) In some of these conditions, the water content (the ratio of water mass to soil mass) is equal to or larger than 100 percent. Depending on the apparatus and test methods used, only a limited depth of surficial mud might be tested. The wet bulk density of bottom mud can increase to 110 lb/ft3 (1,800 kg/m3) because of consolidation.
For these kinds of soils, researchers proposed two erosion formulations: linear law and exponential law. The linear law is written in the form seen in figure 7.(16)
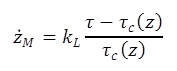
Figure 7. Equation. Linear erosion law of cohesive soils
Where:
![]() M = Mass erosion rate, lb/ft2/s (g/m2/s).
M = Mass erosion rate, lb/ft2/s (g/m2/s).
kL = Empirical erosion constant, lb/ft2/s (g/m2/s).
𝜏 = Hydraulic shear stress, lbf/ft2 (Pa).
𝜏c(z) = Critical shear stress at a depth of z, lbf/ft2 (Pa).
z = Depth from soil surface, inches (mm).
The exponential law has the form seen in figure 8:
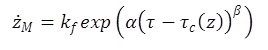
Figure 8. Equation. Exponential erosion law of cohesive soils
Where:
kf = Empirical floc erosion rate, lb/ft2/s (g/m2/s).
α, β = Empirical constants.
Mehta and Partheniades divided erosion test results into Type I and II based on the erosion profile and the change in shear stress applied to the soil.(17) In both cases, an erosion profile with increasing shear resistance with soil depth is assumed. The difference between the two types of erosion is defined by the relative time scale of the shear stress applied to the soil compared with the depletion (or erosion) time scale of the soil. Type I behavior is observed when the time scale of the shear stress is long compared with the time scale of the soil depletion. This case is referred to as depth limited erosion, in which an exponential decay in the erosion rate is experienced. The equation in figure 8 is used for this type. Type II behavior is observed when the time scale of the shear stress is short compared with the time scale of the soil depletion. This case is referred to as unlimited erosion, in which a linear increase in the erosion rate is experienced. The equation in figure 7 is used for this type.(18)
Researchers have developed several devices to study scour in cohesive soils by measuring the forces involved in the scour process. Moore and Masch developed a circular Couette flow erosion device (CCFED).(19) The device provides a stationary mount attached to a torsion wire for a circular soil specimen. An outer drum, concentric with the soil specimen, contains the eroding fluid between it and the soil specimen. The outer drum is rotated by a variable speed motor, and a shear stress is consequently transmitted to the soil specimen surface, which can be directly measured by knowing the angular displacement of the torsion wire. The erosion rate of cohesive sediments is determined from the loss of mass within the testing time interval.
Other apparatus have been proposed to estimate critical shear stress in cohesive soils. These devices include the following:
Trammell detailed the motivation, testing procedures, data analysis, advantages, and limitations of the ASSET, EFA, SEDflume, and SERF devices.(26) The following discussion focuses on the description of HET and JET to provide a range of the types of devices available.
For the HET, a clay specimen is inserted into a confining tube connecting two water tanks with different water levels. A pinhole is bored in the center of the specimen. Water flows through the pinhole, exerting shear stress to erode the specimen. The flow velocity is increased steadily until entrainment occurs. At the end of each time increment, the eroded outflow is collected to obtain the erosion rate, and the average diameter of the enlarged hole is calculated. The shear stress is estimated from the head loss between the two tanks. For this computation, the friction coefficient can be obtained from the Moody chart. An erosion curve (erosion rate versus shear stress) is plotted and then fit to the equation seen in figure 9.(24)
![]()
Figure 9. Equation. Wan and Fell equation for cohesive soil erosion
Where:
![]() M = Mass erosion rate, lb/ft2/s (g/m2/s).
M = Mass erosion rate, lb/ft2/s (g/m2/s).
k = Slope of the erosion curve, dimensionless.
𝜏 = Hydraulic shear stress along the hole, lbf/ft2 (Pa).
𝜏c = Critical shear stress for the initiation of erosion, lbf/ft2 (Pa).
For the JET, sediment is placed in the bottom of an open tank. An adjustable constant-head tank supplies water to a vertical tube submerged in the open tank, creating an impinging jet of water on the sediment. By converting potential energy to kinetic energy, the jet obtains a certain velocity to erode the sediments. The jet nozzle typically has a diameter of 0.25 inches (6.4 mm). The nozzle height above the soil surface can be adjusted in a range of 1.6 to 8.7 inches (40 to 220 mm). After the test time period, a point gage with the equivalent diameter of the nozzle is inserted in the tube to shut off the jet and measure the erosion depth. The instantaneous shear stress is calculated using the equation in figure 10.(27)
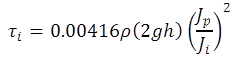
Figure 10. Equation. Instantaneous shear stress equation for a jet
Where:
𝜏i = Instantaneous peak boundary shear stress, lbf/ft2 (Pa).
ρ = Fluid density, lb/ft3, (kg/m3).
g = Acceleration due to gravity, 32.2 ft/s2 (9.81 m/s2).
h = Nozzle height above the soil surface, ft (m).
JP = Potential jet core length (taken as 6.3 times the jet nozzle diameter), ft (m).
Ji = Instantaneous jet orifice height, ft (m).
The critical shear stress is determined by plotting the measured values of Ji and 𝜏i. Because the equilibrium scour depth is not reached within the test period, it is extrapolated from the measured data. The shear stress is then calculated for that depth from the equation in figure 10. From these data, the critical shear stress can be calculated.
Although each device measures soil erosion in some manner, they differ regarding the types of erosion that is being measured in the following ways:
Different flow conditions generate distinct dynamic forces on tested cohesive soils. For bridge safety design, a device that can simulate the log-law flow condition in open channels is urgently needed. The reproduced log-law flow condition generates similar hydrodynamic forces, meaning that the erosion process in open channels can be reproduced.