U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-054 Date: October 2017 |
Publication Number: FHWA-HRT-17-054 Date: October 2017 |
Local scour at bridge piers and abutments is a potential safety hazard of major concern to transportation agencies. If scour at a bridge pier or abutment can adversely affect the stability of a bridge, scour countermeasures to protect the bridge should be considered. Rock riprap is a common countermeasure used to prevent or reduce scour. While the Federal Highway Administration (FHWA) does not recommend riprap as a design countermeasure for piers on new bridges, it can be used for new bridge abutments. Rock riprap can also be used as a remedial measure for scour at piers and abutments for existing bridges.
Current riprap design methodologies and scour evaluation procedures provide a threshold size of rock that is anticipated to be stable under a pre-determined design condition. These methods are intended to be conservative in order to be useful for a wide variety of field conditions.
The sizing of riprap in scour countermeasure design procedures is based primarily on limited field observations and scaled laboratory tests under controlled conditions. FHWA’s Hydraulic Engineering Circular No. 23 (HEC-23) Bridge Scour and Stream Instability Countermeasures, Experience, Selection, and Design Guidelines includes a formula that is functionally equivalent to the 1936 Isbash formula that provides a median rock size (D50) based on the water depth (y) at the pier and the Froude number (Fr).(1) The HEC-23 formula includes a multiplicative factor on the mean velocity intended to account for higher instantaneous velocities resulting from increased turbulence intensity for pier shapes that are not simple cylinders.
However, because riprap sizing formulas are based on limited data, there is uncertainty and variation in the equations for sizing riprap. For example, there is a large spread in the design median rock size using formulas for piers proposed between 1973 and 1999. A comparison based on work by Lagasse et al. is summarized in figure 1.(2) As is apparent in the figure, most equations yield larger values than the HEC-23 approach.
The methods also do not provide a site-specific understanding of when rocks might become displaced especially if the stream morphology or hydrology has changed from the time of design. Therefore, advanced computational mechanics techniques might offer benefits for the assessment and design of rock riprap and to ascertain the scour vulnerability of existing bridges.
The analysis of riprap stability can be considered a fluid structure interaction (FSI) problem. FSI problems involve solving for the fluid flow force on a solid surface, the response of that solid to the load, and subsequently the change of the flow conditions caused by displacement of the solid. Computational fluid dynamics (CFD) software is used for solving fluid flows and computational structural mechanics (CSM) software used is used for solving the deformations and stresses in solid bodies.
Historically, CFD and CSM have developed independently. In recent years, both have been developing additional solvers needed for FSI problems. However, at the moment, there is no integrated software package with both highly robust CSM and CFD solvers needed for general purpose FSI analyses. The current best practice is to couple highly reliable independent CFD and CSM software in an iterative analysis that requires exchange of data on common interfaces between the fluid and solid structures at small time intervals.
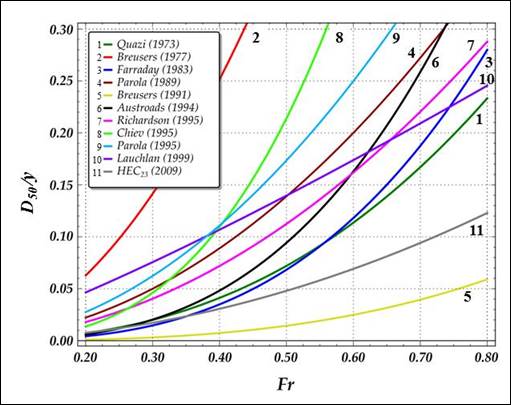
Source: Modified by FHWA from NCHRP report 568. See Acknowledgment page. *
Figure 1. Graph. Comparison of riprap sizing curves at a rectangular pier.
*Revised 10/17/18
The STAR-CCM+ CFD software from the Computational Dynamics-Analysis and Design Application Company (CD-Adapco) is capable of solving flow problems in domains containing solid objects with complex, irregular geometry in relative motion along arbitrary paths through the fluid domain.(3) The LS-DYNA CSM software from the Livermore Software Technology Company (LSTC) is a general purpose finite element program capable of simulating highly non-linear real world problems in structural mechanics with changing boundary conditions (such as contact forces between rocks that change over time), large displacements, large deformations, and non-linear material property relations.(4) These were coupled for this study to analyze the stability of rock riprap under varying geomorphic and hydraulic conditions.
The objectives of this research study were as follows:
These objectives were addressed in this project through a combination of physical and numerical modeling. The numerical modeling was then tested and validated on a field case study.
Chapter 2 provides an overview of the literature review conducted to support this project. Chapter 3 describes physical modeling used to validate the numerical modeling. Chapters 4 and 5 summarize the development of the coupled FSI numerical modeling tool and its application to a field case study. Conclusions and recommendations are provided in chapter 6.
Two appendices provide detailed background information for the interested reader: appendix A provides the annotated bibliography developed during the literature search and appendix B provides additional technical information on the development and testing of the coupled FSI numerical modeling tool.