U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-054 Date: October 2017 |
Publication Number: FHWA-HRT-17-054 Date: October 2017 |
The numerical modeling approach described in chapter 4 was applied to a complex field case study to evaluate the potential for such a tool to evaluate and to design riprap protection for bridge piers and abutments. Current design methodologies and scour evaluation procedures are often based on laboratory studies or straight forward field situations. This case study will illustrate the potential for use of advanced computational mechanics techniques to assess rock stability and bridge vulnerability.
The case study represents an opportunity to study the effectiveness of riprap installed to protect a bridge pier in Plumas County, California. The bridge carries State Route 89 over the Middle Fork of the Feather River near the towns of Blairsden and Graeagle. The bridge was built in 1955 and the river channel was realigned at the time to straighten the flow upstream of the bridge as shown in figure 24.
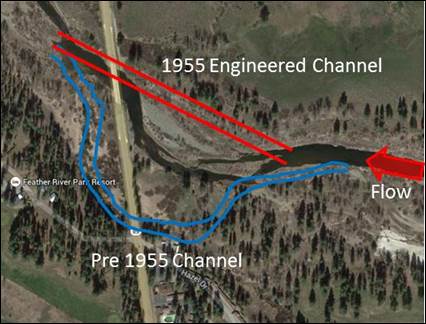
Figure 24. Photo. Historic, realigned, and current channel alignment.
During high winter flows in 1988, the river avulsed from its 1955 realignment and moved toward its historic streambed and flow path. As a result, the flow approaches the bridge at the sharp angle shown in figure 24, causing excessive backwater and deep scour at one of the piers.
Later, the California Department of Transportation (Caltrans) determined that the bridge was scour critical based on vertical contraction scour and local pier scour. In 2011, a field survey was conducted at the bridge site. The survey included acquisition of river bathymetry from a boat and Global Positioning System (GPS) coordinates of ground features near the bridge. The bathymetric survey was conducted using a SonarMite depth finder by Seafloor Systems. Figure 25 shows the riverbed elevation model built based on that data with the deepest scour in front of the pier of primary concern: pier 3.
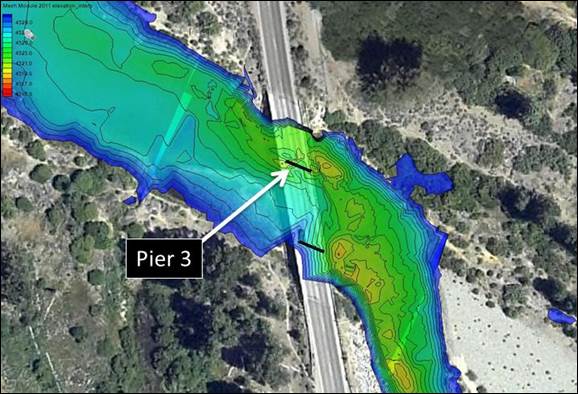
1 ft = 0.305 m
Figure 25. Photo. River bathymetry before installation of the riprap.
In August 2012, Caltrans placed rock riprap over filter fabric around the most vulnerable pier to protect the bridge. A 1-ton average rock size was specified for this work. Figure 26 shows the extent of the riprap apron design around pier 3. Figure 27 shows the work area near pier 3 during the riprap installation.
In 2013, Caltrans performed a follow-up riverbed survey. Reconstructed bathymetry based on this survey is shown in figure 28. The scour hole was completely leveled with the surrounding bed. However, subsequent investigation of the project site suggested that the riprap design velocities were underestimated and, therefore, the riprap may be under sized to withstand the 100-year design event.(11) This concern led to further analysis using the advanced numerical modeling developed for this research project and described in the following section.
The numerical modeling techniques for FSI analyses described in chapter 4 were applied to the Middle Fork of the Feather River. The following sections describe the development of the CFD and CSM models.

Figure 26. Photo. Rock layout design for protection of pier 3.

Figure 27. Photo. Riprap installation near pier 3 (August 2012).
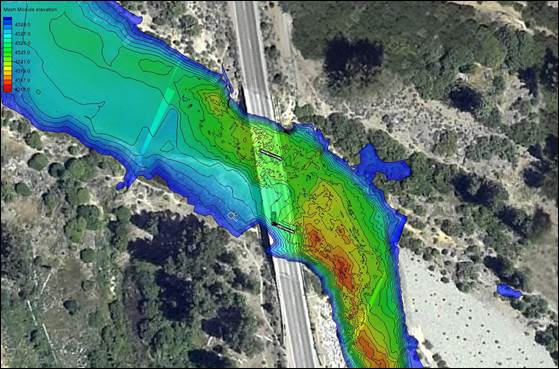
1 ft = 0.305 m
Figure 28. Photo. River bathymetry in 2013 after riprap installation.
The riverbed geometry model was constructed based on the 2011 bathymetric survey and GPS coordinates of the areas around the river. The bed surface in the CFD model was subdivided into river bed and grass surfaces with appropriate roughness coefficients for these boundaries as shown in figure 29. In addition, an area surrounding the pier was bounded with a box where a denser mesh could be used for more accurate results.
The point cloud bathymetry was numerically enhanced using Matlab and MeshLab.(12,13) The enhanced point cloud was triangulated to obtain a raw surface and imported into STAR-CCM+ as the initial geometry for the numerical model. Next, the bed geometry and the bridge geometry were transformed into a surface mesh. A volume mesh was generated with polyhedral cells. The covered domain was approximately 935 ft (285 m) long, 394 ft (120 m) wide, and 23 ft (7 m) high. As shown in figure 30, the model included pressure, velocity, and symmetry boundary types.
With this domain, large recirculation zones developed near the outlet creating problems enforcing pressure boundary conditions on the outlet. To remedy this situation, the domain was extended downstream another 984 ft (300 m). In the absence of detailed profile data for the river in that region, the extension was based on the most downstream cross-section of the surveyed domain and a longitudinal slope of 0.3 percent.
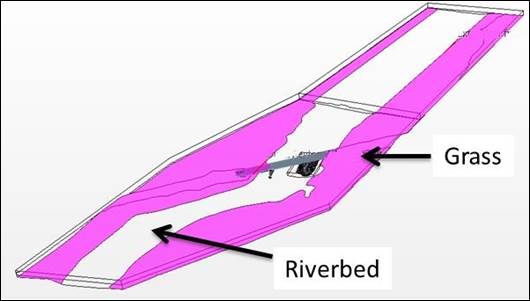
Figure 29. Schematic. CFD model surface characterization.
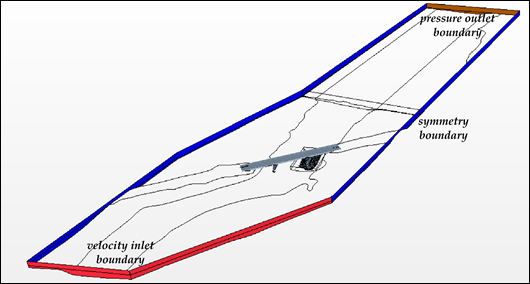
Figure 30. Graphic. CFD model boundaries.
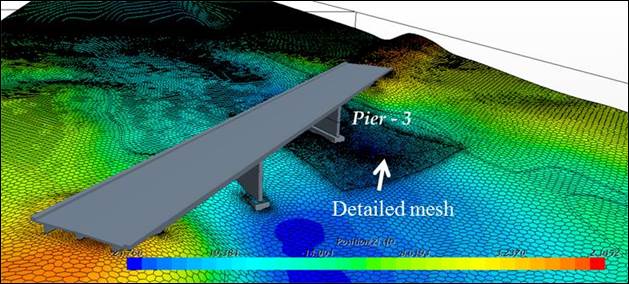
Figure 31 shows the surface mesh of the riverbed in the CFD model with the deepest point near pier 3. STAR-CCM+ software allows for fine gradation of the computational mesh in three dimensions. Very fine meshes can be specified in the areas of highest interest such as pier 3 in this application. Coarse meshes can be used in other areas to reduce computational cost. Local refinements can be further defined based on control volumes, surfaces, or edges.
The region in the vicinity of pier 3 was separated from the rest of the domain in the CFD model to facilitate data exchanges for the subsequent FSI analyses and to control the mesh size. Internal interfaces were placed on the boundaries of that subregion in contact with the outer global region. For the CFD modeling the extended global domain was used. However, for the FSI computations, only the subregion around pier 3 was used. Figure 32 shows the cross-section through the volume mesh in the global domain. The section marked with lighter (purple) color is the subregion used in the FSI modeling.
1 ft = 0.305 m
Figure 31. Graphic. Surface mesh of the riverbed in CFD model.

Figure 32. Graphic. Cross-section through the finite volume mesh used for the CFD model.
Figure 33 shows a close-up view of the mesh in the subregion. Mesh in that region is significantly denser than in the rest of the global model. The subregion contained approximately 2.2 million cells, while the global model covering a much larger volume included nearly 4.1 million cells.
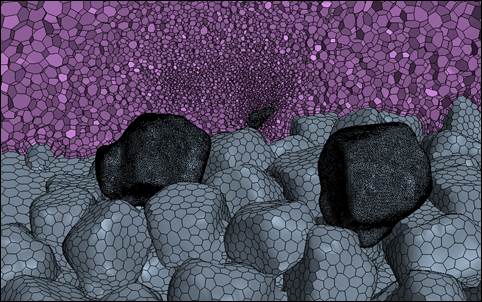
Figure 33. Graphic. Cross-section through the subregion used in the FSI computations.
As with the validation effort, the description of the riprap within the numerical models was a significant undertaking. These sections describe the development of these models from the design drawings with adjustments based on sonar soundings.
The riprap extent and surface slopes of the rock slope protection (RSP) were initially modeled after the design drawings shown in figure 34 and figure 35. Over 2,500 rocks were included in the CFD model. They were placed in the scour hole semi-manually, meaning smaller clusters of rocks were copied and changed slightly to introduce some variation in their shape and orientation. Once the desired layout was achieved, the STAR-CCM+ surface wrapper was used to smooth the geometry and create a continuous bed boundary. The final triangulated surface of the river bed is shown in figure 36. As noted in chapter 4, the rock geometry is simplified. The shape and orientation of the rocks are much less random than they are in reality and void spaces between the rocks may be larger allowing for more flow within the riprap voids.
In many riverine environments, as-built conditions may differ from design plans. To investigate as-built conditions, multiple sonar technologies were employed to characterize the bed at the pier. Initially, it was hoped that the sonar would help both in better defining the void spaces within the rock riprap installation, as well as for confirming the overall extent and surface shape of the riprap apron installation.
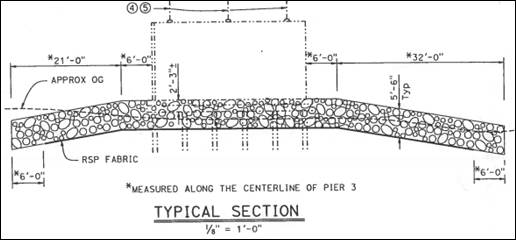
Figure 34. Drawing. Design drawing (typical section) of riprap around pier 3.
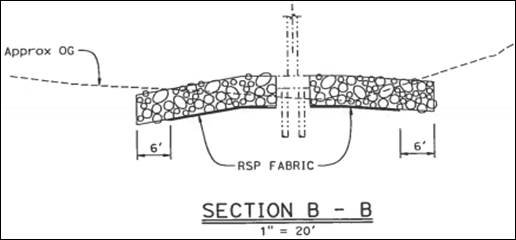
Figure 35. Drawing. Design drawing (section B-B) of riprap around pier 3.

Figure 36. Graphic. Geometry of the riprap used in the CFD model.
With respect to the void spaces, none of the sonar technologies were successful because they were not able to scan voids between the rocks; the void spaces were predominately out of the equipment view lines. Geometries created based on these limited scans would reduce flow between the rocks, effectively closing voids in the rock layers that do not show up in scans.
However, the sonar scans were successful in defining the overall riprap installation geometry. The scans identified the extent of the riprap and surface slopes on each side of the pier. The shape of a new embankment was also identifiable. Figure 37 shows a point cloud based on sonar scanning of the bed.
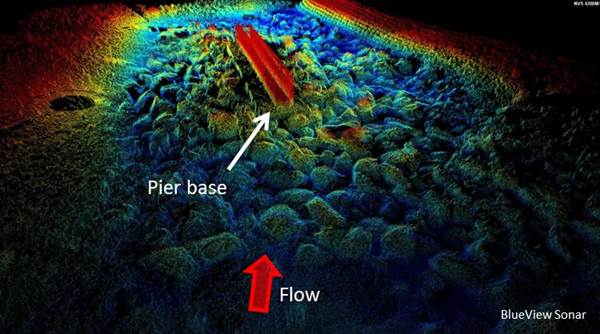
Figure 37. Image. Sonar image of pier 3 with installed riprap.
The scans reveal that the edges of the riprap installation differ from the design plans. An embankment not represented in the design drawings is also apparent in the sonar scans. Figure 38 shows the extent of the boundaries of the riprap installation based on the scan. These boundaries were compared with the extents included in the initial CFD model based on the design plans. The bed geometry and riprap boundaries in the model were adjusted with this new information, including the addition of the embankment on the right (looking downstream) of pier 3.
Figure 39 shows the updated model geometry of the riprap installation near pier 3. Most of the rocks are fixed. As described in chapter 4, movable rocks are placed in key locations for evaluating conditions under which they begin to move. The location of 40 movable rocks for this CFD model are also shown figure 39, in a darker shade.
According to the design documents, the average rock size for the riprap installation was specified to be 1 ton.(11) For typical rock density, 1-ton rocks are roughly equivalent to 3-ft (0.91-m) spheres or somewhat larger considering the irregular rock shapes. As a reference, the pier foundation is 6 ft (1.8 m) wide, meaning that the median rock size in the riprap installation should have dimensions slightly more than half of the pier footing width. In accordance with the specified riprap gradation, some rocks should be larger than 1 ton and some rocks may be smaller.
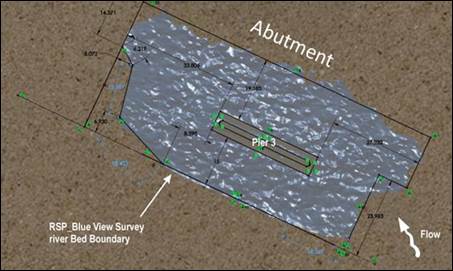
Figure 38. Graphic. The extent of the riprap derived from the sonar bed scan.
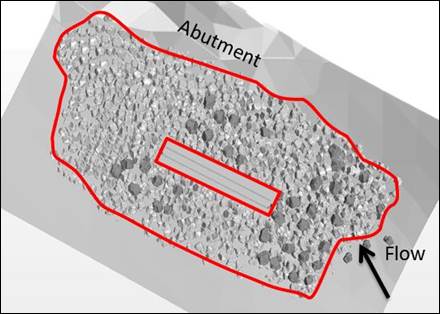
Figure 39. Graphic. Extent of riprap in the updated CFD model with movable rocks.
Inspection of the photo documentation record during the riprap installation (e.g., Figure 27) and the sonar results (e.g., Figure 37) suggests that few rocks at the site exceed 1 ton and many are smaller. Because of this observation, 10 movable rocks in each of 4 sizes (1 ton, 0.8 ton, 0.6 ton, and 0.4 ton) were included in the model.
The placement of movable rocks for this case study followed the same procedure described in chapter 4. After wrapping, the surface of the rocks was extracted and used in LS-DYNA as a rigid boundary. Approximate locations for the movable rocks were selected before the extraction. Subsequently, the movable rocks were dropped into position in the LS-DYNA simulation so that their final position is semi-random. The simulated drop assures that the rocks are in an equilibrium position before the FSI simulation starts. Figure 40 shows these positions and the rock sizes in the vicinity of pier 3. Some of the movable rocks protrude slightly above neighboring stationary rocks. Several of the smallest rocks (0.4 ton) rest at the front edge of the riprap installation and are entirely exposed to the flow.
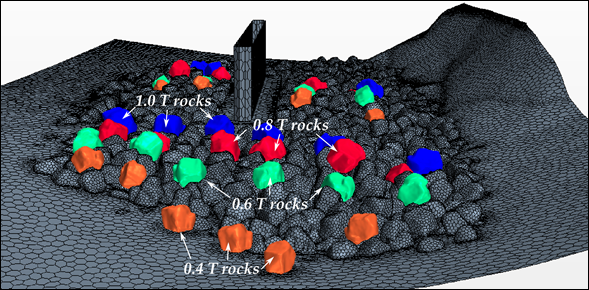
Figure 40. Graphic. Placement of movable rocks around the pier.
The three-dimensional (3D) CFD analyses were compared with the results of two-dimensional (2D) analyses performed by Caltrans.(11) The 100-year discharge of 30,100 ft3/s (852 m3/s) was used in both models. Table 4 summarizes the estimated depths upstream and downstream of the bridge. Both models show a significant elevation change between locations upstream and downstream of the bridge, but the 2D model depths are higher than the 3D model depths. Because of the higher upstream depths, the 2D model predicts that the bridge will be overtopped at the 100-year event, and the 3D model predicts the bridge will pressurize the flow under the bridge but will not overtop it.
Table 4. Comparison of 3D and 2D modeling results for the 100-year discharge.
| Parameter | 3D CFD | 2D |
|---|---|---|
| Depth downstream of bridge, ft (m) | 11.5 (3.5) | 14 (4.3) |
| Depth upstream of bridge, ft (m) | 18 (5.5) | 24 (7.3) |
| Bridge overtopping? | No | Yes |
Caltrans noted that for the 2D modeling the downstream boundary water surface elevation was estimated using a normal depth computation and a 0.3 percent slope, which may have resulted in an error of up to 2 ft (0.61 m).(11) This might explain some of the differences between the 3D and 2D models downstream of the bridge.
3D CFD calculations were performed with a time step of 0.1s. Quasi-steady state conditions were achieved in about 700 s of simulated time. It is not trivial to extract depth-averaged velocities (and other quantities) from 3D modeling to compare with the 2D model results. Therefore, the depth-averaged velocity was only calculated for a cross-section under the bridge as shown in figure 41. The velocities are in agreement only on the outer side of pier 3. However, for much of the cross-section, the velocity obtained in the 3D analysis was significantly higher averaging approximately 17.5 ft/s (5.3 m/s) compared with approximately 13.5 ft/s (4.1 m/s) for the 2D analysis. Higher velocities under the bridge estimated by the 3D model are consistent with the lower depths noted previously in table 4.
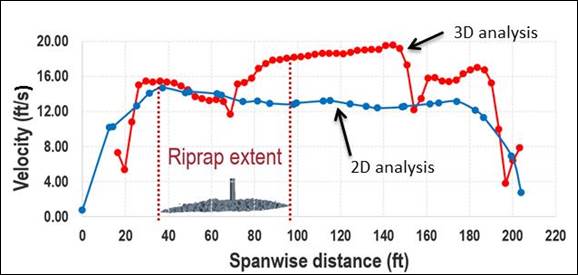
1 ft = 0.305 m; 1 ft/s = 0.305 m/
Figure 41. Graph. Depth-averaged velocity estimates under the bridge (looking upstream).
The results shown in figure 41 suggest that rock riprap designed using the 2D modeling results could be under-designed if the 3D results are a better representation of expected circumstances during the 100-year event. Furthermore, the occurrence of pressure flow for the 100-year event may contribute to under-designed rock riprap. The FSI modeling will be used to explore further the possibility that the rock might be under-designed.
The coupled FSI (CFD and CSM) models were implemented for the Middle Fork of the Feather River for the 100-year flood and two alternative scenarios. The results of the CFD and CSM analyses are described in this section.
From the initial CFD analyses, hydrodynamic forces on all movable rocks were extracted in a local coordinate system aligned with pier 3 and flow under the bridge. Figure 42 shows the location of the rocks with highest forces in each weight category from the CFD simulation of a 100-year flood event. For the 100-year event, the average inlet velocity was 11.1 ft/s (3.38 m/s).

Figure 42. Graphic. Location of the rocks with the highest forces in CFD analysis.
Table 5 summarizes the forces on the rocks, most of which are located to the west of the pier. Although these are the rocks experiencing the highest forces, other factors such as force angle and rock position influence which rocks may move first. The table also includes ratios of the hydrodynamic force on the rock to its weight. For 0.4-ton rocks weighing 800 lbf (3560 N) the ratios range from 0.77 to 0.87 while for the 1-ton rocks weighing 2000 lbf (8900 N) the ratios are lower and range from 0.62 to 0.65. As expected, it appears that the most vulnerable rocks are the smallest. Finally, the table includes information on rocks that move based on the FSI analysis discussed in the following section.
Two additional CFD analyses were conducted using incrementally higher inlet velocity and flow values. Table 5 also summarizes the resulting forces on the identified rocks and the ratio of the resultant forces to the rock weights. Holding the water surface elevation constant, the discharge and inlet velocities were increased by 10 percent (1.1 times the 100-year) and 20 percent (1.2 times the 100-year).
The objective of increasing the discharge and inlet velocity was to attempt to identify at what conditions the 1-ton rocks will begin to move. Small changes (10 and 20 percent increases) were used to avoid several potential problems. For example, an increase in discharge may make it difficult to compare one result to another because flow under the bridge might be different in these conditions if the entire river is modeled. In addition, overtopping of the bridge may occur for larger floods changing the velocity profile around the bridge.
Table 5. Forces on the critical rocks.
| Rock # | Rock Weight (lbf)** |
Force (lbf x 10-3)* | Ratio to Rock Weight** | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Q100 X Force |
Q100 Y Force |
Q100 Z Force |
Q100 Resultant |
1.1 Q100 Resultant |
1.2 Q100 Resultant |
Q100 | 1.1 Q100 |
1.2 Q100 |
||
| 5 | 2,000 | –196 | 551 | 1,146 | 1,285 | na | 1,488 | 0.64 | <0.67 | 0.74 |
| 6 | 2,000 | –13 | 378 | 1,236 | 1,292 | 1,467 | 1,593 | 0.65 | 0.73 | 0.80 |
| 8 | 2,000 | na | na | na | na | 1,431 | 1,445 | <0.62 | 0.72 | 0.72 |
| 9 | 2,000 | –294 | 326 | 1,157 | 1,238 | 1,346 | na | 0.62 | 0.67 | <0.72 |
| 13 | 1,600 | 20 | 247 | 843 | 879 | 980 | 969 | 0.55 | 0.61 | 0.61 |
| 17 | 1,600 | –90 | 382 | 831 | 919 | 975 | 1,016 | 0.57 | 0.61 | 0.63 |
| 19 | 1,600 | –34 | 562 | 1,202 | 1,328 | 1,613 | 1,728 | 0.83 | 1.01 | 1.08 |
| 25 | 1,200 | –213 | 297 | 775 | 856 | 998 | 1,045 | 0.71 | 0.83 | 0.87 |
| 26 | 1,200 | –85 | 243 | 775 | 818 | 960 | 1,031 | 0.68 | 0.80 | 0.86 |
| 27 | 1200 | na | na | na | na | na | na | <0.68 | <0.79 | <0.86 |
| 29 | 1,200 | –54 | 238 | 798 | 834 | 946 | 1,056 | 0.69 | 0.79 | 0.88 |
| 35 | 800 | 97 | 281 | 629 | 697 | 807 | 910 | 0.87 | 1.01 | 1.14 |
| 37 | 800 | na | na | na | na | na | na | <0.77 | <0.82 | <0.98 |
| 39 | 800 | 22 | 180 | 596 | 622 | 748 | 845 | 0.78 | 0.94 | 1.06 |
| 40 | 800 | 22 | 270 | 551 | 613 | 654 | 782 | 0.77 | 0.82 | 0.98 |
| *1 lbf = 4.45 N. **Shaded ratios indicate rocks that moved from their location based on the FSI analysis. |
||||||||||
Another potential problem is achieving realistic 3D CFD multi-phase simulation results in a reasonable amount of time. In VOF free surface simulations, specific conditions are set at a flow inlet, while fairly weak outlet boundary conditions are set. The outlet boundary conditions are normally either a specified pressure or a zero-gradient condition where the mass flow arriving at the outlet simply passes through with no velocity gradient, as though it is a fully developed flow field. A free surface or water elevation cannot be specified at an outlet. The problem with this is that for subcritical flows, the flow in the domain is controlled by the outlet conditions, most importantly the water elevation, that, while known, is not enforced by the software.
To overcome this challenge, the proper specification of the inlet water level and initial conditions in the entire domain is critical. A primary reason is that these flows are normally highly convective and information slowly propagates numerically from the outlet upstream to the inlet. An initial condition that is too far from the final solution may cause a sudden jump in water level at the inlet boundaries raising questions about the validity of the solution domain. Figure 43 illustrates this behavior for an analysis of the entire domain when the discharge was increased by 60 percent above the 100-year conditions.
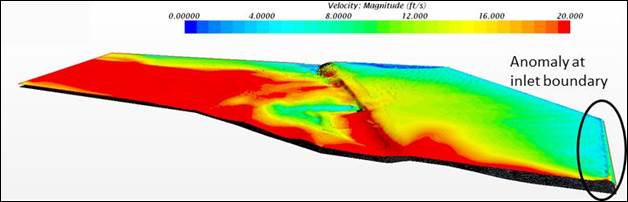
1 ft/s = 0.305 m/s
Figure 43. Graphic. Water surface (velocity overlain) for condition of 1.6 times the 100-year flood.
A second reason this challenge is difficult to overcome is that the CFD runs require several days on high performance computers to converge to a quasi-steady state. One solution is to take an iterative approach to adjust the water height at the inlet and the water height in the domain by changing the resistance of the flow in the domain (bed roughness, surface slope, and other solution parameters). However, for this approach to be practical, the size of the domain must be reduced. The reduced domain combined with the iterative approach provides more control over the inlet conditions and, ultimately, a more direct relationship between the inlet velocity and the velocities around the rock riprap installation.
As described previously, only the region closest to the pier with highest scour risk was used in the FSI modeling. The subdomain of interest together with velocity vectors for the 100-year flood on the outer boundaries are shown in figure 44. Velocities in the plane just above the riprap rocks are shown in figure 45. Average inlet velocity on the frontal face for that case was 11.1 ft/s (3.38 m/s).
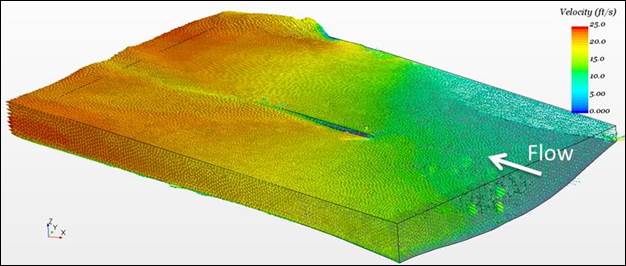
1 ft/s = 0.305 m/s
Figure 44. Graphic. Velocity vectors on the interface between the FSI subregion and the CFD domain.
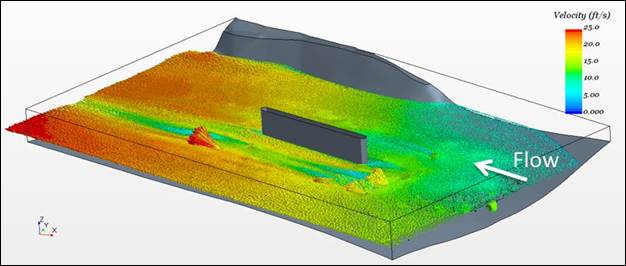
1 ft/s = 0.305 m/s
Figure 45. Graphic. Velocity vectors on the plane just above the rocks.
Figure 46 shows snapshots from the FSI simulation for the 100-year flood event. Of the 40 movable rocks in the simulation, only 2 moved from their placed location: rock 25 (0.6 ton) and rock 19 (0.8 ton). Another two—rock 5 (1 ton) and rock 37 (0.4 ton)—only moved locally. Table 5 provides the rock weight ratios and indicates which rocks moved during this simulation. Although all of the rock weight ratios were less than 1, the position and moment arms for the particular rocks contributed to their movement.
 |
| A. 0.5 seconds. |
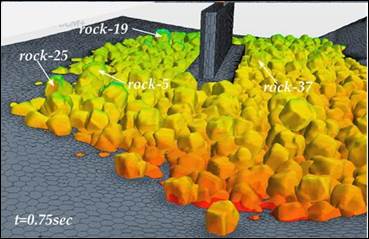 |
| B. 0.75 seconds. |
 |
| C. 1.0 seconds |
Figure 46. Graphics. FSI simulation for the 100-year discharge.
In the FSI simulation for 1.1 times the 100-year flood, movement of 6 out of the 40 movable rocks was detected. Five moved away from their initial positions within the simulated time: rock 5 (1 ton), rock 19 (0.8 ton), and rocks 25, 27, and 29 (0.6 ton). Rock 37 (0.4 ton) moved locally. Figure 47 shows several snapshots from that simulation. Table 5 provides the rock weight ratios and indicates which rocks moved during this simulation. This result also demonstrates that the rocks with the highest forces are not necessarily the ones that will move first because gravity and the reaction forces of surrounding rocks also play an important role in initiating and maintaining motion.
This FSI simulation was not conducted by slowly ramping up the velocity from the 100-year flood simulation as would be accomplished in physical modeling. Rather, a new simulation is started with new flow and boundary conditions. At current levels of computational power and software capabilities, a gradual ramping up of water velocity is too expensive. However, restarting at new conditions may introduce anomalies. For example, movable rock behavior at higher inlet velocities may appear to be unrealistic as instead of rolling over the neighboring rocks they are leaving their positions at steeper angles.
In the next case, the discharge and velocities at the inlet were multiplied by a factor of 1.2 times the 100-year simulation. At this faster flow, with more rocks moving, the mesh around the moving and colliding rocks experiences drastic deformations causing frequent simulation failure. Manual intervention was required to restart the analysis with modified mesh conditions to push the simulation forward. Because of these difficulties, this flow condition was only run for slightly more than 1.0 s of real time.
The FSI analysis indicates that eight rocks moved during the simulation; however, the simulation was not sufficiently long to conclude that other rocks would not have moved given more simulation time. Only a single 1-ton rock moved: rock 5. Also, only one 0.8-ton rock, rock 19, was set in motion. Four 0.6-ton rocks (25, 26, 27, and 29) moved and two 0.4-ton rocks (35 and 37) moved. Figure 48 shows the snapshot series for this flow condition. Table 5 provides the rock weight ratios and indicates which rocks moved during this simulation.
One objective for applying the FSI numerical modeling to the Middle Fork Feather River case study was to evaluate whether these tools could be effective for evaluation or design of riprap apron installations to protect bridge abutments and piers. The riprap installation at pier 3 of the bridge was intended to be stable for the 100-year flood event. The observations from the 100-year simulation were that only 2 rocks out of the 40 movable rocks moved from their original location and that neither of these rocks were the larger 1-ton rocks. When increasing the discharge and inlet velocity by 10 percent and 20 percent, the numbers of rocks moving were 5 and 8, respectively. These observations suggest that the installation will protect the pier foundation at the design discharge, but small increases in the discharge will likely result in riprap installation instabilities and, possibly, failure. Recalling from the validation process for the numerical modeling technique that rocks will move sooner in the numerical simulation compared with the physical situation reinforces the notion that the riprap is adequate for the 100-year flood.
 |
 |
| A. 0.0 seconds. | B. 0.5 seconds. |
 |
 |
| C. 1.0 seconds. | D. 1.5 seconds. |
Figure 47. Graphics. FSI simulation for 1.1 times the 100-year discharge.
 |
 |
| A. 0.0 seconds. | B. 0.3 seconds. |
 |
 |
| C. 0.7 seconds. | D. 1.0 seconds. |
Figure 48. Graphics. FSI simulation for 1.2 times the 100-year discharge.
Working against the conclusion that the riprap will protect the pier foundation is that the bed in the numerical model is fixed except for the 40 movable rocks. Because of this finding, the modeling may not identify fixed locations that might move causing an unraveling of the riprap integrity. In addition, the fixed bed does not allow for evaluation of the potential for undermining of the riprap resulting from an inadequately designed or installed filter layer.