U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-054 Date: October 2017 |
Publication Number: FHWA-HRT-17-054 Date: October 2017 |
This appendix provides details of the coupling and verification for the FSI solutions used in this study. This information is taken from Bojanowski et al.(10) Readers interested in more information should consult that reference.
While there has been an interest in solving FSI problems for decades, large computer clusters capable of solving them for full scale systems have only become widely available to engineers in the past decade. In addition, moving and morphing mesh capabilities in CFD software needed to solve FSI problems have only recently matured to the point at which they can be reliably used. This maturity was necessary before the coupling of CFD and CSM software could be expected to be successful.
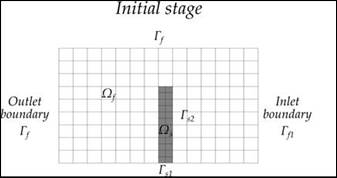
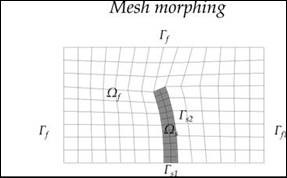
Figure 49 presents a schematic of a discretized computational domain with fluid occupying space (Ωf) and solid body occupying space (Ωs). The symbol Γ represents boundary conditions with the subscripts s and f referencing the solid and fluid boundaries, respectively. The numerical subscripts on the boundary conditions represent different types of boundary conditions. Application of the RANS equations for Newtonian incompressible fluids with a k-epsilon turbulence model to solve for the flow field and pressure distribution on the boundaries is a standard computational approach.
 |
 |
| A. Initial. | B. Intermediate. |
Figure 49. Schematics. Stages of FSI mesh morphing.
In most classic CFD problems, the boundaries are fixed during the analysis, and the computational mesh does not change. Notable exceptions are turbo machinery and in-cylinder combustion simulation in which special techniques were developed to handle the moving boundaries. In FSI problems, the fluid boundaries may be part of a structure that will move or deform in response to surface and body forces that are determined as part of the solution of the problem as shown in figure 50. In this case, fixed rocks in the riprap layers represent solid boundary conditions (Γs1) while the movable rocks are represented as solid body occupying space (Ωs). As the boundary motion is calculated, the computational mesh in the fluid domain has to be updated either by a morphing procedure or by a complete domain remesh process.
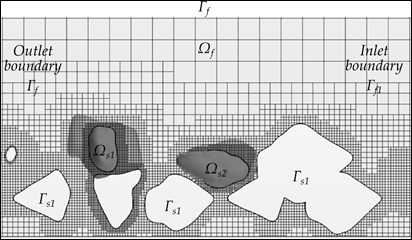
Figure 50. Sketch. Definition of the domains for FSI analysis of riprap stability.
The CFD solution of the fluid flow equations yields the detailed distribution of fluid stress on the solid surfaces. This stress distribution is passed to the CSM software to solve for the response of the solid bodies, and that solution yields the displacement rate (velocity) distribution of the solid surfaces. In general, the surface velocity distribution may include both deformation and rigid body motion. In the analysis of riprap rock motion, it includes only rigid body motion. The motion computed by the CSM software is passed back to the CFD software as a boundary condition that is a function of time.
In general, there are two groups of coupling solutions for FSI problems: monolithic and partitioned.(40) The monolithic approach involves solving the coupled set of equations for the fluid and structural domain as a single problem. Although this approach may seem the most desirable, it can be more difficult to adjust solver parameters to obtain a converged solution than with the partitioned approach. The use of robust CFD and CSM software from vendors who specialize in those areas naturally leads to using a partitioned approach in which the equations are solved iteratively one domain at a time and coupling conditions are set via file-based data exchange from the solution of the other domain.
Depending on the influence of interface boundary condition changes from either the solid or fluid domain on the other domain one-way or two-way coupling may be needed to solve the problem. If, for example, displacements of the solid resulting from fluid forces are small enough so that they do not substantially influence the fluid flow, then one way coupling from the fluid domain to the solid domain can be used. In this case, the pressure distribution on the solid is not affected much by its motion, and therefore flow equations need to be solved only once to obtain the load from the flow on the solid. However, for FSI analysis of riprap the motion of a rock results in an evolving position and orientation that substantially changes the pressure distribution over the surface of the rock, requiring two-way coupling.
Two-way coupling can be either weak or strong. In a weak coupling, as shown in figure 51, the solution in the fluid region at time step (n) including the pressure and shear stress distribution, is found on the movable riprap wall boundaries at the start of time step obtained from the structural solver from the previous step (n – 1). This distribution is passed subsequently to the structural solver, which yields a solution giving the solid boundary displacement and velocity that is passed to the CFD solver for use in time step (n + 1). The structural solver may require a smaller time step (δts) than the fluid solver time step (δtf) if contact, such as a rock colliding with surrounding rocks on the bed, is modeled. The number of structural solver time steps within each fluid solver time steps is represented by a multiplier (m). The coupling time step represents the frequency of data exchange between the two solvers. The coupling time step must be an integer multiplier of both solver time steps. In figure 51, the coupling time step is equal to the fluid solver time step. The number of steps and length of time steps for each solver is determined by the complexity of the physics modeled in each solver.
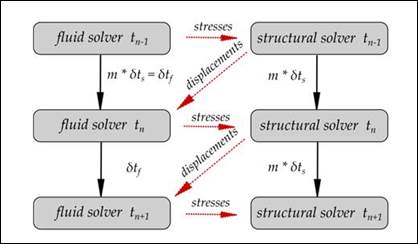
Figure 51. Flowchart. Weak FSI coupling scheme.
Figure 52 presents a schematic of a strong coupling procedure. In this scheme, the two problems are also numerically decoupled. However, within each time step (n) the CFD and CSM solvers exchange interface conditions computed by the separate solvers during the iteration (im) to converge during the time step. An updated location of the structure boundary in the structural step is fed to the CFD model and a new pressure field is found. Instead of progressing to the next step, the updated pressures are used again to find a different state of the structure within the same time step.
The weak coupling for this study involved two separate solvers: STAR-CCM+ performing CFD calculations and LS-DYNA performing structural analysis.(3,4,41) Both of these software packages have limited FSI capabilities. However, LS-DYNA does not yet have sufficiently robust fluid flow solvers and the wide range of flow physics models available in STAR-CCM+. Conversely, STAR-CCM+ recently implemented the contact capabilities for rigid bodies, but the algorithm is not able to efficiently model multiple rocks colliding with each other. A variety of models for particle-particle and particle-wall interactions exist in STAR-CCM+, but these are sub-grid models of particles not represented in the mesh. For the purpose of analyzing the onset of motion of riprap rocks, modeling the effects of contact forces between objects represented in the mesh is an essential feature.
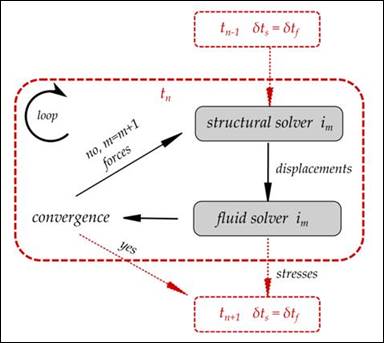
Figure 52. Flowchart. Strong FSI coupling scheme.
Therefore, the analysis is split into two different problems. STAR-CCM+ calculates the flow field and the pressure distribution on rocks. LS-DYNA calculates the motion of rocks resulting from the stresses exerted by the fluid on the rock surface and the effects of contact forces. A new position of a rock after the coupling step is subsequently imported into STAR-CCM+ as a basis for calculation at the next time step. Because the rocks are treated as rigid bodies, a weak coupling procedure is sufficient to obtain first order accuracy in the solution of rock motion. The small time step required in LS-DYNA to model body interactions and in STAR-CCM+ to maintain stable mesh morphing was assumed to be sufficient to compute the onset of rock motion and the trajectory.
Figure 53 presents the workflow of the procedure to analyze incipient motion of riprap for a given arrangement and flow velocity. The workflow is executed by a combination of tools including manual execution, macros (in Java), ad a control program (in Python). The control program initiates execution of needed components of LS-DYNA and STAR-CCM+, including the solvers and meshing software. It also translates output files into a format recognized by both software packages.
The analysis procedure begins with initialization runs in both solvers. The LS-DYNA run provides the initial position of the rocks under gravity loading. This position is used as a basis for CFD domain geometry. The CFD model is run until quasi steady state conditions are achieved with all rocks stationary. Execution of the CFD part is quite complex and requires an internal Java macro to run within STAR-CCM+ to import rock displacements and map them from the CSM mesh to the CFD mesh and vice versa. It is almost always the case that the resolution between the fluid and structural grids is different, especially when two separate solvers are handling the fluid and solid domains. STAR-CCM+ provides accurate data mappers for non-conforming meshes.(3) This mapping is performed at each time step as the underlying mesh deforms. The displacements of the body are distributed throughout the morphed fluid domain to maintain cell quality. No cells are added or removed in the morphing process and their neighbor relationships are preserved, thus the mesh topology remains constant. The Arbitrary Lagrangian-Eulerian (ALE) algorithm is invoked to solve transport equations resulting from the moving underlying mesh.(3,41) Furthermore, this algorithm allows for retaining the exact shape of the interface between the solid and the fluid.
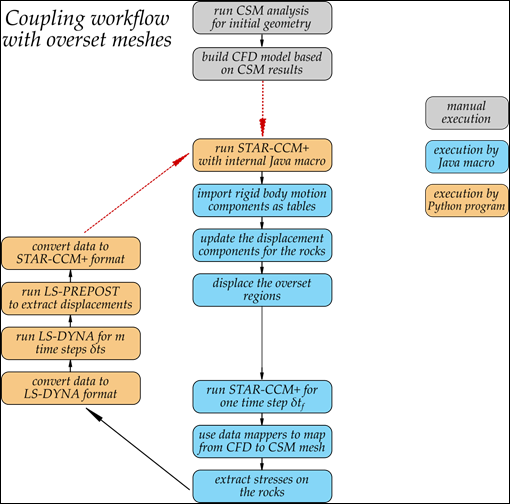
Figure 53. Flowchart. Implementation of coupling workflow between STAR-CCM+ and LS-DYNA.
Most of the effort in the FSI coupling was investing in resolving moving and morphing mesh problems that arise when rock motion collapses the space between a rock and another solid surface and problems that arose in the mapping and data exchange between the CFD and CSM software. The resolution of these problems yields coupling software for data mapping, data exchange, and automated mesh morphing failure recovery that make it possible to carry out the analysis.
The mesh morpher uses a sophisticated algorithm that yields a high-quality mesh in the whole computational domain based on the initial mesh and the displacement of the boundaries. However, in cases during which the displacement of a rock becomes large or it comes in contact with a solid boundary, the cells may become too distorted and of such poor quality that the solver either diverges or encounters a floating point exception condition. In such cases the Java macro executes a computationally demanding remeshing of the whole domain. The time step of calculations is selected such that full domain remeshing is avoided in the initial steps. The functioning of automated procedures is demonstrated in computation of water flow at increasing velocities until rock motion into the downstream occurs.
The initial proof-of-concept used the geometries of four rocks in which only the top rock was free to move as presented in figure 54-A. The coupling procedure worked very well in the first several steps. The volume mesh in STAR-CCM+ was morphed each time a new position of the moving rock was imported. However, after several remeshing cycles the shape of the moving rock started to degenerate. During the remeshing stage a standard approach was to extract the current surface mesh in STAR-CCM+ and build the new volume mesh based on that extracted surface. It was discovered that the interpolation and discretization process introduced an error forcing the fluid volume to expand slightly beyond the boundary on irregular surfaces. As a consequence, the moving rock shrinks in size through repeated remeshing operation as the water moves the movable rock off of the others as shown in the sequence of figure 54.
It was concluded that the only workaround for this problem was to preserve the irregular rock shape by wrapping the rock mesh with a large number of curves, called feature curves. The meshing algorithms treat features differently from general vertices defining the position of a surface. For feature curves, the meshing algorithm tries to maintain the geometry of the curve within a much smaller tolerance than that of the surface in general. Figure 55 shows the finely meshed surface of a rock with dense feature curves.
Using commercial software rather than research software has many advantages. The primary advantage it the large industrial user base engaged in using commercial software successfully to solve problems. Consequently, computed results are reliable within the accuracy of the physics models used. Vendors responding to the needs of industry also implement a wide array of physics models, methods to solve a variety of moving mesh problems, and advanced solver algorithms. They normally provide a means for users to add new physics models in the form of user defined subroutines or functions. As such, they provide an excellent foundation for building models to solve new problems, or analyze classic problems using advanced analysis techniques.
One disadvantage of using commercial software is that the users do not normally have direct access to the source code and therefore cannot make even minor modifications that might be needed for a new model development outside of the means provided by the vendor. That confines the user to the set of models and tools provided by the vendor. The current implementation of coupling between STAR-CCM+ and LS-DYNA allows for capturing the main effects of rock motion, however, when domain remeshing occurs, some of the information about the motion of a rock through time is lost. In addition, the grid fluxes are not included in the momentum equations immediately after remeshing. As a result, the reduction in drag from the acceleration of a rock is not fully considered and rock motion with large displacements will occur at a slightly lower velocity difference between the rock and mean flow. The error in this case is conservative in the sense that it would lead to slightly oversizing the riprap for a particular application. At the onset of motion the displacements and velocities of the rocks are so small that this effect should be small.
 |
| A. Initial. |
 |
| B. Intermediate. |
 |
| C. Final. |
Figure 54. Schematics. Stages in the coupled simulation for water induced rock motion.
The fact that only a weak coupling was implemented has its advantages and disadvantages. The obvious advantage is the computational time. Because within each coupling time step there are no inner iterations and only one exchange of the data is performed per time step, this type of coupling is sometimes called explicit. For flexible structures vibrating in the flow frequently this approach diverges quickly and a strong coupling (implicit) is needed to stabilize the solution. For rigid rocks this behavior was not observed and weak coupling was assumed to be sufficient for this work.
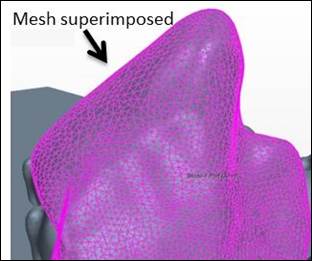
Figure 55. Graphic. Rock representation with feature curves created on all edges of the mesh.
While the coupling procedure was under the development for this study, Siemens introduced a new approach to modeling the motion of objects within the computational domain using so-called overset meshes. This approach does not rely on morphing and remeshing of the domain. Instead, it encapsulates a moving object in its own small domain that shares the space with the background global domain. During the computation, the background mesh is carved out in the place where the local mesh is and new internal boundaries are built between the local and the global mesh. The results are interpolated from the global mesh to the local mesh on these boundaries and the local mesh is treated as a part of the global model. Potentially, this method is offers several advantages for modeling FSI problems: (1) reduction of overall run time because there is no need for time consuming remeshing, (2) improvement of stability because only one mesh is used throughout the simulation, and (3) improved accuracy.
In the new procedure, an overlap of the subregions and the background mesh is computed at each time step and an interpolation interface between these regions is redefined accordingly. Active and inactive cells are found in the rock and background regions at the beginning of each time step. In addition, motion of the overset regions is defined as rigid body motion based on the calculations performed in LS-DYNA (or internal finite element solver of STAR-CCM+). For overset regions, rigid body motion is specified by using just six components per time step. Previously, a displacement vector for each vertex on the rock boundary was defined separately.
The overset mesh procedure is more computationally efficient than the procedure based on mesh morphing and remeshing. The coupling iterations were executed faster than the previously described implementation. However, while the procedure with overset meshes solves some problems, it introduces new ones. When tracing the forces acting on a single rock during its motion, it was noticed that this approach generates unrealistically high forces on the rocks that do not converge to reasonable values within one time step.
The overset mesh method has been under heavy development and improvements are expected in future releases of STAR-CCM+. In addition, recent implementations of the overset mesh approach also allow for contact between moving objects and wall boundaries. Initial tests indicated that the implementation of contact algorithms in STAR-CCM+ is not robust yet. However, with the short development cycles of STAR-CCM+ it may be possible to simulate the entire FSI riprap problem in STAR-CCM+ only once these components and models work well together with the finite element solver internal to STAR-CCM+ in the near future.
At the time of this study, the procedure with morphing and remeshing seems to be conceptually most reliable and it appears to generate the most stable results. In addition, the results from the procedure and are conservative. Therefore, it was used to perform all the calculations reported in this study.
The coupling procedures described in this report were developed primarily for analyzing incipient motion of rocks used in riprap around piers or abutments to prevent scour of the riverbed at these structures. Prior to this more complex case, a simple, flatbed geometry case with only riprap rocks was used as a development case until all of coupling problems were resolved. This simple case also allowed for comparison with Laursen’s and Neill’s equations for critical velocities.(42)
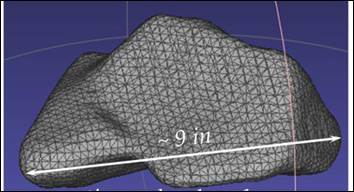
Model development started by processing the surface point cloud data from a 3D laser scan of a rock to be used in the demonstration. MeshLab software was used to generate a surface triangulation of the rock as shown in figure 56.(12) The initial shape was subsequently modified by simple geometrical operations to create a set of rocks with similar shapes to populate the domain for testing.
1 inch = 25.4 mm
Figure 56. Graphic. Surface triangulated representation of a rock.
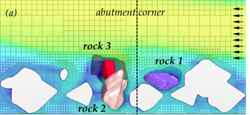
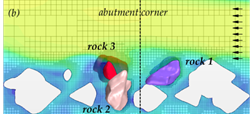
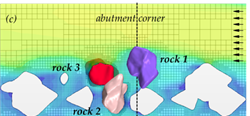
Two layouts were considered for these simple tests. Layout 1 is placement of a riprap layer in a depressed section so that the top of the layer is flush with the surrounding surface. Profile and plan views are shown in figure 57-A and figure 57-B respectively. Layout 2 includes an abutment along with a similar riprap layout as shown in figure 57-C. All of the rocks in the figure are stationary except for the three individually labeled as rock 1, rock 2, and rock 3. The movable rocks can interact with other boundaries and among themselves through contact algorithms enabled in LS-DYNA.
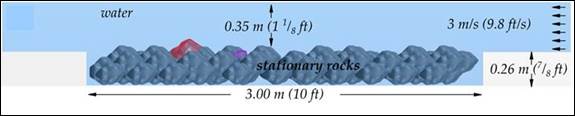 |
| A. Layout 1, profile view. |
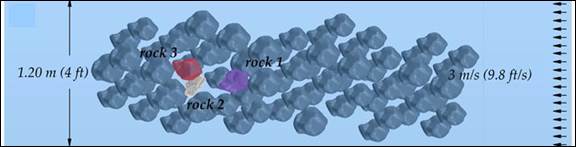 |
| B. Layout 1, plan view. |
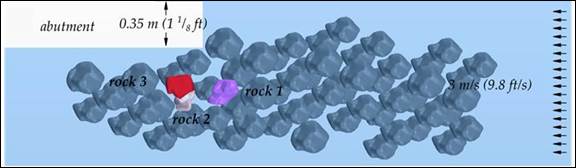 |
| C. Layout 2, plan view. |
Figure 57. Graphics. Test CFD models.
Rock shapes and layout influence when they are picked up and moved by the passing flow. Placing the rocks at different locations ensures that each of them will have a different critical velocity determined by the detailed geometry and flow field computed in the simulation. Rock 1 and rock 2 are the same shape as the originally scanned rock in figure 56. Rock 1 is placed flush among the other rocks in the bed. Rock 2 is placed quite deep under the top surface. Rock 3 is bigger and more round than the other two and is protruding slightly above the bed.
A CFD domain was built with dimensions 16.4 ft long, 3.94 ft wide, and 2.1 ft high (5.0 m long, 1.2 m wide, and 0.65 m high) in the recessed area containing the rocks of the riprap layer. The height of the water from the top to the riprap bed top surface was approximately 1.15 ft (0.35 m). The size of the domain was designed to be small to conserve computational resources and provide fast turnaround times during development and testing of the coupling procedures. A single phase rigid lid model of the channel flow was used to keep the model simple.
The initial water velocity in the domain and the velocity at the inlet was a variable parameter that was manually set for each test. The sides of the domain were set as symmetric planes. The downstream end of the model was set as an outflow boundary. In layout 2 (with the abutment), the abutment was set as a wall boundary and the approach flow boundary on the abutment side of the domain was also set as wall boundary. The opposite side was set as a symmetry plane.
The domain was meshed using hexahedral cells with varying cell size from 0.16 inches (0.004 m) around the rocks up to 2.4 inches (0.06 m) away from the rocks and other boundaries. The total count of cells in the model varied between 1.5 million up to 2.0 million cells depending on the layout (without or with abutment) and the evolving position of rocks during the simulation. A k-epsilon turbulence model with RANS equations was used to solve for the flow field. An implicit unsteady solver with time step of 0.01s was used in the flow solver. The same time step was also used as the coupling time step, that is, the rate at which data between the CFD and CSM solvers was exchanged.
In LS-DYNA, the rocks were modeled as rigid bodies with a density similar to granite: 0.091T/ft3 (2.9 t/m3). The mass of rocks 1 and 2 were each 4.1 kg (9.0 lb) and the mass of rock 3 was 7.1 kg (15.6 lb).
Three contact definitions were incorporated in the model: (1) among the moving rocks, (2) between the moving rocks and the stationary rocks, and (3) between the moving rocks and the boundaries. It is sometimes advantageous in LS-DYNA to wrap solid bodies with null, massless shell elements to have more flexibility in defining the contact properties. One of advantages of such an approach is the use of a non-zero thickness layer around the rocks that prevents them from coming into a full contact in STAR-CCM+. Using this method prevents morphed cells in a near contact zone from being squeezed to near zero volume and causing flow acceleration to unrealistically high velocities in crevices.
The time step of calculations in the LS-DYNA explicit solver was set to 4.5x10–6 s. Use of the explicit solver and a small time step was needed to stabilize the contact forces between rocks colliding with other rocks or wall boundaries. A time step that is too large can cause excessive contact forces and abnormal behavior of the rocks. Once the STAR-CCM+ and LS-DYNA models were initialized, the coupling between them was activated.
The velocities at which motion for the movable rocks was initiated were compared with estimated critical velocities as a partial evaluation of the FSI simulations. Approximate values for critical velocity of the modeled rocks can be found by using the Neill and Laursen equations, both of which are applicable to the rock sizes being modeled.(42) Laursen’s equation is given by the equation in figure 58.
![]()
Figure 58. Equation. Laursen’s equation for critical velocity.
Where:
VCL = Critical velocity estimated from Laursen’s equation (ft/s (m/s)).
KU = Unit conversion constant (11.7 for US customary units (6.19 for SI units)).
y = Flow depth (ft (m)).
D50 = Median particle size (ft (m)).
For median particle sizes above 0.1 ft (0.03 m), Neill’s equation for critical velocity is defined in figure 59.
![]()
Figure 59. Equation. Neill’s equation for critical velocity.
Where:
VCN = Critical velocity estimated from Neill’s equation (ft/s (m/s)).
KU = Unit conversion constant (1 for US customary units (0.55217 for SI units)).
Taking y = 1.15 ft (0.35 m) and D50 = 0.79 ft (0.24 m), the critical velocities are 10.8 ft/s (3.31m/s) and 10.6 ft/s (3.23 m/s) according to Neill and Laursen, respectively.
The computer simulations were run with inlet velocities of 6.6, 8.2, and 9.8 ft/s (2.0, 2.5, and 3.0m/s) for each of the two layouts. The simulations were observed for motion of the movable rocks. For both layouts (without and with the abutment) motion was not observed at an inlet velocity of 6.6 ft/s (2.0 m/s). Because this velocity is less than the estimated critical velocity from both Neill and Laursen, motion was not expected. At a velocity of 8.2 ft/s (2.5 m/s) local motion (rocking in place) of rock 3 was noticeable, but it did not move from its position. Recall that rock 3 is the largest of the three movable rocks, but also is the most exposed to the flow field.
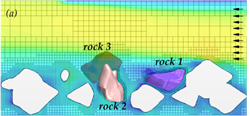
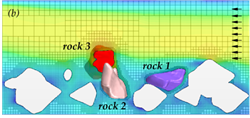
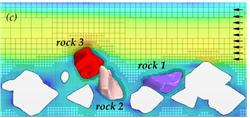
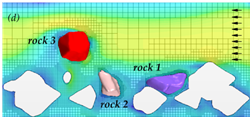
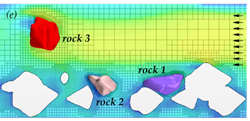
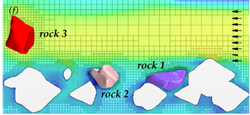
At a velocity of 9.8 ft/s (3.0 m/s) for layout 1 (without abutment), rock 3 was lifted out of position and moved downstream as shown in the time series of graphics shown in figure 60. (Several of the stationary rocks were removed from the view to more easily see the position of the moving rocks.) The figure also displays a semi-transparent cross-section through the domain showing the velocity distribution in the flow field. In addition to the displacement of rock 3, rock 2 exhibited local motion, but did not leave its position.
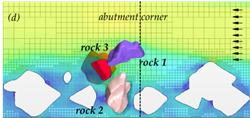
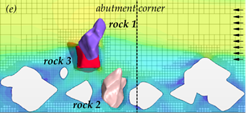
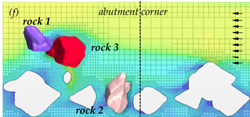
Similarly, at a velocity of 9.8 ft/s (3.0 m/s) for layout 2 (with abutment), rocks 1 and 3 were lifted out of position and moved downstream as shown in the time series in figure 61. The presence of the abutment altered the flow field and altered the movable rock responses, as a result.
Simulated rock movement at 9.8 ft/s (3.0 m/s), in both layouts, occurred at a velocity less than 10 percent lower than the values anticipated by the Laursen and Neill equations. It had been noted previously that the use of the closed lid approximation would result in rock motion at somewhat lower velocities than would be observed in the physical world. Therefore, this test was considered to be a successful demonstration of the coupled FSI modeling developed for this study.
 |
 |
| A. Time equals a. | B. Time equals b. |
 |
 |
| C. Time equals c. | D. Time equals d. |
 |
 |
| E. Time equals e. | F. Time equals f. |
|
1 ft/s = 0.305 m/s |
|
Figure 60. Graphics. Time series for layout 1 at an inlet velocity of 9.8 ft/s (3.0 m/s).
 |
 |
| A. Time equals a. | B. Time equals b. |
 |
 |
| C. Time equals c. | D. Time equals d. |
 |
 |
| E. Time equals e. | F. Time equals f. |
1 ft/s = 0.305 m/s |
|
Figure 61. Graphics. Time series for layout 2 at an inlet velocity of 9.8 ft/s (3.0 m/s).
The STAR-CCM+ manual contains an FSI example solved in a coupled system of STAR-CCM+ and Abaqus. STAR-CCM+ has a built-in interface for this coupling that allows for strong and weak coupling of the codes. For verification purposes this same FSI example problem was also solved using coupling procedure developed for this study.
The problem is to model the vibrations of a flexible rectangular plate standing in a 32.8 ft/s (10m/s) cross wind as shown in figure 62. The plate is constrained at its bottom edge perpendicular to the wind flow. The plate is 0.33 ft high, 0.26 ft wide, and 0.0082 ft thick (0.1 m high, 0.08 m wide, and 0.0025 m thick). The flexible plate was modeled with the following elastic properties and material constants: (1) Young’s modulus of 5570 lbf/in2 (38.4 MPa), (2) Poisson’s ratio of 0.3, and (3) density of 255 lb/ft3 (4096 kg/m3). The model domain has a width, height, and length of 0.95 ft, 0.66 ft, and 2.95 ft (0.29 m, 0.2 m, and 0.9 m), respectively, with the plate located 1.3 ft (0.4 m) from the model inlet.
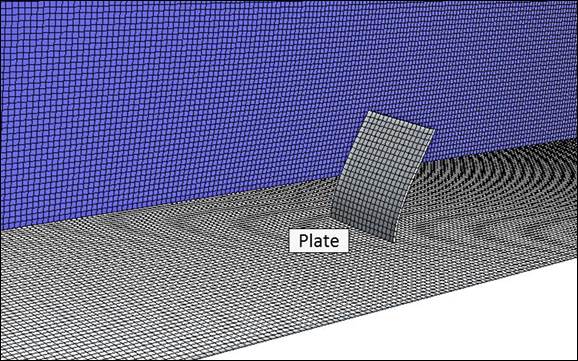
Figure 62. Schematic. CFD domain and grid for analysis of flexible plate protruding into the flow setup for FSI analysis coupling with LS-DYNA.
Figure 63 shows the mesh in proximity to the deformed plate for the coupling with Abaqus and LS-DYNA. The domain was modeled in Abaqus with polyhedral cells and in LS-DYNA with hexahedral cells. The overall model was built with around 300,000 cells. The configuration shown is captured at the state of the largest deflection of the plate. Figure 64 shows the displacement history of the two top corners of the plate. The maximum amplitude and the period of vibrations were predicted to be about the same magnitude by both coupling mechanisms. The local oscillations of corners of the plate behaved slightly differently. This was attributed to differences in coupling handling and different theoretical formulation of the solid elements. The comparison between the two modeling approaches showed general agreement.
 |
 |
| A. Abaqus coupling. | B. LS-DYNA coupling. |
Figure 63. Schematics. Morphed mesh at maximum plate deflection.
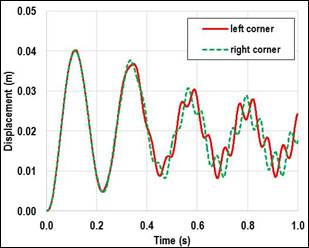 |
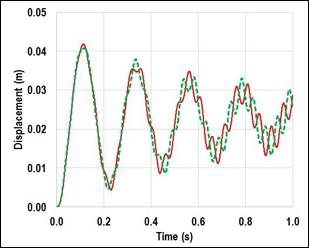 |
| 1 ft = 0.305 m A. LS-DYNA-STAR-CCM+ coupling. |
1 ft = 0.305 m B. Abaqus – STAR-CCM+ coupling. |
Figure 64. Graphs. Plate deflection.