U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-17-054 Date: October 2017 |
Publication Number: FHWA-HRT-17-054 Date: October 2017 |
Numerical modeling to evaluate the incipient motion and movement of rock riprap was conducted at the Transportation Research and Analysis Computing Center (TRACC) at Argonne National Laboratory. Most of this chapter describing the development and testing of the modeling tools is taken from Bojanowski et al.(10) The interested reader will find more detail in that reference, and in appendix B.
From a computational mechanics point of view, the analysis of riprap stability can be considered an FSI problem. FSI problems involve solving for the fluid flow forces on a solid surface, the response of that solid to the load, and subsequently, the change of the flow conditions caused by displacement of the solid. CFD software is used for solving fluid flows and CSM software is used for solving the deformations and stresses in solid bodies.
Historically, these software tools developed independently. In recent years, a number of CFD and CSM software vendors have been developing the capabilities needed to solve FSI problems. In many cases, these vendors are recognized leaders in the field of either CFD or CSM but not both. Integrated FSI software, if available, is not yet mature nor well tested by industry. Until industry-proven FSI solvers are available, coupling highly robust and reliable CFD and CSM software through the development of data exchange and concurrent control coupling procedures appears to be the best approach for solving complex engineering FSI problems.
For this project, FHWA engaged the services of the TRACC for FSI modeling. TRACC has licenses, a user base, and in-house expertise in the use of the software for the STAR-CCM+ CFD software and the LS-DYNA CSM software. For this project, TRACC developed coupling procedures between these software packages to support detailed analysis of riprap stability.
NCHRP report 568 lists four major failure Modes for riprap revetments: (1) slope failure resulting in a slide, (2) riprap particle erosion, (3) erosion beneath the riprap armoring layer, and (4) erosion of the toe or key of the revetment leading to a slide.(2) The methods described in this chapter can be applied to analyze failure Modes (1), (2), and (4). However, a model capable of describing scour beneath riprap revetment would be required to analyze failure Mode (3).
Modeling rock motion must overcome several challenges. One is sufficient characterization of the complex geometry of the bed in the vicinity of a pier or abutment. A riprap apron may include hundreds of rocks placed in a semi-organized manner in several layers. Representing each rock in the model is currently infeasible. However, sufficient engineering accuracy may be obtained with a reasonable approximation of the armored bed geometry.
A second problem pertains to the extent of the domain to be modeled with CFD for proper representation of flood conditions. The upstream boundary of the computational domain needs to be a sufficient distance away from the zone of interest so that the velocity profile can develop by the time the flow reaches the area of the bridge. Variations in river bed bathymetry constantly perturb the velocity profile. In most cases, placing the upstream boundary at least ten river hydraulic diameters upstream is sufficient. Similarly, the downstream outlet boundary must be sufficiently removed from flow obstructions so that recirculation zones created by flow obstructions, such as bridge piers, do not cross the outflow boundary. If the downstream boundary is too close to an obstruction, a recirculation zone may pull fluid into the domain through the outlet boundary violating the boundary conditions and the computation normally diverges. The outlet boundary should also be sufficiently removed from the zone of interest. Placing the outflow boundary at least ten river hydraulic diameters downstream of the last obstruction is usually sufficient.
STAR-CCM+ can address both issues because it can accommodate millions of computational cells. However, physically obtaining detailed bathymetry of a river bed is difficult and expensive.
Proper handling of the changes in the geometry within the CFD model is a third issue. STAR-CCM+ is capable of solving flow problems in domains containing solid objects with complex, irregular geometry in relative motion along arbitrary paths through the fluid domain using mesh motion and mesh morphing techniques. These capabilities allow for the deformation of the computational mesh to accommodate moving boundaries. During this process, new cells are not created and the solution is mapped from the old mesh to the new deformed mesh. However, large displacements of rocks as well as collisions between the rocks may cause the stretched cells to lose sufficient cell quality for an accurate solution of the governing equations or the algorithm may collapse cells causing negative volume cell termination of the computation. Automatic interaction between morphing and remeshing of the domain when cell quality becomes too poor is not available in STAR-CCM+. While STAR-CCM+ can model some rigid body interactions with a fluid in motion and has some capability to describe collisions between solid bodies, modeling of collisions is not yet sufficiently robust to describe the onset of motion for rocks.
LS-DYNA software is a general purpose finite element program capable of simulating highly non-linear problems in structural mechanics including changing boundary conditions (such as contact forces between rocks that change over time), large displacements, large deformations, and non-linear material property relations. Recent updates to LS-DYNA included the release of a new CFD solver that is coupled to its structural solver. LS-DYNA includes morphing and automatic remeshing interaction; however, the coupled CFD solver is not capable of handling the large domains required for stream flood modeling. In addition, the meshing capabilities are limited to tetrahedral elements and the physics models in LS-DYNA are limited compared with STAR-CCM+.
These issues with LS-DYNA or STAR-CCM+ lead to the conclusion that it is not practical to solve the FSI problem for onset of riprap motion with either software system by itself. Therefore, the primary objectives of numerical modeling tool development for this project were as follows:
After development of the tools, they were tested by application to a case study of riprap at a bridge pier in the Middle Fork Feather River described in chapter 5. The following section describes validation of the methodology.
The coupled FSI modeling tools were validated against the physical modeling described in chapter 3. After validating the numerical modeling tools against the flume modeling data, the results of the physical experiments were scaled up using Reynolds number similarity to evaluate the modeling with full-scale geometry.
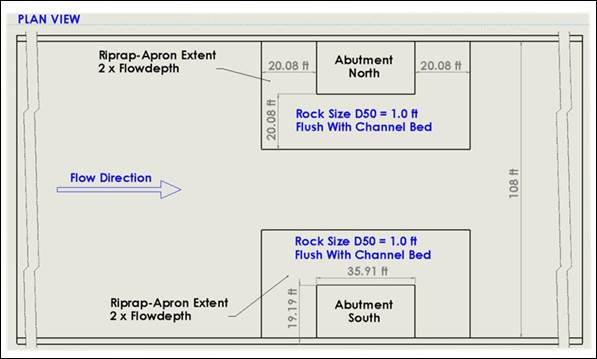
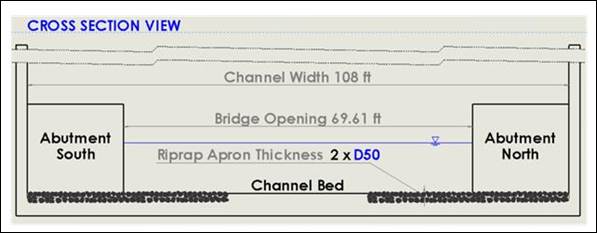
The numerical model geometry was derived from scaling up the experimental flume setup by a factor of 18. Figure 13 shows the plan view of the domain prototype dimensions including the rectangular channel, abutments forming the contracted section, and the riprap aprons intended to protect against local abutment scour. In the numerical analysis, only a half of this symmetrical domain was modeled to reduce the computational burden. Figure 14 shows the domain in a cross-section view.
1 ft = 0.305 m
Figure 13. Sketch. Plan view prototype domain.
1 ft = 0.305 m
Figure 14. Sketch. Cross-section view of the prototype domain.
One challenge for the numerical model was to determine the appropriate level of detail for the description of the rocks in the riprap apron, including randomized size, shape, and placement. To address this challenge, a limited number of rocks were allowed to move with the majority being fixed in the modeling. The implementation of the coupling mechanism described in appendix B requires the user to define many settings for each movable rock in STAR-CCM+, as well as in the LS-DYNA model. This process cannot be automated and is very time consuming.
Also, the structural part of the coupling relies on simulation restart capabilities in LS-DYNA that consume a significant amount of computer memory and time. The more movable rocks there are in the model, the longer it takes to restart the LS-DYNA model in each coupling time step. This is one of the limits of the coupling mechanism. These coupling limits, along with the domain remeshing in CFD, are the most time consuming elements of the computation.
For these reasons, the number of movable rocks was limited to 30. The fine mesh following all feature curves on the rocks were retained only for the movable rocks. The mesh in the CFD model around the movable rocks is very dense but coarsens farther away from them. Approximately 3,000 stationary rocks were manually placed in the testing area. Their packing was not as dense and random as in reality because of computational limitations.
After placing the rocks, the domain was wrapped with the surface wrapper before building the volume mesh. Wrapping the surface closed many small gaps and eliminated problems with intersecting boundaries. The edge size of the largest cells around the rocks distant from the movable ones was around 2.95 inches (75 mm), while the smallest edges sizes near to the movable rocks were less than 0.2 inches (5 mm). The resulting CFD model shown in figure 15 contains 4.4 million polyhedral cells.
The movable rocks were placed sparsely in the same failure location described for the physical experiments. All 30 movable rocks had the same shape, but their orientation was randomized. The movable rocks are shown in figure 15 as darker in both middle panel and lower panels of the figure.
 |
| A. Broad perspective. |
 |
| B. Medium perspective. |
 |
| C. Close perspective. |
Figure 15. Graphics. Rock layout in the CFD model.
Within LS-DYNA, the placement of the movable rocks could not be performed manually. Equilibrium positions for each rock were determined in a finite element simulation so that they had proper contact with the ground and would not shift only from the application of gravitational forces. The LS-DYNA model included 1.3 million shell elements and 30 inertia elements attached to the center of gravity of the movable rocks. The stationary bed was constructed from the wrapped surface from STAR-CCM+. Explicit time integration was used with a time step of 4.50E-06 s. The rock drop simulation was run for 10 s of real time. That procedure took approximately 7 h on 64 cores of the TRACC Zephyr cluster. The initial positions of movable rocks as well as their final equilibrium positions are shown in figure 16.
 |
| A. Pre-drop. |
 |
| B. Final. |
Figure 16. Graphics. Positions of movable rocks.
The surfaces describing the final position of the movable rocks were extracted from LS-DYNA and imported to the STAR-CCM+ model. The shell elements used for movable rocks in LS-DYNA represent a zero thickness surface, but actually have a thickness of 0.039 inches (1mm). The contact definition in LS-DYNA does not allow for penetrations of the movable rocks into the bed, which results in at least a 0.039 inch (1 mm) gap between the rocks and the bed in STAR-CCM+ model. This definition is required to prevent computational instabilities resulting from squeezing the computational cells to zero thickness in the case of contacts or collisions between movable rocks and the bed.
The force resulting from gravity is important for modelling rivers and other fluids with free surfaces. Therefore, the major governing non-dimensional parameter for model/prototype scaling is the Froude number. Flow conditions in the prototype-scale CFD simulations were calculated based on the Froude similarity with the experimental conditions. The approach flow depth was 10.0 ft (3.06 m) and the D50 was 12 inches (306 mm). The prototype range of velocities from the physical experiments described in chapter 3 ranged from 3.76 to 6.11 ft/s (1.145 to 1.87 m/s). The CFD analyses were performed on a subset of these inlet velocities—3.76, 4.27, 4.59, 4.92, 5.25, and 5.58 ft/s (1.145, 1.3, 1.4, 1.5, 1.6, and 1.7 m/s)—to create initial states for the FSI analyses. This subset was needed to identify the conditions of initial rock motion in the FSI analyses. The inlet velocity was assumed constant across the inlet boundary.
To simplify the analyses, the two-phase nature of open channel flow (water and air) was disregarded and only the water phase was simulated using a “closed-lid” representation. The closed-lid approach was chosen over the more realistic two-phase volume of fluid (VOF) approach because it is significantly less computationally intensive and more robust. The closed-lid assumption forces a constant water height in the model and uses a symmetry boundary condition at the water surface. The disadvantage of the closed-lid approach is that in reality the water level would drop slightly in the contraction zone and rise upstream of the contraction. Therefore, the numerical modeling with a closed-lid would indicate a smaller contraction flow area in the upstream portion of the contraction and upstream of the contraction than would be observed in the physical experiments. In this part of the domain, the closed-lid approach was considered to be conservative because the average velocity in the numerical model would be higher than in the physical model, causing rocks to be set in motion at a slightly, lower-approach water velocity. Once the lower contraction depth is fully established, the closed-lid approach would be result in an over-estimate of velocity and not provide a conservative estimate. These differences were assumed to be minor.
A time step of 0.025 s was used in the unsteady Reynolds-Averaged Navier-Stokes (RANS) solver for the CFD and the FSI modeling. The standard k-epsilon turbulence model was used in the analyses.
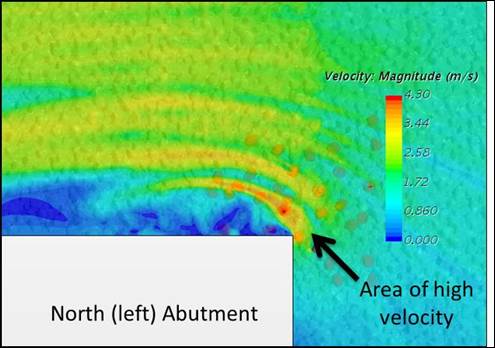
The CFD analysis with an inlet velocity of 4.27 ft/s (1.3 m/s) was identified as the threshold velocity for which failure of riprap was detected. Figure 17 shows a velocity distribution just above the riprap rocks from that simulation. Although the average velocity in the contraction zone is approximately 8.2 ft/s (2.5 m/s), the local water velocity can be as high as 14.1ft/s (4.3 m/s) near the corner of the abutment.
Figure 18 shows a perspective view of the abutment at the end of the CFD simulation. The pressure was overlaid on the surface of the movable rocks. The ten rocks experiencing the highest pressures are identified in the figure. All are located by the inlet to the contraction zone where the flow acceleration occurs. Both pressure and shear forces were included in the analysis, however, the pressure components are significantly higher than shear by two to three orders of magnitude.
1 ft/s = 0.305 m/s
Figure 17. Graphic. Velocity profile in a horizontal slice just above the riprap rocks with an inlet velocity of 4.27 ft/s (1.3 m/s).

1 lbf/ft2 = 47.88 Pa
Figure 18. Graphic. Location of the rocks with the highest forces in a CFD analysis.
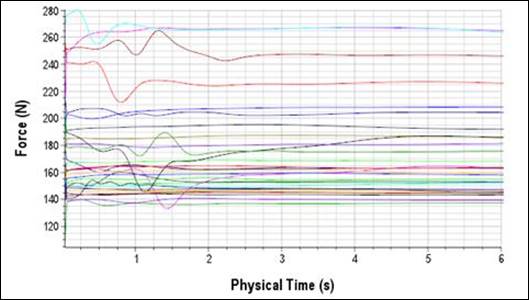
Figure 19 shows a representative example of force time histories in the Z-direction (vertical) for several individual rocks with an inlet velocity of 4.27 ft/s (1.3 m/s). Analogous force time histories were also available for the X-direction (flow direction). Forces in the Y-direction were not reported as they are significantly smaller than forces in the X- and Z-directions. As can be seen in figure 19, the forces were initially unstable but stabilized within approximately 5 s of simulated time.
1 lbf = 4.45 N
Figure 19. Graph. Initial stabilization of vertical forces on movable rocks.
To ensure consistency between the time series of the CFD and CSM analyses, the CFD runs were terminated at 5 s after the instabilities were resolved and the CFD time step was reset to zero retaining all state variables at the stabilized condition. This termination allowed a consistent specification of time equal zero between the two modeling components. The retained state variables from CFD were then imported to the CSM for time equals zero. In this way, both the CFD and CSM analyses were initialized consistently for the FSI analyses.
The primary forces acting on each individual rock are the drag, net weight (weight minus buoyancy), and contact forces. Net weight acts in the vertical direction. However, the direction of the drag force depends on the surrounding flow field; the direction of the contact forces depends on the orientation of neighboring rocks and the locations of their points of contact. Table 2 summarizes the X and Z forces at the end of the simulation, as well as the total resultant force, on the ten identified rocks. The rocks closest to the leading corner of the abutment (5 and 16) experienced the highest forces. Figure 20 illustrates the definition of the coordinate directions and the resultant force on an individual rock.
Movement of an individual rock will depend on the resultant force (including its direction), the weight of the rock (354 N), and the positioning of the movable rock with respect to the other rocks. The Z component of the force is larger than the X component in all cases. The Z component results from the weight and buoyancy as well as from the drag from significant flow in the voids between the stationary rocks. Recall that the packing density of the rocks results in greater void volumes than occurs in the physical experiments. In addition, the rocks away from the movable rocks are smoothed because of the larger cell sizes. Therefore, the Z forces are likely overestimated, which represents a conservative simplification of the model.
Table 2. Forces on ten movable rocks with varying inlet velocities.
| Rock No. |
Inlet Velocity 4.27 ft/s (1.3 m/s) | Inlet Velocity 4.59 ft/s (1.4 m/s) | Inlet Velocity 4.92 ft/s (1.5 m/s) | ||
|---|---|---|---|---|---|
| Z Force (N) | X Force (N) | Resultant (N) | Resultant (N) | Resultant (N) | |
| 16 | 262 | 145 | 299 | 330 | 370 |
| 5 | 264 | 122 | 291 | 319 | 352 |
| 21 | 246 | 86 | 261 | 282 | 306 |
| 15 | 225 | 46 | 230 | 257 | 279 |
| 6 | 208 | 36 | 211 | 222 | 237 |
| 23 | 204 | 45 | 208 | 221 | 237 |
| 26 | 181 | 95 | 204 | 220 | 234 |
| 20 | 185 | 78 | 200 | 210 | 236 |
| 12 | 186 | 59 | 195 | 205 | 217 |
| 9 | 191 | 37 | 194 | 202 | 220 |
| 1 lbf = 4.45 N | |||||
By accounting for the collisions and contacts between all rocks, the FSI modeling determines rock movements. The FSI simulations were performed with a coupling time step of 0.025 s, which was also the time step in the CFD modeling. The time step in LS-DYNA of 4.50E-06 s was significantly smaller to account for the collisions and contacts between the movable and stationary rocks. For each time step in STAR-CCM+, there were approximately 5,550 time steps in LS-DYNA. Ideally, these steps should be either equal to or inner iterations within one time step to achieve better accuracy. However, if 5 inner iterations within a time step are needed, then the overall computation time increases 5 times. For these validation studies, each simulation took approximately one week of computation time. This time is a reasonable duration for production runs. The assumed approach is believed to be a good compromise between the accuracy, efficiency, and the conservatism of the results.
Figure 21 shows several snapshots from the FSI simulation for the case with an inlet velocity of 4.27 ft/s (1.3 m/s). Three rocks with the highest forces on them are labeled. Rock 5 is positioned near the abutment corner and it is not moving in the FSI simulation at all. The other rocks experience a sudden push when they are “allowed” to move at the beginning of the FSI simulations. That causes them to oscillate, but they eventually return to their initial positions adjusted for the hydrodynamic forces introduced in the FSI.
Forces on the same ten movable rocks at inlet velocities of 4.59 ft/s (1.4 m/s) and 4.92 ft/s (1.5 m/s) at the end of the stationary CFD simulation are also summarized in table 2. For the inlet velocity of 4.59 ft/s (1.4 m/s), the order of forces is the same as for the lower velocity, but increase between 3 and 10 percent. At this velocity in the FSI analysis, more rocks leave their initial positions. Figure 22 shows several snapshots from the FSI simulation for that case. Rocks 9, 15, 16 and 23 exhibited the most noticeable movement. Several other rocks in the vicinity oscillated in position. Collisions of the rolling rocks with surrounding rocks triggered local motion of several more rocks. This inlet velocity was considered to be the threshold between stable and failing riprap.
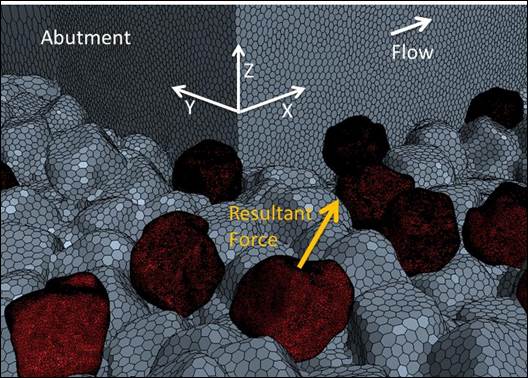
Figure 20. Graphic. Definition of forces on a single rock.
In the case with an inlet velocity of 4.92 ft/s (1.5 m/s) riprap failure became more apparent. The resultant forces increased approximately 10 percent over the previous inlet velocity condition. Figure 23 shows snapshots from that simulation. The rocks with most noticeable motions (9, 15, 16, 18, 23, 26) are labeled in this figure. In addition, rocks 6, 12, 18, and 20 become quite unstable and move locally.
Table 3 compares scaled results from the experiments with the results from the simulations. Scaling up the physical experiments to the prototype scale, the physical experiments validated that the riprap should be stable at an inlet velocity of 3.76 ft/s (1.145 m/s). Similarly, in the CFD simulation at this inlet velocity the rocks do not move from their initial positions. In the physical experiments, the threshold of rock displacement occurred at approximately 5.41 ft/s (1.65 m/s). In the numerical simulations, the threshold was judged to be at approximately 4.27 ft/s (1.3 m/s), approximately 21 percent lower. These results suggest that the numerical simulations are conservative, but are a reasonable representation of the physical behavior. It is hypothesized that the differences between the physical experiments and numerical simulations can be further decreased by more detailed mapping of the stationary rocks in the numerical simulations.
 |
 |
| A. 0.5 seconds. | B. 1.0 seconds. |
 |
 |
| C. 1.5 seconds. | D. 2.0 seconds. |
Figure 21. Graphics. FSI simulation for an inlet velocity of 4.27 ft/s (1.3 m/s).
 |
 |
| A. 0.5 seconds. | B. 1.0 seconds. |
 |
 |
| C. 1.5 seconds. | D. 2.0 seconds. |
Figure 22. Graphics. FSI simulation for an inlet velocity of 4.59 ft/s (1.4 m/s).
 |
 |
| A. 0.5 seconds. | B. 1.0 seconds. |
 |
 |
| C. 1.5 seconds. | D. 2.0 seconds. |
Figure 23. Graphics. FSI simulation for an inlet velocity of 4.92 ft/s (1.5 m/s).
Table 3. Comparison of physical experiments and computational simulations.
| Physical Experiments Scaled to Prototype | CFD/FSI Prototype Simulations | ||
|---|---|---|---|
| Upstream Velocity, ft/s (m/s) |
Observation from Physical Experiment |
Upstream Velocity, ft/s (m/s) |
Observation from Simulation |
| 3.76 (1.145) | Rocks stable, design velocity | 3.76 (1.145) | Rocks stable |
| 5.41 (1.65) | Upper limit where some rocks shaking, but no entrainment | 4.27 (1.3) | Potential instability of riprap |
| 5.84 (1.78) | Shear failure, rocks moved | 4.27 (1.3) | Potential riprap failure |
| 6.11 (1.87) | 4.59 (1.4) | ||