U.S. Department of Transportation
Federal Highway Administration
1200 New Jersey Avenue, SE
Washington, DC 20590
202-366-4000
Federal Highway Administration Research and Technology
Coordinating, Developing, and Delivering Highway Transportation Innovations
| REPORT |
| This report is an archived publication and may contain dated technical, contact, and link information |
|
| Publication Number: FHWA-HRT-13-066 Date: August 2013 |
Publication Number: FHWA-HRT-13-066 Date: August 2013 |
The Federal Highway Administration (FHWA) has developed a standard test method to describe the load-deformation behavior of a frictionally connected geosynthetic reinforced soil (GRS) composite material which can be used to predict performance of a GRS abutment.(1) The GRS performance test (PT), also called a mini-pier experiment, consists of constructing alternating layers of compacted granular fill and geosynthetic reinforcement with a facing element that is frictionally connected, then axially loading the GRS mass while measuring deformation to monitor performance. This large element load test provides material strength properties of a particular GRS composite built with different combinations of reinforcement, compacted fill, and facing elements. This report describes the procedure and provides axial load versus deformation results for a series of PTs conducted in both Defiance County, OH, as part of the FHWA's Every Day Counts (EDC) GRS Validation Sessions and in McLean, VA, at the FHWA's Turner- Fairbank Highway Research Center (TFHRC) as part of a parametric study.
The FHWA first demonstrated the concept of a mini-pier experiment in 2000 with the “Vegas Mini-Pier” experiment, shown in figure 1.(1,2) The pier was 8 ft tall with square inside dimensions of 3.5 ft, which represents a height (H) to base width (B) ratio of 2 (figure 2 through figure 4). This H/B ratio is consistent with typical triaxial testing for soils. (3)

Figure 1 Photo.Vegas mini-pier experiment.
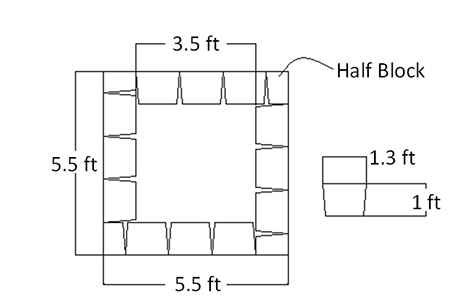
Figure 2. Illustration. Plan view of Vegas mini-pier experiment.
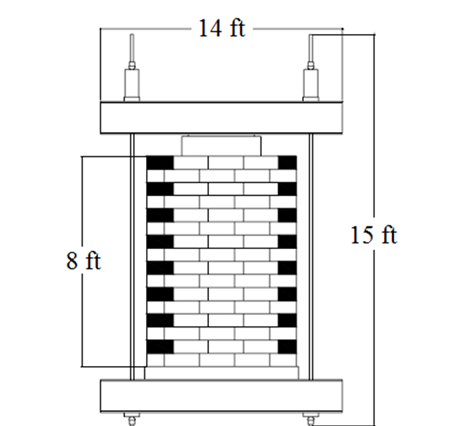
Figure 3. Illustration. Face view of Vegas mini-pier experiment.
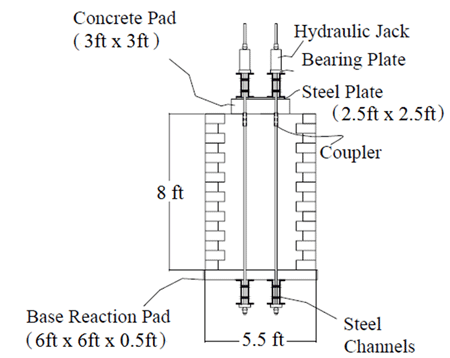
Figure 4. Illusration. Side view of Vegas mini-pier experiment.
The materials used for the GRS pier were a poorly graded-silty gravel (GP-GM, according to the Unified Soil Classification System, or USCS) soil with a 2,400 lb/ft (ultimate wide width tensile strength) geotextile spaced every 6 inches frictionally connected to segmental retaining wall (SRW) blocks for the facing. The top two courses of block, 1 ft from the top of the mini-pier, had two intermediate bearing bed reinforcement layers as shown in figure 5. The resulting pier was loaded up to 146 psi; however, time constraints and stroke limitations for the jacks prevented loading to failure of the composite. Since then, several additional performance tests have been completed, with the largest load carrying capacity reported at 176 psi. (4,5)
The concept of testing GRS material has been previously applied on smaller scale models ranging from small triaxial sized samples to 2-ft cubed specimens in smaller capacity test frames. (6,7) Several large scale tests have also been conducted.(7,8,9) For the aggregates recommended by FHWA for bridge support, large scale tests are required to adequately predict performance of a full-scale GRS abutment.(1) The proposed FHWA PT has been shown to accurately predict both the strength limit and the service limit for GRS abutments. (5)
To investigate GRS material further, the FHWA conducted a series of 19 PTs as part of this research. The layout for these PTs was a slight modification of the Vegas Mini-Pier experiment. Since these tests were conducted with concrete masonry units (CMU) for the facing, as opposed to SRW blocks used in the Vegas PT, different test dimensions were needed to retain the H/B ratio of 2 throughout testing. For CMUs, the typical performance test is 6.4 ft tall with square inside dimensions of 3.2 ft (figure 6 and figure 7). The parameters that varied among tests were reinforcement spacing (from 4 to 16 inches), geotextile strength (from 1,400 to 4,800 lb/ft, soil type (open-graded and well-graded), and frictionally connected facing element (concrete masonry unit facing and no facing).
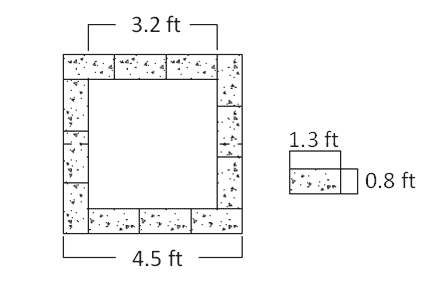
Figure 6. Illustration. Plan view of Defiance County experiment.
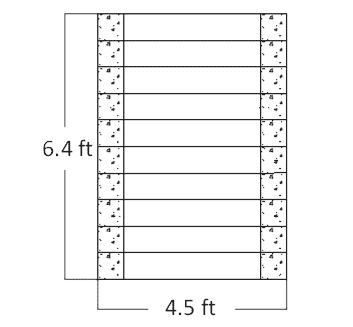
Figure 7. Illustration. Elevation view of Defiance County (DC) test.
The results of the PT are primarily used in the design of GRS abutments.(1) The resulting stress-strain curve can be used to describe the strength limit state for capacity and the service limit state for deformation (vertical and lateral) due to an applied load. It is the only method currently available to describe both the capacity and deformation behavior of GRS for load bearing applications; American Association of State Highway and Transportation Officials (AASHTO) (2012) does not provide any guidance for these GRS limit states. (10)
In addition to the empirically based design using PT results, a semi-empirical method is also presented by FHWA for internal stability design of GRS abutments and integrated bridge systems, based on basic soil mechanics principles for the relationship between vertical and lateral stress but is fit to the available data at the time. (1) The ultimate capacity is determined according to the equation presented in figure 8.(11) Note that in design, the effect of confining stress (due to the facing element) and cohesion is ignored, which for a CMU facing and the select granular fill specified for GRS abutments is an appropriate assumption.(5)
Where qult,an,c is the ultimate capacity using semi-empirical theory, σc is the external confining stress due to the facing, W is a factor accounting for the effect of reinforcement spacing and aggregate size (figure 9), Tf is the minimum average roll value (MARV) for wide width tensile strength of the geosynthetic, Kpr is the coefficient of passive earth pressure for the backfill, and c is the cohesion of the backfill.
Where Sv is the reinforcement spacing and dmax is the maximum aggregate size. The constant of 0.7 in the W-factor is the ratio of average force in the reinforcement to the maximum force in the reinforcement and the 6dmax term is an approximation of the minimum distance between reinforcement layers where the grain size of the soil will not significantly impact the composite behavior of the GRS. (12)
A variant of figure 8 is also used to determine the required reinforcement strength at a given applied stress (figure 10). The method provides engineers with the minimum strength of reinforcement needed to prevent failure of the GRS composite at that given applied stress. Note that figure 10 will not represent the actual load on the reinforcement at working stress once increased reinforcement strengths are used in the field since this will change the conditions. The actual load on the reinforcement is difficult to estimate; instead, the service limit for the reinforcement is based on limiting reinforcement strain to 2 percent.(1)
Where Treq,c is the required reinforcement strength in the direction perpendicular to the wall face, σh is the total lateral stress within the GRS composite at a given depth and location, is the external confining stress due to the facing, σc is the cohesion of the reinforced backfill, Kar is the coefficient of active earth pressure for the backfill, W is a factor accounting for the effect of reinforcement spacing and aggregate size (figure 9), and Sv is the reinforcement spacing. As with the ultimate capacity equation, the effect of confining stress (due to the facing element) and cohesion is ignored when determining the required reinforcement strength in the design of GRS abutments, leading to added conservatism in the design method.(5)
The soil-geosynthetic composite capacity equation (figure 8) and the required reinforcement strength equation (figure 10) have been previously validated against the results of 16 different types of tests, including previous performance tests (figure 12 and figure 13, respectively). The research study presented in this report will add to this database to further quantify the predictive capability of these equations.
Note that the predictions for capacity and required reinforcement strength used the estimated confining stress calculated according to figure 11, and the measured cohesion from soil testing, both of which would be ignored in design. In addition, the minimum average roll value (MARV) for the reinforcement, which is a property value calculated as the average strength for a roll less two standard deviations, was used to calibrate the predictive equations since the actual strength of the reinforcement for each test was not measured or precisely known, and the MARV is an industry value common for all geosynthetics specified in practice.
Where γb is the bulk unit weight of the facing block, d is the depth of the facing block unit perpendicular to the wall face, and δ is the interface friction angle between the geosynthetic and the facing element for a frictionally connected GRS composite.
Note that the friction angle and cohesion terms used to calculate the earth pressure coefficients and lateral stress within the ultimate capacity (figure 8) and required reinforcement strength (figure 10) equations were measured using a large scale direct shear (LSDS) test on the backfill alone according to ASTM D3080. (13) The peak strength of the reinforced backfill material was selected as it is a commonly reported value and easiest to ascertain from typical testing. More details are provided in section 2.1.3.
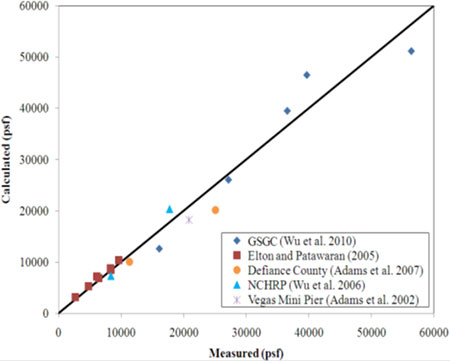
Figure 12. Graph. Predictive capability of the soil-geosynthetic composite capacity equation. (5)
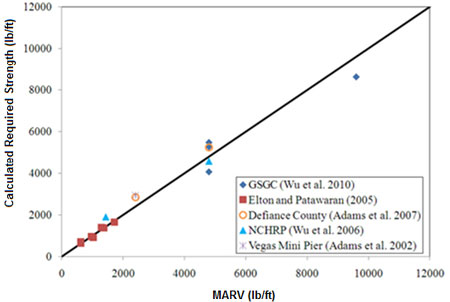
Figure 13 Graph. Predictive capability of the required reinforcement strength equation. (5)
The results of the PT parametric study will be used for several purposes. The primary objectives of this research report are to: (1) build a database of GRS material properties that can be used by designers or for Load and Resistance Factor Design (LRFD) calibration; (2) evaluate the relationship between reinforcement strength and spacing; (3) quantify the contribution of the frictionally connected facing elements at the service limit and strength limit states; (4) assess the new internal stability design method proposed by Adams et al. 2011a for GRS; and (5) perform a reliability analysis of the proposed soil-geosynthetic capacity equation for LRFD.(1,11) When combining additional measurement techniques (e.g., contact pressure cells, earth pressure cells, etc.), other uses for the PT are possible, such as to study thrust against the face as a function of spacing; however, this is outside the scope of this report.